Ishibuchi的经典的闭集框架下的模糊规则多类别分类器, 具有下面形式的if-then模糊规则。

Rule R_j: If x_i1 is A_j1 and … x_in is A_jn; Then Class D_j with CF_j, j=1, 2, …, N_rule(1)

式(1)中, N_rule是全部的模糊规则数量; 训练样本为x_i=(x_i1, x_i2, …, x_in), i=1, 2, …, N_train (N_train表示训练集中的样本数量); A_j1, …, A_jn是相应的模糊集, 分别对应于x_i1, …, x_in; D_j是该规则产生的结果类别(它是N_class个已知类别中的一个类别, 即D_j=C_i, i=1, 2, …, N_class); CF_j是模糊规则R_j的置信度。

在简化的1-vs-1二元分类器情况下, 对于每一个二元分类器, 上面的D_j只能是N_class个已知类别中的某两个类别。 因此总共需要设计和训练$C_{N_{\text {class}~~~}}^{2}$个1-vs-1二元分类器, 具体的训练过程类似于文献[16, 17, 18]的有关章节, 也类似于文献[15]的第2节, 限于篇幅这里不再赘述。

此外, 这里特别需要指出, 由于每个1-vs-1二元分类器只是分类处理两个类别, 因此相应的隶属度函数设计就比较简单了。 一般来说, 隶属度函数设计有3种方法。 第一种是等分布模糊化, 它根据经验选择的词数将话语域等分划分为若干部分。 第二种是自适应模糊化, 需要专家手动调整隶属度函数的数量和位置。 第三种是自动模糊化^[19]。 本工作采用第二种方法, 并通过以下4个步骤来完成模糊设置; 针对每一个1-vs-1二元分类器, 这4个步骤通常要执行几次。

(1) 使用Excel将数据均分为若干个区间, 并且计算数据在各个区间的频数, 得到数据在各个特征分量上的分布, 从而产生初始模糊的三角隶属度函数。

(2) 利用训练数据集执行模糊规则训练过程, 生成模糊规则集Q。

(3) 利用CF_j阈值找出严重冲突的模糊规则。

(4) 对这些冲突模糊规则, 得到它们在各个特征分量上的数据分布, 选择一个最适合下一轮划分的模糊集。

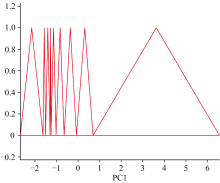
例如, 图1给出了某一个1-vs-1二元分类器的PC1特征分量上的隶属度函数优化设计结果, 该二元分类器分类处理的两个木材树种拉丁文名称为Ulmus glabra和Magnolia fordiana, 可以看出图1中有9个三角隶属度函数。 在这些三角隶属度函数中, 大部分是用来分类识别这两个已知的木材树种; 少部分是用来“ 拒识” 其他木材树种样本。 作为对比, 文献[15]的图5也给出了第一个特征分量上的隶属度函数优化设计结果, 它具有26个三角隶属度函数(训练集中包括10个已知树种), 远远超过了本文图1中第一个特征分量上的隶属度函数数量(训练集中包括两个已知树种)。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 某一个1-vs-1二元分类器的PC1的隶属度函数最终设计结果Fig.1 The final designed membership functions for PC1 of one 1-vs-1 binary classifier

在测试样本的分类处理阶段, 某一个测试样本x=(x₁, …, x_n)送入到$C_{N_{\text {class}~~~}}^{2}$个1-vs-1二元分类器进行分类处理。 对于每一个二元分类器BC_i(i=1, 2, …, $C_{N_{\text {class}~~~}}^{2}$), 执行下面的4个步骤。

(1) 对于每一个BC_i训练后生成的模糊规则集Q_i(i=1, 2, …, $C_{N_{\text {class}~~~}}^{2}$), 找到一些模糊规则R_j(j=1, 2, …, Nix), 它们的μ _j(x)· CF_j乘积值不为零。 这些模糊规则R_j称之为“ 非零” 模糊规则, 它们的数量 Nix与测试样本x以及模糊规则集Q_i有关。 这里的μ _j(x)需要事先做规一化, 它是测试样本x在模糊规则R_j中的隶属度函数值乘积, μ _j(x)=μ _j1(x₁)× …× μ _jn(x_n)。

(2) 在这些“ 非零” 模糊规则中, 如果有少量的R_j不包含于模糊规则集Q_i中, 那么它们的CF_j设置为1, 也即CF_j=1。

(3) 将这些“ 非零” 模糊规则分成3类, 前两类模糊规则的结果类别D_j分别是该BC_i的两个已知类别; 第三类模糊规则不包含于模糊规则集Q_i中(它们的CF_j=1), 对应于未知类别。 针对这3类模糊规则, 分别计算出3个求和 ∑μj(x)·CFj。

(4) 如果这3个求和中的最大值 max∑μjx·CFj对应于未知类别, 那么该测试样本 x=x1, …, xn无法被该 BCi识别, 从而测试样本 x得到零票。否则, 该最大值对应于某个已知类别, 从而测试样本 x在该已知类别得到一票。

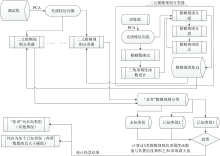
上述的4个步骤需要针对每个二元分类器BC_i(i=1, 2, …, $C_{N_{\text {class}~~~}}^{2}$)都执行一次, 然后, 统计测试样本x在各个已知类别中的得票数。 如果某个已知类别的得票数最高, 并且该最高得票数大于预先确定的阈值τ , 那么测试样本判决为该已知类别; 否则就“ 拒识” 为未知类别。 需要说明一点, 本工作中使用主成分分析法(principal component analysis, PCA)进行光谱向量的维度约简, 木材数据集选取前4个主成分作为光谱分类特征向量, 也即测试样本x=(x₁, …, x_n)=[PC1, PC2, PC3, PC4]; 芒果数据集选取前5个主成分作为分类特征向量[PC1, PC2, PC3, PC4, PC5]。图2给出了本文提出的基于模糊规则1-vs-1二元分类器组合的模糊分类流程图。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于模糊规则1-vs-1二元分类器组合的模糊多类别分类流程图Fig.2 Fuzzy multiclass classification flow chart based on combinations of fuzzy rule 1-vs-1 binary classifiers

采用了两类光谱数据集, 即木材树种的近红外光谱反射率数据集和芒果品种的光谱透射率数据集。 其中, 木材树种光谱数据集是利用本实验室自行搭建的光谱采集设备采集获取的。 使用的木材树种样本为2 cm× 2 cm× 3 cm 的小木块, 采用Flame-NIR微型近红外光谱仪采集木材样本横切面的光谱反射率曲线, 光谱波段为950~1 650 nm, 光谱分辨率为5.4 nm, 采集的光谱向量为128维(128D)。 每个树种包括50个木材样本, 因此采集了50条光谱曲线; 总共有25个木材树种, 具体的信息参见表1, 相应的光谱反射率曲线参见图3。 此外, 芒果品种光谱数据集来源于网络中的开源数据集^[20], 总共有10个品种, 分别是Caly, HG, Keitt, KP, LadyG, LadyJ, R2E2, 1 201, 1 243, 4 069。 这些芒果品种是培育的新品种, 没有正式的英文名称和拉丁文名称。 芒果品种光谱透射率曲线波段区间为285~1 200 nm, 光谱分辨率为3 nm, 光谱向量为306维(306D)。 每个芒果品种包括331条光谱曲线, 相应的光谱透射率曲线参见图4。

表1

Table 1

表1(Table 1)

表1 使用的木材树种数据集(25个木材树种) Table 1 The used wood species dataset with 25 species Class label Latin name 1 Pterocarpus soyauxii 2 Ulmus glabra 3 Calophyllum brasiliense 4 Intsia bijuga 5 Tectona grandis 6 Pouteria speciosa 7 Quercus mongolica 8 Magnolia fordiana 9 Guibourtia ehie 10 Terninalia catappa 11 Cinnamomum camphora 12 Guibourtia demeusei 13 Swintonia florbund 14 Fraxinus mandshurica 15 Pometia pinnata 16 Dipterocarpus alatus 17 Vernicia fordii 18 Sophora japonica 19 Robinia pseudoacacia 20 Quercus acutissima 21 Acer davidii 22 Amygdalus davidiana 23 Aucoumea klaineana 24 Betula alnoides 25 Betula platyphylla

表1 使用的木材树种数据集(25个木材树种) Table 1 The used wood species dataset with 25 species

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 25个木材树种的近红外光谱反射率曲线图 图中序号与表1编号一致, 表示木材树种名称Fig.3 Spectral reflectance curves of 25 wood species Serial number is the same as that in Table 1 which illustrates wood species)

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 10个芒果品种的光谱透射率曲线图 图中序号与前面所述的芒果品种名称顺序一致, 表示芒果品种名称Fig.4 Spectral transmissivity curves of 10 mango species Serial number is the same as that sequence mentioned above

为了进行这两类光谱数据集的开集分类识别实验, 需要把数据集划分为已知类别和未知类别。 对于木材光谱数据集, 设计了5组不同的划分, 每组划分具有不同的已知类别数和未知类别数, 具体信息参见表2。 上述的5组中, 已知类别样本都是以7∶ 3的比例划分为训练集和测试集, 未知类别样本全部用作测试样本。 例如, 第一组中3个类别作为已知类别进行模糊规则训练和生成, 22个类别作为未知类别。 对于已知类别以7∶ 3比例划分为训练集和测试集。 因此已知类别树种的测试样本数量为45, 未知类别树种的测试样本数量为1 100个, 比例为9∶ 220。 类似的, 对于芒果光谱数据集, 设计了2组不同的划分, 具体信息参见表3。

表2

Table 2

表2(Table 2)

表2 木材树种光谱数据集的分组 Table 2 Group division of wood spectral dataset Group division Known class number Unknown class number Known class sample number Unknown class sample number Known/unknown sample ratio Group 1 Training set 3 0 105 0 N/A Testing set 3 22 45 1 100 9∶ 220 Group 2 Training set 5 0 175 0 N/A Testing set 5 20 75 1 000 3∶ 40 Group 3 Training set 8 0 280 0 N/A Testing set 8 17 120 850 12∶ 85 Group 4 Training set 10 0 350 0 N/A Testing set 10 15 150 750 1∶ 5 Group 5 Training set 12 0 420 0 N/A Testing set 12 13 180 650 18∶ 65

表2 木材树种光谱数据集的分组 Table 2 Group division of wood spectral dataset

表3

Table 3

表3(Table 3)

表3 芒果品种光谱数据集的分组 Table 3 Group division of mango spectral dataset Group division Known class number Unknown class number Known class sample number Unknown class sample number Known/unknown sample ratio Group 1 Training set 3 0 695 0 N/A Testing set 3 7 298 2 317 9∶ 70 Group 2 Training set 5 0 1 159 0 N/A Testing set 5 5 496 1 655 3∶ 10

表3 芒果品种光谱数据集的分组 Table 3 Group division of mango spectral dataset

在本节中, 提出的方法将和其他的6种OSR方法做对比, 评价指标为Overall Recognition Accuracy (ORA), Kappa 系数以及F-Score。 针对2.1节中的分组, 本方法中1.2节涉及的阈值τ 分别是1、 3、 4、 5、 6(木材数据集5组); 1、 0(芒果数据集2组)。 第一种对比OSR方法是我们曾经提出的改进的Ishibuchi的模糊规则多类别OSR分类器, 它使用GBPA来构建各已知类别和未知类别的分类概率^[15]。 第二种对比OSR方法是Bendale和Boult提出的NNO分类算法^[5], 其分类阈值τ 分别是1.1、 0.8、 0.8、 0.8、 0.6(木材数据集5组); 1.0、 1.1(芒果数据集2组)。 这两种方法都是应用PCA进行光谱维度约简。

第三种对比OSR方法是加权支持向量数据描述(weighted support vector data description, Weighted-SVDD)组合LibSVM^[21], 分类过程有两步骤。 首先, 使用Weighted-SVDD进行单类分类, 将测试样本分类成已知类别和未知类别两大类; 参数值为σ =0.5, C=1.0(木材数据集)以及σ =2.0, C=1.5(芒果数据集)。 其次, 对于已知类别, 再使用LibSVM进一步细分为某个具体的物种类别; 参数值为σ =10, C=2.5(木材数据集)以及σ =5.0, C=1.0(芒果数据集)。 第四种对比OSR方法是Junior等提出的最近邻分类器的开集版本OSNN方法^[6], 分类阈值T_R=0.8(木材数据集)以及T_R=0.2(芒果数据集)。 这两种方法未做光谱维度约简。

第五种和第六种对比方法是扩展了经典的k最近邻分类器, 具体有3个步骤(这两种方法简称为k-nearest neighbor classifier, k-NNC算法)。 首先, 应用PCA进行光谱维度约简。 其次, 使用密度峰值聚类算法^[22]对于训练集中的各已知类别样本进行聚类。 第五种方法是通过聚类得到各已知类别的单个聚类中心; 第六种方法是通过聚类得到各已知类别的4个子聚类中心。 最后, 计算测试样本到训练集中的各已知类别的聚类中心或者子聚类中心的距离。 在第五种方法, 设求得的最近距离为d₁< T₁, 那么该测试样本判决为相应的已知类别; 否则就“ 拒识” 为未知类别。 在第六种方法, 设求得的最近距离为d₂< T₂, 同样做类似判决处理。 此处的距离阈值为T₁=0.2, T₂=0.1(木材数据集)以及T₁=0.4, T₂=0.2(芒果数据集), 通过网格搜索法求得优化后取值。 具体分类结果如表4—表10所示, 最佳评价指标以粗体表示; 表中给出了10次重复性实验的平均值和标准差。 在这些表中可以看出, 本方法在每组实验中均优于其他的OSR方法, 并且当已知类别数量增加时本方法的优势对比更加明显。

表4

Table 4

表4(Table 4)

表4 木材数据集第一组的分类性能对比 Table 4 Classification performance comparisons in group 1 of wood spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 98.57%± 0.01% 0.802 9± 0.008 7 0.807 3± 0.009 2 文献[15]方法 92.19%± 0.37% 0.458 9± 0.015 4 0.491 4± 0.017 2 NNO 64.57%± 7.59% 0.163 0± 0.014 5 0.130 5± 0.002 9 Weighted-SVDD/LibSVM 76.97%± 0.67% 0.224 6± 0.013 6 0.259 2± 0.012 2 OSNN 7.52%± 0.05% 0.014 0± 0.000 1 0.076 6± 0.000 1 k-NNC (1center) 96.01%± 0.01% 0.287 3± 0.020 0 0.297 7± 0.020 4 k-NNC (4center) 96.77%± 0.01% 0.387 0± 0.013 9 0.394 8± 0.013 9

表4 木材数据集第一组的分类性能对比 Table 4 Classification performance comparisons in group 1 of wood spectral dataset

表5

Table 5

表5(Table 5)

表5 木材数据集第二组的分类性能对比 Table 5 Classification performance comparisons in group 2 of wood spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 97.40%± 0.01% 0.769 5± 0.003 1 0.776 1± 0.003 4 文献[15]方法 93.00%± 0.36% 0.629 2± 0.014 0 0.664 4± 0.016 5 NNO 53.93%± 16.08% 0.200 7± 0.029 5 0.150 3± 0.006 4 Weighted-SVDD/LibSVM 53.22%± 0.91% 0.155 9± 0.001 3 0.216 8± 0.001 0 OSNN 13.80%± 0.09% 0.026 5± 0.000 1 0.124 7± 0.000 1 k-NNC (1center) 93.23%± 0.01% 0.330 5± 0.012 4 0.354 6± 0.012 1 k-NNC (4center) 94.55%± 0.01% 0.415 4± 0.008 5 0.427 4± 0.008 5

表5 木材数据集第二组的分类性能对比 Table 5 Classification performance comparisons in group 2 of wood spectral dataset

表6

Table 6

表6(Table 6)

表6 木材数据集第三组的分类性能对比 Table 6 Classification performance comparisons in group 3 of wood spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 97.84%± 0.01% 0.907 7± 0.001 8 0.913 1± 0.001 4 文献[15]方法 93.88%± 0.51% 0.772 1± 0.017 8 0.798 1± 0.014 6 NNO 23.16%± 3.65% 0.076 3± 0.002 7 0.121 0± 0.001 5 Weighted-SVDD/LibSVM 49.74%± 0.62% 0.224 9± 0.001 9 0.310 2± 0.001 3 OSNN 18.97%± 0.13% 0.035 6± 0.000 2 0.219 2± 0.000 5 k-NNC (1center) 89.48%± 0.02% 0.385 0± 0.003 0 0.417 0± 0.003 3 k-NNC (4center) 89.62%± 0.01% 0.343 0± 0.010 3 0.363 7± 0.010 6

表6 木材数据集第三组的分类性能对比 Table 6 Classification performance comparisons in group 3 of wood spectral dataset

表7

Table 7

表7(Table 7)

表7 木材数据集第四组的分类性能对比 Table 7 Classification performance comparisons in group 4 of wood spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 97.65%± 0.01% 0.924 1± 0.000 4 0.931 6± 0.000 3 文献[15]方法 93.47%± 0.35% 0.805 4± 0.008 4 0.838 9± 0.008 2 NNO 18.05%± 1.67% 0.085 1± 0.003 4 0.128 5± 0.001 0 Weighted-SVDD/LibSVM 55.57%± 0.55% 0.313 2± 0.003 5 0.405 1± 0.002 4 OSNN 23.25%± 0.01% 0.050 5± 0.000 1 0.298 4± 0.000 3 k-NNC (1center) 85.75%± 0.01% 0.369 0± 0.000 7 0.410 1± 0.001 0 k-NNC (4center) 85.88%± 0.01% 0.325 6± 0.005 3 0.353 6± 0.005 3

表7 木材数据集第四组的分类性能对比 Table 7 Classification performance comparisons in group 4 of wood spectral dataset

表8

Table 8

表8(Table 8)

表8 木材数据集第五组的分类性能对比 Table 8 Classification performance comparisons in group 5 of wood spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 97.19%± 0.01% 0.927 3± 0.000 1 0.937 3± 0.000 1 文献[15]方法 93.83%± 1.21% 0.845 3± 0.031 5 0.889 4± 0.011 2 NNO 28.15%± 0.96% 0.127 7± 0.002 4 0.149 1± 0.000 4 Weighted-SVDD/LibSVM 59.57%± 0.76% 0.402 2± 0.006 1 0.498 3± 0.003 8 OSNN 23.59%± 0.01% 0.054 9± 0.000 1 0.355 3± 0.000 1 k-NNC (1center) 81.33%± 0.01% 0.347 0± 0.000 2 0.399 9± 0.000 2 k-NNC (4center) 82.05%± 0.01% 0.326 3± 0.001 8 0.363 5± 0.001 7

表8 木材数据集第五组的分类性能对比 Table 8 Classification performance comparisons in group 5 of wood spectral dataset

表9

Table 9

表9(Table 9)

表9 芒果数据集第一组的分类性能对比 Table 9 Classification performance comparisons in group 1 of mango spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 94.31%± 0.01% 0.699 9± 0.006 1 0.756 2± 0.004 4 文献[15]方法 85.22%± 0.48% 0.494 3± 0.007 4 0.552 5± 0.007 2 NNO 74.34%± 2.14% 0.275 1± 0.019 4 0.028 9± 0.000 2 Weighted-SVDD/LibSVM 89.26%± 0.01% 0.114 0± 0.016 8 0.119 9± 0.019 0 OSNN 62.26%± 0.09% 0.098 9± 0.001 2 0.216 8± 0.000 6 k-NNC (1center) 90.30%± 0.01% 0.309 9± 0.000 4 0.324 2± 0.000 4 k-NNC (4center) 89.39%± 0.01% 0.237 8± 0.012 0 0.256 7± 0.012 9

表9 芒果数据集第一组的分类性能对比 Table 9 Classification performance comparisons in group 1 of mango spectral dataset

表10

Table 10

表10(Table 10)

表10 芒果数据集第二组的分类性能对比 Table 10 Classification performance comparisons in group 2 of mango spectral dataset OSR方法 评价指标 ORA Kappa系数 F-Score 本方法 87.89%± 0.01% 0.713 4± 0.000 1 0.849 5± 0.000 1 文献[15]方法 85.70%± 0.63% 0.664 1± 0.012 2 0.724 8± 0.009 2 NNO 70.69%± 0.13% 0.350 5± 0.001 9 0.060 3± 0.002 7 Weighted-SVDD/LibSVM 77.96%± 0.01% 0.096 3± 0.004 9 0.086 8± 0.008 4 OSNN 60.68%± 0.01% 0.095 5± 0.000 1 0.284 6± 0.000 1 k-NNC (1center) 79.64%± 0.01% 0.193 8± 0.000 1 0.215 1± 0.000 1 k-NNC (4center) 78.23%± 0.01% 0.143 3± 0.005 1 0.179 9± 0.005 7

表10 芒果数据集第二组的分类性能对比 Table 10 Classification performance comparisons in group 2 of mango spectral dataset

此外, 为了进一步说明本方法相对于其他OSR方法的分类处理优势, 还对于芒果数据集表9和表10的分类实验结果对比做了进一步的统计检验, 使用了双尾McNemar's Test^[23]。 需要说明一点, 由于木材数据集中每个树种只是采集了50条光谱曲线, 样本数量偏少, 无法做双尾McNemar's Test统计检验, 因此该统计检验只针对芒果数据集进行。 该统计检验结果参见表11, 表中的p< 0.05的时候, 表示相应的两种OSR方法具有统计意义的差异。 可以看出, 本方法相对于其他OSR方法来说, 具有统计检验意义的优势。

表11

Table 11

表11(Table 11)

表11 本方法对比其他OSR方法的双尾McNemar's Test统计检验p值 Table 11 The p value of dual tail McNemar's Statistical Test for our proposed scheme compared with other OSR schemes OSR方法 实验组 p(第一组) p(第二组) 文献[15]方法 < 0.000 001 0.031 826 NNO < 0.000 001 < 0.000 001 Weighted-SVDD/LibSVM < 0.000 001 < 0.000 001 OSNN < 0.000 001 < 0.000 001 k-NNC (1center) < 0.000 001 < 0.000 001 k-NNC (4center) < 0.000 001 < 0.000 001

表11 本方法对比其他OSR方法的双尾McNemar's Test统计检验p值 Table 11 The p value of dual tail McNemar's Statistical Test for our proposed scheme compared with other OSR schemes

从2.2节的实验结果对比可以看出, 本方法相对于其他OSR方法, 的确具有明显优势。 分析其原因, 我们总结了以下3点。 首先, 本文提出的模糊规则多类别分类OSR方法是基于每个二元模糊规则分类器BC_i(i=1, 2, …, $C_{N_{\text {class}~~~}}^{2}$), 每个BC_i只是分类处理1-vs-1的两个已知类别。 这样, 相应的各个特征分量上的隶属度函数设计就相对简单了, 并且训练生成的模糊规则集Q_i中发生模糊规则冲突的概率大大降低了, 这有利于后续的分类处理。 其次, 由于每个BC_i只是分类处理两个已知类别(分类处理的已知类别数量很少), 这就给未知类别预留了充足的模糊子空间, 这有利于“ 拒识” 未知类别样本, 从而保证OSR分类处理精度。 例如, 图5给出了某个二元模糊规则分类器的模糊子空间划分情况, 每个特征分量使用了6个均匀划分的三角隶属度函数, 这样就总共产生了36个模糊子空间(也即模糊规则)。 其中, 红色和绿色网格是分配给了两个已知类别, 剩下的蓝色网格分配给了未知类别。 可以看出, 在这些二维(2D)的模糊子空间中, 总共只有两个已知类别和一个未知类别, 分类处理相对简化了, 更容易“ 辨识” 已知类别和“ 拒识” 未知类别; 从而保证了分类识别精度。 最后, 使用1-vs-1二元模糊规则分类器组合进行多类别分类处理, 即使某些已知类别之间较难区分, 也可以通过其他二元分类器进行协助分类。 比如在12个已知类别和8个未知类别的情况下, 类4和类12之间较难区分, 我们可以通过类4-vs-类j(j=1, 2, 3, 5, …, 11)的二元分类器与类12-vs-类j(j=1, 2, 3, 5, …, 11)的二元分类器来协助分类处理类4和类12; 从而保证了类4和类12的分类处理精度。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 某个二元模糊规则分类器的2D模糊子空间划分Fig.5 2D fuzzy subspace division of one fuzzy rule binary classifier