采样地点位于中国海南省儋州市中国热带农业科学院橡胶研究所试验场三队(109° 28'E, 19° 32'N), 该地区的气候为热带季风气候, 年平均降雨量1 815.6 mm, 年平均气温23.2 ℃, 适宜的温度与充足的降雨量有利于PM的发生与传播。 使用的橡胶树品种编号为“ RY-7-33-97” 。 于2024年11月— 12月在试验场不同区域随机采集了不同病害程度556份橡胶树病害叶片作为样本。 参照Cheng等对PM的分级标准^[8], 并在植保专家的鉴定下, 在试验场将叶片根据其病情划分为六个不同的阶段, 具体划分规则如表1 所示。

表1

Table 1

表1(Table 1)

表1 叶片白粉病划分标准 Table 1 Standards for classification of leaf powdery mildew 病害等级 白粉病病斑面积占叶片面积的比例(X) 数量 0 X=0 74 1 0< X≤ 1/8 99 2 1/8≤ X< 1/4 94 3 1/4≤ X< 1/2 100 4 1/2≤ X< 3/4 98 5 3/4≤ X, 或叶片皱缩, 或叶片脱落 91 注: 叶片病斑双面重叠只计一面 Note: For leaf lesions overlappling on both two sides, only one side is counted.

表1 叶片白粉病划分标准 Table 1 Standards for classification of leaf powdery mildew

将标注好的叶片放入密封袋中, 送入实验室进行光谱测量。 使用GaiaField-F-N17E成像仪获取叶片样本的高光谱图像, 高光谱波段范围为866.4~1 701.0 nm, 间隔3.3 nm, 共包含254个波段, 去除信噪比较低的部分首尾波段后, 剩余214个波段用于病害分类。 为了降低亮度波动对数据的影响, 并增强光谱数据的精度与可信度, 在进行数据处理之前, 需要对高光谱数据执行黑白校准。 所采集的高光谱图像同时包括叶片和背景, 为了排除背景干扰, 将叶片的有效区域确定为感兴趣区域, 并将其作为掩膜将叶片像素与背景分离。 将去除背景后的每个样本图像中所有叶片像素的光谱反射率平均后得到单个叶片样本的平均光谱。

针对橡胶树叶片高光谱数据中的噪声干扰、 散射效应及微弱特征不明显等问题, 分别采用Savitzky-Golay平滑(SG平滑)、 标准正态变换(standard normal variate, SNV)、 FOD处理原始光谱数据。 SG平滑能够提高光谱数据的平滑性, 降低噪声干扰。 SNV可以减轻光谱数据中的散射效应。 FOD能够增强光谱中的微弱特征, 放大频谱信息。 采用Grü nwald-Letnikov(G-L)方法实现FOD, 其公式为

$D_{x}^{a} f(x) \approx h^{-a} \displaystyle\sum_{r=0}^{\left[\frac{x-x_{0}~}{h}~\right]}(-1) r\binom{\alpha}{r} f(x-r h)$(1)

式(1)中, α 为分数阶阶次, h为离散化的步长参数, 高光谱波段间隔3.3 nm, 将h设为3.3, r为离散化步数, x₀为导数计算起始点, x导数计算终点, x-x0h取整函数, αr为二项式系数, 其计算公式为

αr=Γ(α+1)Γ(r+1)Γ(α-r+1) =1, r=0α(α-1)…(α-r+1)r!, r> 0(2)

式(2)中, Γ (x)为Gamma函数。 当α 为正整数时, 式(1)转化为经典导数公式。 采用0.1为步长进行0~2阶的FOD处理。

叶片高光谱数据具有高冗余、 非线性关联、 含噪声干扰等特点, 为了对比TabPFN算法的加权特征能力, 探索了不同特征选择算法对模型性能提升的可能性, 分别采用最大相关性最小冗余(max-relevance and min-redundancy, mRMR)、 ReliefF、 Hilbert-Schmidt Independence Criterion Lasso (HSICLasso)、 主成分分析(principal component analysis, PCA)提取数据有效信息。 这些算法能适配橡胶树高光谱数据的高冗余、 非线性关联等特点, 且通过与无监督方法对比可凸显TabPFN的加权特征优势。

mRMR算法基于信息论框架, 通过互信息最大化特征与目标类别之间的相关性, 同时最小化特征之间的冗余性, 筛选出分类性能强的特征子集^[22]。 ReliefF采用样本空间分析策略, 通过样本的邻近性评估特征重要性, 比较同类和异类样本在特征上的差异, 加权计算各特征的区分能力^[23]。 HSICLasso是一种结合非线性相关性与稀疏约束的特征选择方法, 通过最大化特征与目标变量的希尔伯特-施密特独立性(HSIC)来评估非线性关联, 利用L1正则化实现特征稀疏化, 筛选出与分类目标高度相关的光谱特征子集^[24]。 PCA是一种用于光谱数据降维的特征提取方法, 通过正交变换将原始高维光谱数据投影到低维空间, 保留数据方差最大的主成分方向, 能够保留原始数据信息并降低数据维度。

选择支持向量机(support vector machine, SVM)、 RF、 MLP、 TabPFN四种模型对叶片病害等级进行分类, 使用网格搜索结合5折交叉验证确定SVM、 RF、 MLP三种模型的超参数, TabPFN采用其默认参数。 部分模型对光谱数据尺度变化敏感, 在数据输入到模型前还进行了Z-score标准化处理。

TabPFN是一种专为表格数据设计的小样本学习模型, 通过预训练捕捉表格数据的通用先验分布。 TabPFN的主要原理如图1所示: (a)利用结构因果模型(structural causal model, SCM)生成涵盖多样化因果结构的训练数据集, 包括各种特征与目标之间的关系, 并利用贝叶斯神经网络学习其概率分布。 该过程使模型获得表格数据的通用归纳偏置, 形成强大的迁移能力。 (b)模型通过两条并行的注意力路径处理输入数据, 针对PM光谱数据来说: 单样本特征间注意力能够计算波段间的相关性, 加权融合病害敏感特征; 不同样本之间的注意力能挖掘各类别的光谱模式, 增强小样本泛化性。 此设计使TabPFN仅需单次前向传播即可完成预测, 无需微调其参数。

图1

Fig.1

	Figure Option ViewDownloadNew Window
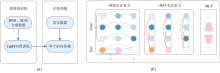	图1 TabPFN主要原理 (a): 模型拟合与推理; (b): 框架与注意力机制Fig.1 Main principle of TabPFN =(a): Model fitting and reasoning; (b): Framework and attention mechanism

为了评估模型的性能, 数据集按7: 3的比例随机划分为训练集和测试集, 且不设置随机种子。 每个实验独立运行10次, 并计算每次实验的准确率(Accuracy)、 精确率(Precision)和F1分数。 最终, 报告这些评价指标的平均值及标准差, 以反映模型在不同条件下的稳定性与表现。 三种指标的计算公式为

$\text { Accuracy }=\frac{~T P+T N}{~T P+F P+T N+F N~~~~} \times 100 \%$(3)

$\text { Precision }=\frac{T P}{~~T P+F P~~~} \times 100 \%$(4)

$\mathrm{~F} 1=\frac{2 \times T P}{~~2 \times T P+F P+F N~~~} \times 100 \%$(5)

式(3)— 式(5)中, 真阳性(TP)是模型正确预测正类的实例数, 真阴性(TN)是模型正确预测负类的实例数, 假阳性(FP)是模型错误预测正类的实例数, 假阴性(FN)是模型错误预测负类的实例数。 后续讨论中三种评价指标分别简称Acc、 Pre、 F1。

使用SHAP对模型可解释分析, SHAP是一种基于博弈论中Shapley值的模型可解释性方法, 通过量化每个特征对模型预测的边际贡献构建特征贡献度图谱, 其主要依据核心的加性法公式为

$f(x)=\Phi_{0}+\displaystyle\sum_{i=1}^{n} \Phi_{i}$(6)

式(6)中, f(x)是模型的评估结果, Φ ₀则是模型的平均预测值, Φ _i是特征i的SHAP值。 重复训练模型并计算SHAP值10次, 并对10次结果取平均, 从而获得更稳定的特征贡献度估计。

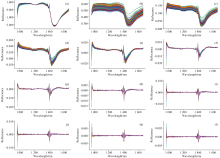
不同病害等级的叶片原始平均光谱如图2所示, 曲线在近红外区1 180~1 220和1 400~1 500 nm处出现明显吸收谷, 这与橡胶叶片内部水分子O— H键吸收光谱能量导致反射率降低相符合。 与患病叶片相比, 等级0的光谱整体反射率较低, 平均反射率低于0.55。 随着病害等级的提升, 叶片光谱特征出现分层, 等级为1、 2之间和3、 4之间的叶片谱线区间高度相似; 病害等级为5的叶片反射率相对最高, 整体反射率高于0.3, 且1 450 nm处的波动范围最大。 说明病害程度的增加会引起光谱曲线特征变化, 但相邻病害等级的光谱曲线存在接近性, 需借助算法分析进行精细区分。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 原始平均光谱曲线 (a): 类别0; (b): 类别1; (c): 类别2; (d): 类别3; (e): 类别4; (f): 类别5Fig.2 Original average spectral curves (a): Class 0; (b): Class 1; (c): Class 2; (d): Class 3; (e): Class 4; (f): Class 5

使用不同预处理算法对原始平均光谱曲线进行处理后得到的光谱曲线如图3所示。 经过SNV预处理后的光谱曲线如图3(a), 光谱曲线被缩放到同一尺度, 降低了散射效应对原始光谱数据的干扰。 应用SG平滑处理后的光谱曲线如图3(b), 光谱曲线的波动性减少并有效抑制了噪声。 图3(c)— (l)展示了以0.2为步长0.2~2阶分数阶处理下的光谱曲线, 可以看出, FOD阶数不断增加导致光谱曲线出现渐进变化, 大多数波段的反射率趋向0, 且在1 400 nm处出现明显的峰和谷。 说明FOD能改变光谱特征, 为后续的特征提取和建模分析提供了新的视角。

图3

Fig.3

Figure Option ViewDownloadNew Window

图3 不同预处理后的光谱曲线 (a): SNV; (b): SG平滑; (c): 0.2阶; (d): 0.4阶; (e): 0.6阶; (f): 0.8阶; (g): 1.0阶; (h): 1.2阶; (i): 1.4阶; (j): 1.6阶; (k): 1.8阶; (l): 2.0阶Fig.3 Spectral curves after different pretreatments (a): SNV; (b): SG smoothing; (c): 0.2 order FOD; (d): 0.4 order FOD; (e): 0.6 order FOD; (f): 0.8 order FOD; (g): 1.0 order FOD; (h): 1.2 order FOD; (i)1.4 order FOD; (j): 1.6 order FOD; (k): 1.8 order FOD; (l): 2.0 order FOD

为了评估FOD阶数对不同建模方法性能的影响并确定各方法在不同阶数下的最佳性能, 采用不同阶数的高光谱数据进行建模分析。 图4中展示了四种模型在不同特征阶数下的橡胶树PM病害分级性能变化规律。 实验结果表明TabPFN与SVM在全阶数范围内展现出较强的适应能力: TabPFN的准确率波动较小且始终高于0.91, 在1.2阶时达到峰值0.97; SVM在低阶区间(0.1~0.7阶)具有较高精度, 0.7阶时准确率达0.96, 但在高阶阶段出现性能衰减。 MLP和RF在低阶时准确率较低, 阶数的增加使其准确率逐渐提高并在高阶时趋于稳定。 MLP在高阶时表现更优, 在1.4阶后准确率与TabPFN和SVM相近。 RF在低阶阶段分类性能受限, 在1.3阶达到峰值0.86, 但其整体准确率始终低于其他模型。 实验数据表明, TabPFN和SVM适合特征阶数变化较大的场景, TabPFN表现出较强的鲁棒性, MLP和RF在较高的特征阶数能达到稳定性能。 MLP、 TabPFN、 RF、 SVM四种建模方法分别在1.5、 1.2、 1.3、 0.7阶时达到最佳分级能力, 后续对比实验中, 上述阶数将作为各模型的FOD的基准参数。

图4

Fig.4

	Figure Option ViewDownloadNew Window
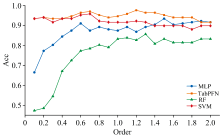	图4 不同FOD阶数的全特征下所有模型的建模准确率变化趋势Fig.4 The variation trend of modeling accuracy of all models with different FOD orders

全波段不同预处理方法下各模型在训练集和测试集上的预测结果如表2所示, 在未预处理(None)条件下, 模型对原始光谱的响应存在较大差异: SVM与TabPFN展现出较强的基线适应能力, 测试集F1分别为88.58%± 2.92%和90.50%± 2.40%; RF表现出严重的过拟合倾向, 训练集F1达98.73%± 0.29%而测试集骤降至52.76%± 4.43%, 反映原始特征空间中多重共线性对决策树集成的干扰; MLP同样存在过拟合问题, 测试集F1仅67.16%± 2.45%, 凸显深度模型对非线性关系的依赖。

表2

Table 2

表2(Table 2)

表2 不同预处理后的全特征下所有模型预测结果 Table 2 Prediction results of all models under full features after different pretreatments 预处理方法 建模方法 训练集 测试集 Acc Pre F1 Acc Pre F1 None SVM 96.14± 0.65 96.24± 0.65 96.22± 0.65 88.50± 2.81 88.96± 2.90 88.58± 2.92 RF 98.77± 0.30 98.72± 0.29 98.73± 0.29 53.05± 4.78 52.92± 4.11 52.76± 4.43 MLP 82.96± 3.70 83.54± 3.62 83.36± 3.62 66.59± 2.47 67.59± 2.65 67.16± 2.45 TabPFN 99.54± 0.41 99.56± 0.39 99.56± 0.39 90.30± 2.38 90.78± 2.30 90.50± 2.40 SG SVM 93.34± 0.92 93.47± 0.90 93.39± 0.92 84.79± 3.03 85.52± 3.09 84.87± 3.10 RF 99.05± 1.21 99.02± 1.23 99.04± 1.21 51.08± 3.05 51.45± 2.43 51.13± 2.70 MLP 81.98± 3.17 82.30± 3.29 82.32± 3.22 62.40± 3.64 63.60± 3.34 63.05± 3.36 TabPFN 97.84± 1.12 97.86± 1.08 97.88± 1.09 83.77± 3.45 84.91± 3.47 84.15± 3.41 SNV SVM 99.95± 0.15 99.95± 0.15 99.95± 0.15 89.16± 2.91 89.56± 2.95 89.34± 2.95 RF 100± 0 100± 0 100± 0 73.53± 3.45 74.22± 3.40 73.73± 3.37 MLP 100± 0 100± 0 100± 0 84.97± 2.90 85.42± 2.87 85.11± 2.90 TabPFN 100± 0 100± 0 100± 0 94.55± 1.09 94.82± 1.01 94.66± 1.05 FOD SVM 99.82± 0.23 99.82± 0.23 99.82± 0.23 92.28± 2.03 92.64± 1.88 92.43± 2.01 RF 100± 0 100± 0 100± 0 84.13± 2.20 84.57± 2.24 84.14± 2.28 MLP 100± 0 100± 0 100± 0 89.34± 2.84 89.63± 2.76 89.42± 2.79 TabPFN 100± 0 100± 0 100± 0 95.27± 1.21 95.46± 1.22 95.26± 1.21

表2 不同预处理后的全特征下所有模型预测结果 Table 2 Prediction results of all models under full features after different pretreatments

SG平滑处理虽部分抑制了光谱噪声, 却导致模型性能较None的普遍下降, 这表明平滑过程在消除噪声的同时, 也削弱了关键判别频段的特征表达能力。 SNV处理显著改善了模型的分类性能: RF与MLP的性能有较大提升, 但总体性能仍低于SVM、 TabPFN; SNV-TabPFN较None-TabPFN测试集F1提升4.60%; FOD处理则展现出全面优势, 所有模型测试集Acc、 Pre、 F1均值均突破84%, 且优于SNV处理下的模型性能。 其中FOD-TabPFN的Acc达到峰值95.27%, 较None-TabPFN提升5.26%, 标准差下降约49.58%, 数据离散程度大幅降低。 FOD处理下各模型训练集指标均接近100%, 测试集性能未出现明显衰减, 表明该方法通过微分阶数优化实现了判别特征的高效提取, 既保留了光谱细节又抑制了噪声。 该结果验证了分数阶微分在特征增强中的普适性, 优于其他三种预处理方法。 因此, 采用FOD作为标准预处理方法进行特征选择建模研究。

使用不同特征选择算法的筛选出的特征波段如图5所示, 三不同特征选择算法的筛选结果揭示了各自独特的特征波段分布规律: ReliefF算法选出的特征波段主要集中在1 170和1 400 nm附近, 呈现出明显的局部性; mRMR算法则筛选出了分布较为均匀的特征波段, 覆盖了1 000、 1 200和1 400~1 600 nm 区间, 显示出更广泛的特征选择趋势; HSICLasso算法的筛选结果最为广泛, 涉及从970到1 600 nm 的多个波段区间。 相关研究表明, 970 nm与叶片水分和淀粉含量密切相关; 1 200 nm波段与水分、 纤维素、 淀粉和木质素的含量有关; 而1 400~1 600 nm波段则涉及叶片水、 纤维素、 淀粉、 木质素、 蛋白质及氮素等成分^[25]。 这些结果表明, 三种算法展示了不同的特征选择策略, 为后续模型构建提供了多元化的特征支持。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同特征选择算法的筛选出的特征波段Fig.5 Feature bands selected by different selection algorithms

使用FOD结合不同特征选择算法的情况下, 各模型预测结果如表3所示。 由表可知, TabPFN算法表现最佳, 其全波段建模与特征选择建模的综合性能均优于RF、 SVM与MLP。 对比表2的全波段建模结果, RF、 MLP在ReliefF特征选择下的建模测试集Acc高于全波段建模。 然而, 采用另外三种特征选择算法时, RF与MLP的测试集性能反而出现不同程度下降, 提示特征选择策略与模型的适配性对性能至关重要。 HSICLasso-TabPFN模型在特征选择建模中取得了最高测试集Acc为94.31%± 1.08%, 均值对比全波段建模下降1.01%, 同时也取得最低的标准差, 模型较为稳定; 基于PCA的SVM模型测试集Acc为90.60%± 2.06%, 均值对比全波段建模下降1.82%。 这说明特征选择算法能有效降低数据维度、 简化模型复杂度, 但也可能移除对模型预测能力有帮助的特征。 当特征间的相互作用对模型性能至关重要时, 特征选择导致的信息损失在复杂数据集中尤为显著。 SVM、 MLP、 TabPFN三种模型的全波段数据建模展现出优势, 其中TabPFN的双向注意力机制能够有效利用全波段特征之间及样本之间的信息, 在不依赖外部特征选择的情况下, 仍能很好的加权过滤信息, 使模型具有更强的鲁棒性。

表3

Table 3

表3(Table 3)

表3 不同特征选择算法下所有模型预测结果 Table 3 Prediction results of all models under different feature selection algorithms 波段选择方法 建模方法 训练集 测试集 Acc Pre F1 Acc Pre F1 ReliefF SVM 98.28± 0.69 98.36± 0.65 98.31± 0.67 89.16± 1.79 89.53± 1.83 89.28± 1.82 RF 99.85± 0.33 99.86± 0.31 99.85± 0.32 85.27± 2.06 85.69± 1.975 85.20± 2.07 MLP 99.77± 0.18 99.77± 0.18 99.77± 0.18 90.24± 1.91 90.56± 1.95 90.15± 1.96 TabPFN 99.43± 0.22 99.46± 0.22 99.45± 0.22 94.25± 1.14 94.50± 1.06 94.36± 1.16 mRMR SVM 96.17± 2.90 96.34± 2.78 96.27± 2.82 81.14± 2.65 81.89± 2.83 81.46± 2.72 RF 99.97± 0.08 99.98± 0.07 99.98± 0.07 79.04± 2.51 79.60± 2.87 79.17± 2.65 MLP 100± 0 100± 0 100± 0 86.41± 1.86 86.87± 2.03 86.37± 1.90 TabPFN 99.54± 0.28 99.55± 0.27 99.55± 0.27 89.52± 2.18 90.22± 2.37 89.55± 2.27 HSICLasso SVM 98.74± 0.39 98.82± 0.36 98.79± 0.38 89.22± 1.97 89.63± 1.93 89.41± 1.99 RF 99.95± 0.15 99.95± 0.15 99.95± 0.15 83.47± 2.18 84.04± 2.06 83.61± 2.14 MLP 99.97± 0.08 99.97± 0.08 99.97± 0.08 86.71± 2.28 87.28± 2.21 86.59± 2.33 TabPFN 99.59± 0.24 99.60± 0.23 99.60± 0.23 94.31± 1.08 94.54± 0.98 94.37± 1.07 PCA SVM 99.00± 1.07 99.02± 1.03 99.02± 1.04 90.60± 2.06 90.88± 1.95 90.59± 2.03 RF 100± 0 100± 0 100± 0 77.54± 2.41 77.65± 2.19 77.22± 2.34 MLP 99.95± 0.10 99.95± 0.10 99.95± 0.10 83.95± 2.44 84.46± 2.42 84.00± 2.44 TabPFN 99.18± 0.43 99.17± 0.45 99.17± 0.45 91.32± 1.08 91.49± 1.15 91.22± 1.18

表3 不同特征选择算法下所有模型预测结果 Table 3 Prediction results of all models under different feature selection algorithms

图6展示了全波段最优模型FOD-TabPFN与特征选择最优模型FOD-HSICLasso-TabPFN的测试集平均混淆矩阵。 实验结果表明, 全波段模型存在明显的跨类别误判现象, 例如将类别0误判为3类或4类, 将类别2误判为0类等, 这可能是由于全波段特征中包含的噪声引入了跨类别伪关联, 导致模型决策边界模糊。 相比之下, 经过HSICLasso特征选择算法处理后的模型, 其误判情况严格局限于相邻类别之间(如0类与1类、 1类与2类之间), 显著改善了错误分布模式。 这一现象说明HSICLasso算法通过筛选具有强判别力的特征子集, 有效消除了冗余特征和噪声的干扰, 不仅实现了特征降维, 更重要的是优化了模型的错误类型分布。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 TabPFN测试集平均混淆矩阵 (a): FOD-TabPFN; (b): FOD-HSICLasso-TabPFNFig.6 The average confusion matrices of TabPFN on the test set (a): FOD-TabPFN; (b): FOD-HSICLasso-TabPFN

FOD-HSICLasso-TabPFN框架在几乎不损失分类精度的前提下, 显著降低了模型复杂度, 减少了过拟合风险, 同时提高了模型的可解释性和可靠性, 为高光谱数据分类提供了一种有效且实用的特征选择与分类联合解决方案。

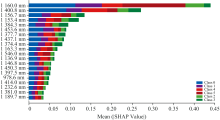
对基于全波段的最佳模型FOD-TabPFN进行可解释性分析, 通过不同特征变量的对模型的SHAP值估计叶片光谱与叶片机理的关系。 图7展示了全波段中贡献排名前20的关键光谱波段的SHAP值分布, 其横轴表示各波段对模型输出的平均贡献度, 纵轴将特征波段按贡献度从高到低排序。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 FOD-TabPFN特征重要性排序Fig.7 The ranking of feature importance of the FOD-TabPFN model

结果显示: 病害等级0级与1级、 4级与5级、 2级与3级之间具有相似的波段贡献规律, 其平均贡献值分别为较低、 中等和较高, 表明模型在区分相邻病害等级时可能依赖相似的光谱响应机制; 高贡献值特征波段主要集中在1 135~1 165和1 370~1 455 nm区间, 该区域对应O— H、 C— H等化学键的伸缩振动及第一泛音吸收带, 与叶片中淀粉、 糖、 木质素及水分等组分的浓度变化相关^[25]。 研究表明: 在PM胁迫下叶片碳水化合物含量变化明显、 细胞结构受到影响。 SHAP分析出的高贡献波段与图5中不同特征选择算法的筛选出的特征波段存在部分重复波段, 不同的是, FOD-TabPFN是基于全波段建模, 剩余的194个波段中也存在对模型有贡献的波段, TabPFN这种对全局特征进行加权处理的方式, 使其在关注局部特征的同时, 也能捕捉全局特征。 同时, 上述高贡献波段与胡等使用高光谱结合机器学习对橡胶叶片进行氮元素反演提取的敏感波段高度吻合^[26]。 说明FOD-TabPFN能有效捕获PM侵染过程中病原菌对叶片造成的生理响应, 其中包括营养含量变化及细胞结构损伤等病理过程。