基于改进窄谱带方法的类核巡航导弹尾焰红外光谱辐射特性研究

引用本文

杨杰, 白璐, 李金录, 刘睿曦. 基于改进窄谱带方法的类核巡航导弹尾焰红外光谱辐射特性研究[J]. 光谱学与光谱分析, 2025,45(12): 3324-3331.
YANG Jie, BAI Lu, LI Jin-lu, LIU Rui-xi. Study on Infrared Spectral Radiation Characteristics of Exhaust Plumes From Nuclear-Like Cruise Missiles Based on Modified Narrow-Band Method[J]. Spectroscopy and Spectral Analysis, 2025,45(12): 3324-3331.
Doi:10.3964/j.issn.1000-0593(2025)12-3324-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于改进窄谱带方法的类核巡航导弹尾焰红外光谱辐射特性研究

杨杰, 白璐^*, 李金录, 刘睿曦

西安电子科技大学物理学院, 陕西西安 710071

*通讯作者 e-mail: blu@xidian.edu.cn

作者简介: 杨杰, 2001年生, 西安电子科技大学物理学院硕士研究生 e-mail: yangjie01@stu.xidian.edu.cn

收稿日期: 2025-04-22 修回日期: 2025-09-15

基金: 国家自然科学基金项目(62405230, 62571411)资助

摘要

提出了一种基于修正函数的改进窄谱带计算模型, 用于两类核巡航导弹尾焰红外辐射的计算。该模型将Curtis-Godson(CG)近似中窄谱带参数替换为路径等效的窄谱带参数, 以解决处理非均匀燃烧系统时精度下降问题。与文献[1]中实验数据对比, 基于修正函数的改进窄谱带模型比传统CG近似下窄谱带模型更符合实验数据, 在2.7、 4.3和3~5 μm波段精度分别提升了13.29%、 18.01%和8.4%。在此基础上, 计算类AGM-86B型导弹和类AGM-158B型导弹沿弹道点变化的流场参数, 采用“line of sight (LOS)”求解辐射传输方程, 建立类核巡航导弹尾焰红外辐射计算模型, 对两类导弹1~20 km飞行高度下尾焰的红外辐射特性进行计算与分析。研究结果表明, 类AGM-86B型导弹在2.7和4.3 μm波段的辐射强度随高度变化趋势基本一致, 在飞行弹道后半段5 km时辐射信号达到峰值。类AGM-158B型导弹在20~1 km飞行弹道内, 4.3 μm波段的辐射强度均大于2.7 μm波段。研究结果可为两类导弹发射初期型号识别与拦截提供理论支撑。

关键词: 改进的窄谱带模型; 尾焰; 红外辐射; Curtis-Godson(CG)近似; 数值模拟

中图分类号:O433.4 文献标志码:A

Study on Infrared Spectral Radiation Characteristics of Exhaust Plumes From Nuclear-Like Cruise Missiles Based on Modified Narrow-Band Method

YANG Jie, BAI Lu^*, LI Jin-lu, LIU Rui-xi

School of Physics, Xidian University, Xi'an 710071, China

*Corresponding author

Abstract

This paper proposes an improved narrow-band model based on a correction function for calculating infrared radiation from two types of nuclear cruise missile plumes. The model replaces narrow-band parameters in the Curtis-Godson (CG) approximation with path-equivalent narrow-band parameters to address accuracy degradation in non-uniform combustion systems. Compared with experimental data from Reference^[1], the improved narrow-band model with correction function demonstrates better alignment with experimental results than traditional CG-based narrow-band models, showing accuracy improvements of 13.29%, 18.01%, and 8.4% in the 2.7, 4.3, and 3~5 μm bands, respectively. Building on this foundation, flow field parameters varying along trajectory points for AGM-86B-type and AGM-158B-type missiles are calculated. By solving the radiative transfer equation using the Line of Sight (LOS) method, an infrared radiation calculation model for nuclear cruise missile plumes is established, enabling computation and analysis of infrared radiation characteristics at flight altitudes ranging from 1 to 20 km. Results indicate that for AGM-86B-type missiles, radiation intensities in the 2.7 and 4.3 μm bands exhibit similar altitude-dependent trends, reaching peak signals at 5 km altitude during the latter half of the flight trajectory. For AGM-158B-type cruise missiles during their flight trajectory from 20 to 1 km, the radiation intensity in the 4.3 μm band is consistently higher than that in the 2.7 μm band. These findings provide theoretical support for early-stage missile type identification and interception of these two missile categories.

Keyword: Improved narrow-band model; Plume; Infrared radiation; Curtis-godson approximation; Numerical simulation

文章图片

引言

类AGM-86B型导弹和类AGM-158B型导弹作为美国“ 三位一体” 核力量的一部分^{[2, 3, 4]}, 是现代战争中执行“ 首波打击” 和摧毁高价值目标的核心装备。这两类导弹通过采用雷达吸波材料、气动外形隐身设计, 干扰诱饵, 大幅降低了雷达发现距离^[5], 采用雷达侦测手段完成这类目标的发现和辨识较为困难。然而, 导弹高温排气尾焰温度远高于背景环境, 同时尾焰的燃烧产物(如CO₂、 H₂O)发生振-转跃迁产生辐射光谱, 在红外波段形成显著的辐射特征^{[6, 7]}, 这类特性使导弹尾焰难以通过传统抑热手段实现完全遮蔽, 为其探测和识别提供了可能。

国内外研究机构及学者对飞行器排气系统红外辐射开展了大量研究^{[8, 9, 10, 11]}。刘尊洋等^[12]研究了飞行高度对液体火箭发动机尾焰特征波段红外辐射特征的影响, 发现飞行高度对4.2~4.7 μ m波段辐射强度影响比2.5~3.0 μ m波段大。包醒东等^[13]研究了飞行高度对固体火箭发动机红外辐射的影响, 发现2.7和4.3 μ m两个谱带的辐射强度随高度变化不一致。牛青林等^[14]对Atlas-Ⅱ 型液体火箭发动机5~70 km范围内尾焰辐射特性进行了分析, 发现随高度变化的尾焰红外特征可用于火箭型号识别。然而, 根据飞行高度、发动机类型和特征谱段影响下具体核巡航导弹的尾焰红外辐射特征, 推演其型号探测与识别的有效途径这一问题, 尚需进一步研究。

目前, “ line by line” ^[15]是计算红外辐射最精确的方法, 该方法通过逐条计算所有光谱线的辐射贡献实现高计算精度, 但计算效率较低。为了平衡计算效率与光谱分辨率, 传统的统计窄谱带模型^[16]逐渐被用来解决光谱辐射问题, 国内外学者对其开展了大量研究^{[17, 18, 19, 20]}。然而, 传统的统计窄谱带模型仅适用于均匀介质, 对于非均匀尾焰, 可采用Curtis-Godson(CG)近似方法^[21]对路径平均窄带参数进行计算, 该方法已广泛应用于尾焰红外特征建模。 CG近似下的统计窄谱带模型对非均匀介质中温度/压力的强梯度变化非常敏感, 这种敏感性会导致光程中间路径的吸收被高估^[22], 如图1所示, 在H₂O的3 755 cm^-1吸收带附近, 窄带模型计算的透过率与LBL相比, 最多相差了20%。针对这一局限性, Ludwig和Malkmus等^[23]将光谱区间内强度相近的谱线分为一组, 并将各组透过率的乘积视为总透过率, 以获取更符合实际工况的路径平均吸收系数。 Hartman等^[22]发现路径平均半宽对介质热力学状态具有敏感性, 这可能是导致吸收系数被高估的重要原因。 Yamamoto等^[24]研究发现, 在吸收介质呈典型分布的大气路径下, 通过引入修正系数获取更小的平均半宽可以提高CG近似的计算精度。

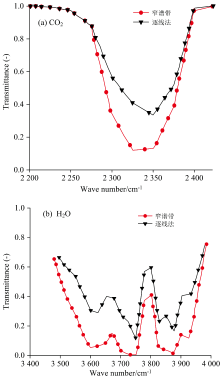	Figure Option View Download New Window
	图1 不同模型计算透过率结果^[22] (a): CO₂; (b): H₂OFig.1 Transmittance calculation results of different models^[22] (a): CO₂; (b): H₂O

实际上, 尾焰高温、高压及强梯度的热力学状态与大气环境存在本质差异, 这将导致平均半宽对介质热力学状态(温度与总压力)的敏感性显著增强, 在非均匀高温高压尾焰中尤为突出。因此, 提出了一种精确的尾焰红外辐射模型, 通过引入与非均匀路径热力学状态相关的修正函数计算窄带辐射特性, 以解决CG近似下的统计窄谱带模型在处理强梯度变化的尾焰介质时精度下降问题。同时, 将该模型用于类AGM-86B型导弹和类AGM-158B型导弹真实型号的辐射特性系统研究, 分析探测波段和飞行高度对两类核巡航导弹红外辐射特征的影响。

1 物理模型

1.1 流场计算模型

所涉及的低空域飞行器绕流场和发动机尾焰流场符合连续流动假设, 基于可压缩雷诺平均的Navier-Stokes方程即可满足计算, 方程组包含质量方程、动量方程和能量方程。考虑复燃反应的多分量质量守恒方程采用如式(1)形式

$\frac{\partial (ρ Y_{i})}{\partial t} + \nabla (ρ \vec{v} Y_{i}) = \nabla (D_{i} \nabla (ρ Y_{i})) + R_{i}$ (1)

式(1)中, ρ 为气体的密度; Y_i为单个气体组分i的质量分数; $\vec{v}$ 为速度矢量; D_i为组分i的扩散系数; R_i表示化学反应引起的组分气体i的净生成率。

动量守恒方程为

$\frac{(\rho v)}{t}+\nabla\left(\rho v v=-\nabla p+\nabla(\tau)-\nabla\left(\rho \overline{u_{i}^{\prime} u_{j}^{\prime}}\right)\right.$(2)

式(2)中, $-\rho \overline{u_{i}^{\prime} u_{j}^{\prime}}$为雷诺应力, p为流体微元体上的静压强; $\vec{τ}$ 是作用在单个流体介质上的粘性张量, 表达式为

$\vec{τ} = τ_{ij} = [μ (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})] - \frac{2}{3} μ \frac{\partial u_{k}}{\partial x_{k}} δ_{ij}$ (3)

式(3)中, δ _ij为克罗内克符号, μ 为流体的粘性系数。

能量守恒方程为

$\begin{array}{l} \frac{\partial}{\partial t} (ρE) + \nabla (\vec{v} (ρE + p)) = \\ \nabla (k_{eff} \nabla T - \sum_{j} {\overset{̅}{h}}_{j} {\vec{J}}_{j} + ({\overset{̅}{τ}}_{eff} \vec{v})) + S_{g} + S_{p} \end{array}$ (4)

式(4)中, $\frac{\partial (ρE)}{\partial t}$ 代表总能量随时间的变化; $\nabla (\vec{v} (ρE + p))$ 表示动能和压力做功; $k_{eff}$ 为有效导热系数; $T$ 为热力学温度; ${\overset{̅}{h}}_{j}$ 为组分的焓值; ${\vec{J}}_{j}$ 为组分的湍流导热系数; ${\overset{̅}{τ}}_{eff}$ 为偏应力张量; $\vec{v}$ 为速度矢量; $S_{g}$ 和 $S_{p}$ 分别表示化学反应和颗粒带来的能量转移; $k_{eff} \nabla T$ 为导热和对流带来的能量转移。

总能量E表达式为

$E = \vec{h} - \frac{P}{ρ} + \frac{| \vec{v} |^{2}}{2}$ (5)

1.2 基于修正函数的窄谱带计算模型

在传统统计窄带模型^[25]的基础上, 为了处理非均匀燃烧系统精度下降问题, 引入与尾焰非均匀路径相关的修正函数, 提出了基于修正函数的尾焰红外辐射计算模型。光谱间隔Δ η 下, 沿非均匀路径的窄带透过率 ${\overset{̅}{τ}}_{Δ η}$ 为

$\bar{\tau}_{\Delta \eta}=\exp \left[-\frac{2 \bar{\gamma}_{\Delta \eta}}{\bar{d}_{\Delta \eta}}\left(\sqrt{1+\frac{u \bar{\kappa}_{\Delta \eta} ~~\bar{d}_{\Delta \eta}}{\bar{\gamma}_{\Delta \eta}}}-1\right)\right]$(6)

式(6)中, ${\overset{̅}{κ}}_{Δ η}$ 为等效吸收系数, ${\overset{̅}{γ}}_{Δ η}$ 为等效半宽, ${\overset{̅}{d}}_{Δ η}$ 为等效谱线间隔。 CG近似下的传统窄谱带模型在强线吸收和弱线吸收两种情况下结果较为准确, 但会高估中间区域的吸收。基于修正函数的路径平均等效半宽参数具体表达式为

$ζ (x_{CG}) = {(\frac{x_{CG}}{1 + x_{CG}})}^{a}$ (7)

式(7)中, a为与非均匀尾焰中辐射组分分布相关的常数。当a=0时, ζ =1, 退化为传统窄谱带方法。

$x_{\mathrm{CG}}=\frac{\kappa_{\Delta \eta}~~ u}{2 \pi \gamma_{\Delta \eta}}$(8)

$u = \int_{s_{1}}^{s_{2}} p (s) d s$ (9)

式中, x_CG为与尾焰热力学状态相关的谱线强度参数, p(s)为分压, u为压力路径长度, s表示路径位置。

因此, 修正后的等效半宽 ${\overset{̅}{γ}}_{Δ η}$ 可表示为

$({\overset{̅}{γ}}_{Δ η})^{ζ} = \frac{1}{u {\overset{̅}{κ}}_{Δ η}} \int_{s_{1}}^{s_{2}} p (s) {\overset{̅}{κ}}_{Δ η} (s) ({\overset{̅}{γ}}_{Δ η})^{ζ} (s) d s$ (10)

等效吸收系数 ${\overset{̅}{κ}}_{Δ η}$ 和等效谱线间隔 ${\overset{̅}{d}}_{Δ η}$ 由式(11)和式(12)给出

${\overset{̅}{κ}}_{Δ η} = \frac{1}{u} \int_{s_{1}}^{s_{2}} p (s) {\overset{̅}{κ}}_{Δ η} (s) d s$ (11)

${\overset{̅}{d}}_{Δ η} = \frac{1}{u {\overset{̅}{κ}}_{Δ η}} \int_{s_{1}}^{s_{2}} p (s) {\overset{̅}{κ}}_{Δ η} (s) {\overset{̅}{d}}_{Δ η} (s) d s$ (12)

式(11)和式(12)中, ${\overset{̅}{κ}}_{Δ η}$ , ${\overset{̅}{γ}}_{Δ η}$ 和 ${\overset{̅}{d}}_{Δ η}$ 可通过Young^[26]的谱带模型方法直接计算。

基于以色列先进研发机构的BEM-Ⅱ 发动机地面试车数据^[1], 对修正后窄谱带计算模型的可靠性进行验证, 关于该数值模拟所涉及的详细计算模型及边界条件参数, 可参考作者所在课题组此前发表的文献^[27], 本文不再重复阐述。图2给出了CG近似下窄谱带方法、改进的窄谱带方法和实验数据的对照, 从图2中可以看出, 两种窄谱带方法的计算结果趋势相同, 但改进的窄谱带模型更符合实验数据。表1所示为两种窄谱带模型在2.7、 4.3和3~5 μ m波段的相对误差分布, 从表中可以看出改进的窄谱带模型在2.7、 4.3和3~5 μ m波段精度分别提升了13.29%、 18.01%和8.4%, 改进的窄谱带方法在红外波段具有良好的性能。

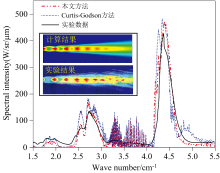	Figure Option View Download New Window
	图2 BEM-Ⅱ 红外辐射图像和光谱辐射强度计算值与实验值比较Fig.2 Comparison between calculated and experimental values of BEM-Ⅱ infrared radiation images and spectral radiation intensity

表1 不同波段相对误差分布 Table 1 Distribution of relative errors for different spectral bands

1.3 尾焰红外辐射计算模型

涉及的尾焰流场为纯气相, 不包含颗粒等散射介质, 根据辐射传输理论, 当介质中仅存在吸收、发射效应时辐射传输方程为

$\frac{d I_{λ} (s)}{d s} = {\overset{̅}{κ}}_{Δ η} I_{bλ} (s) - {\overset{̅}{κ}}_{Δ η} I_{λ} (s)$ (13)

式(13)中, I_λ(s)和I_bλ(s)表示光谱辐射强度和黑体辐射强度。

对公式求解可得到通过路径L后的辐射强度

$I_{λ} (s) = - \int_{0}^{L} I_{bλ} (s) \frac{\partial τ}{\partial s} d s$ (14)

式(14)中, τ 对应式(6)中的窄带透过率。

采用line of sight (LOS)方法求解辐射传输方程, 该方法基本思想为, 将射线沿探测方向与流场相交部分分为n层, 通过逐步递推对每层介质的吸收-发射效应进行累积计算, 并逐层叠加获得传播路径终端的积分辐射强度。

文献[28]给出了第n层累积辐射强度的离散化表达式为

$I_{n} = I_{n - 1} τ_{n} + I_{b}^{n} (1 - τ_{n})$ (15)

式(15)中, I_n_-1为第n-1层的辐亮度, $I_{b}^{n}$ 为第n层的黑体辐射源函数, τ _n为第n层的介质透过率。

2 计算条件

2.1 几何尺寸

类AGM-86B型导弹弹体呈细长圆柱形, 头部圆钝, 尾部逐渐收窄, 以减小空气阻力, 其几何结构示意图如图3(a)所示。类AGM-158系列导弹头部呈尖锥形, 弹体上窄下宽, 并经过圆角处理, 其几何结构示意图如图3(b)所示。通过局部细化方法, 对导弹外形进行建模, 两型核巡航导弹几何参数见表2。

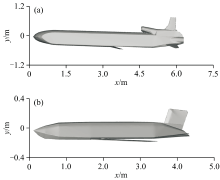	Figure Option View Download New Window
	图3 几何结构示意图 (a): 类AGM-86B型; (b): 类AGM-158B型Fig.3 Schematic diagram of geometric configuration (a): AGM-86B-type; (b): AGM-158B-type

表2 类AGM-86B型和类AGM-158B型导弹技术参数表 Table 2 Technical parameter table of AGM-86B-type and AGM-158B-type missiles

2.2 计算域及边界条件

考虑到几何的不对称性和全模型仿真的精度, 采用全模型进行计算建模。计算域选取半径为10 m的球形, 基于非结构化网格进行全流域网格划分, 对机头、机翼及壁面等流-固交界处进行网格加密, 边界层数量设定为21层, 两类导弹对应的面网格分布如图4所示。

	Figure Option View Download New Window
	图4 面网格示意图 (a): 类AGM-86B型; (b): 类AGM-158B型Fig.4 Surface mesh schematic diagrams (a): AGM-86B-type; (b): AGM-158B-type

对类AGM-86B型导弹和类AGM-158型导弹进行壁面绕流场及尾焰流场仿真, 计算域入口为无限远处自由来流, 设置为压力远场, 发动机喷口处为压力入口, 计算域出口为压力出口。其中, AGM-86B采用F107-WR-101涡扇发动机, 燃料为JP-9, AGM-158B采用F107-WR-105涡扇发动机, 燃料为JP-4, 两类燃料的典型特性^[29]如表3所示。

表3 两类燃料典型特性^[29] Table 3 Typical characteristics of two types of fuels^[29]

2.3 流场参量求解方法

基于连续域计算流体力学(CFD)的雷诺平均(RANS)方法, 计算两类导弹的流场分布, 采用两方程realizable k-ε 湍流模型, 该模型计算了包括湍流和化学反应在内的可压缩流动。考虑到湍流/喷焰相互作用的复杂性, 选用取8组分、 10反应的有限速率化学动力模型, 即采用考虑O、 H、 OH、 CO、 CO₂、 H₂O、 O₂和H₂组分的H₂/CO/O₂反应体系。以燃烧室温度、压强, 及推进剂配比为输入, 采用NASA开发的CEA代码^[30], 计算获得喷嘴处的温度、压强和特征组分摩尔分数。表4所示为两类导弹喷口处详细工况。

表4 两类导弹发动机喷口处工况参数 Table 4 Operational parameters at nozzle exits of two types of missile

边界条件类型包括压力入口、压力出口、压力远场以及无滑移壁面条件, 基于以上参量设置, 对两类导弹H=3 km时以0.8 Ma巡航态工况飞行时进行流场仿真。

3 结果与讨论

3.1 两类导弹三维流场特性分布

在喷焰红外特性研究中, 流场热力学参数对其辐射强度具有决定性作用, 其中, 温度和燃烧产物的组分构成尤为关键。图5(a)和(b)分别给出了海拔高度H=3 km工况下两类导弹三维温度场及典型燃烧产物(H₂O、 CO₂)的摩尔分数。由图5可以看出, 类AGM-158B型导弹尾焰核心区较AGM-86B更长, 尾焰温度低, 特征组分H₂O和CO₂含量更少。这是由于F107-WR-105涡扇发动机通过外涵道引入大量冷空气与高温燃气混合, 显著降低了尾焰温度, 同时低烟推进剂有效减少了辐射特征组分(H₂O、 CO₂)的排放。

	Figure Option View Download New Window
	图5 流场主要参数分布图 (a): 类AGM-86B型; (b): 类AGM-158B型Fig.5 Distribution diagrams of key flow field parameters (a): AGM-86B-type; (b): AGM-158B-type

3.2 两类导弹喷口下游轴向流场特征分布

为了详细分析两类导弹尾焰演变规律, 提取3.1节工况下两类导弹喷焰下游轴向3 m位置处的温度、 H₂O和CO₂摩尔分数分布如图6所示。对类AGM-86B型导弹来说, 温度在离喷口25 cm附近出现短暂抬升, 同时CO₂含量提高了约0.006, 这是由于尾焰与空气混合后, 未燃烧充分的还原性气体与空气中的O₂发生复燃反应, 导致温度和CO₂含量发生相应的升高。对类AGM-158B型导弹来说, 在尾焰与空气掺混后, 温度和特征组分未发生明显变化, 说明其燃料燃烧更充分。类AGM-86B型导弹相较于类AGM-158B型导弹, 在最高点温度上相差500 K, H₂O、 CO₂特征组分上相差一个数量级, 这势必会导致两者在辐射强度上产生较大差异。

	Figure Option View Download New Window
	图6 尾喷口下游轴向位置流场分布 (a): 温度; (b): H₂O摩尔分数; (c): CO₂摩尔分数Fig.6 Flow field distributions at downstream axial positions of nozzle exit (a): Temperature; (b): H₂O molar fraction; (c): CO₂ molar fraction

3.3 两类导弹尾焰红外辐射强度分布

图7(a)和(b)分别给出了类AGM-86B型导弹和类AGM-158B型导弹在H=3 km巡航状态下尾焰的辐射图像。从上到下分别对应2.7、 4.3、 3~5和8~12 μ m四个特征波段的红外图像。由图7可以看出, 两类导弹在3~5 μ m波段辐射信号最强, 4.3 μ m波段次之, 8~12 μ m波段最弱。 3~5 μ m 波段较8~12 μ m波段高出两个数量级。类AGM-86B型导弹在四个特征波段辐射强度均大于类AGM-158B, 这是由于高碳氢比和高热值燃料会导致喜焰温度升高, 生成更多CO₂, 从而引起两者温度和特征组分含量产生差异。牛青林等^[31]研究不同发动机运行条件下尾焰红外辐射特性时, 证明了改变燃料配比会对尾焰红外辐射特性产生显著影响。

	Figure Option View Download New Window
	图7 特征谱带辐射图像 (a): 类AGM-86B型; (b): 类AGM-158B型Fig.7 Radiation images in characteristic spectral bands (a): AGM-86B-type; (b): AGM-158B-type

3.4 沿弹道点变化的两类导弹尾焰辐射强度

空射导弹发射初期飞行弹道非定常, 发射高度覆盖广, 如类AGM-158B型导弹可在300~12 000 m范围内发射, 在不同高度巡航态下, 两类导弹尾焰辐射强度呈现出沿弹道点变化的规律。图8给出了1.5~8 μ m波长范围内, 两类导弹在20~1 km飞行弹道下以0.8马赫速度飞行时的尾焰光谱辐射强度曲线。由图8可知, 两类导弹沿弹道点变化的光谱辐射强度表现出气体选择性发射谱结构, 辐射能量主要集中在2.7、 4.3和5~8 μ m波段内。类AGM-86B型导弹沿弹道点变化的辐射强度峰值比类AGM-158型导弹高出一个数量级, 二者在执行同一作战任务时, 类AGM-86B型导弹更容易被探测到。这是由于较AGM-158B使用的JP-4燃料, AGM-86B所采用的JP-9燃料热值更高, 燃烧时尾焰温度和特征组分浓度更高, 进而引起两类导弹辐射强度数量级上的差异。

	Figure Option View Download New Window
	图8 不同飞行弹道(H=20~1 km)下光谱辐射强度 (a): 类AGM-86B型; (b): 类AGM-158型Fig.8 Spectral radiation intensities under different flight trajectories (H=20~1 km) (a): AGM-86B-type; (b): AGM-158B-type

为了对比两类导弹在同一任务中特征波段辐射强度的差异, 表5给出了两类导弹在2.7 μ m波段和4.3 μ m波段的辐射特性。由表5可知, AGM-87B两个谱段辐射强度在1~5 km 时逐渐增强, 在5 km巡航态时最大, 达到了432.26 W· sr^-1, AGM-158B在2.7 μ m带呈线性增长, 这是尾焰燃烧产物H₂O增多引起的, 而在4.3 μ m带变化趋势较平缓, 说明随高度的变化尾焰中CO₂含量变化不大。

表5 两类导弹特征谱段积分辐射强度 Table 5 The integral radiation intensities of characteristic spectral bands for two types of missiles

4 结论

提出了一种处理非均匀燃烧系统时基于修正函数的改进窄谱带计算模型, 以类AGM-86B型导弹和类AGM-158B型导弹为研究对象, 开展两类导弹流场数值模拟, 通过建立红外辐射传输模型, 揭示了两类导弹尾焰红外辐射的弹道演化规律, 结论如下:

(1)以BEM-Ⅱ 类发动机地面试车实验数据为基准, 基于修正函数的窄谱带模型比CG近似下的窄谱带模型更符合实验数据, 在2.7、 4.3和3~5 μ m波段精度分别提升了13.29%、 18.01%和8.4%。

(2)在H=3 km工况下, 类AGM-86B型导弹在2.7、 4.3、 3~5和8~12 μ m四个特征波段辐亮度均比类AGM-158B型导弹高出一个数量级, 二者的辐亮度峰值都出现在3~5 μ m 波段。

(3)类AGM-86B型导弹和类AGM-158B型导弹在20~1 km范围内4.3 μ m波段的辐射强度均大于2.7 μ m波段, 在后续相似亚音速导弹进行探测和识别时, 4.3 μ m波段可作为重点关注的波段。

参考文献

文献列表

[1]	Avital G, Cohen Y, Gamss L, et al. Journal of Thermophysics and Heat Transfer, 2001, 15(4): 377. [本文引用:1]
[2]	Lowther A B. Strategic Studies Quarterly, 2017, 11(3): 34. [本文引用:1]
[3]	Evans D, Schwalbe J. The Long-Range Stand off (LRSO) Cruise Missile and Its Role in Future Nuclear Forces, Applied Physics Laboratory, Johns Hopkins University, 2017. [本文引用:1]
[4]	Majumdar S. Vayu Aerospace and Defence Review, 2021, (1): 128. [本文引用:1]
[5]	LIU Ying(刘颖). Aerodynamic Missile Journal(飞航导弹), 2013, (11): 12. [本文引用:1]
[6]	CAI Hong-hua, NIE Wan-sheng, SU Ling-yu, et al(蔡红华, 聂万胜, 苏凌宇, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(7): 1999. [本文引用:1]
[7]	Li J, Bai L, Zhang L, et al. International Journal of Heat and Mass Transfer, 2023, 216: 124606. [本文引用:1]
[8]	Zhang W, Shuai Y, Gao P, et al. Infrared Physics & Technology, 2024, 139: 105312. [本文引用:1]
[9]	Zhu T, Sun Y, Niu Q, et al. International Journal of Heat and Mass Transfer, 2024, 229: 125663. [本文引用:1]
[10]	Chen Y, He B, Liu L, et al. International Journal of Heat and Mass Transfer, 2025, 241: 126765. [本文引用:1]
[11]	Hou S, Wang Q, Hu H, et al. International Journal of Thermal Sciences, 2025, 210: 109567. [本文引用:1]
[12]	LIU Zun-yang, SHAO Li, WANG Ya-fu, et al(刘尊洋, 邵立, 汪亚夫, 等). Acta Optica Sinica(光学学报), 2013, 33(4): 9. [本文引用:1]
[13]	BAO Xing-dong, YU Xi-long, WANG Zhen-hua, et al(包醒东, 余西龙, 王振华, 等). Journal of Propulsion Technology(推进技术), 2021, 42(3): 569. [本文引用:1]
[14]	Niu Q, Duan X, Meng X, et al. Infrared Physics & Technology, 2019, 99: 28. [本文引用:1]
[15]	Ibgui L, Hartmann J-M. Journal of Quantitative Spectroscopy and Radiative Transfer, 2002, 75(3): 273. [本文引用:1]
[16]	Rivière P, Soufiani A. International Journal of Heat and Mass Transfer, 2012, 55(13-14): 3349. [本文引用:1]
[17]	Zheng S, Yang Y, Zhou H. International Journal of Heat and Mass Transfer, 2019, 129: 1232. [本文引用:1]
[18]	Qi C, Zheng S, Zhou H. Journal of Quantitative Spectroscopy and Radiative Transfer, 2017, 197: 45. [本文引用:1]
[19]	Zheng S, Zhang M, Na M, et al. ES Energy & Environment, 2022, 17(4): 33. [本文引用:1]
[20]	Zheng S, Sui R, Sun Y, et al. ES Energy & Environment, 2021, 12(2): 4. [本文引用:1]
[21]	Krakow B, Babrov H J, Maclay G J, et al. Applied Optics, 1966, 5(11): 1791. [本文引用:1]
[22]	Soufiani A, Hartmann J M, Taine J. Journal of Quantitative Spectroscopy and Radiative Transfer, 1985, 33(3): 243. [本文引用:2]
[23]	Ludwig C B, Malkmus W, Reardon J, et al. Hand book of Infrared Radiation from Combustion Gases, Washington: Space Administration, 1973. [本文引用:1]
[24]	Yamamoto G, Aida M, Yamamoto S. Journal of Atmospheric Sciences, 1972, 29(6): 1150. [本文引用:1]
[25]	Malkmus W. Journal of the Optical Society of America, 1967, 57(3): 323. [本文引用:1]
[26]	Young S J. Journal of Quantitative Spectroscopy and Radiative Transfer, 1977, 18(1): 1. [本文引用:1]
[27]	Li J, Bai L, Bai J, et al. Infrared Physics & Technology, 2022, 125: 104260. [本文引用:1]
[28]	Sun Y, Niu Q, Zhu T, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2024, 328: 109146. [本文引用:1]
[29]	Burdette G W, Land er H R, McCoy J R. Journal of Energy, 1978, 2(5): 289. [本文引用:1]
[30]	Gordon S, McBride B J. Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications. Part 1: Analysis, NASA Reference Publication 1311, 1994. [本文引用:1]
[31]	Niu Q, He Z, Dong S. Chinese Journal of Aeronautics, 2017, 30(3): 1101. [本文引用:1]

2001

0.0

... 发动机地面试车数据^[1], 对修正后窄谱带计算模型的可靠性进行验证, 关于该数值模拟所涉及的详细计算模型及边界条件参数, 可参考作者所在课题组此前发表的文献^[27], 本文不再重复阐述 ...

2017

0.0

... 核力量的一部分^[2,3,4], 是现代战争中执行#cod#x0201c ...

2017

0.0

... 核力量的一部分^[2,3,4], 是现代战争中执行#cod#x0201c ...

2021

0.0

... 核力量的一部分^[2,3,4], 是现代战争中执行#cod#x0201c ...

2013

0.0

... 这两类导弹通过采用雷达吸波材料、气动外形隐身设计, 干扰诱饵, 大幅降低了雷达发现距离^[5], 采用雷达侦测手段完成这类目标的发现和辨识较为困难 ...

2019

0.0

... 然而, 导弹高温排气尾焰温度远高于背景环境, 同时尾焰的燃烧产物(如CO₂、 H₂O)发生振-转跃迁产生辐射光谱, 在红外波段形成显著的辐射特征^[6,7], 这类特性使导弹尾焰难以通过传统抑热手段实现完全遮蔽, 为其探测和识别提供了可能 ...

2023

0.0

2024

0.0

... 国内外研究机构及学者对飞行器排气系统红外辐射开展了大量研究^[8,9,10,11] ...

2024

0.0

... 国内外研究机构及学者对飞行器排气系统红外辐射开展了大量研究^[8,9,10,11] ...

2025

0.0

... 国内外研究机构及学者对飞行器排气系统红外辐射开展了大量研究^[8,9,10,11] ...

2025

0.0

... 国内外研究机构及学者对飞行器排气系统红外辐射开展了大量研究^[8,9,10,11] ...

2013

0.0

... 刘尊洋等^[12]研究了飞行高度对液体火箭发动机尾焰特征波段红外辐射特征的影响, 发现飞行高度对4 ...

2021

0.0

... 包醒东等^[13]研究了飞行高度对固体火箭发动机红外辐射的影响, 发现2 ...

2019

0.0

... 牛青林等^[14]对Atlas-#cod#x02161 ...

2002

0.0

... ^[15]是计算红外辐射最精确的方法, 该方法通过逐条计算所有光谱线的辐射贡献实现高计算精度, 但计算效率较低 ...

2012

0.0