融合形态学与优化算法的XRF铁矿石品位定量分析检测方法研究

引用本文

王兰豪, 朱震宇, 钟宵, 王红艳, 李朝朋. 融合形态学与优化算法的XRF铁矿石品位定量分析检测方法研究[J]. 光谱学与光谱分析, 2025,45(12): 3307-3316.
WANG Lan-hao, ZHU Zhen-yu, ZHONG Xiao, WANG Hong-yan, LI Zhao-peng. Quantitative Analysis of XRF Iron Ore Grade Combining Morphology and Optimization Algorithms[J]. Spectroscopy and Spectral Analysis, 2025,45(12): 3307-3316.
Doi:10.3964/j.issn.1000-0593(2025)12-3307-10 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

融合形态学与优化算法的XRF铁矿石品位定量分析检测方法研究

王兰豪¹, 朱震宇², 钟宵³, 王红艳^3,^*, 李朝朋⁴

1.中国矿业大学炼焦煤资源绿色开发全国重点实验室, 江苏徐州 221116

2.中国矿业大学人工智能学院, 江苏徐州 221116

3.中国矿业大学信息与控制工程学院, 江苏徐州 221116

4.沈阳隆基智能技术研究有限公司, 辽宁沈阳 110000

*通讯作者 e-mail: wanghongyan@cumt.edu.cn

作者简介: 王兰豪, 1989年生, 中国矿业大学炼焦煤资源绿色开发全国重点实验室副教授 e-mail: wanglanhao@cumt.edu.cn

收稿日期: 2025-07-29 修回日期: 2025-09-27

基金: 国家重点研发计划-政府间国际科技创新合作项目(2025YFE0101100), 辽宁省重点研发项目(2024JH2/102400026)资助

摘要

针对现有X射线荧光光谱(XRF)铁矿石在线品位检测技术受强本底干扰、谱峰重叠解析困难及建模精度不足制约的问题, 提出覆盖“信号预处理—谱峰分解—品位建模”全流程的解决方案。在本底扣除环节, 开发融合数学形态学与导数迭代多项式拟合(Mor+DIPF)方法, 在保障特征峰光谱保真度的同时显著提升基线平滑性与拟合精度, 解决传统形态学算法在特征峰区域平滑不足的缺陷。针对复杂谱峰重叠, 提出自适应参数更新粒子群算法(APU-PSO)联合EM-GMM的分解框架, 通过增强全局寻优能力实现高精度解析, 为后续定量分析提供高精度谱峰参数。为解决基体效应导致的非线性误差问题, 构建Transformer与双向长短期记忆网络(BiLSTM)融合模型, 利用Transformer捕捉工艺变量间的长距离依赖关系, BiLSTM增强时序动态特征学习, 通过多源数据融合深度提取品位波动关键影响因素, 解决基于XRF铁矿石品位高精度预测瓶颈。实验结果表明, Mor+DIPF算法在四种不同基线(线性、正弦、高斯、指数)下的均方根误差(RMSE)、平均相对误差(MAE)和决定系数( R²)均优于传统方法, 其中 R²最高达到99.96%。 APU-PSO-EM-GMM算法在普通重叠峰、肩部重叠峰和多重叠峰的拟合效果上均优于曲线拟合法、高斯锐化法等对比算法。 Transformer-BiLSTM模型对钛铁矿品位的定量分析平均绝对误差为0.217 2, 均方根误差为0.280 7, 决定系数达99.716 1%, 性能优于SVM、 Transformer等模型。该系统已在沈阳某选矿厂应用6个月以上, 在设定3%相对误差范围内的估计合格率均超90%, 展现出高精度、强实时性与优异鲁棒性的综合优势, 该研究成果为复杂矿物在线分析提供了理论依据与技术范例, 推动XRF光谱分析在工业过程检测领域的智能化应用。

关键词: X射线荧光光谱; 本底扣除; 谱峰重叠; Transformer; BiLSTM; 品位检测

中图分类号:O433 文献标志码:A

Quantitative Analysis of XRF Iron Ore Grade Combining Morphology and Optimization Algorithms

WANG Lan-hao¹, ZHU Zhen-yu², ZHONG Xiao³, WANG Hong-yan^3,^*, LI Zhao-peng⁴

1. State Key Laboratory of Coking Coal Resources Green Exploitation, China University of Mining and Technology, Xuzhou 221116, China

2. Artificial Intelligence Research Institute, China University of Mining and Technology, Xuzhou 221116, China

3. School of Information and Control Engineering, China University of Mining Technology, Xuzhou 221116, China

4. LONGi Magnet Co., LTD., Shenyang 110000, China

*Corresponding author

Abstract

This study addresses the limitations of existing X-ray fluorescence spectroscopy (XRF) technology for the online detection of iron ore grade, including strong background interference, difficulty in resolving overlapping spectral peaks, and insufficient modeling accuracy. It proposes a comprehensive solution that covers the entire process, from signal pre-processing and spectral peak decomposition to grade modeling. In the background subtraction stage, a method combining mathematical morphology and derivative-iterative polynomial fitting (Mor+DIPF) has been developed. This method significantly improves baseline smoothness and fitting accuracy, while also ensuring spectral fidelity in the region of characteristic peaks. This addresses the deficiency of traditional morphological algorithms, which do not sufficiently smooth this region. To address complex peak overlap, a particle swarm optimization (PSO) approach with adaptive parameter updates (APU-PSO) is combined with an expectation-maximization (EM) Gaussian mixture model (GMM) decomposition framework. This enhances global optimization capabilities and enables high-precision analysis, providing accurate peak parameters for subsequent quantitative analysis. To address non-linear errors caused by matrix effects, a fusion model combining transformers and bidirectional long short-term memory networks (BiLSTM) is constructed. Transformers capture long-range dependencies among process variables, while BiLSTMs enhance the learning of temporal dynamics. By fusing multi-source data, key factors influencing grade fluctuations are thoroughly identified, overcoming the challenge of accurately predicting iron ore grades using XRF. Experimental results demonstrate that the Mor+DIPF algorithm outperforms traditional methods in terms of root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination ( R²) across four different baselines (linear, sinusoidal, Gaussian, and exponential), with R² achieving a maximum value of 99.96%. The APU-PSO-EM-GMM algorithm outperforms the comparison algorithm.

Keyword: X-ray fluorescence spectroscopy; Background subtraction; Spectral peak overlap; Transformer; BiLSTM; Grade detection

文章图片

引言

钢铁制品作为国民经济和社会发展的重要基础材料产业, 在社会生产和人民生活中占据着不可或缺的地位^[1]。相关统计数据显示, 全球粗钢年产量已突破18亿吨, 其中中国粗钢产量约为9亿吨, 产量占比接近50%^[2]。尽管我国铁矿石储量较为丰富, 但主要以低品位矿石为主, 且矿石类型复杂多样, 导致开采难度大、选矿成本高, 同时面临能耗高和生产效率低等技术难题, 这些因素制约了钢铁工业的高质量发展^{[3, 4]}。

目前, 针对铁矿石品位的定量分析研究方案较为丰富, 多集中于传统化学分析方法, 包括ICP-AES法、 EDTA滴定法、稳健统计法以及碘氟法等^{[5, 6, 7, 8]}。这些方法虽准确可靠, 但存在操作流程复杂、分析成本高、样品预处理繁琐、分析效率低等问题。近年来, 基于光谱的分析方法成为研究热点, 其中包括原子吸收光谱法、原子荧光光谱法和X射线荧光光谱法等^{[9, 10]}。在这其中, X射线荧光光谱法(X-ray fluorescence, XRF)以其快速的检测速度、较低的分析成本和广泛的适用元素范围等优点, 成为矿石元素分析的关键工具之一^[11], 被广泛应用于环境科学、化学以及生物学等多个学科领域, 并在一定程度上取代了传统的化学分析方法^{[12, 13, 14]}。

在进行铁矿石元素XRF分析时, 工程师面临三个显著影响分析结果的问题: 背景信号造成的本底干扰、邻近元素特征峰的重叠, 以及基体效应导致的元素定量分析中的非线性误差, 前两个问题会影响光谱数据的准确性和后续的定量分析结果, 第三个问题则降低定量检测结果精度。针对上述问题, 本文开展基于XRF的铁矿石品位定量分析方法及系统研究。首先从形态学方法和迭代多项式拟合算法进行深入研究, 提出了一种基于形态学与导数迭代多项式拟合的本底扣除方法。其次是在谱线特征峰重叠问题上, 研究者常采用的方法包括曲线拟合法^[15]、导数法^[16]、小波变换法^[17], 这些方法在处理谱线重叠问题上得到了广泛应用。本文从元启发式算法^[18]入手, 提出基于自适应参数更新策略的粒子群优化算法, 结合高斯混合模型, 采用EM算法对重叠峰进行解析。最后在基体效应校正问题上, 选取Transformer融合双向长短时记忆网络实现钛铁矿品位的实时定量分析。

1 XRF光谱本底扣除和重叠峰分解预处理方法

1.1 基于形态学与导数迭代多项式拟合的本底扣除

为解决XRF数据易受到外界干扰、 X射线与样品间相互作用等因素影响造成的本底干扰, 提出了一种基于形态学与导数迭代多项式拟合的本底扣除方法, 确保精确获取目标元素的光谱谱峰及其净峰面积。形态学方法虽能够较好地保留光谱特征, 但在特征峰区域的本底信号平滑处理上仍有待提升; 相比之下, 四阶导数迭代多项式拟合方法在处理平缓变化的本底信号时, 能够更完整地分离特征峰信息, 从而显著提高本底拟合的精确度。

形态学的基本运算包括侵蚀、膨胀、开运算和闭运算, 这些运算构成了形态学算法的基础框架。通过分析信号的局部结构, 这些操作可以有效提取和描述光谱信号中的形态特征。此过程中, 结构元素Y_s被定义为一个以通道地址点i为中心的可移动窗口, 窗口的半宽为L_s(全宽则为2L_s+1), 其中S_i表示光谱信号S在第i个通道地址上的值。

侵蚀操作E(S_i)定义为

$E (S_{i}) = \min (S_{i + j}), j = - L_{s}, - L_{s} + 1, \dots, L_{s}$ (1)

膨胀操作D(S_i)定义为

$D (S_{i}) = \max (S_{i + j}), j = - L_{s}, - L_{s} + 1, \dots, L_{s}$ (2)

开运算O(S_i)定义为

$O (S_{i}) = D (E (S_{i}))$ (3)

P运算P(S_i)定义为

$P (S_{i}) = \frac{D [O (S_{i})] + E (O (S_{i}))}{2}$ (4)

从图1可知, P运算在光谱特征保留方面具有一定优势, 但存在显著不足: 部分区间运算结果高于原始光谱信号; 在谱峰区域易出现强度突变, 导致提取的本底信号平滑性较差。

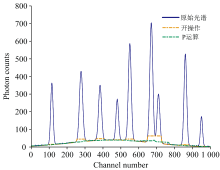	Figure Option View Download New Window
	图1 形态学P运算、开操作与原始光谱对比示意图Fig.1 Diagram comparing morphological P operation, open operation and original spectrum

为了提取适用于分析的背景光谱, 本文提出了一种4阶导数迭代多项式拟合方法, 采用多项式展开的方法, 对选定的背景光谱点进行拟合, 并将拟合结果从原始光谱中扣除, 可以获得较为纯净的光谱数据。对M个点的光谱数据S进行4阶多项式拟合的表达式为

$f = a_{0} + a_{1} i + a_{2} i^{2} + a_{3} i^{3} + a_{4} i^{4}$ (5)

式(5)中, a_p(p=0, 1, 2, 3, 4)为多项式的系数; i为光谱的通道地址; f为多项式拟合的光谱值。

计算原光谱数据点与拟合数据点之间的距离平方和

$S_{d}^{2}=\displaystyle\sum_{i=1}^{M}\left[S(i)-f\left(i, a_{0}, a_{1}, \cdots, a_{4}\right)\right]^{2}$(6)

式(6)中, S为原光谱数据, M为光谱的总通道地址数。

Mor+DIPF算法的实现步骤如下:

1) 输入原始光谱数据S, 设置窗口半宽为L_s, 基于形态学算法求侵蚀操作E(S_i)、膨胀操作D(S_i)、开运算O(S_i)和P运算。

2) 通过P运算计算得出的光谱背景信号作为新的待拟合光谱信号y₀。

3) 基于导数迭代多项式拟合算法对y₀进行拟合, 得到最终的光谱背景y_n。

4) 将y_n从原始光谱数据S扣除即可得到本底信号校正后的纯净光谱信号。

1.2 基于APU-PSO-EM-GMM的光谱重叠峰分解

1.2.1 基于EM算法的GMM参数初步解析

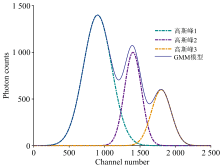
经过光谱数据本底扣除后, XRF光谱中的特征峰可视为一个高斯峰, 重叠峰相当于多个高斯峰叠加构成的高斯混合模型(GMM), 如图2所示。因此, 重叠峰解析实质上是对GMM模型的解析。只要能够准确估计GMM模型的参数, 便可完成重叠峰的解析。

	Figure Option View Download New Window
	图2 GMM模型示意图Fig.2 Schematic diagram of the GMM model

由于事先不知道XRF光谱重叠峰中的N个数据x_N(每个通道数对应的特征X射线强度值)来自某一个高斯特征峰的概率, 而只能得到最终的观测数据, 所以重叠峰数据是含有隐变量的, 适合用EM算法来求解参数, 求解步骤如下:

1) GMM中初始参数θ 由三部分组成: 包括各个特征峰的峰位μ _m, 方差 $σ_{m}^{2}$ 和各个特征峰占总峰面积的权重π _m。假设重叠峰由k个高斯分布组成, 即θ =[μ ₁, μ ₂, …, μ _k, $σ_{1}^{2}$ , $σ_{2}^{2}$ , …, $σ_{k}^{2}$ , π ₁, π ₂, …, π _k]。

2) 引入隐变量Z

$Z = [Z_{1}, \dots, Z_{i}, \dots, Z_{N}]$ (7)

式(7)中, Z_i=[Z_i₁, …Z_im, …, Z_ik], Z_im表示第i个光谱数据点属于第m个高斯特征峰的概率, 每一个数据点来源于k个高斯特征峰的概率总和为1, 即$\displaystyle\sum_{m=1}^{k} Z_{i m}=1$。

3) 隐变量Z可以指示重叠峰数据x_N属于哪一个高斯特征峰, 这样就能将观测不完整数据转化为完整数据, 用Y表示完整数据[x_N, Z], 则完整数据的似然函数可表示为

$P(Y \mid \theta)=\displaystyle\prod_{m=1}^{k} \displaystyle\prod_{i=1}^{N}\left[\pi_{m} N\left(x_{i} \mid \mu_{m}, \sigma_{m}^{2}\right)\right]^{z_{i m}}$(8)

完整数据的对数似然函数为

$\log P(Y \mid \theta)=\displaystyle\sum_{m=1}^{k} \displaystyle\sum_{i=1}^{N} z_{i m}\left(\log \pi_{m}+\log N\left(x_{i} \mid \mu_{m}, \sigma_{m}^{2}\right)\right.$(9)

4) 在E-step中, 目标代价函数可以表示为

$\begin{array}{c}Q\left(\theta, \theta^{t}\right)=\displaystyle\sum_{m=1}^{k} \sum_{i=1}^{N}\left(\log \pi_{m}+\right. \left.\log N\left(x_{i} \mid \mu_{m}, \sigma_{m}^{2}\right)\right) P\left(z_{i m} \mid x_{i}, \theta^{t}\right) \end{array}$(10)

式(10)中, θ ^t表示第t次迭代估计的参数集。为了得到代价函数(10), 需要计算隐变量的后验概率P(z_im|x_i, θ ^t)。

5) 在上一次迭代参数下, 每个样本数据点x_i属于第m个高斯特征峰的后验概率r_im可以表示为

$r_{i m}=P\left(z_{i m} \mid x_{i}, \theta^{t}\right)=\frac{\pi_{m}^{t} ~~~N\left(x_{i} \mid ~~\mu_{m}^{t}, \left(\sigma_{m}^{2}~~\right)^{t}\right)}{\displaystyle\sum_{j=1}^{k} ~~\pi_{j}^{t}~~ N\left(x_{i} \mid ~~\mu_{j}^{t}, \left(\sigma_{j}^{2}~~\right)^{t}\right)~~~}$(11)

6) 在M-step中, 最大化目标代价函数更新GMM参数, 这一过程可定义为

$θ_{t + 1} = argma x Q (θ, θ^{t})$ (12)

将代价函数对GMM参数求偏导, 并令导数为0, 可得到各个参数的新一轮迭代值, 从而完成M步。每个高斯特征峰的峰位μ _m, 方差 $σ_{m}^{2}$ 和高斯特征峰占总峰面积的权重π _m的迭代估计公式可分别表示为

$\mu_{m}^{t+1}=\frac{\displaystyle\sum_{i=1}^{N} r_{i m} x_{i}}{\displaystyle\sum_{i=1}^{N} r_{i m}}, m=1, 2, \cdots, k$(13)

$\left(\sigma_{m}^{2}\right)^{t+1}=\frac{\displaystyle\sum_{i=1}^{N} r_{i m}\left(x_{i}-\mu_{m}\right)^{2}}{\displaystyle\sum_{i=1}^{N} r_{i m}}, m=1, 2, \cdots, k$(14)

$\pi_{m}=\frac{1}{N} \displaystyle\sum_{i=1}^{N} r_{i m}, m=1, 2, \cdots, k$(15)

在实际应用中, EM算法是估计高斯混合模型参数的常见方法, 但易受初始参数影响, 易陷入局部最优, 影响重叠峰解析准确性。因此, 为了提高重叠峰解析的准确性, 还需在EM算法解析重叠峰的初始值参数θ 上做一定的优化。

1.2.2 基于自适应参数更新策略的粒子群优化算法

粒子群优化(PSO)算法因收敛快、参数少, 适用于重叠峰参数的全局优化, 但传统PSO易早熟收敛, 影响优化效果。为了提高PSO算法的局部搜索能力和全局搜索能力, 本文在惯性权重w、个体学习因子c₁和社会学习因子c₂三个参数上提出自适应更新策略。基于自适应参数更新策略的粒子群优化算法实现过程如下所示:

1) 设置算法相关参数。初始化粒子的种群规模P=50; 粒子搜索空间的维度D=3k; 即高斯特征重叠峰的参数θ =[μ ₁, μ ₂, …, μ _k, $σ_{1}^{2}$ , $σ_{2}^{2}$ , …, $σ_{k}^{2}$ , π ₁, π ₂, …, π _k], 每个粒子的位置代表特征峰的峰位置、方差以及各个子峰占总峰面积的权重;

2) 通过随机初始化生成粒子位置和粒子速度, 并且根据式(9)的对数似然目标函数计算出每个粒子的适应度值。将初始化的粒子位置作为个体历史最优值p_best, 将每个粒子适应度值进行排序, 选择最大适应度值所对应的粒子位置作为初始全局最优位置g_best。

3) 自适应调整惯性权重w:

$w=\left\{\begin{array}{ll} w_{\min }-\frac{\left(w_{\max }-w_{\min }~~\right) \times\left(f-f_{\min }~\right)~~~}{\left(f_{\mathrm{avg}}-f_{\min }\right)}, & f \leqslant f_{\mathrm{avg}} \\ w_{\max }, & f> f_{\mathrm{avg}} \end{array}\right.$(16)

式(16)中, f表示当前粒子的适应度值, f_avg表示粒子群的平均适应度值, f_min表示粒子群的最小适应度值。

4) 个体学习因子c₁和社会学习因子c₂自适应更新

$c_{1} = c_{1 \max} - (c_{1 \max} - c_{1 \min}) \times (\frac{iter - 1}{Max_iter - 1})$ (17)

$c_{2} = c_{2 \min} + (c_{2 \max} - c_{2 \min}) \times (\frac{iter - 1}{Max_iter - 1})$ (18)

式中, iter为当前迭代的次数, Max_iter为初始化设置的最大迭代次数。

5) 更新粒子的位置和速度

$V_{i}^{(iter + 1)} = w V_{i}^{iter} + c_{1} r_{1} (P_{i}^{iter} - X_{i}^{iter}) + c_{2} r_{2} (P_{g}^{iter} - X_{i}^{iter})$ (19)

$X_{i}^{iter + 1} = X_{i}^{iter} + V_{i}^{(iter + 1)}$ (20)

式中, $V_{i}^{(iter + 1)}$ 为第i个粒子在第iter+1次迭代次数的速度; $X_{i}^{iter + 1}$ 为第i个粒子在第iter+1次迭代次数的位置; $P_{i}^{iter}$ 为第i个粒子到第iter次迭代次数为止搜索到的个体最优位置; $P_{g}^{iter}$ 为所有粒子到第iter次迭代次数为止搜索到的全局最优位置; r₁和r₂为[0, 1]中的随机数。

6) 计算更新后粒子的适应度值, 并且更新个体最优位置p_best和全局最优位置g_best。

7) 当迭代次数达到设定的最大迭代次数时, 算法停止。输出全局最优的粒子位置g_best, 即XRF光谱重叠峰中各个特征峰的峰位μ _m、方差 $σ_{m}^{2}$ 和子峰占总峰面积的权重π _m。

1.2.3 APU-PSO-EM-GMM算法描述

表1 APU-PSO-EM-GMM光谱重叠法分解算法伪代码 Table 1 Pseudocode for the APU-PSO-EM-GMM spectral overlap decomposition algorithm

输入可观测数据集: XRF光谱重叠峰中的N个数据x_N(N个通道数对应的特征X射线强度值)
初始参数设置: 粒子种群规模P=50; 粒子搜索空间维度D=3k, 即高斯特征重叠峰的解析参数θ =[μ ₁, μ ₂, …, μ _k, $σ_{1}^{2}$ , $σ_{2}^{2}$ , …, $σ_{k}^{2}$ , π ₁, π ₂, …, π _k]; 最大迭代次数Max_iter=50; w_max=0.9; w_min=0.4; c_1max=c_2max=2; c_1min=c_2min=2; V_max=5; V_min=5。
1. 随机初始化生成各个粒子的位置和速度, 并利用式(9)计算每个粒子的适应度值。将初始化粒子位置作为初始个体历史最优值P_best, 对每个粒子适应度值进行排序, 选择最大适应度值所对应的粒子位置作为初始全局最优位置g_best。设置APU-PSO算法的初始迭代次数iter=1;
2. While iter≤ Max_iter, Do
3. 基于式(16)计算惯性权重w;
4. 基于式(17)计算个体学习因子c₁;
5. 基于式(18)计算社会学习因子c₂;
6. For i=1 to P, Do
7. 基于式(19)更新每个粒子的速度;
8. 基于式(20)更新每个粒子的位置;
9. 基于式(9)计算粒子位置更新后的适应度值f( $X_{i}^{iter}$ );
10. 更新个体历史最优位置P_best;
11. If f(P_best)< f( $X_{i}^{iter}$ ) then
12. P_best= $X_{i}^{iter}$ ;
13. End if
14. 更新全局最优位置g_best;
15. If f(g_best)< f( $X_{i}^{iter}$ ) then
16. g_best= $X_{i}^{iter}$ ;
17. End if
18. End
19. End while
20. g_best: $\dot{θ}$ = [ ${\dot{μ}}_{1}$ , ${\dot{μ}}_{2}$ , …, ${\dot{μ}}_{k}$ , ( ${\dot{σ}}_{1}^{2}$ ), ( ${\dot{σ}}_{2}^{2}$ ), …, ( ${\dot{σ}}_{k}^{2}$ ), ${\dot{π}}_{1}$ , ${\dot{π}}_{2}$ , …, ${\dot{π}}_{k}$ ]
21. 由APU-PSO优化算法得到EM估计GMM模型的最优初始参数值θ ;
22. 设定EM算法的初始迭代次数iter=1;
23. While Iter≤ Max_iter, Do
24. E-step: 构建目标代价函数
25. 基于式(11)计算隐变量的后验概率P(z_im\|x_i, θ ^iter);
26. 基于式(10)构建目标代价函数Q(θ , θ ^iter);
27. M-step: 更新各参数估计
28. 根据迭代式(13)估计高斯特征峰的峰位μ _m;
29. 根据迭代式(14)估计高斯特征峰的方差 $σ_{m}^{2}$ ;
30. 根据迭代式(15)估计高斯特征峰占总峰面积的权重π _m;
31. 更新迭代次数Iter=Iter+1, 且获得θ ^Iter={ $μ_{m}^{Iter}$ , ( $σ_{m}^{2}$ )^Iter, $π_{m}^{Iter}$ } ;
32. End While
输出: 最优高斯特征峰解析参数集θ ^* =[ $μ_{1}^{}$ , $μ_{2}^{}$ , …, $μ_{k}^{}$ , ( $σ_{1}^{2}$ )^, ( $σ_{2}^{2}$ )^, …, ( $σ_{k}^{2}$ )^, $π_{1}^{}$ , $π_{2}^{}$ , …, $π_{k}^{*}$ ]。

表1 APU-PSO-EM-GMM光谱重叠法分解算法伪代码 Table 1 Pseudocode for the APU-PSO-EM-GMM spectral overlap decomposition algorithm

2 基于Transformer-BiLSTM实现钛铁矿品位检测

2.1 整体策略

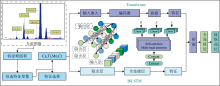
为应对传统基体效应校正方法在钛铁矿品位定量分析中存在的精度有限、效率偏低等问题, 本文提出一种融合Transformer与双向长短期记忆网络(BiLSTM)的定量分析建模方法。该模型利用Transformer架构强大的全局特征提取能力, 充分挖掘历史工况变量与实时监测数据间的长距离依赖关系; 同时引入BiLSTM网络结构, 有效增强模型对时间序列双向动态特征的学习能力。通过对多源工艺变量的动态建模, 该模型能够深度提取影响品位波动的关键特征, 实现对钛铁矿品位的定量分析。图3展示了XRF 品位检测系统结构框架。

	Figure Option View Download New Window
	图3 XRF的钛铁矿品位检测方法结构图Fig.3 Structural diagram of XRF titanium iron ore grade detection method

2.2 BiLSTM双向长短期记忆网络基本原理

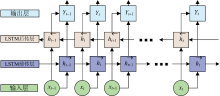
双向长短期记忆网络(BiLSTM)是一种改进型循环神经网络, 其核心原理在于通过同时学习时间序列的正向和反向特征, 提升对时序数据的建模能力。 BiLSTM由两个独立的LSTM层构成: 一个从前向后处理输入序列(前向LSTM), 另一个从后向前处理输入序列(后向LSTM)。前向LSTM捕捉序列从过去到当前的动态特征, 而后向LSTM则捕捉从未来到当前的动态特征。通过并行运行这两个LSTM层, BiLSTM 能够分别提取序列的前向和后向上下文信息, 将结果进行融合, 从而全面捕捉序列中的全局特征和依赖关系。 LSTM和BiLSTM的基本结构如图4和图5所示。

	Figure Option View Download New Window
	图4 LSTM的基本机构Fig.4 Basic structure of LSTM

	Figure Option View Download New Window
	图5 BiLSTM的基本机构Fig.5 Basic structure of BiLSTM

2.3 Transformer基本原理

Transformer架构由多头自注意力机制与前馈神经网络构成, 是一种具备强全局建模能力的序列学习方法。如图6所示, 输入特征首先通过线性变换映射为查询向量(Q)、键向量(K)和值向量(V), 通过计算Q与K的点积得到位置间的相关性, 并以此为权重加权求和V, 实现对各输入位置间全局依赖关系的建模。多头机制允许模型在不同子空间中并行建模注意力特征, 增强特征表达能力。编码器每个子模块均采用残差连接与LayerNorm归一化操作以提高训练稳定性。

	Figure Option View Download New Window
	图6 Transformer编码器层结构示意图Fig.6 Schematic diagram of a Transformer encoder layer

3 实验分析与工业应用

3.1 实测钛铁矿样本光谱的结果分析

为了验证本文所提出的Mor+DIPF算法在模拟高斯光谱中本底扣除的有效性, 分别与XRF中常用的两种本底扣除方法: 自适应迭代重加权惩罚最小二乘法(airPLS)、自适应平滑约束最小二乘法(ASLS)以及多项式拟合法(PF)、迭代多项式拟合法(IPF)、形态学方法(Mor)进行对比实验。为了评估六种不同算法对不同形状光谱的校正效果, 采用均方根误差(RMSE)、平均相对误差(MAE)和决定系数(R²)三个性能指标来衡量校正后基线和模拟基线之间的误差和相关性, 三种评价指标的计算如式(21)— 式(23)所示, 结果如表2— 表4所示。

$\mathrm{RMSE}=\sqrt{\frac{\displaystyle\sum_{i=1}^{M}\left(z_{i}-t_{i}\right)^{2}}{M}}$(21)

$\mathrm{MAE}=\frac{1}{M} \displaystyle\sum_{i=1}^{M}\left|z_{i}-t_{i}\right|$(22)

$R^{2}=1-\frac{\displaystyle\sum_{i=1}^{M}\left(z_{i}-t_{i}\right)^{2}}{\displaystyle\sum_{i=1}^{M}\left(t_{i}-\bar{t}\right)^{2}}$(23)

$\mathrm{MAPE}=\frac{1}{M} \displaystyle\sum_{i=1}^{M}\left|\frac{z_{i}-t_{i}}{t_{i}}\right| \times 100 \% $(24)

$\mathrm{MSE}=\frac{1}{M} \displaystyle\sum_{i=1}^{M}\left(z_{i}-t_{i}\right)^{2}$(25)

表2 六种本底扣除算法在四种不同基线下的RMSE Table 2 RMSE of six background subtraction algorithms under four different baselines

表3 六种本底扣除算法在四种不同基线下的MAE Table 3 MAE of six background subtraction algorithms under four different baselines

表4 六种本底扣除算法在四种不同基线下的R²(%) Table 4 R² of six background subtraction algorithms under four different baselines (%)

对表2、表3和表4数据分析, 六种算法在处理四种不同的光谱时表现出不同的性能特征。本研究提出的Mor+DIPF算法在性能上优于IPF、 DIPF、 airPLS、 ASLS和Mor算法。

为了验证本文所提出的APU-PSO-EM-GMM算法在重叠峰解析上的有效性, 分别与XRF中常用的三种重叠峰分解算法: 曲线拟合法、高斯锐化法、离散小波变换法(DWT)以及三种优化算法: 基于和声搜索优化EM算法(HS-EM-GMM)、基于蝙蝠行为优化EM算法(BA-EM-GMM)和基于麻雀搜索优化EM算法(SSA-EM-GMM)进行对比实验。图7为七种对比算法在普通重叠峰、肩部重叠峰和多重叠峰上的拟合结果。从图中可以看出, 曲线拟合、高斯锐化法和DWT算法在拟合的整体趋势上表现较差, 尤其在峰值位置上存在较大的偏差。相比之下, SSA-EM-GMM、 BA-EM-GMM和HS-EM-GMM这三种基于EM-GMM的优化算法在捕捉峰值和细节方面表现较为出色。而本文提出的APU-PSO-EM-GMM算法在整体拟合效果上最为接近模拟重叠峰, 显示出其在处理重叠峰时具有显著的优势。

	Figure Option View Download New Window
	图7 七种对比算法在普通重叠峰, 肩部重叠峰和多重叠峰下的拟合结果Fig.7 Fitting results of seven comparison algorithms under ordinary overlapping peaks, shoulder overlapping and multiple overlapping peaks

3.2 钛铁矿品位定量分析的结果评价

在本文中, 采用实际工业现场采集的钛铁矿样本数据开展实验。通过在光谱分析软件中加载不同品位的钛铁矿光谱, 对特征峰的变化趋势进行观察, 并分析影响铁元素光子计数变化的关键特征变量。实验结果显示, 钛铁矿与铁矿石之间的光谱信号存在显著干涉现象。具体而言, Mn与Fe之间存在光谱线重叠, 而Cr元素则对Fe、 Ca和Ti的特征X射线表现出明显吸收效应。作为高原子序数元素, Cr 具备更强的 X 射线吸收能力, 尤其对Fe-Kα (约 6.40 keV)具有明显的吸收作用, 进而导致目标元素Fe的光子计数显著减少。综合光谱分析结果可见, 样品中存在四种主要共存元素: Ca、 Ti、 Mn和Cr, 它们均对Fe元素的荧光强度产生干扰影响。数据集共有41组数据, 按照训练集与测试集=8∶ 2进行划分。为避免特征间量纲不一致带来的影响, 本文采用最大-最小归一化方法对数据进行处理, 将各特征值线性映射至[0, 1]区间。令X=[I_Ca, I_Ti, I_Mn, I_Cr, I_Fe], X为41× 5阶矩阵, 其中I_{(· )}表示各元素的X射线荧光强度值, 通过式(26) 进行数据处理

$X^{*}=\frac{X-\min (X)}{\max (X)-\min (X)~~~~}$(26)

为了验证本文所提出的Transformer-BiLSTM算法在钛铁矿品位定量分析的性能, 与常用的四种算法: 支持向量机(SVM), Transformer, Transformer融合LSTM进行对比实验。本文采用了MAE、 RMSE和R²作为模型评价指标。表5 给出四种算法对钛铁矿品位定量分析的评价量化指标, 可以看出本文所提出的Transformer-BiLSTM的平均绝对误差为0.217 2、均方根误差为0.280 7, 为四种算法当中最小。决定系数为99.716 1%, 更逼近理想值1。

表5 模型检测结果评价 Table 5 Evaluation of model detection results

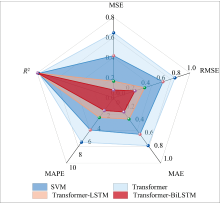
图8展示了四种模型(SVM、 Transformer、 Transformer-LSTM、 Transformer-BiLSTM)在五个关键性能指标(MSE、 RMSE、 MAE、 MAPE、 R²)上的对比结果。其中, MSE与RMSE最低, 说明其在拟合能力上最为精准; MAE与MAPE最小, 表明模型在不同样本下的泛化误差波动最小; R²为0.997 1, 接近于理想值1, 反映了该模型对真实数据的拟合度极高。 Transformer-BiLSTM模型在定量分析的精度、稳定性与泛化能力方面均达到最优状态。

	Figure Option View Download New Window
	图8 四种估计模型的评估指标雷达图Fig.8 Radar chart of evaluation indicators for four estimation models

3.3 工业系统设计与实际应用

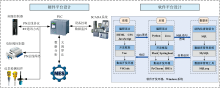
本系统软硬件平台如图9所示, 其中硬件平台采用汇川SV660F伺服控制器与西门子PLC通过PN总线及RT通讯实现高精度控制; 气控系统通过PN总线阀岛减少布线、提高通讯实时性; 现场仪表采用继电器输出, 增强抗干扰能力。 MES系统通过OPC-UA协议与PLC通讯, 实现XRF分析数据的实时传输与管理优化; SCADA系统采用WINCC 7.5 SP2, 通过S7协议与PLC通信, 实现设备监控与数据采集。软件平台如图9所示, 基于Windows系统, 前端采用Vue框架, 后端采用Spring Boot与Flask, 数据库使用MySQL, 整体架构灵活高效。该系统已在沈阳某选矿厂应用6个月以上, 图10展示了钛铁矿品位实时检测模块, 可动态显示检测与人工化验结果。表6数据显示, 系统在设定3%相对误差范围内的估计合格率均超90%, 验证了系统在工业现场的实用性与准确性。

	Figure Option View Download New Window
	图9 软硬件平台设计Fig.9 Hardwareand software platform design

	Figure Option View Download New Window
	图10 钛铁矿品位实时与历史检测模块Fig.10 Real-timeand historical detection module for titaniferous iron ore grade

表6 投运六个月余的钛铁矿品位估计误差分析 Table 6 Error analysis of titanium iron ore grade estimation after more than six months of operation

4 结论

针对XRF光谱分析中普遍存在的本底干扰与谱峰重叠问题, 提出了两种算法优化方式。首先, 在EDXRF光谱仪获取数据的过程中, 由于外界干扰、 X射线与样品之间的相互作用等因素造成噪声和背景信号的产生, 提出一种基于形态学与导数迭代多项式拟合的本底扣除方法, 确保精确获取目标元素XRF光谱谱峰及其净峰面积; 进一步将获得的净荧光光谱数据输入到EM算法中进行重叠峰参数的初步解析, 以得到各个特征峰的峰位、方差和权重。其次, 针对EM算法对初始参数的选择较为敏感, 易陷入局部最优的缺点以及标准粒子群优化算法存在早熟收敛问题, 提出一种基于自适应参数更新策略的粒子群优化算法, 从惯性权重w、个体学习因子c₁和社会学习因子c₂三个参数上进行改进, 从而获得更为精确的解析结果。最后, 在此基础上构建了Transformer-BiLSTM的钛铁矿品位检测方法, 实现了高精度、轻量化的在线检测建模, 为传统化学分析方法提供了高效可行的替代方案。

参考文献

文献列表

[1]	FAN Song-mei, SHA Jing-hua, YAN Jing-jing, et al(范松梅, 沙景华, 闫晶晶, 等). Resources Science(资源科学), 2018, 40(3): 507. [本文引用:1]
[2]	Zhao J S, Ni K, Su Y P, et al. Construction and Building Materials, 2021, 286: 122968. [本文引用:1]
[3]	Zhou Y L, Jiang X, Wang X A, et al. Metallurgical and Materials Transactions B, 2022, 53(6): 4075. [本文引用:1]
[4]	LU Dan(芦丹). Mining Research and Development(矿业研究与开发), 2019, 39(12): 177. [本文引用:1]
[5]	AN Xiao-qiang, ZHOU Chang-chun, LI Zhen, et al(安小强, 周长春, 李振, 等). Light Metals(轻金属), 2008, (11): 52. [本文引用:1]
[6]	ZHANG Yang, ZHENG Shi-li, WANG Xiao-hui, et al(张洋, 郑诗礼, 王晓辉, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2010, 30(1): 251. [本文引用:1]
[7]	WANG Min-lei(王敏蕾). Non-ferrous Mining and Metallurgy(有色矿冶), 2007, 23(4): 88. [本文引用:1]
[8]	WANG Yong-bao(王永保). Chemical Enterprise Management(化工管理), 2020, (32): 69. [本文引用:1]
[9]	Shard A G, Wright L, Minelli C. Biointerphases, 2018, 13(6): 061002. [本文引用:1]
[10]	Tekin Z, Unutkan T, Erulas F, et al. Food Chemistry, 2020, 310: 125825. [本文引用:1]
[11]	Nakano H, Komatani S, Matsuyama T, et al. Analytical Sciences, 2021, 37(10): 1447. [本文引用:1]
[12]	Singh V, Sharma N. X-ray Spectrometry, 2022, 51(3): 304. [本文引用:1]
[13]	Lagerstrom M, Ytreberg E. Talanta, 2021, 223(2): 121820. [本文引用:1]
[14]	Ma Q, Pollard A M, Jiang J, et al. Archaeometry, 2021, 63(1): 194. [本文引用:1]
[15]	Li Y, Wang Q, Sun N, et al. Spectroscopy Letters, 2013, 46(7): 507. [本文引用:1]
[16]	Yan Y, Zhao X, Zhang D. Medicinal Plant, 2014, 5(6): 33. [本文引用:1]
[17]	HU Jin-song, BAO Ji-long, ZHOU Fang-hao, et al(胡劲松, 鲍吉龙, 周方浩, 等). Chinese Journal of Analytical Chemistry(分析化学), 2006, 34(3): 418. [本文引用:1]
[18]	Yang X Y, Zhang C C, Wang C Y, et al. Ultrasonics, 2018, 91: 231. [本文引用:1]

2018

0.0

... 引言钢铁制品作为国民经济和社会发展的重要基础材料产业, 在社会生产和人民生活中占据着不可或缺的地位^[1] ...

2021

0.0

... 相关统计数据显示, 全球粗钢年产量已突破18亿吨, 其中中国粗钢产量约为9亿吨, 产量占比接近50%^[2] ...

2022

0.0

... 尽管我国铁矿石储量较为丰富, 但主要以低品位矿石为主, 且矿石类型复杂多样, 导致开采难度大、选矿成本高, 同时面临能耗高和生产效率低等技术难题, 这些因素制约了钢铁工业的高质量发展^[3,4] ...

2019

0.0

2008

0.0

... 目前, 针对铁矿石品位的定量分析研究方案较为丰富, 多集中于传统化学分析方法, 包括ICP-AES法、 EDTA滴定法、稳健统计法以及碘氟法等^[5,6,7,8] ...

2010

0.0

... 目前, 针对铁矿石品位的定量分析研究方案较为丰富, 多集中于传统化学分析方法, 包括ICP-AES法、 EDTA滴定法、稳健统计法以及碘氟法等^[5,6,7,8] ...

2007

0.0

... 目前, 针对铁矿石品位的定量分析研究方案较为丰富, 多集中于传统化学分析方法, 包括ICP-AES法、 EDTA滴定法、稳健统计法以及碘氟法等^[5,6,7,8] ...

2020

0.0

... 目前, 针对铁矿石品位的定量分析研究方案较为丰富, 多集中于传统化学分析方法, 包括ICP-AES法、 EDTA滴定法、稳健统计法以及碘氟法等^[5,6,7,8] ...

2018

0.0

... 近年来, 基于光谱的分析方法成为研究热点, 其中包括原子吸收光谱法、原子荧光光谱法和X射线荧光光谱法等^[9,10] ...

2020

0.0

... 近年来, 基于光谱的分析方法成为研究热点, 其中包括原子吸收光谱法、原子荧光光谱法和X射线荧光光谱法等^[9,10] ...

2021

0.0

... 在这其中, X射线荧光光谱法(X-ray fluorescence, XRF)以其快速的检测速度、较低的分析成本和广泛的适用元素范围等优点, 成为矿石元素分析的关键工具之一^[11], 被广泛应用于环境科学、化学以及生物学等多个学科领域, 并在一定程度上取代了传统的化学分析方法^[12,13,14] ...

2022

0.0

2021

0.0

2021

0.0

2013

0.0

... 其次是在谱线特征峰重叠问题上, 研究者常采用的方法包括曲线拟合法^[15]、导数法^[16]、小波变换法^[17], 这些方法在处理谱线重叠问题上得到了广泛应用 ...

2014

0.0

2006

0.0

2018

0.0

... 本文从元启发式算法^[18]入手, 提出基于自适应参数更新策略的粒子群优化算法, 结合高斯混合模型, 采用EM算法对重叠峰进行解析 ...