不断演化的太阳磁场产生太阳大气活动, 如黑子、 日珥、 耀斑和日冕物质抛射^{[1, 2, 3]}, 引发严重的空间天气, 对人类的生产生活产生了严重影响。 因此, 需要建立精确的太阳大气物理模型并对太阳活动事件进行实时监测和预报^{[4, 5]}。 研究太阳大气活动的物理过程需要识别太阳大气活动精细结构的热力学参数如温度和速度等, 而具有高光谱分辨率的光栅光谱仪是实现这一目标的重要仪器之一。 其较宽的自由光谱范围可以同时对光球层和色球层的太阳大气活动进行同时观测^[6]。 通过光谱标定得到准确的光谱信息, 通过拼接狭缝像可以获得大视场图像^{[7, 8]}。 然而, 由于受到光学系统的成像噪声和光学像差影响, 探测到狭缝图像质量显著退化。

自适应光学(AO)可以实时补偿由大气湍流引起的光学像差^{[9, 10, 11]}。 因此狭缝图像的质量很大程度上取决于AO系统的校正性能^{[12, 13]}。 与一般的光学系统不同, 光栅光谱仪的狭缝足够窄, 这会在一定程度上过滤波前像差, 传统AO方法不能直接应用于校正光栅光谱仪的光学像差^[14]。 为了解决上述问题, 提出了基于AO的光栅成像光谱仪的像差校正方法^{[15, 16]}。 此外, 还提出了一种基于狭缝滤波灵敏度的自适应光学校正方法^[17]。 然而传统的AO性能受限于等晕角范围和系统复杂性。

除了AO校正方法外, 事后图像重建技术也可以去除大气湍流的影响, 获得高质量的大视场图像^[18]。 由于存在光学像差和噪声, 降低了图像复原算法的有效性和准确性^{[19, 20]}, 这对基于深度学习的图像分类结果尤其不利^[21]。 此外, 噪声会在像素强度中引入随机变化, 降低对比度, 并可能产生虚假结构或伪影。 这使得恢复算法难以准确区分真实图像特征和由噪声引起的变异特征^{[22, 23, 24]}。 虽然提出了一些基于图像先验、 PSF先验的去模糊方法^{[25, 26, 27]}, 但PSF的估计误差不可避免, 可能会产生伪影^[28]。 最近, 有许多稳定性好的图像去模糊方法可用于恢复模糊图像, 如Lucy-Richardson(LR)反卷积、 ForWaRD、 LR²A以及深度学习方法^[29]。 在这些去模糊方法中, LR²A是一种新颖的计算重构方法, 由Lucy-Richardson算法(LRA)与非线性重构(NLR)算法构成^[30]。 多项研究表明, LR²A的性能明显优于LRA和NLR^[31]。 这些研究集中在如何在提高图像清晰度和抑制噪声之间做出适当的权衡。 其中, LRA因其简单和对噪声的高度容忍性, 因而在天体物理或显微成像中得到广泛应用。 但是当光学像差较大时, LRA通常会产生明显的振铃伪影^[32]。 此外, LRA的一个重要缺点是它不会收敛到有意义的解, 因为噪声在少量迭代后会被放大。 通常采用正则化约束可以降低噪声的敏感性, 从而获得更优的结果。

与传统光学系统不同, 狭缝滤波会导致图像的部分结构或细节丢失, 并且相位发生变化, 使得狭缝图像与原始相位不一致。 常用去模糊方法在这种情况下效率低下甚至失效。 因此, 在进行狭缝图像复原时, 必须对滤波后的相位施加正则化约束, 这要求我们具备滤波后相位的先验知识, 以便提出有效的正则化约束方法。

在本文中, 我们提出了一种新方法, 通过重构滤波后的相位并采用LR2A计算成像算法, 实现狭缝图像的高质量复原, 有效消除光学像差和图像噪声对光谱仪光谱和空间分辨率的影响。 据我们所知, 这是少数几种解决狭缝图像复原问题的方法之一, 适用于高光谱分辨率光谱仪技术的光学像差和低信噪比场景, 并在宽带乃至白光条件下表现出色。 该方法能够准确重建狭缝图像, 实现接近衍射极限的成像性展具有重要意义。

图像退化过程可以通过式(1)表示

O(x, y)=I(x, y)⊗PSF(x, y)+n(x, y)(1)

式(1)中, O(x, y) 表示模糊后的图像, I(x, y)是清晰的原始图像, PSF(x, y)是系统的点扩散函数, n(x, y)是噪声。 符号“ 􀱋” 表示卷积算子。

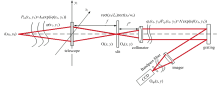
成像光栅光谱仪是望远镜的一个重要组成部分, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 成像光栅光谱仪的示意图Fig.1 Schematic diagram of the imaging grating spectrometer

根据傅里叶光学原理, 点光源的强度分布图像O(x₂, y₂)可以表示为

O(x2, y2)=PSFta(x2, y2)=F{A0eiφ(x1, y1)}2(2)

式(2)中, PSF_ta是望远镜光学系统和大气湍流的点扩散函数, F{}表示傅里叶变换操作符, φ (x₁, y₁)是由望远镜和大气湍流引起的等效波前像差。

与一般光学系统不同, 光栅光谱仪的狭缝非常窄(例如, 在太阳观测中通常为10~100 μ m)。 因此, 波前像差的高频部分会被狭缝过滤掉。 经过狭缝后的点扩散函数PSF_ta(x₂, y₂)可以表示为

$\begin{aligned} O\left(x_{2}, y_{2}\right) & =\operatorname{PSF}_{\mathrm{ta}}\left(x_{2}, y_{2}\right) \operatorname{rect}^{2}\left(\frac{x_{2}}{w_{\mathrm{s}}}\right) \operatorname{rect}^{2}\left(\frac{y_{2}}{L_{\mathrm{s}}}\right) \\ & =\left|F\left\{A_{0} \mathrm{e}^{i \varphi\left(x_{1}, y_{1}\right)}\right\}\right|^{2} \operatorname{rect}^{2}\left(\frac{x_{2}}{w_{\mathrm{s}}}\right) \operatorname{rect}^{2}\left(\frac{y_{2}}{L_{\mathrm{s}}}\right) \end{aligned}$(3)

式(3)中, w_s和L_s分别是狭缝的宽度和长度, rect是矩形函数, 如式(4)和式(5)所示

rectxws=1, -0.5ws≤x≤-0.5ws0, otherwise(4)

rectyLs=1, -0.5Ls≤x≤-0.5Ls0, otherwise(5)

在光谱仪的焦平面处, 点扩散函数PSF(x, y)可以表示为

PSF(x, y)=PSFs(x, y)⊗PSFsp(x, y)(6)

式(6)中, PSF_s(x, y)是PSF_s(x₂, y₂)的图像, PSF_sp(x, y)是成像光栅光谱仪的点扩散函数, 而φ '(x₃, y₃)是光栅光谱仪的等效波前像差。 通过精确调整光学系统可以消除PSF_sp的影响, 在本文中将不再讨论φ '(x₃, y₃)的影响。 需要注意的是, 上述描述中的PSF_sp影响可以通过精确校准光学系统来消除, 因此未进一步讨论φ '的影响。 方程(6)的最简形式由式(7)给出

PSF(x, y)=PSFs(x, y)=F{A0exp(iφ(x1, y1))}2(7)

式(7)中, φ _s(x, y)是滤波狭缝后的光学像差。

假设φ (x, y)是不受滤波狭缝影响并通过哈特曼-夏克波前传感器(HS WFS)检测到的光学像差。 光学系统的近场函数和远场函数可以分别由E_nf(x, y)和E_far(x, y)表示。 近场函数E_nf(x, y)可以表达为

Enf(x, y)=pupil(x, y)×exp(iφ(x, y))(8)

式(8)中, pupil(x, y)表示一个光瞳孔径函数, 它可以表达为

$\operatorname{pupil}(x, y)=\left\{\begin{array}{ll} 1, & \sqrt{x^{2}+y^{2}} \leqslant r \\ 0, & \text { otherwise } \end{array}\right.$(9)

式(9)中, r表示孔径的半径。

远场函数E_far(x, y)可以表示为

Efar(x, y)=F{Enf(x, y)}×recxws×recyLs(10)

由于狭缝过滤效应, 波前像差的部分会被过滤掉, 因此需要重建滤波后的相位。 近场函数E_nf-s(x, y)可以通过式(11)计算

Enf-s(x, y)=F{Efar(x, y)}(11)

其中, 下标s表示狭缝。

滤波后的相位可以表示为

$\begin{array}{l} \operatorname{phase}_{\mathrm{s}}(x, y)= \\ \text { angle }\left\{E_{n f-\mathrm{s}}(x, y)\right\} \times \text { angle }\{F\{F\{\operatorname{pupil}(x, y) \times \\ \left.\left.\left.\exp (i \varphi(x, y)) \times \operatorname{rec}\left(\frac{x}{w_{\mathrm{s}}}\right) \times \operatorname{rec}\left(\frac{y}{L_{\mathrm{s}}}\right)\right\}\right\}\right\} \end{array}$(12)

式(12)中, 函数angle{}返回相位角。

滤波狭缝后的解包裹像差φ _s(x, y)可以由式(13)给出

φs(x, y)=unwrap{phases(x, y), pupil(x, y)}(13)

式(13)中, 函数unwrap{}表示二维相位解缠绕操作符。

最终的图像重建过程可以表示为

O(x, y)=I(x, y)⊗PSFs(x, y)+n(x, y)

=I(x, y)⊗F{A0exp(iφs(x1, y1))}2+n(x, y)(14)

图像重建使用LR²A算法进行, 第(n+1)次迭代的重建图像可以表示为

In+1=InO(x, y)In⊗PSFs(x, y)⊕PSFs(x, y)(15)

式(15)中, “ 􀱇” 是非线性重建运算符, 定义为

A⊕B=F-1{|FA|αexp[iarg(FA)]|FB|βexp[iarg(FB)]}(16)

式(16)中, FA是A的傅里叶变换。 α 和β 在-1到1之间进行调节, 以最小化噪声。 在第一步中, 设定I¹=O(x, y), 并对其进行归一化处理, 然后计算O(x, y)与(I¹􀱋PSF_s(x, y))之间的比值。 下一步, 使用NLR(非线性相关)方法将此“ 比值” 与PSF_s(x, y)进行非线性相关处理, 得到的结果称为“ 残差(Residue)” 。 该“ 残差” 将乘以前一次迭代的结果, 即第n次迭代后的重建图像为Iⁿ。 这一过程不断迭代, 直到获得最佳的重建结果。 由于NLR提供了更优的估计, 因此该算法可以快速收敛。 基于前期大量预实验发现, 当α ∈ [0.8, 1.0] 且β =1.0时, 算法在重构精度与收敛速度之间达到较优平衡。 最终选择α =0.9、 β =1.0 是该稳定区间内的代表性取值。 虽然本工作未系统研究参数敏感性, 但参数自适应选择将是后续工作的重点。

通过上述理论分析, 我们可以看到该方法如何通过准确重建滤波后的相位, 并利用LR²A 算法来恢复因狭缝过滤效应导置的图像失真, 从而提高成像光栅光谱仪的光谱和空间分辨率。 这种方法不仅能够适应复杂的应用条件, 还能够在不使用自适应光学波前校正的情况下实现高质量的图像复原。

为了验证所提出的基于LR²A算法的波前像差评估和狭缝图像重建方法的有效性, 进行了数值模拟和实验验证。

2.1 系统描述

光栅光谱仪的光学结构如图2所示。 实验采用波长为632.8 nm、 半高全宽(FWHM)为1 pm的偏振HeNe激光器作为光源。 线偏振准直激光输出通过一个非偏振分束器分为两束强度几乎相等的光束。 其中一束被导向到LC-SLM(电寻址液晶空间光调制器), 而另一束则入射至哈特曼-夏克波前传感器(HS WFS)。 这两个反射光束随后由分束器重新合成并通过成像镜Lens2聚焦后进入光栅光谱仪。

图2

Fig.2

	Figure Option ViewDownloadNew Window
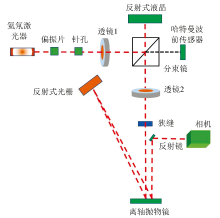	图2 本文所提出的光栅光谱仪, 其中LC-SLM用作像差生成器Fig.2 The proposed grating spectrometer, where LC-SLM used as aberration generator

在光栅光谱仪中, 光束经过狭窄的狭缝进行过滤。 狭缝宽度分别为50和100 μ m。 然后光束被离轴抛物面镜(OAP)准直并照射到光栅上。 光栅的槽密度为79条· mm^-1, 尺寸为220 mm× 110 mm× 30 mm, 购自Newport Richardson Grating公司。 最终, 光束由OAP汇聚并照射到相机上。 实验中使用了一个集成在相机前面的带通滤波器来实现不同衍射级次分离。

在本实验中, 使用了一个具有28× 28子孔径的哈特曼-夏克波前传感器(HS WFS)来测量光栅光谱仪的光学像差, 同时使用液晶空间光调制器(LC-SLM)作为像差生成器。 初始波前像差的均方根(RMS)值为0.15λ , 主要来源于LC-SLM。 为了更清晰地展示后续的狭缝图像重建过程, 我们使用LC-SLM进行波前校正, 将残余波前像差减少到约0.025λ , 从而接近衍射极限。

2.2 相位重构方法

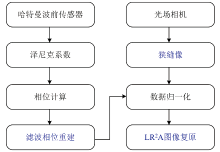
由于滤波狭缝的影响, 在进行狭缝图像复原之前需要重建相位。 相位重建的基本过程如下: (1) 由LC-SLM生成随机像差φ (x, y), 并通过具有28× 28子孔径的哈特曼-夏克波前传感器(HS WFS)检测; (2) 根据傅里叶理论, 近场E_nf-s可以通过式(11)计算。 (3) 通过式(12)和式(13)重建滤波相位。 采用angle{}函数计算相位角, 并返回复数数组的实部。 滤波后的波前相位被解包裹并准确重建。 (4) 将狭缝图像和重建的滤波相位归一化到0到1之间, 并使用LR²A算法恢复狭缝图像。 所提出方法的主要流程图如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 本文所提出方法的主要流程图Fig.3 The main flow chart of the proposed method

在实验中, 大气湍流相位屏符合Kolmogorov理论, 由3到36阶Zernike项组成, 去掉倾斜项。 通过LC-SLM随机生成像差φ ₁和φ ₂, 分别对应D/ro=7和10, 其中D是输入孔径直径, ro是Fried参数。 图像采样设置为512× 512。

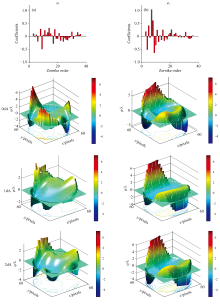
重建了不同狭缝宽度下的波前像差, 三维图展示了随机波前和重建波前像差, 如图4所示。 “ dA” 表示艾里斑直径, 实验中使用的狭缝宽度分别为1 dA和2 dA。 从图4可以看出, 经过狭缝滤波后, 波前像差的PV值和RMS值变小, 且明显可以看出, 波前像差的数值分量被滤除。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 在不同狭缝宽度下的滤波狭缝后的未重构波前像差和重构波前像差Fig.4 Unreconstructed wavefront aberration and reconstructed wavefront aberration after filter slit with different slit widths

2.3 重建图像分析

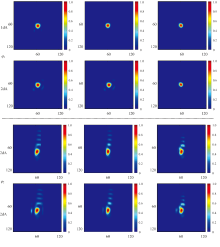
经过滤波相位的精确重建后, 进行了狭缝图像复原。 由于噪声是实验中的不可避免因素, 特别是Poisson噪声, 我们在数值狭缝图像中使用Matlab的imnoise函数随机添加了Poisson噪声。 进行了数值和实验验证, 结果如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同狭缝宽度的滤波狭缝对图像的影响 在每个子图中, 一对红色色虚线表示光谱仪狭缝; 图中的横坐标和纵坐标单位为像素Fig.5 The influence of filter slit with different slit widths on the image In each subplot, a pair of red dashed lines represents the slit; The horizontal and vertical coordinates in the figures are in pixels

从图5可以看出, 在φ ₁像差条件下, 由于整体像差较小, 无论是在1 dA还是2 dA狭缝宽度下, 狭缝滤波作用对图像的影响均较为微弱, 未重建图像、 重建图像与实验采集图像之间的差异也相对较小。 这说明在小像差条件下, 图像质量受滤波作用影响有限, 复原效果较好。

相比之下, 在φ ₂像差条件下, 由于像差较大, 无论是1 dA 还是2 dA狭缝条件, 狭缝滤波的作用显著增强。 此时, 未重建图像与重建图像之间在局部区域(如靠近狭缝边缘的光斑位置)表现出明显的亮度变化和结构差异。 尽管如此, 重建图像与实际采集的实验图像之间仍保持较好的一致性。

综上所述, φ ₁条件下图像复原结果与实验数据差异较小, 具备较高的一致性; 而φ ₂条件下则因像差和滤波作用增强, 造成图像细节丢失明显。 因此, 只有通过精确地进行滤波相位重建, 才能实现对狭缝图像的有效复原, 从而提高成像质量与系统分辨率。

2.4 小像差情况的狭缝图像复原

在相位重建之后, 使用LR²A算法对狭缝图像进行了重建, 并进行了数值和实验验证。 为了更好地评估图像复原质量, 采用SSIM(结构相似性指数)、 MSE(均方误差)、 ISNR(改进的信噪比)和PSNR(峰值信噪比)等评价指标对图像复原质量进行评价。 迭代次数设置为50次。 狭缝宽度分别为1和2 dA。 对φ ₁情况下的狭缝图像进行了复原。 如图4所示, 1 dA狭缝宽度包含了大部分狭缝图像细节。 然而, 当狭缝宽度从1 dA增加到2 dA时, 狭缝图像包含更多的噪声, 降低了图像信噪比。 在φ ₁情况下的图像复原结果如图5所示。

数值计算结果如图6所示, 经过50次迭代后: SSIM值约为1.0; MSE值约为1.5× 10^-5; 在1和2 dA情况下, ISNR值分别为7.365和6.947 dB; PSNR值在这两种情况下均约为96.8 dB。 在1和2 dA情况下的初始ISNR值分别为4.259和4.316 dB, 这表明实验中的噪声较小且更稳定, 因此随着狭缝宽度的变化, 噪声水平没有显著变化。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 在φ 1条件下使用LR2A算法的图像复原结果 在每个子图中, 一对红色虚线表示狭缝图像Fig.6 The image restoration results using LR2A in φ 1 case In each subplot, a pair of red dashed lines represents the slit

在实验重建过程中, 经过50次迭代后: SSIM值约为1.0; MSE值约为1.3× 10^-5; 在1和2 dA情况下, ISNR 值分别为8.308和8.482 dB; PSNR值在这两种情况下均约为96.8 dB。 结果表明, 当像差较小时, 狭缝宽度对图像复原的影响很小, 并且大部分细节和结构得以保留。 此外, 噪声水平对图像复原质量有显著影响, 即图像的信噪比对图像复原效果至关重要。 数值模拟和实验结果之间表现出良好的一致性。

2.5 大像差情况的狭缝图像复原

不同于φ ₁情况, 在φ ₂情况下, 除了噪声的影响外, 还存在更大的像差, 导致更多的图像细节会被窄狭缝过滤掉, 如图7所示。 显然, 较大的狭缝宽度会保留更多图像细节, 有利于图像重建。 然而, 较大的狭缝可能会引入更多噪声, 具体取决于实验条件的稳定性。

图7

Fig.7

	Figure Option ViewDownloadNew Window
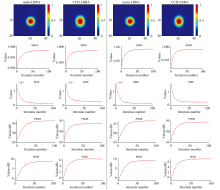	图7 在φ 2条件下使用LR2A算法的图像复原结果 在每个子图中, 一对红色虚线表示狭缝图像Fig.7 The image restoration results using LR2A in φ 2 case In each subplot, a pair of red dashed lines represents the slit

在存在较大像差及狭缝滤波限制的条件下, 图像的部分细节信息会丢失, 信噪比有所下降, 因此需要增加迭代次数以实现对狭缝图像的更精确复原。 综合考虑收敛速度与复原质量, 将迭代次数设定为100次。

在数值模拟中, 经过100次迭代后, SSIM值均接近于1.0, 表明重建图像与原始图像之间具有高度的结构相似性; MSE值约为1.3× 10^-5, 说明像素级误差极小; 在1和2 dA条件下, ISNR值分别为9.638和9.687 dB, PSNR值在两种情况下均达到约96.8 dB。 结果表明, 所提出的算法在数值仿真中实现了高质量的图像重建, 成像性能已接近衍射极限。

在实验重建方面, 同样进行100次迭代后, SSIM值仍保持在接近1.0的水平, MSE值约为2.5× 10^-5, 显示出较好的复原精度; 在1和2 dA条件下, ISNR值分别为6.096和6.656 dB, PSNR值分别约为93.5和94.1 dB。 虽然实验条件下的成像性能尚未完全达到衍射极限, 但整体图像复原效果仍较为理想, 具备较高的实用价值。

2.6 白光激光下的狭缝图像复原

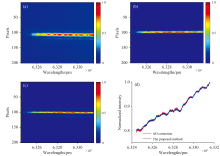
为验证太阳光栅光谱仪在白光条件下的成像性能, 实验中采用了Fianium公司生产的SC400白光激光器作为光源, 其输出光谱范围覆盖400~2 400 nm。 为获取自由光谱范围, 在相机前端加装了一个窄带通滤波片, 其中心波长为632 nm, 半高全宽(FWHM)约为1 nm。 基于本文所提出的方法, 开展了白光光谱图像的复原实验, 相关结果如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 白光光谱图像复原结果 (a): 探测图像; (b): AO校正结果; (c): 本方法; (d): (b)和(c)校正结果对比Fig.8 The white light image restoration results (a): Captured image; (b): AO correction; (c): The proposed method; (d): Comparative result of (b) and (c)

复原所得的狭缝光谱图像与自适应光学系统校正后的结果具有较高的一致性, 表明所提方法在白光光谱图像复原方面具有良好的有效性与实用性。 需要指出的是, 由于实验条件下无法获得白光光谱的真实参考图像, 因此该实验结果主要用于验证方法本身的可行性与复原能力。 然而, 与AO校正方法相比, 本方法依然能够实现对白光光谱信息的准确复原, 进一步说明其在实际应用中的稳定性和可靠性。

提出了一种新颖的方法, 用于波前像差评估与狭缝图像的联合复原, 而无需采用正则化技术。 该方法基于LR²A成像算法, 并结合Hartmann-Shack波前传感器对光栅光谱仪系统中的波前像差进行精确测量。 通过分析不同狭缝宽度条件下的滤波相位及系统的点扩散函数, 提升光谱成像质量。

据我们所知, 本文所提出的方法是目前少数可用于解决狭缝图像重建问题的有效手段之一。 其优势在于不仅适用于存在显著波前像差和低信噪比等复杂应用环境, 而且无需依赖自适应光学(AO)进行波前校正, 即可实现对狭缝图像的高质量复原。 此外, 实验结果表明, 该方法在宽谱段乃至白光条件下仍具有良好的适用性和稳定性, 为高光谱分辨率光栅光谱仪技术的发展提供了新的思路和技术支持。