引用本文
王绎嘉, 杨超博, 曹振, 彭江波, 俞南嘉, 韩明宏, 李蔚然, 张续腾, 于欣. 基于CH*发射光谱的火焰二维温度分布测量 [J]. 光谱学与光谱分析, 2025,45(11): 3098-3104.
WANG Yi-jia, YANG Chao-bo, CAO Zhen, PENG Jiang-bo, YU Nan-jia, HAN Ming-hong, LI Wei-ran, ZHANG Xu-teng, YU Xin. Measurement of Flame 2D Temperature Distribution Based on CH* Emission Spectra [J]. Spectroscopy and Spectral Analysis, 2025,45(11): 3098-3104.
Doi:10.3964/j.issn.1000-0593(2025)11-3098-07  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于CH*发射光谱的火焰二维温度分布测量
王绎嘉1,2, 杨超博1,2,*, 曹振1,2, 彭江波1,2, 俞南嘉3, 韩明宏1,2, 李蔚然3, 张续腾1,2, 于欣1,2
1.哈尔滨工业大学光电子技术研究所, 黑龙江 哈尔滨 150001
2.激光空间信息全国重点实验室, 黑龙江 哈尔滨 150001
3.北京航空航天大学宇航学院, 北京 100191
*通讯作者 e-mail: yangchaobo@hit.edu.cn

作者简介: 王绎嘉, 2001年生,哈尔滨工业大学航天学院及光电子技术研究所,激光空间信息全国重点实验室硕士研究生e-mail: Wangyj123000@163.com

收稿日期: 2025-07-10 修回日期: 2025-09-14 接受日期: 2025-09-14
基金: 国家自然科学基金项目(62305087)资助
摘要

温度是燃烧诊断领域中的关键参数之一, 获取火焰温度具有重要的科学意义和实用价值。 分子发射光谱测温技术因其具备非接触测量, 高测温上限, 测量系统简便等优势, 使得其常被用于高温高压等恶劣环境下的火焰温度测量。 由于光栅光谱仪狭缝的维度限制, 近年来关于该技术的研究多数仅限于零维和一维测量, 难以达成通过单次测量获得火焰二维温度场的目标。 因此在传统发射光谱测温系统的基础上加入一种二维转一维模块, 对发射光谱二维测温技术展开研究。 首先, 根据分子发射光谱测温原理建立发射光谱拟合测温算法, 形成发射光谱测温流程, 并将2 500 K转动温度下的CH*发射光谱仿真结果与分子发射光谱模拟软件LIFBASE生成的结果进行比对, 得到二者间的决定系数 R2=0.96, 验证了光谱拟合测温算法的可行性; 其次, 对二维转一维模块进行设计, 建立二维分布还原算法, 形成火焰二维温度分布信息的获取过程, 并基于二维转一维模块搭建发射光谱二维测量系统; 最后, 利用发射光谱二维测量系统对模型火箭发动机中局部火焰的CH*发射光谱进行二维测量, 对累加后的CH*发射光谱进行去噪去基线处理, 将仿真光谱与实测光谱进行拟合得出不同空间位置的温度, 再利用二维分布还原算法得到局部火焰二维温度分布情况和对应光谱拟合决定系数 R2分布。 从局部火焰二维温度分布测量结果中可得出本论文建立的测温系统能够对空间间隔为0.50 mm的两个温度数据点进行分辨, 且二维温度分布测量结果符合火焰形态; 在光谱拟合 R2二维分布中所有 R2>0.8, 且 R2>0.9的位置占比达76.5%, 验证了温度测量结果的可靠性。

关键词: 发射光谱; 二维测温; 光谱拟合
中图分类号:O433.4 文献标志码:A
Measurement of Flame 2D Temperature Distribution Based on CH* Emission Spectra
WANG Yi-jia1,2, YANG Chao-bo1,2,*, CAO Zhen1,2, PENG Jiang-bo1,2, YU Nan-jia3, HAN Ming-hong1,2, LI Wei-ran3, ZHANG Xu-teng1,2, YU Xin1,2
1. Institute of Opt-electronics, Harbin Institute of Technology, Harbin 150001, China
2. National Key Laboratory of Laser Spatial Information, Harbin 150001, China
3. School of Astronautics, Beihang University, Beijing 100191, China
*Corresponding author
Abstract

Temperature is one of the critical parameters in combustion diagnostics, and obtaining flame temperature holds important scientific significance and practical value. Molecular emission spectra thermometry, owing to its non-contact measurement capability, high upper temperature measurement limit, and simple system configuration, is frequently employed for flame temperature measurement in harsh environments characterized by high temperature and pressure. Constrained by the dimensional limitation of the slit in the grating spectrometer, most of the recent research on this technique has been confined to zero-dimensional (0D) and one-dimensional (1D) measurements, making it difficult to achieve the goal of obtaining a two-dimensional (2D) temperature field of flame through a single measurement. Therefore, this paper incorporated a 2D-to-1D conversion module into the traditional emission spectra temperature measurement system and investigated 2D emission spectra thermometry. Firstly, the emission spectral fitting thermometry algorithm was established based on the principle of molecular emission spectra thermometry, and the process of emission spectra thermometry was formulated. The simulated result of the CH* emission spectrum at a rotational temperature of 2 500 K was compared with the spectrum generated by the molecular emission spectrum simulation software LIFBASE, yielding the coefficient of determination ( R2) of 0.96. This verified the feasibility of the emission spectral fitting thermometry algorithm. Secondly, the 2D-to-1D conversion module was designed, a 2D distribution reconstruction algorithm was established, and the process for acquiring the 2D temperature distribution of the flame was developed. Furthermore, a 2D emission spectra measurement system was constructed based on the 2D-to-1D conversion module. Finally, the 2D emission spectra measurement system was employed to conduct 2D measurement of CH* emission spectra from the local flame within a model rocket engine. The accumulated CH*emission spectra were subjected to denoising and baseline removal. The temperatures at different spatial positions were derived by fitting simulated spectra to the measured spectra. Subsequently, the 2D distribution reconstruction algorithm was applied to obtain the local flame's 2D temperature field and the corresponding R2 profile of spectral fitting. From the measurement result of the 2D temperature distribution of local flame, it can be concluded that the temperature measurement system constructed in this paper is capable of resolving two temperature data points with the spatial interval of 0.50 mm, and the measurement result of 2D temperature distribution is consistent with the flame morphology. In the 2D distribution of spectral fitting R2, all R2 values are greater than 0.8, and positions with R2>0.9 account for 76.5%, which validates the reliability of the temperature measurement result.

Keyword: Emission spectra; 2D temperature measurement; Spectral fitting
引言

在燃烧诊断领域, 温度是表征燃烧性能的核心参数之一, 对火焰燃烧场温度精准测量的需求推动着高精度温度测量技术的发展。 当前, 常见的燃烧场温度测量技术包括热电偶测温[1, 2]、 基于激光诱导荧光的测温技术[3, 4]、 基于相干反斯托克斯拉曼散射的测温技术[5, 6, 7]、 辐射测温技术[8, 9, 10]、 基于可调谐半导体激光吸收光谱的测温技术[11, 12, 13]和分子发射光谱测温技术等。 已有相关研究证实, 上述测温技术已被逐步应用于实际工程场景, 实现了对燃烧场温度的有效测量。 例如, 天津大学张鹏[14]、 刘海峰等[15]对光学发动机缸内火焰燃烧特性展开研究, 通过使用基于Hottel-Broughton灰度模型的双色法来计算火焰温度, 最终得到缸内火焰燃烧温度范围, 并证实了计算结果能够反映缸内的实际温度情况; 华北电力大学Zheng[16, 17, 18]、 Cai等[19, 20]针对城市固体废物焚烧炉、 超燃冲压发动机等工程场景, 基于多光谱成像技术, 采用普朗克定律和Hottel、 多项式等发射率模型构建出辐射强度与温度的关系, 利用牛顿迭代法、 Levenberg-Marquardt等迭代算法计算出火焰二维温度分布情况, 并对温度测量结果的相对误差进行了评估。

在上述测温技术中, 分子发射光谱测温技术因为具有非接触式测量、 测量方式直接简便、 高测温上限的特点, 且同时具备适用于光学窗口受限、 高温高压等恶劣环境的优势, 已经成为了测温领域中比较热门的技术之一。 在近十几年来, 清华大学[21]、 四川大学[22]、 俄罗斯圣光机大学[23]、 美国普渡大学[24]、 中国科学院力学研究所[25]、 加拿大麦吉尔大学[26]、 哈尔滨工业大学[27]等研究机构对分子发射光谱测温技术做了较为详细的研究, 相关工作涵盖了对CH* 、 C2* 、 AlO等基团的辐射特性分析, 并成功将其应用于非接触式温度测量中。 然而, 在测量维度方面, 由于光栅光谱仪狭缝结构的限制, 当前基于分子发射光谱的温度测量研究大多仅实现了零维或一维温度获取, 即每次测量仅能获得燃烧场中某一空间点或一条线段上的温度分布, 针对火焰二维温度分布的测量研究相对较少, 面临一定的技术挑战。

为实现对火焰二维温度场的测量, 在传统发射光谱测量系统的基础上引入了一种二维转一维光学信息重组模块。 该模块可对火焰中指定区域的二维发射光谱信息进行重组转换, 将其映射为一维形式, 从而实现将二维平面内的光谱信息有效耦合进光栅光谱仪狭缝内, 突破其空间维度限制。

在测温分子选择方面, 选用火焰中的CH* 自由基, 原因主要在2个方面: 火焰中CH* 自由基的发射光谱在420~440 nm范围内特征峰较多, 不同温度下光谱特征峰之间相对强度差异较为明显; 不同于OH* 自由基, CH* 自由基理论上几乎不受自吸收效应影响[28], 测温结果相对会更加准确。

本论文的研究内容主要如下: 首先对分子发射光谱测温原理进行研究, 形成CH* 发射光谱仿真计算程序和发射光谱拟合测温算法; 之后对二维转一维模块进行设计, 并基于该模块搭建发射光谱二维测量系统, 对特定工况下模型火箭发动机中的局部火焰进行CH* 发射光谱二维测量; 最后利用发射光谱拟合测温算法与二维分布还原算法得出局部火焰的二维温度分布情况, 并通过分析火焰的二维温度分布特性, 结合各测量位置的光谱拟合决定系数R2对温度测量结果进行评估, 从而验证所获得的二维温度分布测量结果的合理性。

1 分子发射光谱测温技术研究
1.1 分子发射光谱测温原理

根据分子光谱学有关理论, 当上下能级的电子态, 振动态都固定时, 双原子分子的转动温度与发射光谱强度的关系如式(1)所示

I=CΦσ4exp-F(J')TrotSJ'J″(1)

式(1)中, Trot为分子转动温度, J'为上能级转动量子数, J″为下能级转动量子数, F(J')为上能级转动能量, SJ'J″为Honl-London因子, σ 为从上能级到下能级跃迁产生的光的波数, Φ 为由核自旋引入的倍率因子, C为常数, I为对应发射光谱强度。

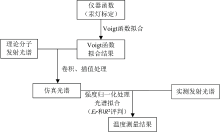
根据式(1)以及CH* 自由基的相关参数, 选取一系列J'分别进行发射光谱强度计算, 最终就能形成指定转动温度下的理论CH* 发射光谱。 但在实际测量时, 由于光谱测量系统会对发射光谱形成展宽效应, 原理上经过实验仪器采集到的光谱是理论发射光谱与实验仪器对应的仪器函数二者的卷积结果, 而仪器函数通常采用Voigt函数进行拟合。 因此, 可利用汞灯等标准光源, 选取特征谱线, 测量其经实验系统后的展宽光谱, 通过Voigt函数拟合该光谱, 得到实验系统的仪器函数。 在发射光谱测量实验中, 将理论发射光谱与仪器函数进行卷积处理, 即可生成与实验测量条件相一致的仿真光谱。

在温度获取环节, 本论文首先通过插值使仿真光谱的波长采样点与实测光谱的波长点位完全匹配, 之后对仿真光谱和实测光谱均进行强度归一化处理, 再基于最小二乘拟合方法形成发射光谱拟合测温算法, 以转动温度为优化参量, 以实测光谱为基准, 对仿真光谱进行形状上的逼近优化, 直到二者差别最小为止, 此时对应的转动温度即为温度测量结果。

通过计算不同波长点位的残差Er和两光谱的决定系数R2来表征仿真光谱与实测光谱的近似程度[29], 从而对光谱拟合效果进行评判。 二者的计算公式分别如式(2)和式(3)所示

Er(i)=Imea(i)-Isim(i)(2)

R2=1-∑i=1N[Isim(i)-Imea(i)]2∑i=1N[Imea(i)-I-mea]2(3)

式(2)和式(3)中, Imea表示某一波长点位上的实测光谱强度, Isim表示某一波长点位上的仿真光谱强度, I-mea表示全部波长点位上的实测光谱强度的平均值, i表示波长点位编号, N表示波长点位的总数量。

根据式(2)和式(3), 可看出当残差Er越接近于0, 决定系数R2越接近于1时, 说明对应转动温度下仿真光谱和实测光谱越接近, 即光谱拟合效果越好。

综上所述, 发射光谱测温流程如图1所示。 本论文构建的发射光谱拟合测温算法, 在实际操作中仅通过输入实测光谱与仪器函数即可直接输出对应温度信息, 操作流程简洁高效。 该算法不仅实现了测温过程的便捷化, 更有效弥补了现有分子发射光谱模拟软件(如LIFBASE等)仅能通过输入温度生成光谱, 却无法由输入光谱反演对应温度的技术局限。

图1 发射光谱测温流程图Fig.1 Flowchart of emission spectra thermometry

1.2 CH* 发射光谱的仿真

由于LIFBASE等分子发射光谱模拟软件仅能通过输入特定转动温度生成对应光谱, 无法参与到以转动温度为优化参量的光谱拟合过程中, 故需要建立一种以转动温度为变量的发射光谱仿真计算模型。 该模型与光谱拟合测温算法相适配, 通过将不同转动温度下的仿真光谱与实测光谱进行比对, 确定两光谱形状最为接近时对应的转动温度值, 从而实现火焰温度测量。

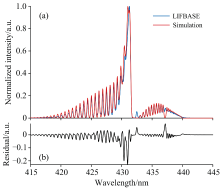
基于分子发射光谱测温原理, 结合CH* 分子的相关参数, 建立了CH* 发射光谱仿真计算程序。 仿真程序中, 上能级转动量子数J'取值范围为0~80, 转动温度设定为2 500 K。 设定合适的Voigt函数作为仪器函数(使用Voigt函数的半高全宽FWHM=0.24 nm), 用来模拟仪器响应特性。 随后, 利用分子发射光谱模拟软件LIFBASE生成对应温度与仪器函数下的CH* 发射光谱, 并将仿真得到的CH* 发射光谱与其进行了比较, 如图2(a)所示。 图2(a)中蓝色曲线代表从LIFBASE软件中得到的CH* 发射光谱, 橙色曲线代表仿真得到的CH* 发射光谱。 以LIFBASE软件生成的CH* 发射光谱作为实测光谱进行分析, 得到二者的残差分布如图2(b)所示, 从残差分布上也能看出除光谱强度最高点附近某些位置残差绝对值超过0.2外, 其余绝大多数位置的残差绝对值均小于0.1, 这证明了两光谱在走势上大体重合。 利用决定系数R2对两光谱的近似程度进行评判, 得到R2的计算结果为0.96, 说明两光谱形状十分接近, 验证了仿真程序的实用性和光谱拟合测温算法的可行性。

图2 (a)CH* 发射光谱仿真结果; (b)残差分布Fig.2 (a) CH* emission spectrum simulation result; (b) Residual distribution

2 实验部分
2.1 二维转一维模块

本研究完成了对二维转一维模块的设计工作, 该模块的构造和原理如下:

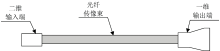
二维转一维模块的结构如图3所示, 其由二维输入端、 光纤传像束、 一维输出端三部分构成。 该模块实现降维的核心部件为1 024个光纤, 这些光纤在二维输入端排布成32× 32 的二维光纤阵列, 经过位置重组后在一维输出端转变为1 024× 1的一维光纤阵列排布, 从而实现光学信息由二维到一维的维度转换。 实验过程中一维输出端的光纤阵列长度为32 mm。

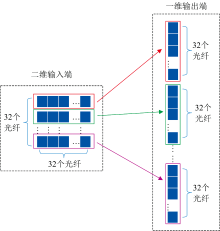
图3 二维转一维模块结构图Fig.3 Schematic of the 2D-to-1D conversion module

二维转一维模块的光纤重组排布过程如图4所示。 从图4 可以看出, 在一维输出端的光纤阵列中, 其空间排布与二维输入端的光纤阵列存在明确的对应关系: 一维输出端顶部的32个光纤, 对应二维输入端沿垂直方向(从上至下)排列的第一行光纤; 自该组光纤向下延续的32个光纤, 则对应二维输入端垂直方向上的第二行光纤; 此类对应关系依序递推。

图4 二维转一维模块的光纤重组排布示意图Fig.4 Schematic of the fiber reorganization in the 2D-to-1D conversion module

为了得到最终的二维温度分布情况, 在得到温度数据后需要一种二维分布还原算法, 将温度从一维分布按顺序还原为二维分布。 采用的二维分布还原算法, 其实现效果等价于二维转一维模块中光纤重组排布的逆过程。

基于该二维转一维模块和二维分布还原算法, 可实现火焰二维温度分布信息的获取, 具体过程如下: 首先获取二维视场范围内局部火焰的CH* 发射光谱, 并通过二维转一维模块将火焰发射光谱信息从二维分布重组为一维分布; 之后利用发射光谱拟合测温算法得到对应温度的一维分布情况; 最后利用二维分布还原算法重构出局部火焰二维温度分布情况。

2.2 实验装置与光谱测量方案

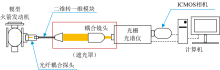
为了实现发射光谱二维测温, 搭建了含有二维转一维模块的发射光谱二维测量系统, 并与北京航空航天大学宇航学院合作, 完成了对特定工况下小尺度模型火箭发动机内部局部火焰二维温度分布的测量(该工况下的理论燃烧温度为3 176 K), 实验装置如图5所示。 模型火箭发动机带有小光学窗口, 并且在该窗口处设计了固定光纤耦合探头的卡口。 发射光谱二维测量系统由光纤耦合探头、 二维转一维模块、 耦合镜头、 光栅光谱仪、 ICMOS相机构成。 使用光纤耦合探头是为了实现小光学窗口条件下的光学信息传输, 它的末端设有固定二维输入端的卡口, 从而将火箭发动机中火焰的自发辐射光耦合到二维转一维模块的二维光纤阵列中。 在二维转一维模块的一维输出端与光栅光谱仪的狭缝之间设置耦合镜头, 该镜头用来将从二维转一维模块的一维输出端处出射的一维线光完整地耦合到光栅光谱仪的狭缝中。 为避免环境背景光对发射光谱测量产生干扰, 实验中使用不透光罩体对一维输出端至光谱仪狭缝的光路区段进行密封处理, 确保实验装置与外界环境光实现物理隔离。

图5 CH* 发射光谱测量装置示意图Fig.5 Schematic of CH* emission spectra measurement experimental setup

在实验中, 首先使用汞灯光源435.84 nm的特征谱线来对系统仪器函数进行测量, 并用Voigt函数分别拟合不同空间位置的汞灯光谱得到对应空间位置上系统仪器函数信息。 之后进行点火, 测量局部火焰的CH* 发射光谱, 测量过程如下: 模型火箭发动机中局部火焰的CH* 发射光谱通过发动机的光学窗口到达光纤耦合探头处, 经过探头耦合到二维转一维模块的二维输入端处, 并在该模块中做降维重组, 从原来的二维信号转换为一维信号。 从一维输出端出射的一维线光通过耦合镜头压缩进入光谱仪狭缝中, 经过光谱仪分光最终在ICMOS相机上探测到CH* 发射光谱。

为了获取足够的光谱分辨率, 实验中光栅光谱仪内部选用刻线数为1 800 l· mm-1的光栅; 光谱仪中心波长设为430 nm, 与CH* 发射光谱的波段对应; 光谱仪狭缝宽度设为500 μ m。 为保证获得信噪比高的发射光谱信号, ICMOS相机的探测门宽设为500 ms, 增益设为3 000。 实验中连续拍摄15张CH* 发射光谱一维分布图像。

3 结果与讨论
3.1 光谱处理与拟合效果

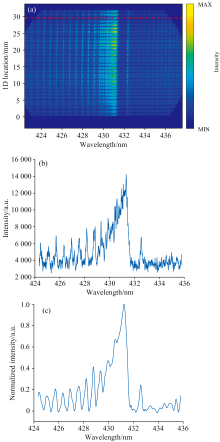
在得到模型火箭发动机中局部火焰的CH* 发射光谱后, 首先对采集到的15张图像中含有效信号的部分图像进行强度累加处理, 形成1张累加后的发射光谱一维分布图像, 如图6(a)所示, 以减小测量时随机噪声产生的影响。 图6(a)中横坐标对应CH* 发射光谱的波长信息, 纵坐标对应一维光纤阵列的空间位置信息。

图6 (a) CH* 发射光谱一维分布图像; (b) 处理前的CH* 发射光谱; (c) 去噪去基线后的CH* 发射光谱Fig.6 (a) 1D distribution image of CH* emission spectra; (b) CH* emission spectrum before processing; (c) CH* emission spectrum after denoising and baseline removal

为消除噪声与基线对光谱拟合的干扰, 需要对图6(a)中不同空间位置的CH* 发射光谱进行去噪和去基线处理。 在本论文中使用小波滤波法对实测CH* 发射光谱进行去噪, 之后对于428.5~432.0 nm波段范围之外的光谱数据, 选取部分局部最低点, 并利用4次多项式拟合形成实测光谱全部波段范围内的基线信息, 将去噪后的光谱与拟合基线进行强度相减获得相应光谱数据, 最后对光谱数据进行强度归一化处理得到最终实测光谱。 图6(b)与图6(c)分别呈现了对图6(a) 中红色虚线所示位置处实测CH* 发射光谱进行处理前与处理后的效果。

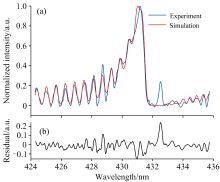
在对实测光谱进行处理后, 利用发射光谱拟合测温算法, 以转动温度为优化参数, 上能级转动量子数J'取值范围为0~45, 将对应仪器函数下的仿真光谱与相同空间位置的实测光谱进行拟合, 得到二者差异最小时对应的转动温度值。 对图6(c)中CH* 发射光谱进行拟合的效果如图7(a)所示, 其中蓝色曲线代表实测光谱, 橙色曲线代表仿真光谱, 通过光谱拟合得到该位置的温度计算结果为2 851 K。 实测光谱与仿真光谱的拟合残差分布如图7(b)所示, 从图7(b)中可看出两光谱绝大多数位置的残差绝对值均小于0.2, 证明了两光谱的形状和趋势相近。 利用决定系数R2来评判图7(a) 的光谱拟合效果, 计算得到R2数值为0.95, 说明两光谱拟合效果良好。 若不对实测光谱进行小波滤波去噪处理, 直接进行去基线与强度归一化处理后进行光谱拟合, 得到的拟合R2数值为0.81, 低于滤波后的计算结果, 这说明未进行去噪情况下光谱拟合效果较差, 进而会影响温度测量的准确度。 在图7(a)中, 实测光谱在432.5 nm附近存在明显的光谱峰, 而在仿真光谱中却不存在该光谱峰, 推测该光谱峰可能为Hγ 线[30]。

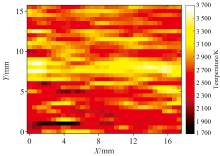
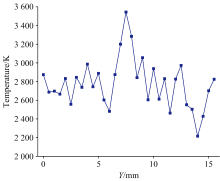
图7 (a)光谱拟合效果; (b)残差分布Fig.7 (a) Spectral fitting result; (b) Residual distribution

3.2 二维温度分布测量结果

在得到CH* 发射光谱一维分布图像后, 利用发射光谱拟合测温算法计算图像中不同位置光谱对应的温度信息, 共得到1 024个温度数据, 按照对应一维空间位置排布形成温度的一维分布结果, 之后利用二维分布还原算法重构得到32× 32 的局部火焰二维温度分布结果, 如图8所示, 与二维转一维模块的二维光纤阵列排布相对应。 图8中的横纵坐标表示局部火焰的空间位置信息, 在X方向上相邻温度数据点的间隔为0.56 mm, 在Y方向上相邻温度数据点的间隔为0.50 mm, 整体分辨率处于较高水平。 图8中X方向的探测长度与Y方向的探测长度存在差异, 其原因在于: 二维转一维模块中, 二维光纤阵列沿Y方向的排列密度更高, 导致最终二维视场在Y方向的探测范围短于X方向。

图8 二维温度分布测量结果Fig.8 2D temperature measurement result

从图8可以看出, Y方向上局部火焰二维温度分布整体呈现中间高两边低的趋势, 该分布特点与实际火焰形态相符。 为了直观体现该特点, 对二维温度分布测量结果进行沿Y方向的温度提取, 这里选择图8中X=14 mm位置对应的32个温度数据, 得到的一维温度分布情况如图9所示。 从图9 可以看出, 在测量范围中间区域Y=7~8 mm对应的3个温度数据均不低于3 200 K, 明显高于其他位置的温度(其他位置的温度均小于3 100 K), 进一步说明了局部火焰温度在Y方向上分布具有中间高两边低的特点。

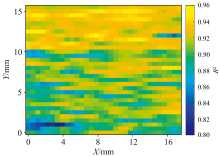
图9 提取后的一维温度分布结果Fig.9 1D temperature profile result after extraction

与图8的二维温度分布测量结果相对应, 光谱拟合R2的二维空间分布结果如图10所示。 从图10可看出, R2的整体数值分布在0.81~0.95范围内, 均在0.8以上, 且在1 024个不同位置中, 有783处的R2高于0.9, 占比达76.5%, 表明整体的发射光谱拟合效果良好。

图10 光谱拟合R2的二维分布Fig.10 2D profile of R2 in spectral fitting

对图10进行分析, 可看出上侧R2数值明显比下侧R2数值高, 这可能是因为在对发射光谱测量系统进行对焦时, 一维输出端上半部分的对焦效果优于下半部分, 从而使得上半部分对应发射光谱的信噪比更优。 同时, 在局部区域存在R2偏低的情况(例如图10左下方部分区域), 这些区域在如图8所示的温度测量结果中往往体现为温度过低或温度过高, 这可能是由于二维转一维模块中的部分光纤损耗过大甚至可能出现损坏, 使得对应区域得到的发射光谱信噪比较差, 从而导致拟合效果相对较差, 最终出现温度测量结果偏离实际值的情况。

4 结论

本论文完成了基于CH* 发射光谱的火焰二维温度分布测量。 在测温方法上, 对分子发射光谱测温技术进行了研究, 形成了CH* 发射光谱拟合测温算法和测温流程, 并进行了指定温度下CH* 发射光谱的仿真, 得到仿真结果与LIFBASE软件生成光谱之间的决定系数R2=0.96, 验证了测温算法的可行性。 此外, 设计了一种二维转一维模块和对应二维分布还原算法, 基于该模块搭建了发射光谱二维测量系统, 并对模型火箭发动机进行了局部火焰二维温度分布测量, 通过发射光谱拟合测温算法和二维分布还原算法得到了局部火焰二维温度分布测量结果和对应光谱拟合决定系数R2的二维分布。 通过对结果进行分析得出: 测温系统能够分辨空间间隔为0.50 mm的两个温度数据点, 二维温度分布测量结果与实际火焰形态相符, 对应光谱拟合R2均高于0.8, 且R2> 0.9的位置占全部区域的76.5%, 表明温度测量结果的合理性。 本论文实现了火焰温度的二维直观测量, 后续可在发射光谱测量装置、 光谱拟合测温算法等方面进行优化。

参考文献
[1] Aizawa T, Harada T, Kondo K, et al. International Journal of Engine Research, 2017, 18(5-6): 453. [本文引用:1]
[2] Elias J, Faccinetto A, Batut S, et al. International Journal of Thermal Sciences, 2023, 184: 107973. [本文引用:1]
[3] Foo K K, Lamoureux N, Cessou A, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2020, 255: 107257. [本文引用:1]
[4] Swain W, Wang Y, Parajuli P, et al. Experiments in Fluids, 2023, 64(4): 71. [本文引用:1]
[5] Stauffer H U, Rahman K A, Slipchenko M N, et al. Optics Letters, 2018, 43(20): 4911. [本文引用:1]
[6] Lowe A, Thomas L M, Satija A, et al. Proceedings of the Combustion Institute, 2019, 37(2): 1383. [本文引用:1]
[7] Barros J, Scherman M, Lin E, et al. Optics Express, 2020, 28(23): 34656. [本文引用:1]
[8] Wang Q, Li Z, Li C, et al. Applied Physics B, 2021, 127(3): 36. [本文引用:1]
[9] Zheng S, Cai W, Zhao C, et al. Measurement, 2022, 196: 111272. [本文引用:1]
[10] Zhu W, Li X, Peng J, et al. Applied Energy, 2022, 327: 120065. [本文引用:1]
[11] Wang G, Mei B, Liu X, et al. Proceedings of the Combustion Institute, 2019, 37(2): 1589. [本文引用:1]
[12] Wang Z, Deguchi Y, Kamimoto T, et al. Fuel, 2020, 268: 117370. [本文引用:1]
[13] Sentko M M, Schulz S, Stelzner B, et al. Combustion and Flame, 2020, 214: 336. [本文引用:1]
[14] ZHANG Peng, TANG Qing-long, CHEN Bei-ling, et al(张鹏, 唐青龙, 陈贝凌, 等). Transactions of CSICE(内燃机学报), 2014, 32(6): 489. [本文引用:1]
[15] LIU Hai-feng, WEN Ming-sheng, YANG Zhi, et al(刘海峰, 文铭升, 杨智, 等). Transactions of CSICE(内燃机学报), 2020, 38(3): 200. [本文引用:1]
[16] Zheng S, Cai W, Sui R, et al. Fuel, 2022, 323: 124328. [本文引用:1]
[17] Zheng S, Cai W, Liu B, et al. Fuel, 2023, 333: 126391. [本文引用:1]
[18] Zheng S, Jia Q, Cai W, et al. Physics of Fluids, 2025, 37(3): 035105. [本文引用:1]
[19] Cai W, Zheng S, Jia Q, et al. Physics of Fluids, 2025, 37(4): 045120. [本文引用:1]
[20] Cai W, Zheng S, Zhu J, et al. Physics of Fluids, 2025, 37(4): 045124. [本文引用:1]
[21] PENG Zhi-min, DING Yan-jun, YANG Qian-suo, et al(彭志敏, 丁艳军, 杨乾锁, 等). Acta Physica Sinica(物理学报), 2011, 60(5): 053302. [本文引用:1]
[22] Zhang C, Tang H, Zhang C, et al. Chemical Physics Letters, 2013, 556: 13. [本文引用:1]
[23] Mekhrengin M, Miroshnichenko G, Chistiakov A, et al. Measurement, 2020, 166: 108242. [本文引用:1]
[24] Ruesch M D, McDonald A J, Mathews G C, et al. Proceedings of the Combustion Institute, 2021, 38(3): 4365. [本文引用:1]
[25] Zhou G, Li F, Lin X, et al. Measurement Science and Technology, 2023, 34(5): 054001. [本文引用:1]
[26] Yu T, Mangalvedhe K, Francoeur M, et al. Combustion and Flame, 2024, 263: 113421. [本文引用:1]
[27] Zhang X, Yang C, Yuan X, et al. Chinese Physics B, 2025. (Accepted, doi: 10.1088/1674-1056/ade24a) [本文引用:1]
[28] ZHANG Zhong-lin, YANG An-long, WANG Jiang, et al(张仲磷, 杨岸龙, 王江, 等). Chinese Optics(中国光学), 2024, 17(5): 1014. [本文引用:1]
[29] Zhao C, Yu L, Liang J, et al. Optical Engineering, 2022, 61(1): 015104. [本文引用:1]
[30] Pastol A, Catherine Y. Journal of Physics D: Applied Physics, 1990, 23(7): 799. [本文引用:1]