基于相关系数热力图的水中重金属光谱可分性讨论及遥感反演波段选择策略

引用本文

梁业恒, 劳小敏, 邓孺孺, 倪桦泓, 赵彤彤, 黄岸峰, 郭志鹏, 李玉华, 张瑞午. 基于相关系数热力图的水中重金属光谱可分性讨论及遥感反演波段选择策略[J]. 光谱学与光谱分析, 2025,45(11): 3057-3065.
LIANG Ye-heng, LAO Xiao-min, DENG Ru-ru, NI Hua-hong, ZHAO Tong-tong, HUANG An-feng, GUO Zhi-peng, LI Yu-hua, ZHANG Rui-wu. Spectral Separability Analysis and Band Selection for Heavy Metal Inversion in Water Using Correlation Coefficient Heatmaps[J]. Spectroscopy and Spectral Analysis, 2025,45(11): 3057-3065.
Doi:10.3964/j.issn.1000-0593(2025)11-3057-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于相关系数热力图的水中重金属光谱可分性讨论及遥感反演波段选择策略

梁业恒¹, 劳小敏², 邓孺孺^1,^3,^*, 倪桦泓¹, 赵彤彤¹, 黄岸峰⁴, 郭志鹏⁵, 李玉华⁶, 张瑞午¹

1.中山大学地理科学与规划学院, 广东广州 510006

2.澳门城市大学城市与可持续发展研究院, 澳门 999078

3.南方海洋科学与工程广东省实验室(珠海), 广东省水环境遥感监测工程技术研究中心, 广东珠海 519082

4.佛山市自然资源局禅城分局, 广东佛山 528000

5.广州市城市规划勘测设计研究院有限公司, 广东广州 510030

6.天津市地质环境监测总站, 天津 300191

*通讯作者 e-mail: eesdrr@mail.sysu.edu.cn

作者简介: 梁业恒, 1987年生,中山大学地理科学与规划学院助理研究员 e-mail: liangyeheng@163.com;劳小敏, 1988年生,澳门城市大学城市与可持续发展研究院博士研究生 e-mail: laoxiaom@hzu.edu.cn

梁业恒,劳小敏:并列第一作者

收稿日期: 2025-04-30 修回日期: 2025-08-18 接受日期: 2025-08-18

基金: 南方海洋科学与工程广东省实验室(珠海)项目(311024015),国家自然科学基金项目(41901352),广东省基础与应用基础研究基金(2022B1515130001, 2020A1515010780),广州市科技计划项目(202102020454),广东省省级科技计划项目(2017B020216001)资助

摘要

城市经济高速发展的同时兼顾保护环境的“绿色经济”已是当今社会的共识。利用卫星、无人机遥感监测新手段, 再配合传统方式, 可形成立体化的监测体系, 使经济和环保间取得更高效的平衡。如何突破那些仍未能被遥感提取的参数的技术瓶颈, 是进一步扩大遥感应用的关键。水体重金属遥感作为环境遥感中一个有待解决又颇具应用价值的研究方向, 恰恰面临在卫星遥感反演中多参数求解的可分性难题。鉴于此, 首先利用光谱仪测量获得硫酸铜、铁氰化钾、亚铁氰化钾、氯化铁在波长范围350~1 050 nm的反射光谱, 结果发现: 硫酸铜在波长441 nm有一反射峰; 氯化铁呈“波浪式”缓慢增加至波长906 nm后开始缓慢减少; 铁氰化钾在波长767 nm出现反射峰; 亚铁氰化钾在波长826 nm出现反射峰, 而在波长988 nm有一反射谷。这四种化合物反射率光谱有两处相交位置: 硫酸铜和亚铁氰化钾在波长492 nm相交; 硫酸铜、氯化铁、铁氰化钾三者相交于576~584 nm(中心波长580 nm)波长范围。以此提出“比值铜指数Ratio Copper Index(RCI)”区分硫酸铜与这三种铁化合物。进一步地, 选用了两种遥感模型来剖析光谱可分性的数理意义, 并以混合像元信息线性分解模型为例, 计算十种重金属化合物(硫酸铜、铁氰化钾、亚铁氰化钾、氯化铁、氧化镉、四氧化三铅、铬酸铅、硫化镉、硫酸铅、硫化铅)的反射率在四种光谱分辨率下的彼此间相关系数, 然后生成对应热力图, 并讨论其可分性的变化情况, 结果发现这十种重金属化合物之间很多有关可分性现象有价值的规律和参考依据。最后给出一种依据相关系数热力图结果动态调整化合物数目和光谱分辨率的遥感反演波段选择策略。深入讨论了不同化合物之间的光谱可分性与遥感模型求解二者之间的数理本质, 进一步深化求解遥感模型的算法理论基础, 有望推动卫星影像层面的水体重金属遥感反演研究进展。

关键词: 环境遥感; 水体重金属遥感; 光谱可分性; 相关系数热力图

中图分类号:O433.4 文献标志码:A

Spectral Separability Analysis and Band Selection for Heavy Metal Inversion in Water Using Correlation Coefficient Heatmaps

LIANG Ye-heng¹, LAO Xiao-min², DENG Ru-ru^1,^3,^*, NI Hua-hong¹, ZHAO Tong-tong¹, HUANG An-feng⁴, GUO Zhi-peng⁵, LI Yu-hua⁶, ZHANG Rui-wu¹

1. School of Geography and Planning, Sun Yat-sen University, Guangzhou 510006, China

2. Institute of Urban and Sustainable Development, City University of Macau, Macau 999078, China

3. Southern Marine Science and Engineering Guangdong Laboratory(Zhuhai), Guangdong Engineering Research Center of Water Environment Remote Sensing Monitoring, Zhuhai 519082, China

4. Chancheng Branch of Foshan Natural Resources Bureau, Foshan 528000, China

5. Guangzhou Urban Planning and Design Survey Research Institute Limited Company, Guangzhou 510030, China

6. Tianjin Institute of Geological Environment Monitoring, Tianjin 300191, China

*Corresponding author

LIANG Ye-heng and LAO Xiao-min: joint first authors

Abstract

The concept of “green economy”, which balances rapid urban economic development with environmental protection, has become a societal consensus. Integrating emerging remote sensing technologies (e. g., satellites and drones) with traditional methods can establish a multidimensional monitoring system, enabling a more efficient balance between economic and environmental goals. A critical challenge for expanding remote sensing applications lies in overcoming technical bottlenecks related to parameters that cannot be extracted via remote sensing. Monitoring heavy metals in water, a valuable yet unresolved area of environmental remote sensing, encounters the issue of spectral separability in multi-parameter inversion through satellite remote sensing. To address this, the reflectance spectra of four compounds (copper sulfate, potassium ferricyanide, potassium ferrocyanide, and ferric chloride) were measured using a spectrometer within the wavelength range of 350~1 050 nm. Key findings include: Copper sulfate exhibits a reflectance peak at 441 nm; Ferric chloride shows a “wave-like” gradual increase until 906 nm, followed by a decline; Potassium ferricyanide peaks at 767 nm; Potassium ferrocyanide peaks at 826 nm, with the latter having a trough at 988 nm. The reflectance spectra of these four compounds intersect at two places: copper sulfate and potassium ferrocyanide intersect at a wavelength of 492 nm, while copper sulfate, ferric chloride, and potassium ferricyanide intersect in the wavelength range of 576~584 nm (centered at 580 nm). Consequently, the Ratio Copper Index (RCI) was proposed to differentiate copper sulfate from the three iron compounds. Two remote sensing models were employed to analyze the mathematical principles behind spectral separability. Utilizing a linear spectral unmixing model, pairwise correlation coefficients among ten heavy metal compounds (copper sulfate, potassium ferricyanide, potassium ferrocyanide, ferric chloride, cadmium oxide, lead tetroxide, lead chromate, cadmium sulfide, lead sulfate, and lead sulfide) were calculated across varying spectral resolutions and visualized through heatmaps. The results showed that there are many valuable phenomena, laws, and references about the separability between these ten heavy metal compounds. Ultimately, a dynamic band selection strategy for remote sensing inversion was proposed, which adjusts the number of compounds and bands in accordance with correlation heatmap results. The research results provide a deep discussion of the mathematical nature of spectral separability between compounds and the solution of remote sensing models, further deepening the algorithmic theoretical basis for solving remote sensing models. This research promotes the implementation of heavy metal concentration inversion in water at the satellite image level in the future.

Keyword: Remote sensing of environment; Remote sensing of heavy metals in water; Spectral separability; Correlation coefficient heatmap

文章图片

引言

在城市高速发展进程中, “ 绿色经济” 成为可持续发展核心议题。其中无人机、卫星等遥感技术凭着大范围、快速获取地表影像的优势, 被广泛用于各类资源与环境监测。随着载荷探测光谱分辨率不断提升, 遥感可反演参数越来越丰富, 如亚像元级别的城市土地利用/土地覆盖分类、城市变化^{[1, 2]}、植被覆盖度^{[3, 4]}, 水质遥感方面的悬浮泥沙、叶绿素a、有机污染物浓度等^{[5, 6, 7]}。

随着高光谱影像的出现, 以往一直备受质疑遥感反演可行性的水体重金属也有了提取潜力^[8]。在地表水质量标准中, 由重金属衍生相关的化合物种类可达十数种, 那么遥感反演时就面临一个重要问题, 各种化合物之间的光谱可分性如何? 针对这类问题, 学者通常是采用不同的指标, 如皮尔逊相关系数(下简称“ 相关系数” )、主成分分析、导数光谱等是较常用评价指标^[9], 提取不同物质的“ 光谱特征” , 然后通过经验回归方法建立特征波段(或波段组合)与实测值的遥感模型。由于提取特征的方法和指标多样, 学者开始结合机器学习、神经网络、分层建模等自动寻优方法^{[10, 11]}。但上述研究成果侧重于如何通过大量实测值来构建模型, 此类模型简单易行, 但终究会被这个实测值训练区所制约。而普适性更强的物理分析模型是定量遥感发展趋势, 其数学函数形式基本确定, 但随着求解参数增加, 会发现方程组解空间不稳定性也随之增加, 所以求解出这类数学模型的真解, 则需要剖析“ 光谱可分性” 的数理本质。类似研究仍鲜有报道。

上述问题可以理解为: 如何选择影像波段去构建一个合适方程组并求解出合理参数值, 如水体像元里各种重金属丰度或浓度。目前卫星数据的光谱分辨率有多种, 从由几个波段组成的多光谱到上百个波段的高光谱再到几百个波段的超光谱数据。可以说不同情形下, 联立得到的方程组千变万化, 例如, 从100个波段中筛选并组成方程组求出7个未知量, 此方程组就有160亿余种的组合, 而且这个组合数随着波段数目和求解变量个数的增加, 呈爆炸式增长。由于存在随机扰动和人为测量误差, 会发现不同组合得到的方程组解出的答案还不一定一样。尽管依赖现代计算机处理能力或许给予足够长时间演算能硬性穷举得到所谓的“ 最佳波段组合” , 但这对揭示里面各重金属特征响应波段是如何影响卫星影像反射率的物理机制未必是好事。

考虑到水体重金属污染源于自然和人为两方面因素, 其中以人为因素为主, 即采选矿、冶炼、印染等工业活动产生的含重金属废水未经处理排入河流、水库、湖泊, 导致污染。这些废水中含有多种重金属化合物, 例如: 硫酸铜是铜矿在氧化或酸浸过程中生成的化合物, 常见于冶金废水, 也是颜料原料; 氯化铁和铁氰化钾, 广泛用于建筑、染料和冶金工业^[12]; 镉和铅化合物(如硫化镉、铬酸铅), 主要通过电镀、电池制造废水进入自然水体^[13]。这些化合物在作者前期开展的光学参数测量实验结果中, 已发现其在可见光-近红外波段具有特征光谱响应^{[12, 13, 14]}, 从而会导致重金属污染水体的反射或吸收光谱与正常水体产生差异性。

所以, 这次实验选择在水环境较容易产生重金属污染事故的铜、铁、镉、铅元素有关的十种典型化合物, 即硫酸铜、铁氰化钾、亚铁氰化钾、氯化铁、氧化镉、四氧化三铅、铬酸铅、硫化镉、硫酸铅和硫化铅。通过测量它们的反射率光谱, 生成相关系数热力图, 分析在四种不同光谱分辨率下, 彼此间光谱可分性如何变化?最终通过线性代数理论, 提出一种有数理意义的光谱可分方法流程, 进而给出遥感反演波段选择策略。研究成果有助于突破未来落实到卫星影像层面上反演水体重金属时的技术瓶颈, 提供求解遥感模型的算法技术支撑, 推动其在高光谱遥感影像反演研究的深入发展。

1 方法与原理

1.1 水中重金属遥感模型的矩阵表达

假设离水反射率与重金属参数之间的函数关系可用式(1)表示

$R_{wo} (λ_{i}) = f (X_{j})$ (1)

式(1)中, λ _i代表光谱数据第i个波段的波长值, i=1, 2, …, m; m为参与反演的总波段数目; R_wo(λ _i)表示波长λ _i的离水反射率; X_j代表第j种重金属化合物的参数(如丰度、浓度等), 是未知量, j = 1, 2, …, n; n为重金属化合物总数目; 抽象函数f代表某个用于反演水中重金属参数的遥感模型。

对于每个波长λ _i都可以列出形如式(1)的方程, 然后联立m个式(1)组成方程组, 经过适当数学整理后, 则可用矩阵形式表示如式(2)

$AX = B$ (2)

式(2)中, A为该方程组m× n的系数矩阵; X为该方程组n× 1 个未知数组成的列向量; B为该方程组m× 1的常数项列向量。

具体地, 下面对式(1)抽象函数f选择常用的两类情形对式(2)作进一步展开, 以更好阐述实验原理。

情形一, 函数f数学表达式为“ 混合像元信息线性分解模型” , 具体建模原理参见文献[3, 4]。即对每个像元进行亚像元级别的不同重金属化合物丰度提取。模型数学表达式如式(3)

$R_{wo} (λ_{i}) = f (X_{j}) = \sum_{j = 1}^{n} a_{j} R_{j} (λ_{i})$ (3)

式(3)中, R_j(λ _i)表示波长λ _i的第j种重金属化合物的反射率; a_j即第j种重金属化合物的丰度。其中, 各种重金属化合物反射率光谱数据需要实验测量获得。选择干燥晴天, 利用光谱仪分别对标准板和样品进行辐亮度测量, 再通过比值法计算出样品反射率, 测量过程应保证探头视域范围内均是待测样品, 而且样品下垫面及周围环境应为全吸收材料以消除不必要的反射光, 更详细测量方法可参考文献[13]。

然后, 将式(3)组成的方程组写成形如式(2)的矩阵形式则为式(4)— 式(6)

$A_{m \times n} = [\begin{array}{l} R_{1} (λ_{1}) & \dots & R_{n} (λ_{1}) \\ ︙ & ⋱ & ︙ \\ R_{1} (λ_{m}) & \dots & R_{n} (λ_{m}) \end{array}]$ (4)

$X_{n \times 1} = [\begin{array}{l} a_{1} \\ ︙ \\ a_{n} \end{array}]$ (5)

$B_{m \times 1} = [\begin{array}{l} R_{wo} (λ_{1}) \\ ︙ \\ R_{wo} (λ_{m}) \end{array}]$ (6)

情形二, 函数f数学表达式为“ 水质遥感模型” 。以Deng模型为例, 此模型建模原理和推导过程参考文献[15, 16], 即反演水中重金属化合物的浓度。在不考虑多次散射和水底反射光的情形下, 则水中重金属浓度和离水反射率的辐射传输总方程可近似用式(7)表达

$R_{wo} (λ_{i}) = f (X_{j}) \approx \frac{P (Θ)}{4 μ} \frac{β_{w} (λ_{i}) + \sum_{j = 1}^{n} D_{j} β_{j} (λ_{i})}{k_{w} (λ_{i}) + \sum_{j = 1}^{n} D_{j} k_{j} (λ_{i})}$ (7)

式(7)中, β _j(λ _i)表示波长为λ _i的单位浓度散射系数, k_j(λ _i)表示波长λ _i的单位浓度消光系数; 下标j表示不同物质: 当j=w时, 表示该物质为水分子, 当j=1, 2, …, n时, 表示第j种重金属化合物; n为重金属化合物总数目; D_j表示待求解的第j种重金属化合物浓度; P(Θ )为散射角Θ 下的散射相函数; μ 为与观测条件有关的几何参数。

同样地, 式(7)组成方程组的矩阵形式为式(8)— 式(10)

$A_{m \times n} = [\begin{array}{l} 4 μ R_{wo} (λ_{1}) k_{1} (λ_{1}) - β_{1} (λ_{1}) P (Θ) & \dots & 4 μ R_{wo} (λ_{1}) k_{n} (λ_{1}) - β_{n} (λ_{1}) P (Θ) \\ ︙ & ⋱ & ︙ \\ 4 μ R_{wo} (λ_{m}) k_{1} (λ_{m}) - β_{1} (λ_{m}) P (Θ) & \dots & 4 μ R_{wo} (λ_{m}) k_{n} (λ_{m}) - β_{n} (λ_{m}) P (Θ) \end{array}]$ (8)

$X_{n \times 1} = [\begin{array}{l} D_{1} \\ ︙ \\ D_{n} \end{array}]$ (9)

$B_{m \times 1} = [\begin{array}{l} β_{w} (λ_{1}) P (Θ) - 4 μ R_{wo} (λ_{1}) k_{w} (λ_{1}) \\ ︙ \\ β_{w} (λ_{m}) P (Θ) - 4 μ R_{wo} (λ_{m}) k_{w} (λ_{m}) \end{array}]$ (10)

1.2 分别计算系数矩阵按列和按行相关系数矩阵

式(2)中系数矩阵A既可以写成n个列向量A_j表示, 也可以写成m个行向量A_i表示。即式(11)

$A_{m \times n} = [\begin{array}{l} A_{1} & \dots & A_{n} \end{array}] = [\begin{array}{l} A_{1} \\ ︙ \\ A_{m} \end{array}]$ (11)

式(11)中各字母意义如前所述。

不同列(或行)向量之间的线性相关程度直接决定了方程组(2)解的情况, 其原因在2.4节再作进一步剖析。在面对实际工程问题, 由于方程组里的参数值均是通过实验测量获得, 会不可避免地存在随机扰动的误差值, 不考虑自相关的情况下, 彼此间相关系数几乎不可能直接等于1, 即理论上绝对的“ 不可分” 情形不会存在。不过在某些情况下, 方程组虽可求出数值解, 但此解并不一定符合现实情况, 如丰度出现大于1或所反演重金属浓度值为负值或者异常值等。

因此, 通过分别计算彼此A_j(或A_i)的相关系数r, 从构成的相关系数矩阵, 来判断各种重金属化合物光谱结果(或波段之间)的相关程度。相关系数的计算方式可参考统计学有关理论, 这里不再赘述。

列向量A_j彼此之间生成的相关系数矩阵反映了不同重金属化合物之间的相关性, 值越高说明这两种重金属可以用线性表示彼此, 应合并作一类; 行向量A_i之间的相关系数矩阵则反映了光谱数据波段之间的相关性, 即“ 波段间冗余情况” , 在高光谱数据中经常存在波段信息冗余严重的现象。

进一步地, 把相关系数值域按等距方式划分为若干个范围后, 将矩阵里每个元素值附上对应色阶, 从而生成更加直观的二维彩色点阵图像, 即“ 相关系数热力图” 。随着波长或者重金属化合物种类数目的不断增多, 此相关系数矩阵的大小也随之增大。例如, 在波长范围350~1 050 nm内(光谱分辨率为1 nm)的不同重金属化合物反射率光谱按两两波段之间统计出的相关系数所构建的矩阵大小为701× 701, 元素总个数高达49万余个。此时用热力图表达较列出矩阵表格更直观和便于分析规律。

1.3 光谱数据重采样方法

方程里若以波长为变量的参数, 其重采样计算方法如下: 当卫星载荷波段光谱分辨率为1 nm时, 直接取与载荷中心波长最接近的波长下的参数值作为输入参数; 当其光谱分辨率大于1 nm时, 则以卫星载荷光谱响应函数作为权重, 计算载荷对应波段下的参数值加权平均值作为输入参数。以式(3)中的第j种重金属化合物反射率R_j(λ )为例, 若卫星载荷的光谱响应函数为p(λ ), 在波长范围λ ₁~λ ₂, 其反射率R'_j(λ ₁~λ ₂)用式(12)计算

$R_{j}^{\prime}\left(\lambda_{1} \sim \lambda_{2}\right)=\frac{\sum_{\lambda=\lambda_{1}}^{\lambda_{2}} R_{j}(\lambda) p(\lambda)}{\sum_{\lambda=\lambda_{1}}^{\lambda_{2}} p(\lambda)}$(12)

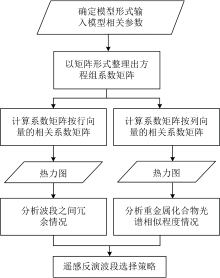
综上所述, 为便于读者理解, 整个实验方法流程, 用图1 来表示。

	Figure Option View Download New Window
	图1 实验方法流程Fig.1 Experimental method flow

2 结果与讨论

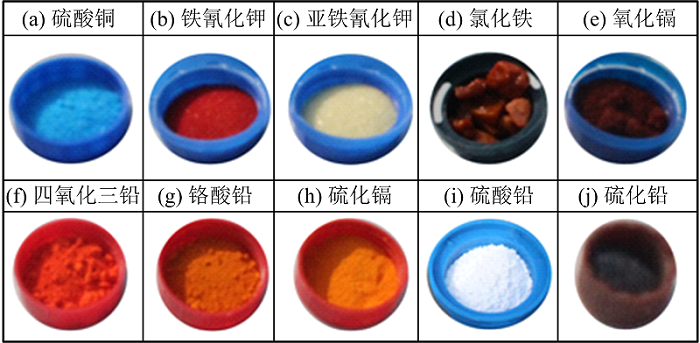
研究对象为容易引发水环境重金属污染事件的表1所列十种重金属化合物。

表1 10种重金属化合物样品真实照片 Table 1 Photos of ten kinds of heavy metal compound

2.1 铜和铁化合物的反射率光谱结果与分析

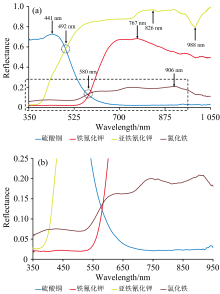
由于邓孺孺、梁业恒等前期已开展了表1所列重金属镉和铅化合物(e)— (j)的反射率测量实验, 结果与分析可参考有关文献, 如文献[13]等, 因此不再赘述。只对此次实验表1所列的铜和铁化合物(a)— (d)的反射率光谱结果进行分析和讨论。这四种化合物测量结果如图2所示。

	Figure Option View Download New Window
	图2 硫酸铜、铁氰化钾、亚铁氰化钾、氯化铁反射率光谱曲线(350~1 050 nm) (a): 全局显示; (b): 放大显示(a)虚线框区域Fig.2 The reflectance spectra of copper sulfate, potassium ferricyanide, potassium ferrocyanide, and ferric chloride (350~1 050 nm) (a): Entire wavelength range; (b): Enlarged diagram of the dashed rectangular region in Fig.2(a)

硫酸铜: 反射率从67%开始缓慢增加, 在波长441 nm出现极大值73%(也是测量波长范围中的最大值), 随后反射率快速减少。对蓝光波段有强反射, 绿光次之, 红光及近红外最弱, 反射率低于5%, 可见光反射率测量结果与化合物本身呈现水蓝色吻合。

氯化铁: 反射率从6%“ 波浪式” 缓慢增加至最大值21%(位于波长906 nm)后开始缓慢减少至11%结束, 测量波长范围内整体反射率不高, 对红光反射相对蓝绿光稍高, 因而呈现棕褐色。

铁氰化钾: 在蓝绿光波段内, 反射率低于4%, 随后在红光波段内快速增大至60%以上, 在波长767 nm出现极大值68%(测量波长范围中的最大值), 随后开始减少, 整体对红光至近红外波段有强反射, 与化合物呈现暗红色吻合。

亚铁氰化钾: 紫光波段低反射, 随后从蓝光波段开始反射率快速增加, 对绿光和红光均有强反射, 与化合物呈现浅黄色吻合。从红光波段开始反射率增速放缓, 但仍持续增加, 在波长826 nm出现极大值97%(测量波长范围最大值), 随后反射率开始减少, 在波长988 nm有一极小值80%, 然后又开始增大。

此外, 留意这四种化合物反射率光谱的两个“ 交点” 位置。波长位置1: 硫酸铜和亚铁氰化钾在波长492 nm相交(反射率为58%); 波长位置2: 硫酸铜、氯化铁、铁氰化钾三者相交于在波长范围576~584 nm(中心波长580 nm, 位于绿光波段), 反射率为13%~14%。

由于光谱曲线交点处正是两条曲线此消彼长开始的特殊位置, 如果存在两个这样的交点, 那么很容易通过波段比值运算大大增强二者之间的差异性。例如仿效比值植被指数Ratio Vegetation Index(RVI), 如果大胆地猜想存在这样一个“ 比值铜指数Ratio Copper Index(RCI)”

$RCI = \frac{R (λ = 492 nm)}{R (λ = 580 nm)}$ (13)

硫酸铜的RCI会大于1, 而三种铁化合物RCI均小于1, 那么经过式(13)的光谱处理后, 增强硫酸铜信息量同时又抑制了这三种铁化合物中的信息量, 从而将硫酸铜从中区分开来。但RCI有局限性: 只对硫酸铜和这三种铁化合物之间的可分性适用。

2.2 不同光谱分辨率下重金属化合物光谱之间相关性变异分析

为了适应将来卫星层面的水体重金属遥感研究需要, 除了原始光谱仪数据外, 额外选择我国三颗卫星的载荷, 根据其波谱设计参数, 利用式(12)对原始光谱仪数据进行相应波段的重采样处理, 分析不同光谱分辨率下的相关系数矩阵变异规律。载荷信息如表2所列。

表2 用于计算相关系数矩阵的四种光谱分辨率设置表^* Table 2 Four kinds of spectral resolution settings for calculating the correlation matrix^*

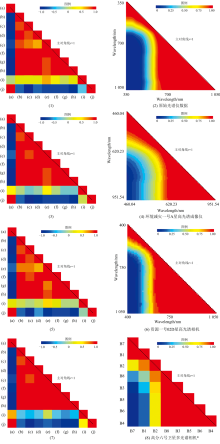
根据1.2节的方法, 以1.1节情形一的“ 混合像元信息线性分解模型” 为例, 得到图3的相关系数热力图。图3中的子图(1)、 (3)、 (5)和(7)为不同重金属化合物在表2所列不同光谱分辨率情形下, 即按式(4)的系数矩阵列向量计算彼此的相关系数, 这四个分图中的行列标示(a)— (j)代表的化合物和表1所列一致, 为了读者便于阅读, 正文书写化合物名称时, 带上前面字母序号(下同); 这四个分图所示矩阵大小均为10× 10。图3中的子图(2)、 (4)、 (6)和(8)为对应左侧分图按不同波段, 即按式(4)的系数矩阵行向量计算彼此的相关系数。从图3可以发现如下规律:

Figure Option
View Download New Window

图3 相关系数热力图
(1)、 (2): 原始光谱数据; (3)、 (4): 环境减灾一号A星高光谱成像; (5)、 (6): 资源一号02D星高光谱相机; (7)、 (8): 高分六号卫星多光谱相机^*注: * 分图3(8)中行列标号表示的波长范围为: B7: 400~450 nm; B1: 450~520 nm; B2: 520~590 nm; B8: 590~630 nm; B3: 630~690 nm; B5: 690~730 nm; B6: 730~770 nm; B4: 770~890 nmFig.3 Correlation coefficient heatmaps
(1), (2): Raw spectral data; (3), (4): Hyperspectral imager (HSI) on China HJ-1A satellite; (5), (6): Advanced hyperspectral imager (AHSI) on China ZY-1E satellite; (7), (8): Wide-field-view (WFV) camera on China GF-6 satellite^*Note: * The wavelength ranges in Fig.3 (8) are: B7 (400~450 nm); B1 (450~520 nm); B2 (520~590 nm); B8 (590~630 nm); B3 (630~690 nm); B5 (690~730 nm); B6 (730~770 nm); B4 (770~890 nm)

首先, 图3展示的热力图中除了自相关这种特例(即矩阵主对角线上)相关系数等于数值1外, 其余元素彼此均没有出现此现象, 这和1.2节提到的“ 面对实际工程问题不存在数学上绝对不可分的情形” 这一推论相吻合。

进一步地, 由图3左侧四个子图可以发现: 总体上, 这十种重金属化合物的相关程度有明显区别, 色调趋于冷色调(蓝色)则表示彼此的反射率光谱形状相反(负相关), 色调趋于暖色调(红色)则表示彼此反射率光谱形状相似(正相关)。以(a)硫酸铜为例, 在原始1 nm光谱分辨率下, (a)硫酸铜和除了(j)硫化铅外的其余八种化合物有非常好的可分性, 这也说明了2.1节中(a)硫酸铜较容易设计“ 比值指数” 来增强和其他化合物光谱差异性的原因。另一方面, 随着光谱分辨率变化, (a)硫酸铜与其他化合物可分性也发生变化, 其中变化最为明显的是和(i)硫酸铅的可分性, 相关系数最高出现在光谱分辨率最低的高分六号载荷上, 此时可分性明显降低; 在其余三种分辨率下均接近于0, 表示其可分性较好。

此外还发现有部分化合物可分性并不和光谱分辨率变化保持一致单调性, 当光谱分辨率处于某个适当的取值时, 其相关系数可达最低, 例如, 化合物(g)铬酸铅和(d)氯化铁在以资源一号02D星的光谱分辨率时, 相关系数相对最低, 可分性相对提升。这现象揭示了可分的过程要考虑彼此的光谱整体差异性, 这种差异性往往不能单靠某个“ 指纹” 特征谱线所决定的, 而是需要多个波长组成的“ 光谱曲(折)线” 。这恰恰印证了未来需要不断充实“ 连续光谱” 光学参数库的必要性和重要性。

特别地, 在图3(8)高分六号卫星载荷波谱设置可知, 其波段数已小于化合物总数了, 此时, 方程组必然没有唯一数值解, 需要从图3(7)中, 剔除至少两种化合物。显而易见地, 按图3(7)中相关系数从大到小, 按照“ 二选一” 原则剔除, 最终令化合物总数不大于波段数。例如, (h)硫化镉和(g)铬酸铅; 再如(d)氯化铁和(f)四氧化三铅。值得注意的是, 剔除后化合物数目发生了变化, 因此所对应的按波段统计的热力图应重新生成, 因为式(4)的系数矩阵的行向量元素变少了, 相关系数也会随之联动变化。

受篇幅限制, 其余种种化合物的可分性不能一一展开讨论。图3所展示的热力图反映了这十种重金属化合物之间很多有价值的可分性参考依据。

2.3 遥感反演波段选择的策略

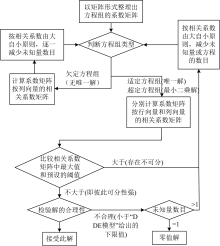
由2.2节不同情形下得到的相关系数热力图可以发现, 重金属化合物数目和参与遥感模型实施反演的波段数目, 是一个动态调整的过程: 最终要将一个初始可能是“ 病态” 的方程组转化成能求解得到合理数值解的“ 有效” 方程组。因此提出下面波段选择的策略:

当遥感模型按式(2)的矩阵形式整理完毕后, 第一步, 按化合物种类最大数目和所有联立方程组的方程最大数目, 先分别计算出初始相关系数矩阵。若此时, 方程组系数矩阵在此情况下, 化合物彼此的相关系数已处于较低, 例如均不大于预设的相关系数阈值r_m。那么可直接进行下一个环节: 判断方程组类型。

在判断方程组类型环节, 若未知量数目等于方程数, 则方程组为适定方程组, 得唯一解。再进行下一个环节: 检验解的合理性。通过文献[8]提出的遥感敏感性分析模型(简称“ DDE模型” ), 比较此解数值是否不小于下限浓度值。若满足, 则接受此唯一解。

若未知数小于方程数, 则方程组为超定方程组, 可得最小二乘解。同样地, 按照上步检验解的合理性。若满足, 则接受此最小二乘解。

若未知数大于方程数, 则方程组为欠定方程组, 则需要按照相关系数(按化合物种类统计)由大自小的顺序, 逐一减少化合物种类数目。直至方程组类型为适定或超定方程组。随后分别重新计算按列和行的相关系数矩阵, 重新回到第一步, 周而复始。

若不满足解的合理性, 则按照相关系数由大至小原则, 减少化合物种类或波段数目。只要化合物种类和波段数目二者之一发生了改变, 都需要重新分别计算出新的系数矩阵按行(即按波段)和按列(即按重金属化合物种类)的相关系数矩阵。然后, 重新回到第一步, 周而复始。

直到化合物种类数目或波段数目减少至一个。此时, 认为待反演的像元信息, 不足以反演(或者并不含有)待求的化合物, 方程组无合理数值解, 则人为给予“ 零值解” 。

整个波段与化合物种类动态筛选流程, 用图4表示更为直观。

	Figure Option View Download New Window
	图4 遥感模型求解流程示意图Fig.4 Schematic diagram of remote sensing model solution process

2.4 重金属光谱可分性所揭示的数理意义

之所以重视重金属光谱可分性的内在数理意义, 是因为最终面对的是要解决涉及多参数的遥感模型求解问题。

从数学角度看, 根据线性代数理论, 若式(2)、式(4)和式(8)中系数矩阵A的秩小于待求重金属化合物数目n, 那方程组(2)有无穷多个解, 其实就意味着这些化合物之间存在不可分(或部分不可分)的情形; 反之, 则可分。所以, 重金属化合物之间能否可分, 便转化为方程组(2)的解向量(5)或(9)存不存在合理的数值解这一数学问题。

从物理学角度看, 实际上式(11)每个列向量A_j可视作第j种重金属化合物在方程组(2)里的各个方程(1)的系数随波长变化的光谱曲线。情形一中, 式(4)列向量A_j等价于各种重金属化合物的反射率光谱曲线; 情形二中, 式(8)A_j不再是单纯的某个表观光学物理量, 而是某个水质遥感模型(如Deng模型)经过数学整理后得到关于重金属化合物的方程系数随波长变化的“ 光谱结果” , 相比情形一更为复杂, 但可以反演的目标变量是更深层次的浓度值。另一方面, 式(11)每个行向量A_i对应的是光谱数据根据每个波长所建立方程(1)或方程(3)或方程(7)整理后的关于所有化合物未知量的系数数组。

那么, 重金属在某种光谱数据集中能否可分, 其数理本质应满足这个目标: 波段之间和化合物之间的线性相关程度同为最低的情况下, 得到的方程数目应不少于待求未知数, 亦即所联立方程组应为“ 适定方程组” 或“ 超定方程组” 。

3 结论

开展了波长范围350~1 050 nm的硫酸铜、铁氰化钾、亚铁氰化钾和氯化铁的反射率测量, 对光谱结果进行分析和讨论; 然后, 对含铜、铁、镉、铅元素的十种重金属化合物反射率光谱, 分析彼此之间按化合物种类和波段数目的相关系数热力图; 给出一种未来水体重金属遥感反演波段选择的策略。得出如下结论与展望:

(1)继续扩充连续波长下的反射率光谱等光学参数库非常必要, 相比以前只关注重金属的某个“ 指纹” 特征谱线, 现在连续光谱结果更像是它们的“ DNA” , 信息量更为全面。可为更复杂的遥感模型提供基础参数, 有助于开展类似模型求解算法剖析、敏感性分析等更深入的方面研究。

(2)借助相关系数热力图, 可以更好揭示不同重金属化合物光谱可分性的数理本质, 也一定程度说明了光谱分辨率和化合物种类数目二者共同决定了方程组解的情况。并不能简单地认为光谱分辨率越高可分性就越高, 而是取决于重金属化合物彼此间在某个光谱分辨率下所形成的光谱函数形状的差异程度。

(3)最后基于相关性热力图给出了一个未来进行水体重金属浓度遥感模型求解的算法理论框架, 是突破其卫星反演瓶颈的关键技术, 是为了进一步打下求解更复杂遥感物理分析模型的算法基础。下一阶段, 将由讨论反射率等基础光谱相似度, 深入至更广义的遥感模型所构建起的方程组系数矩阵的相似度, 达至求解出模型合理数值解, 以实现其卫星影像层面的遥感反演这一最终目标。

参考文献

文献列表

[1]	Liu X P, Huang Y H, Xu X C, et al. Nature Sustainability, 2020, 3: 564. [本文引用:1]
[2]	He D, Shi Q, Xue J Q, et al. Remote Sensing of Environment, 2023, 299: 113884. [本文引用:1]
[3]	ZHANG Zhi-xin, DENG Ru-ru, LI Hao, et al(张志新, 邓孺孺, 李灏, 等). Remote Sensing for Land and Resources(国土资源遥感), 2011, (3): 88. [本文引用:2]
[4]	HE Ying-qing, QIN Yan, FU Qing-hua, et al(何颖清, 秦雁, 扶卿华, 等). Tropical Geography(热带地理), 2016, 36(5): 860. [本文引用:2]
[5]	Yang J Y, Deng R R, Ma Y W, et al. Sensors, 2025, 25(6): 1728. [本文引用:1]
[6]	Yang J Y, Deng R R, Ma Y W, et al. Water, 2025, 17(6): 780. [本文引用:1]
[7]	Qiao H Y, Lee Z P, Wang D S, et al. Remote Sensing of Environment, 2025, 323: 114709. [本文引用:1]
[8]	Guo Y, Liang Y H, Deng R R, et al. Heliyon, 2022, 8(12): e12033. [本文引用:2]
[9]	LIU Zhi-fei, YANG Xue-mei, WANG Jing-rui, et al(刘志飞, 杨雪梅, 王景瑞, 等). Arid Zone Research(干旱区研究), 2025, 42(1): 141. [本文引用:1]
[10]	MENG Chang, HONG Mei, LI Fei(孟畅, 红梅, 李斐). Ecology and Environmental Sciences(生态环境学报), 2025, 34(6): 950. [本文引用:1]
[11]	Wang L, Zhou Y, Zhou Z H, et al. IEEE Transactions on Geoscience and Remote Sensing, 2025, 63: 4504714. [本文引用:1]
[12]	DENG Ru-ru, LIANG Ye-heng, GAO Yi-kang, et al(邓孺孺, 梁业恒, 高奕康, 等). National Remote Sensing Bulletin(遥感学报), 2016, 20(1): 35. [本文引用:2]
[13]	LIANG Ye-heng, OUYANG Yu-chun, XU Min-duan, et al(梁业恒, 欧阳宇纯, 许敏端, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2025, 45(8): 2149. [本文引用:4]
[14]	LIANG Ye-heng, DENG Ru-ru, GAO Yi-kang, et al(梁业恒, 邓孺孺, 高奕康, 等). National Remote Sensing Bulletin(遥感学报), 2016, 20(1): 27. [本文引用:1]
[15]	DENG Ru-ru, HE Zhi-jian, CHEN Xiao-xiang, et al(邓孺孺, 何执兼, 陈晓翔, 等). Acta Scientiarum Naturalium Universitatis Sunyatseni(中山大学学报·自然科学版), 2002, 41(3): 99. [本文引用:1]
[16]	Deng R R, Liu Q H, Ke R P, et al. Acta Oceanologica Sinica, 2004, 23(1): 119. [本文引用:1]

2020

0.0

... 随着载荷探测光谱分辨率不断提升, 遥感可反演参数越来越丰富, 如亚像元级别的城市土地利用/土地覆盖分类、城市变化^[1,2]、植被覆盖度^[3,4], 水质遥感方面的悬浮泥沙、叶绿素a、有机污染物浓度等^[5,6,7] ...

2023

0.0

2011

0.0

... , 具体建模原理参见文献[3,4] ...

2016

0.0

... , 具体建模原理参见文献[3,4] ...

2025

0.0

2025

0.0

2025

0.0

2022

0.0

... 随着高光谱影像的出现, 以往一直备受质疑遥感反演可行性的水体重金属也有了提取潜力^[8] ...

... 通过文献[8]提出的遥感敏感性分析模型(简称#cod#x0201c ...

2025

0.0

... )、主成分分析、导数光谱等是较常用评价指标^[9], 提取不同物质的#cod#x0201c ...

2025

0.0

... 由于提取特征的方法和指标多样, 学者开始结合机器学习、神经网络、分层建模等自动寻优方法^[10,11] ...

2025

0.0

... 由于提取特征的方法和指标多样, 学者开始结合机器学习、神经网络、分层建模等自动寻优方法^[10,11] ...

2016

0.0

... 氯化铁和铁氰化钾, 广泛用于建筑、染料和冶金工业^[12] ...

... 这些化合物在作者前期开展的光学参数测量实验结果中, 已发现其在可见光-近红外波段具有特征光谱响应^[12,13,14], 从而会导致重金属污染水体的反射或吸收光谱与正常水体产生差异性 ...

2025

0.0

... 镉和铅化合物(如硫化镉、铬酸铅), 主要通过电镀、电池制造废水进入自然水体^[13] ...

... 选择干燥晴天, 利用光谱仪分别对标准板和样品进行辐亮度测量, 再通过比值法计算出样品反射率, 测量过程应保证探头视域范围内均是待测样品, 而且样品下垫面及周围环境应为全吸收材料以消除不必要的反射光, 更详细测量方法可参考文献[13] ...

... (j)的反射率测量实验, 结果与分析可参考有关文献, 如文献[13]等, 因此不再赘述 ...

2016

0.0

2002

0.0

... 以Deng模型为例, 此模型建模原理和推导过程参考文献[15,16], 即反演水中重金属化合物的浓度 ...

2004

0.0

... 以Deng模型为例, 此模型建模原理和推导过程参考文献[15,16], 即反演水中重金属化合物的浓度 ...