GMI/GF-5B观测的是地表反射的超分辨率太阳光谱, 包含近红外(near infrared, NIR)和短波红外(short wave infrared, SWIR-1、 SWIR-2、 SWIR-3)共四个观测波段, 中心波长分别为0.76、 1.58、 1.65、 2.0 μ m^[13]。 其中CO₂和CH₄分别在1.58和1.65 μ m近红外波段附近有明显的吸收特征, 因此分别使用该波段高光谱观测数据来反演大气CO₂和CH₄的垂直干空气混合比柱浓度(XCO₂和XCH₄), 训练中选择的光谱范围分别为6 320~6 370和6 040~6 090 cm^-1。 另外, 在全球范围选择6个TCCON站点Garmisch(Germany)、 Izana(Spain)、 Saga(Japan)、 Ny-Å lesund(Norway)、 Park Falls(USA)和Wollongong(AU), 将这6个站点在2016年— 2021年之间的大气廓线输入SCIATRAN, 分别模拟构建6 000条卫星观测光谱, 并将模拟光谱与太阳天顶角、 温度、 压强等影响因子共同构成1DCNN 的输入特征, 并将TCCON观测XCO₂和XCH₄作为1DCNN的输出对比结果。 考虑到样本集中输入特征的尺度不同, 也为了避免训练时出现过拟合或欠拟合等情况, 实验中又对输入特征进行了最大最小值归一化处理, 使得归一化后的输入特征具有相似的数据分布, 从而提高模型的泛化能力^[14]。 归一化公式如式(1)

G=(Gmax-Gmin)×(T-Tmin)Tmax-Tmin+Gmin(1)

式(1)中, T表示训练样本的初始值, G和T表示归一化后的值; T_max和T_min为最大和最小值; G_max和G_min分别为G的最大和最小值, 本文采用1和-1。 基于上述的数据归一化处理, 本文分别构建了XCO₂和XCH₄的5 000个训练样本集和1 000个测试样本集。

机器学习是人工智能的一个分支, 利用数据、 算法和统计学习的原理, 使计算机能够自动学习并改进其性能的一种方法。 机器学习能够预先完成建模中耗时的部分, 克服了辐射传输模型中复杂的物理计算和星载传感器的观测精度以及观测地理环境的限制^[15]。 常见的机器学习方法包括决策树、 随机森林、 神经网络和支持向量机等。 一维卷积神经网络(1DCNN)是专门用于处理一维序列数据的机器学习方法, 具有局部连接、 权值共享、 计算简单等特点, 已广泛用于处理卫星遥感数据。 考虑到卫星观测光谱的一维序列特征, 1DCNN建立短波红外通道卫星温室气体浓度反演模型。 1DCNN由输入层、 一维卷积层、 激活层、 池化层、 全连接层和输出层组成^[16]。 其中, 卷积层是卷积网络中最重要的一层, 它利用卷积核扫描输入数据进行加权求和, 提取输入数据的局部特征。 卷积之后, 通常会加入偏置并引入激活函数。 激活函数对卷积层输入的特征值进行非线性变换, 限制输出特征值的范围, 从而增加1DCNN的非线性拟合能力^[17]。 为了避免在特征学习过程中出现梯度消失, 帮助网络模型更快地收敛, 将所有激活函数均设置为校正线性单元(rectified linear unit, ReLU), 并采用最大池化降采样处理特征值, 最后将经过卷积、 激活和池化后的计算结果输送到全连接层进行线性变换, 并将最终预测结果传送到输出层。

训练卷积神经网络需要动态调整各层神经元之间的网络参数(连接权重和偏置), 并找到一组最优的超参数, 从而提高网络的预测性能和准确度。 在训练过程中, 主要使用自适应矩估计(adaptive moment estimation, Adam)和贝叶斯优化(Bayesian optimization, BO)两种算法。 Adam是一种自适应学习率的机器学习优化算法, 它结合了Momentum和RMSprop算法的优点, 主要解决梯度消失和梯度爆炸问题, 特别适用于大规模数据集和高维空间的参数更新^[18]。 该算法采用链式求导的方式计算损失函数相对于网络参数的梯度。 计算梯度的一阶矩估计平滑处理梯度方向, 可以加快算法的收敛速度。 计算梯度的二阶矩估计为每个网络参数分配不同的学习率, 反映网络参数更新的变化程度。 通过更新梯度的一阶矩估计和二阶矩估计, 使其适应不同的数据特征和训练阶段, 以实现损失函数的最小化, 确保网络的输出结果无限逼近于观测的目标值。 BO算法是一种高效的全局优化方法, 特别适用于优化计算成本较高的黑盒函数。 在卫星温室气体浓度反演中, 1DCNN的超参数优化就是一个典型的黑盒优化问题, 因为超参数的性能评估通常需要大量的计算资源。 BO算法利用已有的搜索点及其函数值等先验信息, 通过高斯过程构建代理模型, 不断逼近目标函数, 并预测目标函数值的均值和方差, 从而确定预测值的置信区间^[19]。 在每次迭代中, BO算法根据代理模型的预测值选择下一个最有希望的超参数组合, 在实际的目标函数上评估该搜索点的性能, 并将新的评估结果加入到先验信息中, 更新代理模型。 在选择下一个搜索点时采集函数会探索不确定区域寻找潜在的最优解或利用已知具有较好目标值的区域进行优化, 当达到预设的迭代次数或代理模型的预测精度不再显著提升时, 优化过程终止, 并确定一组最优超参数。 采用机器学习框架定义1DCNN的超参数搜索空间, 包括学习率、 训练周期、 批量大小、 卷积核数量、 卷积核大小、 网络层数和激活函数等, 并确定每一个超参数的搜索范围, 如表1所示。

表1

Table 1

表1(Table 1)

表1 1DCNN超参数的设置 Table 1 Hyperparameter settings of 1DCNN 参数 取值范围 参数描述 学习率(learning rate) [1× 10-3, 1× 10-4, 1× 10-5] 控制每次权重和偏置值的更新步长 训练周期(epoch) [200, 400, 600, 800, 1 000] 模型使用整个数据集进行一次训练的过程 批量大小(batch size) [16, 32, 64, 128] 模型进行一次迭代训练使用的样本数 卷积核数量(kernel number) [2, 4, 6] 不同卷积核从输入序列中提取不同特征 卷积核大小(kernel size) [3, 5, 7, 9, 11] 卷积操作中与原始输入序列进行加权求和 网络层数(layer number) [3, 4, 5] 卷积层、池化层和全连接层的数量 激活函数(activation function) [ReLU, Sigmoid] 非线性变换特征, 限制输出值范围

表1 1DCNN超参数的设置 Table 1 Hyperparameter settings of 1DCNN

采用决定系数(R²)作为超参数的评价指标, 通过选择一组最优的超参数衡量机器学习方法的预测性能, 即机器学习方法拟合数据的程度, R²越接近1, 机器学习方法预测越准确, 拟合效果越好^[20]。 计算公式如式(2)

R2=1-∑i(yi-ŷi)2∑i(yi-y̅2)(2)

式(2)中, y_i表示观测值, ŷi表示预测值, y̅表示平均值。

利用构建好的5 000个训练样本集和1 000个测试样本集以及两种机器学习优化算法, 训练基于1DCNN的卫星温室气体浓度反演模型。 其中, 1DCNN采用信号前向传播和误差反向传播的方式进行迭代训练, 以优化超参数并提高反演模型对温室气体浓度的预测精度, 训练过程中的最优超参数设置如表2所示。

表2

Table 2

表2(Table 2)

表2 1DCNN最优超参数的设置 Table 2 Hyperparameters setting of 1DCNN 训练超参数 设置值 学习率(learning rate) 1× 10-5 训练周期(epoch) 800 批量大小(batch size) 64 卷积核数量(kernel number) 4 卷积核大小(kernel size) 9 网络层数(layer number) 3 激活函数(activation function) ReLU

表2 1DCNN最优超参数的设置 Table 2 Hyperparameters setting of 1DCNN

在信号前向传播阶段, 使用随机数初始化1DCNN的网络连接权重, 将卫星模拟光谱等输入特征依次通过卷积层、 激活函数、 池化层和全连接层进行计算, 并将最终的计算结果作为1DCNN的预测值传送到输出层。 在误差反向传播阶段, 比较1DCNN输出层的预测值与TCCON实际观测值, 计算平均绝对误差(mean absolute error, MAE)作为损失函数, 用于量化预测值与观测值之间的差异, 计算公式如式(3)。 通过将损失函数对网络连接权重的梯度逐层反向传播, 更新1DCNN的网络连接权重。

MAE=1n∑i=1n|yi-ŷi|(3)

式(3)中, y_i表示观测值, ŷi表示预测值, n表示样本数量。

通过训练周期控制机器学习模型迭代训练的停止条件, 并以测试样本集的最大R²作为若干训练周期中最好的训练结果。 一个训练周期是将所有数据分为若干批次全部输入网络中完成一次信息正向计算和误愁反向传播的过程^[21]。 同时, 从构建好的XCO₂和XCH₄样本集中训练并测试基于1DCNN的卫星温室气体浓度反演模型, 其训练R²与测试R²随着训练周期的变化趋势如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 XCO2和XCH4样本集训练R2 (a)和测试R2 (b)的曲线图Fig.1 Curves of training R2 (a) and test R2 (b) of XCO2 and XCH4 sample set

从R²的变化趋势可知: 当训练周期设置为800轮次时, XCO₂和XCH₄样本集的训练R²和测试R²均达到最大值, 并将测试样本集中卫星反演XCO₂和XCH₄与TCCON观测数据进行回归拟合, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于1DCNN的卫星反演XCO2和XCH4与TCCON观测XCO2和XCH4的拟合Fig.2 Fitting of satellite inversed XCO2 and XCH4 based on 1DCNN to TCCON observed XCO2 and XCH4

为了进一步验证基于1DCNN的卫星温室气体浓度反演模型的预测性能, 又基于随机森林(random forest, RF)和反向传播神经网络(backpropagation neural network, BPNN)两种机器学习方法进行模型的训练以及模型性能的测试。 其中, RF是基于决策树的集成学习算法, 依赖手动特征工程, 无法自动提取卫星光谱的局部的特征, 在高维、 序列化的光谱数据中表现不足。 BPNN是基于前馈神经网络的全连接网络, 参数多, 容易过拟合, 而且对局部特征不敏感。 RF和BPNN都是传统的机器学习方法, 属于浅层的统计学习模型。 1DCNN基于数据驱动学习模型, 属于深度神经网络, 能够利用卷积核自动提取光谱的局部特征, 更加适合处理卫星数据。 将RF和BPNN在测试样本集上的预测结果与TCCON观测结果进行回归拟合, 如图3所示。 从拟合结果的离散程度可知, 与1DCNN相比, 基于RF和BPNN的卫星反演结果与TCCON观测数据的离散程度高且相关性较低, 从而表明了基于1DCNN的卫星温室气体浓度反演模型在预测XCO₂和XCH₄方面具有更好的性能。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 基于RF/BPNN的卫星反演XCO2和XCH4与TCCON观测XCO2和XCH4的拟合Fig.3 Fitting of satellite inversed XCO2 and XCH4 based on RF/BPNN to TCCON observed XCO2 and XCH4

为了更直观的分析CO₂和CH₄在全球范围内的分布情况, 利用基于1DCNN的卫星温室气体浓度反演模型, 从2021年9月7日发射的高分五号B卫星主要温室气体监测仪(GMI/GF-5B)高光谱观测数据中反演2022年— 2024年全球XCO₂和XCH₄, 如图4和图5展示了CO₂和CH₄的年均值分布。 其中, 由于卫星数据发布等原因, 2024年的XCO₂和XCH₄反演结果只包含1月— 8月。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 2022年— 2024年全球CO2年均值Fig.4 Annual global CO2 average in 2022— 2024

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 2022年— 2024年全球CH4年均值Fig.5 Annual global CH4 average in 2022— 2024

从全球XCO₂和XCH₄的年均值反演结果可以看出: 中纬度地区的XCO₂和XCH₄明显高于低纬度地区和高纬度地区。 同时, 2023年和2024年的XCO₂和XCH₄明显高于2022年, 全球XCO₂和XCH₄也在逐年升高。

GMI/GF-5B遥感测点与TCCON站点难以从空间上完全匹配, 实验中对数据的匹配需从时间、 空间和数据匹配量上进行综合考虑。 验证过程中, 选择TCCON站点中心经纬度± 2.5° 范围内, GMI/GF-5B过境时间前后1 h的数据进行时空匹配^[22]。 TCCON站点的观测数据更新会有延迟, 且目前共有28个站点在运行。 考虑到TCCON站点的空间分布和观测时间以及每个站点观测数据的更新进度, 选择目前已经更新到2022年— 2024年的观测数据且时空匹配后数据样本较多的9个站点, 如表3所示, 并统计了每个站点数据样本的平均绝对误差(MAE)。

表3

Table 3

表3(Table 3)

表3 验证反演结果的TCCON站点 Table 3 TCCON site to verify inversion results Site Name Latitude, Longitude/(° ) MAE(XCO2)/ppm MAE(XCH4)/ppb California(USA) (34.14N, -118.13E) 1.129 5 8.580 6 Edwards(USA) (34.96N, -117.88E) 1.096 1 8.252 5 East Trout Lake(Canada) (54.35N, -104.99E) 1.080 5 8.169 1 Harwell(UK) (51.57N, -1.32E) 1.103 7 8.493 6 Karlsruhe(Germany) (49.1N, 8.44E) 1.070 1 8.146 6 Burgos(Philippines) (18.53N, 120.65E) 1.097 8 8.279 6 Nicosia(CY) (35.14N, 33.38E) 1.091 8 8.215 4 Lamont(USA) (36.6N, -97.49E) 1.140 6 8.731 6 Paris(FR) (48.85N, 2.36E) 1.182 4 9.079 5

表3 验证反演结果的TCCON站点 Table 3 TCCON site to verify inversion results

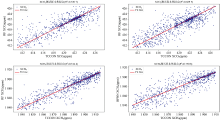
对比分析2022年— 2024年基于1DCNN的卫星反演XCO₂和XCH₄与TCCON观测XCO₂和XCH₄来验证基于1DCNN的卫星温室气体浓度反演模型的有效性, 验证结果如图6— 图9所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 2022年— 2024年基于1DCNN的卫星反演XCO2与TCCON观测XCO2的拟合Fig.6 Fitting of satellite inversed XCO2 based on 1DCNN to TCCON observed XCO2 in 2022— 2024

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 2022年— 2024年基于1DCNN的卫星反演XCO2的误差绝对值和误差百分比Fig.7 Absolute error and percentage error of satellite inversed XCO2 based on 1DCNN in 2022— 2024

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 2022年— 2024年基于1DCNN的卫星反演XCH4与TCCON观测XCH4的拟合Fig.8 Fitting of satellite inversed XCH4 based on 1DCNN to TCCON observed XCH4 in 2022— 2024

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 2022年— 2024年基于1DCNN的卫星反演XCH4的误差均对值和误差百分比Fig.9 Absolute error and percentage error of satellite inversed XCH4 based on 1DCNN in 2022— 2024

从图6— 图9可以看出, 2022年— 2024年基于1DCNN的卫星反演XCO₂和XCH₄与TCCON观测XCO₂和XCH₄均表现出较高的相关性和一致性。 从不同站点的拟合结果和误差分析可以发现, 反演模型的预测性能在不同区域存在一定差异。 尤其是Harwell站点, XCO₂和XCH₄的验证R²分别达到了0.960 6和0.986 8。 Harwell位于北欧, 所处环境相对简单, 而且受工业等人为活动的影响较小, 因此具有较好的反演精度。 另外, 通过统计验证数据中卫星反演XCO₂和XCH₄与TCCON观测XCO₂和XCH₄之间的误差发现, 99.15%的XCO₂误差在1.5 ppm以内, 0.85%的误差在1.5~2 ppm范围内; XCH₄的误差在10 ppb范围内。 验证结果表明: 本文提出的基于1DCNN的反演模型在GMI/GF-5B温室气体浓度反演中具有较高的精度, 也进一步证明了该反演模型的有效性。