2.1.1 显著性算法应用基础

目前, 应用到图像处理的显著性算法主要有四种, 分别是: Local Contrast显著性算法, 计算某个像素在整个图像上的全局对比度, 即该像素与图像中其他所有像素在颜色上的距离之和作为该像素的显著值^[13]; Frequency-turned显著性算法, 从频率角度分析图像, 图像在频率域可以分成低频部分和高频部分。 低频部分反映了图像的整体信息, 显著性区域检测用到的更多的是低频部分的信息; Histogram-based Contrast显著性算法, 基于区域比较的视觉显著性检测算法, 该方法基于颜色全局直方图计算像素点与其他像素之间的颜色特征差异, 差异度越大显著性越高; Spectral Residual显著性算法, 基于信息论的角度, 将图像分为突出信息和冗余信息, 通过在对数谱中用原图像的信息减去冗余信息, 即可获得显著目标的对数谱。 该算法首先对图像进行傅里叶变换, 将局部平滑的对数幅度谱作为冗余部分, 然后用原对数谱减去平滑后的对数幅度谱, 那么剩余的部分就是显著区域在频域中的信息, 最后通过傅里叶逆变换, 从频域变化到空域生成显著图。

表2

Table 2

表2(Table 2)

表2 常见显著性算法 Table 2 Common saliency algorithms 显著性算法 计算公式 原理 Local Contrast S(p)=∑q∈Id(p, q) 计算某个像素在整个图像上的全局对比度。 Frequency-turned S(x, y)=‖Iμ-Iwch(x, y)‖ 从频率角度分析图像, 利用低频信息进行显著性区域检测。 Histogram-based Contrast S(x, y)=∑(i, j)∈D‖I(x, y)-I(i, j)‖ 基于区域比较, 差异度越大显著性越高。 Spectral Residual S(x)=[iFFT(exp(R(f)+iP(f)))2]* G(x) 基于信息论, 通过傅里叶逆变换, 从频域变化到空域生成显著图。

表2 常见显著性算法 Table 2 Common saliency algorithms

提取高光谱图像源的某一波段进行显著性算法处理得到如图1所示。 其中, 图1(a)是高光谱数据的第10波段原始数据, 图1(b)为结合奥维地球目视判读并通过图像处理技术得到的二元地面真值(ground-truth, GT)图, 主要呈现建筑用地的实际分布位置。 图1(c— f)分别展现了采用LC、 FT、 HC、 SR显著性算法得到的显著图。 显著图中背景区域受到抑制, 表现为深暗色调, 显著像元聚集成簇高亮显示, 成为图像中的显著区域。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 波段10、 GT图及显著图(a): Band10; (b): Ground-truth; (c): LC; (d): FT; (e): HC; (f): SRFig.1 Band 10, GT maps and saliency maps(a): Band10; (b): Ground-truth; (c): LC; (d): FT; (e): HC; (f): SR

2.1.2 显著性检测波段效果评价

引入视觉显著性模型对特定高光谱波段进行显著目标的增强, 可以将图像中的显著地物目标提取出来。 经过大量实验, 结合珠海一号高光谱数据在各自子空间内相关性均比较强, 且波段数目相对较少, 采取四种显著性算法得到的最佳显著性波段具有较强的一致性, 如果分别采取四种方法对各个数据源进行实验, 这无疑会增加时间复杂性, 对结果的准确性也会产生一定影响。

本节引入视觉显著性检测指标中的平均绝对误差(mean absolute error, MAE)评价各显著性算法的检测效果, 并最终选取最佳的显著性算法。

评测指标MAE用来估算预测值与真值之间的一致性, 其值越小表示预测模型越好, 表达式为

MAE=1W×H∑x=0W∑y=1H|P(x, y)-Y(x, y)|(1)

式(1)中, W和H分别代表特征图的宽度和长度, P(x, y)表示预测图P中(x, y)处的像素值, Y(x, y)表示真值图Y中(x, y)处的像素值。 预测图P和真值图Y中的每一个像素值都需要被归一化到区间[0, 1]。

为了选出最佳的显著性检测算法, 采取计算机视觉中常用的大津法对图像进行二值化处理, 大津法属于自适应阈值的方法, 对所研究区域的高光谱数据波段选取至少10%的样本, 按照等差选取的原则选择出band4、 band12、 band20、 band28四个波段的显著图, 选取的样本覆盖了划分的三个子空间, 具有很强的代表性。 接下来检验四种显著性算法的检测效果, 实验中采用人工精细标注结果作为地面真值图, 流程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 显著性算法选择流程Fig.2 Selection process of saliency algorithm

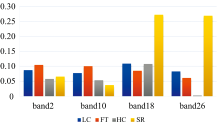
利用上述方法计算个显著性算法在样本中的值, 绘制为图3所示的柱状图。 SR算法虽然在band2和band10中的检测效果较好, 但由于在band18和band26中仅能检测到地物的边缘, 与地面真值产生较大误差, 可优先排除该算法。 FT算法在各个子空间都保持了较强的稳定性, 但相较于HC、 LC算法, 其平均绝对误差较大, 故可排除该算法。 对于HC和LC算法, 二者在原理上有很多类似之处, 其检测效果从图中分析同样具有很强的一致性, 结合二者在检验样本中的MAE的均值, 最终选取误差较小的HC算法。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同算法MAE值比较Fig.3 Comparison of MAE values for different algorithms

2.1.3 构建显著性波段选择模型

对于高光谱图像I_{w× h× l}, 它可以被看作一系列二维图像的集合{i₁, i₂, …, i_k}, i_k是图像I的第k波段。 利用HC显著性算法分别输出每个波段图像i_k的显著图S₍i_k), 根据地物目标显著性评价指标对所有地物C中两两不同的地物c和地物d进行对比度差异分析, 定义波段i_k的显著性为O Sik

OSik=∑c∈C, d∈C|S(ick)-S(idk)|(2)

图4和图5分别展示了研究区域中大小为360× 360像素的原始band3、 band16及其对应的HC显著图, 其中地物有建筑、 林地、 水体, 经过对比度的差异分析, band16的显著性O Sik更高, 在波段选择时应当优先考虑。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 band3裁剪区及对应HC显著图Fig.4 Band3 crop region and corresponding HC saliency map

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 band16裁剪区及对应HC显著图Fig.5 Band16 crop region and corresponding HC saliency map

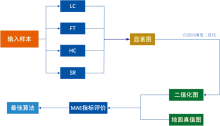
由于高光谱数据存在大量冗余信息, 为了更加有效地提取其中主要的光谱特征, 将高光谱数据划分为若干不相关的子空间是目前高光谱数据降维的主流方法。 唐厂^[14]等提出了一种基于近邻子空间划分的波段选择方法(band selection method via adjacent subspace partition, SEASP), 根本思想是设计的近邻子空间划分方法(adjacent subspace partition, ASP)。 根据高光谱图像波段相关系数具有分块的特性, 两个相邻子空间存在间断点, 在间断点处两相邻波段相关性底, 可以将此作为划分的依据。 下面设计一种改进近邻子空间划分(improved adjacent subspace partition, IASP)的方法, 该方法流程示意图如图6所示。 该方法主要思想为基于对珠海一号高光谱卫星数据的分析, 在近邻子空间划分基础上做出的改进。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 改进近邻子空间划分流程示意图Fig.6 Schematic diagram of improved neighbor subspace partitioning process

计算数据所包含波段两两之间的相关系数, GW_i与W_j两波段的相关系数r_{i, j}G计算原理如式(2)。

ri, j=∑k=1n(Wik-W̅i)(Wjk-W̅j)∑k=1n(Wik-W̅i)2∑k=1n(Wjk-W̅j)2(3)

式(3)中, W_ik和W_jk代表所在波段的第k个像素值, W̅i与 W̅j表示所在波段的均值, n表示图像中像素总数。 相关系数r_{i, j}越接近1, 表示相关性越强, 反之越弱。 结合图7数据源1分析, 曲线①和②分别为band26、 band2与其他波段的相关系数变化曲线, 曲线③为相邻波段相关系数变化曲线, 分割点处band18邻域相信波段相关系数值均较小, 即band17、band18、 band19与相邻波段之间相关系数较小, 均值为0.846 4, 而band1— band16之间相关系数均值为0.970 9, band20— band32之间相关系数均值为0.991 7; 在band17— band19之间, 各独立波段与其他波段之间的相关系数均产生急剧上升或下降。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 子空间划分结果(a): 数据源1; (b): 数据源2Fig.7 Subspace division results(a): Data source 1; (b): Data source 2

根据这一特性, 可将数据源1划分为三个互斥子空间: 1~16、 17~19、 20~32。 结果如图7(a)所示。

同样的, 可以将数据源2划分为三个互斥的子空间: 1~17、 18~21、 22~32, 1~16、 17~20、 21~32, 如图7(b)所示。

通过对比分析, 发现2个数据源的分割点均为band18, 只是在划分子空间的结果上存在1~2个波段的偏移。

在划分好的子空间中, 第Ⅰ 和第Ⅲ 子空间波段数目均达到10~15个, 并且在这一区间曲线变化平缓, 这表明第Ⅰ 和第Ⅲ 子空间内波段间的相关性很高, 存在较高的信息冗余现象, 在波段组合研究中, 要分别从这两个子空间内适当选取合理波段, 以避免合成的彩色影像出现信息缺失。 而第Ⅱ 子空间内波段数目仅有3~4个, 但波段相关系数却出现急剧变化, 这可能预示着这一区间的波段存在较多的地物空间分布信息, 因此在选取波段时, 还应当考虑从第Ⅱ 子空间内选择合理波段。

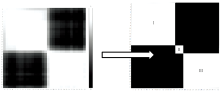
图8为计算高光谱数据相关性矩阵并可视化的结果, 相关系数越高, 灰度值越大。 其矩阵灰度图具有成块的特点, 根据这一特性可将高光谱数据空间划分为合适的子空间。 根据上述改进近邻子空间划分的方法, 结合单独波段相关系数及相邻波段相关系数曲线变化率, 设置阈值对可视化矩阵图进行二值化处理, 最终得到图8的矩阵图, 得到三个互斥的子空间, 二者结果高度相符。 这进一步印证了该方法的可行性。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 灰度矩阵及二值化Fig.8 Gray matrix and binarization

2.3.1 显著性波段选择结果

在前面划分的高光谱图像子空间内, 根据HC显著性对各个子空间内的波段进行排序, 选择出3个波段组合为波段子集。 经过划分的高光谱图像, 各个子空间内波段数目并不相同, 第Ⅱ 子空间内尽管波段数目较少, 但子空间内各个波段之间的相关系数均比较小, 第Ⅰ 子空间和第Ⅲ 子空间波段数目大致相同, 均衡二者的权重, 最终确定在三个子空间内分别选取2个波段组成波段子集。

各个子空间内进行波段显著性排序后, 如果选取排名前两名的波段, 会存在波段序号过近的现象, 考虑到波段之间的重叠和冗余, 这种选择方法增加了重复信息, 对波段组合研究意义不大。

为解决波段之间的冗余产生的困扰, 利用结构相似性SSIM滤除相似波段。 SSIM(structural similarity metric), 它基于人眼对图像结构信息敏感的特性, 用于评估两幅图像的相似度。 计算公式如式(4)和式(5)

SSIM(ix, iy)=(2uxuy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2)(4)

C1=(K1L)2, C2=(K2L)2(5)

式(4)和式(5)中, i_x和i_y是输入的两幅图像, u_x和u_y分别表示这两幅图像的均值, σx2和 σy2分别表示这两幅图像的方差, σ _xy表示这两幅图像的协方差。 C₁和C₂是常数, 用于避免分母为0的情况, L是像素值的范围。 K₁和K₂为适用于大多数图像处理任务一般基于经验选择取值为0.01和0.03, 能够有效平衡亮度和对比度的影响, 同时保持对结构相似性的敏感性。

SSIM的取值范围在-1到1之间, 其绝对值越接近于1, 则两个波段图像越相似; 越接近0, 则2个波段图像更不相关。 图9证明了SSIM作为滤除相似性波段的有效性。 计算各个子空间内各波段与最显著波段的SSIM, 若其高于所设定的阈值, 则排除该波段, 选择满足要求的波段。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 band30 (a)、 band31 (b)、 band10 (c) SSIM对比(1): band31和band30 SSIM=0.994 4; (2): band31和band10 SSIM=-0.069 7Fig.9 SSIM comparison of band30 (a), band31 (b), and band10 (c)(1): band31 and band30 SSIM=0.994 4; (2): band31 and band10 SSIM=-0.069 7

2.3.2 其他方法波段选择结果

为了避免实验重复性, 同时验证本波段选择方法的优势和有效性。 设计以下对比实验:

(1)基于交叉信息量的波段选择(MI);

(2)基于自适应波段选择在近邻子空间的波段选择(ABS_ASP)实验, 验证近邻子空间划分的合理性;

(3)基于最大信息量在改进近邻子空间的波段选择(MI_IASP)实验, 验证改进近邻子空间的合理性;

(4)基于HC显著性算法的波段选择(HC)。

各方法选择结果如表3所示。

表3

Table 3

表3(Table 3)

表3 波段选择结果 Table 3 Band selection results 数据源 方法 结果 数据源1 MI 26、 27、 28、 29、 30、 31 ABS_ASP 14、 15、 16、 28、 29、 31 MI_IASP 14、 15、 18、 19、 28、 29 HC 8、 16、 17、 19、 24、 31 数据源2 MI 22、 23、 27、 28、 30、 31 ABS_ASP 16、 17、 18、 21、 22、 23 MI_IASP 15、 16、 19、 21、 22、 23 HC 7、 14、 19、 21、 23、 28

表3 波段选择结果 Table 3 Band selection results

2.4.1 波段结果相关性

各个实验选择的波段组成为一个波段子集, 分别计算四个子集中六个波段间的相关系数之和。 相关系数之和越小, 波段选择效果越好^[15]。 如图10所示, HC显著性算法波段选择的子集表现出良好的性能。

图10

Fig.10

	Figure Option ViewDownloadNew Window
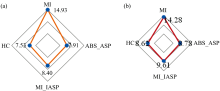	图10 各数据源波段子集相关系数之和(a): 数据源1; (b): 数据源2Fig.10 Sum of correlation coefficients for subsets of data source bands(a): Data source 1; (b): Data source 2

例如在数据源1中的band17, 地物的光谱反射值比较分散, 差异性显著; 在数据源2中的第二子空间中, 引入的显著性算法所选择的波段为band19、 band21, 通过对比该波段处的光谱反射值, 各类地物反射值差异性较大, 并且曲线出现陡峭变化, 说明在这2个波段处光谱反射变化率大, 数值变化明显。 其他方法选择的波段子集由于波段间过于相近, 各类地物的光谱变化趋势相近, 很难表现地物的可分性。

利用本方法选择的波段子集, 在各个数据源的三个子空间内光谱可分性较好, 最大程度上避免了光谱反射值相同的情况。

2.4.2 地物分类实验

将四种方法选取的波段子集分别进行地物分类实验, 采取支持向量机(SVM)监督分类、 最大似然(MLC)监督分类。

二者都属于监督分类方法, 首先要确定地物类别数目, 再创建训练样本, 同时保证样本中各类别间具有高可分离性, 最后执行监督分类。 前者的主要思想是建立一个最优决策超平面, 使该平面两侧距平面最近的两类样本之间距离最大化, 对分类问题提供良好的泛化能力; 后者的主要思想是假设每个类别在训练样本上服从特定的正太分布, 用统计方法根据最大似然比贝叶斯判决准则法建立非线性判别函数集, 计算各待分类样区的归属概率。 各数据源分类结果如图12 和图13所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 各数据源光谱曲线(a): 数据源1; (b): 数据源2Fig.11 Spectral curves of various data sources(a): Data source 1; (b): Data source 2

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 数据源1 SVM分类(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HCFig.12 Data source 1 SVM classification(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HC

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 数据源1MLC分类(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HCFig.13 Data source 1 MLC classification(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HC

根据图14和图15, 基于MI波段选择结果在SVM分类器中检测不到草地, 在MLC分类器中林地错分为草地的现象比较明显。 通过与卫星地面影像图对比, 发现HC算法波段选择的分类结果与真实地物一致。 如图14和图15, 数据源2中乡间小路上种植树林, 因此应被分为林地, 通过对比, 仅有本方法能够准确提取出来。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 数据源2 SVM分类(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HCFig.14 SVM classification of data source 1(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HC

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 数据源2 MLC分类(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HCFig.15 MLC classification of data source 2(a): MI; (b): ABS_ASP; (c): MI_IASP; (d): HC

通过对比各数据地物分类后的结果, 发现本方法在主观视觉上具有较好的效果。 各组数据经过基于MI的波段选择后进行分类得到的结果图中, 无论是SVM分类, 还是MLC分类, 均存在较大面积的错分、 漏分现象。

经过本文所提出的方法得出的波段子集, 在SVM和MLC分类后都比其他方法视觉效果好。 本方法得出的分类结果图不仅错分、 漏分情况少, 而且边界都比较清晰明显, 同类地物均聚集成簇, 有利于各类信息的提取。

2.4.3 分类精度评价

计算分类后的混淆矩阵, 选取矩阵中的总体精度(overall accuracy, OA)、 Kappa系数进行综合评价。 总体分类精度是指被正确分类的样本总数占总体样本个数的比例, 如式(6)。

OA=∑i=1npii∑j=1n∑i=1npij(6)

Kappa系数衡量分析结果图和真实所标注图形之间重合程度的指数。 其计算公式如式(7)所示。

Kappa=M* TP-∑m=1M(Cm+C+m)M2-∑m=1M(Cm+C+m)(7)

式(7)中, Cm+=∑i=1MCmi是行元素之和, C+m=∑i=1MCim是列元素之和(m=1, 2, 3, …, M)。

根据表4分析, 四种波段选择结果中, HC算法波段选择进行图像分类具有稳定优异的表现。 数据源1分类后的精度中, 本方法SVM和MLC分类精度相近, 总体精度分别为95.125 8%和95.243 7%, 分别比MI波段选择结果提高9.984 3%、 11.556 6%; Kappa系数分别为0.934 9和0.937 3, 分别比MI波段选择结果提高0.135 6、 0.151 1。 相对于本文设计的对比实验(ABS_ASP、 MI_IASP), 两种分类方法的总体精度和Kappa系数分别提高0.5%~2%、 0.1~0.2不等。 数据源2的分类精度与数据源1有相似性, 总体结果表明本文提出的波段选择结果效果最佳。

表4

Table 4

表4(Table 4)

表4 OA和Kappa系数 Table 4 OA and Kappa coefficients 数据源 波段选择 方法 SVM MLC OA Kappa OA Kappa 数据源1 MI 85.141 5% 0.799 3 83.687 1% 0.786 2 ABS_ASP 94.378 9% 0.925 0 93.317 6% 0.912 2 MI_IASP 94.182 4% 0.922 3 93.199 7% 0.910 6 HC 95.125 8% 0.934 9 95.243 7% 0.937 3 数据源2 MI 78.642 3% 0.705 2 67.092 6% 0.580 7 ABS_ASP 93.440 1% 0.912 2 90.328 6% 0.873 4 MI_IASP 93.265 3% 0.909 8 89.616 7% 0.863 6 HC 93.881 9% 0.918 1 90.649 6% 0.877 1

表4 OA和Kappa系数 Table 4 OA and Kappa coefficients

在各个数据源中, 本文方法的OA和Kappa系数都是最高的。 这进一步说明该波段子集所包含的地物的光谱信息、 空间分布信息都是最佳的, 为下一步波段组合研究奠定良好基础。