基于双TV4正则化的能谱CT投影域材料分解方法研究

引用本文

于鑫丽, 孔慧华, 张然. 基于双TV4正则化的能谱CT投影域材料分解方法研究[J]. 光谱学与光谱分析, 2025,45(10): 2935-2941.
YU Xin-li, KONG Hui-hua, ZHANG Ran. A Study of Double TV4 Regularization Based Spectral CT Projection Domain Material Decomposition Method[J]. Spectroscopy and Spectral Analysis, 2025,45(10): 2935-2941.
Doi:10.3964/j.issn.1000-0593(2025)10-2935-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于双TV4正则化的能谱CT投影域材料分解方法研究

于鑫丽^1,², 孔慧华^1,^2,^*, 张然^1,²

1. 中北大学数学学院, 山西太原 030051

2. 极限环境光电动态测试技术与仪器全国重点实验室, 山西太原 030051

*通讯作者 e-mail: huihuak@163.com

作者简介: 于鑫丽, 女, 2000年生, 中北大学数学学院硕士研究生 e-mail: 1678230834@qq.com

收稿日期: 2025-04-03 修回日期: 2025-07-16

基金: 国家重点研发计划项目(2023YFE0205800), 国家自然科学基金联合基金项目(U23A20285), 山西省重点研发项目(202302150401011), 山西省基础研究计划项目(202403021223006), 山西省科技成果转化引导专项(202304021301028), 山西省留学基金项目(2023-129)资助

摘要

能谱CT可以利用不同X射线能量下材料衰减特性的差异, 区分不同的材料成分。基于投影的材料分解是一种常用的材料分解方法, 分为投影域分解和基材料图像重建两个步骤。针对该方法在分解过程中容易受到噪声污染的问题, 提出一种基于双正则化的两步分解方法, 将四方向总变分(TV4)正则化先验同时引入到材料分解和基图像重建中。 TV4在传统总变分(TV)基础上扩展至四个方向梯度, 能够更全面地捕捉材料图像中的多方向边缘, 联合优化抑制噪声, 在低剂量或高噪声数据中更具鲁棒性。实验采用仿真模体与临床前真实小鼠的多个能量通道投影数据进行实验, 验证提出算法的有效性。在投影分解步骤, 对比分析提出的TV4算法与LS算法、 SR-TF算法在分解上的去噪结果。为进一步验证所提方法在材料分解精度上的性能, 对比分析不同步骤上的正则化方法与本文提出的双正则化策略获得的基材料图像, 并采用均方根误差(RMSE)和峰值信噪比(PSNR)指标对分解结果定量分析。实验结果表明, 本文提出的算法能够清晰地分解出不同基材料的图像, 对应PSNR值是所有方法中最高的且具有最小的RMSE值, 说明本算法有效抑制了分解中噪声和伪影的干扰, 提高了基材料图像的质量。

关键词: 能谱CT; 双TV4正则化; 材料分解; 投影分解; 基图像重建

中图分类号:TP391 文献标志码:A

A Study of Double TV4 Regularization Based Spectral CT Projection Domain Material Decomposition Method

YU Xin-li^1,², KONG Hui-hua^1,^2,^*, ZHANG Ran^1,²

1. School of Mathematics, North University of China, Taiyuan 030051, China

2. National Key Laboratory of Photoelectric Dynamic Testing Technology and Instrument for Extreme Environments, Taiyuan 030051, China

*Corresponding author

Abstract

Spectral computed tomography (CT) can distinguish different material compositions by utilizing the differences in material attenuation characteristics under various X-ray energies. Projection-based material decomposition is a commonly used method, which consists of two steps: projection-domain decomposition and basis-material image reconstruction. To address the susceptibility of this method to noise contamination during decomposition, this study proposes a double-regularized two-step decomposition framework that simultaneously incorporates four-directional total variation (TV4) regularization priors into both material decomposition and basis image reconstruction. Extending conventional total variation (TV) to four-directional gradients, TV4 demonstrates enhanced capability in comprehensively capturing multi-directional edges within material images while achieving joint optimization for noise suppression, thereby exhibiting superior robustness in low-dose or high-noise scenarios. Experimental validation was conducted using multi-energy channel projection data from both simulated phantoms and preclinical in vivo mice. In the projection decomposition phase, the proposed TV4 algorithm was compared with conventional LS and SR-TF algorithms in terms of denoising performance. To further evaluate the material decomposition accuracy, basis material images obtained through different regularization strategies were quantitatively compared using root mean square error (RMSE) and peak signal-to-noise ratio (PSNR) metrics. Results demonstrate that the proposed algorithm achieves a clear separation of basis material images, attaining the highest PSNR values and the lowest RMSE values among all compared methods. These findings confirm the method’s effectiveness in suppressing noise and artifact interference during decomposition while significantly enhancing basis material image quality.

Keyword: Spectral CT; Double-TV4 regularization; Material decomposition; Projection decomposition; Base image reconstruction

文章图片

引言

基于光子计数探测器^[1](photon counting detector, PCD)的能谱CT系统可以获取不同能量区间的投影数据, 有助于区分物质成分, 确定成像物体内的组织分布^[2]。理论上能谱CT系统获取的投影数据信噪比(SNR)低于传统CT。受X射线荧光、电荷共享、 K逃逸和脉冲堆积等因素影响, 投影数据会受到未知噪声的干扰^[3], 进而影响材料分解的准确性。

为了提高分解的准确性, 需要考虑物理效应和更多正则化先验, 研究先进的材料分解方法。一般来说, 分解方法可划分为对投影域分解和对图像域分解这两类^[4]。本文主要针对投影域分解方法进行研究, 基于投影域的方法在实现时可分为各能量通道的投影数据被分解为基材料正弦图和使用重建技术得到最终的基材料图像这两个步骤^[5]。这种方法能有效抑制分解过程中射束硬化效应引发的伪影同时, 允许并行计算实现每个投影数据集的分布式独立分解, 从而显著提升分解过程的运算效能。因此, 科研工作者开发了诸多基于投影域的材料分解算法。孙英博等^[6]基于基效应模型, 利用最小二乘算法(least squares, LS)在能谱CT的投影域中进行材料分解。 Ducros等^[7]提出了在投影域中对不同材料引入特定的正则项(specific regularization, SR)的投影分解算法, 分解问题使用Gauss-Newton算法迭代求解, 该算法可以从快速线性求解器中受益。 Cong等^[8]提出了基于单变量优化的双能CT投影分解方法, 该方法结合了多项式方程的解析解和单变量优化来求解多色非线性积分方程, 对双能CT图像进行准确稳定的分解。

在投影域分解中, 其不足是分解过程会不可避免地引发噪声水平放大, 导致信噪比降低的影响。为解决这一问题, 人们也提出了许多分解算法与有效的去噪方法相结合的策略。 Tang等^[9]提出了基于投影域多尺度分解和惩罚加权最小二乘法进行统计CT降噪的算法。 Lu等^[10]提出了一种基于低秩和基于相似性正则化(LRSBR)的去噪算法。该算法将张量的低秩特征整合到基于相似性的正则化(SBR)框架中, 有效解决了SBR算法中边缘像素不稳定的问题, 增强了双能图像的结构一致性, 有效地抑制双能CT材料分解的噪声。李佳欣等^[11]在SR的基础上应用张量分解, 提出了基于特定材料和张量分解正则项(SR-TF)的投影分解算法, 并有效抑制了分解噪声。 Wu等^[12]提出了基于两步正则化的材料分解算法, 在重建和分解后处理步骤中引入总变分最小化(TVM)作为实现的正则化, 同时抑制了重建和分解两方面的噪声。 TVM是一种常用的约束方法, 用于增强每个能量通道下能谱CT图像的稀疏性, 提高了分解准确性。

在材料分解模型与图像重建模型框架中协同融入正则化先验约束, 这相较于只在分解中引入正则化的方案, 能进一步提高材料分解的精度。因此, 本文基于文献[12]提出的图像域重建和材料分解两步正则化方法的思想。为了抑制在投影域分解和图像重建两步骤中产生的噪声和伪影并提高图像质量, 在该两步过程中同时引入四方向总变分(four-directional total variation, TV4)正则化先验, 提出了一种基于双TV4(double-TV4, D-TV4)正则化的投影域材料分解算法。首先在投影分解步骤引入TV4将多个能量通道获得的投影数据分解为各基材料的投影图, 然后在各基材料图像重建步骤利用SART算法结合TV4对基材料投影进行重建, 得到每种物质的分解图像。此外, 通过实验进行定性与定量比较分析在不同步骤上的正则化优势, 说明D-TV4正则化策略对于提高材料分解的性能。

1 理论与方法

1.1 投影分解

依据Lambert-Beer定律, X射线穿过物体时的衰减特性由物体自身的物理化学属性决定。对于由多种材料组成的非均质物体, 不同材料的衰减系数存在特征性差异^[13]。基于光子计数探测器(PCD)捕获的光子数可表示为

$I (E) = \int_{E} I_{0} (E) S (E) e^{- \int_{L} μ (E, r) d r} d E$ (1)

式(1)中, I₀为入射光子数量, I为探测器接收到的光子数, S(E)为光子的等效能谱强度, μ (E, r)为物体材料的总线性衰减系数, L表示射线穿过物体的路径。

沿路径L的投影P则可以表示为

$P = \ln \frac{I_{0}}{I} = \ln (\frac{I_{0} (E)}{\int_{E} I_{0} (E) S (E) e^{- \int_{L} μ (E, r) d r} d E})$ (2)

根据材料分解理论, 物体的总线性衰减系数μ (E, r)可由N种基材料的衰减系数的线性组合表示

$\begin{array}{l} μ (E, r) = f_{1} (E) a_{1} (r) + \dots + f_{N} (E) a_{N} (r) \\ = \overset{N}{\sum_{n = 1}} f_{n} (E) a_{n} (r) \end{array}$ (3)

式(3)中, f_n(E)和a_n(r)分别表示第n种基材料的衰减函数和质量密度。

将式(3)代入到式(2)中整理得

$P = \overset{N}{\sum_{n = 1}} \int_{L} f_{n} (E) a_{n} (r) d r = \overset{N}{\sum_{n = 1}} f_{n} (E) A_{n} (r)$ (4)

式(4)中, $A_{n} (r) = \int_{L} a_{n} (r) d r 表示分解后 N$ 种基材料的投影。

因此, 在M个能量通道下的投影P_m(m=1, 2, …, M)与分解后的N种基材料投影A_n(n=1, 2, …, N)之间的关系可以用矩阵的形式表示为

$P = FA$ (5)

其中,

$\begin{array}{l} P = [P_{1} P_{2} \dots P_{M}]^{T} \\ F = [\begin{array}{l} f_{1} (E_{bin 1}) & f_{2} (E_{bin 1}) & \dots & f_{N} (E_{bin 1}) \\ f_{1} (E_{bin 2}) & f_{2} (E_{bin 2}) & \dots & f_{N} (E_{bin 2}) \\ ⋱ \\ f_{1} (E_{bin M}) & f_{2} (E_{bin M}) & \dots & f_{N} (E_{bin M}) \end{array}] \\ A = [A_{1} A_{2} \dots A_{N}]^{T} \end{array}$ (6)

1.2 基于TV4正则项的投影域材料分解

材料的衰减系数与X射线能谱之间的关系是非线性的, 并且材料的分解过程是不稳定的。然而, 最小二乘算法(LS)直接反演求解方程组的投影分解问题中, 该算法并未考虑多个能量通道的分解中投影数据会受到泊松噪声的影响, 可能会导致分解结果不准确。因此, 根据Ducros等^[7]提出的基于特定材料正则项的投影分解算法, 将分解问题表述为最小化问题求解

$\min_{A} ‖ P - FA ‖_{2}^{2}$ (7)

由于TV4考虑四个方向的梯度信息, 能够更好地捕捉不同方向的结构信息。在多方向上施加稀疏性约束, 可以有效地去除噪声和减少单一方向引起的伪影, 同时保留更多细节特征和复杂纹理^[14]。为了抑制分解中噪声的影响, 本文提出在方程式(7)中引入TV4的正则化先验约束, 构成目标函数如式(8)

$\arg \min_{A} \frac{α}{2} ‖ P - FA ‖_{2}^{2} + λ R_{TV 4} (A)$ (8)

式(8)中, $\frac{1}{2}$ ‖ P-FA $‖_{2}^{2}$ 为数据保真项, α 为保真项的参数, λ 为正则项的参数, 正则项函数R_TV4(A)如式(9)所示

$R_{TV 4} (A) = ‖ D_{0} A ‖_{1} + ‖ D_{90} A ‖_{1} + ‖ D_{45} A ‖_{1} + ‖ D_{135} A ‖_{1}$ (9)

式(9)中, D_θ表示在0° 、 90° 、 45° 和135° 四个方向上的差分算子, ‖ · ‖ ₁表示矩阵的L₁范数。

为实现目标函数式(8)的优化, 引入辅助变量Z替代原变量A, 得到

$\begin{array}{l} \arg \min_{A, Z} \frac{α}{2} ‖ P - FA ‖_{2}^{2} + λ R_{TV 4} (Z) \\ s.t. Z = A \end{array}$ (10)

将惩罚项 $\frac{η}{2}$ ‖ A-Z $‖_{2}^{2}$ 加入式(10)中, 构成无约束优化形式, 如式(11)所示

$\arg \min_{A, Z} \frac{α}{2} ‖P - FA ‖_{2}^{2} + λ R_{TV 4} (Z) + \frac{η}{2}‖ A - Z ‖_{2}^{2}$ (11)

对式(11)转化为以下两个子问题, 进行交替迭代优化更新

$\arg \min_{A} \frac{α}{2} ‖P - FA ‖_{2}^{2} + \frac{η}{2}‖ A - Z ‖_{2}^{2}$ (12)

$\min_{Z} \frac{η}{2} ‖ A - Z ‖_{2}^{2} + λ R_{TV 4} (Z)$ (13)

针对式(12)所描述的非线性问题, 采用高斯-牛顿(Gauss-Newton, GN)算法迭代求解A₍_k₊₁₎, 即

$A_{(k + 1)} = A_{(k)} + φ_{(k)} δ A_{(k)}$ (14)

式(14)中, φ ₍_k₎为迭代步长, δ A₍_k₎∈ R^M^×^N为GN步长, 可由式(15)— 式(18)求解。

$H_{k} = α ((F A_{(k)})'^{T} {(F A_{(k)})}^{'}) + ηI$ (15)

$g_{k} = α ((F A_{(k)})'^{T} (P - F A_{(k)})) + φ (A_{(k)} - Z)$ (16)

其中, H_k和g_k分别为式(12)的Hessian矩阵和梯度。

$δ A_{(k)} = - (H_{k})^{- 1} g_{k}$ (17)

借助在GN方向上提供的方向最小化成本函数, 确定迭代步长φ ₍_k₎, 其形式为

$φ_{(k)} = \arg \min_{φ} L (A_{(k)} + φδ A_{(k)})$ (18)

针对式(13)的子问题采用梯度下降法求解, 计算梯度

$\nabla_{Z} (\frac{η}{2} ‖ A - Z ‖_{2}^{2}) = η (Z - A)$ (19)

$\nabla_{Z} R_{TV 4} (Z) = G_{0} + G_{90} + G_{45} + G_{135}$ (20)

其中, G_θ_{∈ {0° , 90° , 45° , 135° }}表示在每个方向上的梯度贡献, 具体形式如式(21)所示

$G_{θ} (i, j) = \{\begin{array}{l} - sign (D_{θ} Z (i, j)) \\ + sign (D_{θ} Z (i, j)) \end{array}$ (21)

将式(19)与式(20)两部分的梯度结合, 得到总梯度

$\nabla_{total} = η (Z_{(k)} - A_{(k)}) + λ (G_{0} + G_{90} + G_{45} + G_{135})$ (22)

迭代k₁次更新辅助变量Z

$Z_{(k + 1)} = Z_{(k)} - β \nabla_{total}$ (23)

式(23)中, β 表示梯度下降的步长。

1.3 基于TV4正则项的基材料投影重建

受X射线辐射剂量^[15]、扫描范围^[16]、系统噪声^[17]等因素的限制, 对分解后的基材料投影重建时, 也会产生不必要的噪声和条纹伪影干扰, 影响基材料重建图像的质量和细节清晰度。在上述中, 由于TV4具有有效抑制噪声和伪影的效果, 将其并行应用于重建过程中达到更好的分解结果。

根据CT图像重建数学模型可知, 分解得到的第n种基材料投影A_n(n=1, 2, …, N)的重建可以被表征为线性规划问题迭代求解

$\min_{u_{n}} \frac{1}{2} ‖ B u_{n} - A_{n} ‖_{2}^{2}$ (24)

式(24)中, A_n∈ $R^{J_{1} \times J_{2}}$ 表示第n种基材料投影数据, J₁和J₂分别表示扫描的投影角度数和探测器单元数, u_n∈ $R^{I_{1} \times I_{2}}$ 表示第n种基材料的目标重建图像, I₁和I₂分别表示重建图像的高和宽, B∈ $R^{(I_{1} \times I_{2}) \times (J_{1} \times J_{2})}$ 表示CT扫描结构中的系统矩阵。

引入TV4正则化约束的基材料图像重建算法的数学模型表示为

$\min_{u_{n}} \frac{1}{2} ‖ B u_{n} - A_{n} ‖_{2}^{2} + \frac{γ}{2} R_{TV 4} (u_{n})$ (25)

式(25)中, 第一项为数据保真项, 通过计算最小化目标图像u_n与基材料投影A_n之间的误差实现。第二项是正则化项, 由参数γ 调控, 用于平衡数据拟合与先验约束。

对于式(25), 采用交替迭代法进行求解。保真项的求解采用SART算法, 正则化项的求解采用上述的梯度下降法。

整个算法步骤如表1所示。

表1 D-TV4算法步骤伪代码 Table 1 The pseudocodes of D-TV4 algorithm steps

分解步骤:
输入: 多能量通道投影数据P, 衰减系数矩阵F, 迭代次数K, 参数α , λ , η , k₁, β , 初始化变量A₍₀₎和Z₍₀₎ 主程序迭代: 当k< K时, 执行迭代: 利用式(14)— 式(18)高斯牛顿法求解更新A₍_k₊₁₎; 利用式(19)— 式(23)梯度下降法求解更新Z₍_k₊₁₎; k=k+1; 直到k=K, 停止迭代, 输出基材料投影A。
重建步骤:
输入: 第n种基材料投影A_n, 系统矩阵B, 迭代次数K₂, 参数γ , β , 初始化变量u_n₍₀₎ 主程序迭代: 当k₂< K₂时, 执行迭代: SART算法迭代更新式(25)的 $u_{n (k_{2} + 1)}^{temp}$ ; 梯度下降法对 $u_{n (k_{2} + 1)}^{temp}$ 更新优化得到 $u_{n (k_{2} + 1)}$ ; k₂=k₂+1; 直到k₂=K₂, 停止迭代, 输出基材料重建图像u_n。

表1 D-TV4算法步骤伪代码 Table 1 The pseudocodes of D-TV4 algorithm steps

2 实验与结果讨论

为验证本文提出的投影域材料分解模型和基材料图像重建模型耦合相同正则化的材料分解准确性, 本研究构建了数字模体仿真模型、小鼠胸腔仿真模型及临床前真实小鼠数据作为实验验证体系。在投影分解模型对比实验中, 采用LS算法^[6]、 SR-TF算法^[11]作为对比算法; 在基材料重建模型对比实验中, 选取直接投影分解(projection decomposition, PD)后材料重建(material reconstruction, MR)(PD-MR)、 TV4分解后重建(TV4-MR)、分解后TV4重建(PD-TV4)作为对比方法, 与本文提出的双TV4(D-TV4)结果比较。针对材料分解性能的定量评估, 采用基于像素域差异的均方根误差(RMSE)及反映空间分辨特性的峰值信噪比(PSNR)作为双指标评价体系, 通过计算重建图像的边缘保持度与噪声抑制水平, 实现算法性能的量化分析。

2.1 模体仿真实验

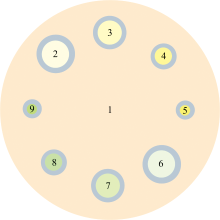
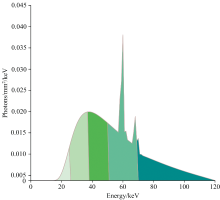
实验设计仿真模体包含软组织、骨骼、碘和钆四种材料, 其中背景区域的大圆代表软组织, 标号为2、 3、 4、 5的小圆分别为0.2%、 0.4%、 0.6%、 0.8%浓度的碘造影剂, 6、 7、 8、 9的小圆分别为0.1%、 0.2%、 0.3%、 0.4%浓度的钆造影剂, 小圆外围的灰色圆圈部分为不同厚度的骨物质。仿真模体图如图1所示, 模体大小为10mm× 10mm, 分辨率为256× 256。本实验运用SpekCalc软件来模拟管电压为120 kVp时的源能谱, 设定X射线源到旋转中心的距离为100 mm, 探测器的长度为20 mm, 且探测器单元数为320个, 单次扫描在[0, 2π )范围内均匀采集360个角度的投影数据。 120 kVp下的归一化能谱如图2所示, 依据四种材料的K-edge值及能量衰减特性, 将此宽能谱划分为4个能量通道进行模体仿真实验, 分别为: [16, 28]、 [30, 41]、 [50, 80]和[80, 120] keV。

	Figure Option View Download New Window
	图1 仿真模体横截面图Fig.1 Cross-sectional image of a simulated phantom

	Figure Option View Download New Window
	图2 120 kVp下的归一化能谱图Fig.2 Normalized energy spectrum at 120 kVp

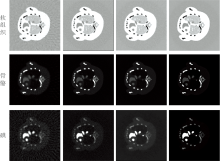
本文经过多次实验调整, 将分解的参数设置为: α =1, 针对不同材料调整λ =[0.001 0.005 0.000 3 0.000 9], k₁=50, η =0.05, k=10。重建的参数设置为: γ =[0.06 0.06 0.04 0.04], k₂=30。在5× 10⁵光子数下, 利用LS算法、 SR-TF算法和本文所提出的TV4算法对模体进行投影域材料分解, 其分解投影图如图3所示。分解出的四种物质的投影图从上到下依次对应为软组织、骨骼、钆和碘, 从左到右依次为LS、 SR-TF和TV4算法的分解去噪结果。由图3分解结果可以看出LS、 SR-TF和TV4算法都可以将四种物质分解开。 SR-TF算法的分解结果比LS算法包含更小噪声, 而TV4算法分解的四种物质的噪声最小, 抑制噪声效果最明显, 尤其在骨骼分解投影图表现最为突出, 体现了本文提出的TV4算法在投影域分解方面去噪效果的有效性。

	Figure Option View Download New Window
	图3 LS、 SR-TF和TV4算法的投影分解图Fig.3 Projection decomposition images of LS, SR-TF, and TV4 algorithms

图4(a— d)是分别在不同步骤上加入正则化获得的四种基材料图像结果。从左到右依次为PD-MR方法、 TV4-MR方法、 PD-TV4方法作为对比方法和本文提出的D-TV4方法。从图4中可以看出, 在PD-MR结果中软组织和骨骼图像受到严重的噪声污染, 其细微结构和特征被噪声淹没; 钆和碘图像重建过程中还产生了条纹伪影的干扰, 且碘中存在少量骨物质的串扰, 分解准确性降低。与PD-MR方法相比, TV4-MR方法和PD-TV4方法能够提供更好的材料图像质量。在TV4-MR结果中, 分解中的噪声得到了部分抑制, 但在重建时图像特征周围伪影严重, 这是由于SART重建的图像引起伪影, 最终的分解结果受到影响。 PD-TV4结果中, 钆和碘图像的伪影被有效去除, 但分解步骤受到严重噪声的干扰, 骨骼图像的边缘结构未能准确分出。然而, D-TV4方法可以进一步提高材料成分的准确性, 四种物质的分解结果都得到很好的噪声伪影抑制效果且物质边缘细节结构清晰。由于D-TV4继承了PD-TV4和TV4-MR的优点, 它在材料分解和重建中可以进一步提高材料精度, 进而获得高质量的基材料图像。

	Figure Option View Download New Window
	图4 不同步骤加入正则化的基材料重建图像(a): PD-MR; (b): TV4-MR; (c): PD-TV4; (d): D-TV4Fig.4 Basis material reconstruction images with regularization incorporation at different steps(a): PD-MR; (b): TV4-MR; (c): PD-TV4; (d): D-TV4

为了定量分析D-TV4方法提高材料分解精度的性能, 利用PSNR计算其分解质量和RMSE计算其分解误差, 实验的量化结果如表2所示。对表2的数值比较可知, 相比于对比方法, D-TV4对于每种基材料总能实现最高PSNR和最小RMSE值。通过数值比较, 进一步证明了在分解和重建步骤的双正则化可以提高材料分解的精度。

表2 依据各基材料的量化评估结果 Table 2 Quantitative evaluation results for Basis materials

2.2 小鼠胸腔仿真实验

为进一步验证算法的有效性, 采用仿真小鼠胸腔的能谱CT数据作为测试数据, 分辨率为512× 512。在50 kVp管电压下的源能谱进行, 采用3个能量通道的投影数据作为输入, 能量范围选取为[20, 30)、 [30, 40)和[40, 50] keV。在小鼠胸腔切片的血液中加入浓度为1.2%的碘造影剂, 构建由软组织、骨骼和碘三种材料组成的仿真小鼠模体。实验将分解的参数设置为: α =1, 对三种材料参数选择λ =[0.004 0.000 5 0.000 05], k₁=50, η =0.03, k=10。重建的参数设置为: γ =[0.05 0.05 0.04], k₂=30。

在5× 10⁵光子数下进行小鼠胸腔仿真实验, 投影域分解步骤采用LS算法、 SR-TF算法作为比较算法, 对所提出算法的分解效能加以验证。投影分解结果如图5所示, 分解的基材料投影重建结果如图6所示。由图6(a— d)可知, 小鼠胸腔仿真实验的各方法结果与模体仿真实验类似。 PD-MR分解的图像受到强噪声和伪影的污染。 PD-TV4结果中软组织和碘图像存在更多的噪声干扰。 TV4-MR获得了较好的分解结果, 但对额外产生的伪影没有明显见效。而使用本文方法分解的图像, 具有更好的结果。尤其在碘造影剂方面, 可以看出碘图像在清晰度和边缘锐利度方面表现最优, 其噪声水平和伪影数量显著低于对比方法的结果。此外, 还消除了

	Figure Option View Download New Window
	图5 LS、 SR-TF和TV4算法的模拟小鼠胸腔投影分解图Fig.5 Projection decomposition images of a simulated mouse thorax using LS, SR-TF, and TV4 algorithms

	Figure Option View Download New Window
	图6 不同步骤加入正则化的模拟小鼠胸腔基材料重建图像(a): PD-MR; (b): TV4-MR; (c): PD-TV4; (d): D-TV4Fig.6 Basis material reconstruction images of a simulated mouse thorax with regularization incorporation at different steps(a): PD-MR; (b): TV4-MR; (c): PD-TV4; (d): D-TV4

前三种对比方法中残留的软组织结构。因此本文所提出的D-TV4 方法在投影域材料分解中可以获得高精度的碘图像。同样计算PSNR和RMSE来评估四种方法对模拟小鼠胸腔的分解性能, 结果如表3所示。由表3可知, 本文提出的D-TV4 方法的各基材料PSNR值更高且对应的RMSE值也最小, 图像质量更好。

表3 模拟小鼠胸腔的各基材料量化结果 Table 3 Quantitative evaluation results for Basis materials in a simulated mouse thorax

通过定性与定量的分析, 在投影域基材料分解上, 相较于PD-MR、 TV4-MR和PD-TV4算法, 本文提出的D-TV4算法在材料分解性能中表现更好, 不仅能实现清晰的材料分离与锐利的边缘保持, 还能减小受其他物质串扰的影响。在微小结构方面相对保留了一些细节特征, 有效抑制了噪声和伪影, 使图像更加清晰, 分解质量更高。

2.3 真实小鼠实验

为验证提出算法在临床前的适用性, 采用MARS微型CT获得的一组真实小鼠能谱CT投影数据用于算法的测试。实验系统配置为120 kVp/175 mA, X射线源距旋转中心为158 mm, 距探测器为255 mm。整个能谱范围内收集了13个通道的投影数据, 从中选取了4个通道的数据作为实验输入。处理后的投影图像分辨率为360× 512, 重建图像的分辨率为512× 512。与模拟仿真实验相同, 算法中的参数通过实验优化确定, 实验中分解参数为: α =1, λ =[0.2 0.09], k₁=30, η =0.03, k=10, 重建参数为: γ =[0.5 0.5], k₂=30。

图7展示了4种算法下分解的临床前真实小鼠基材料重建图像, 可以看出, 每个算法分解的效果与以上仿真实验分解的效果基本相同。前三种算法的分解结果都有较大噪声和伪影的干扰, 物质边缘结构模糊。而D-TV4算法分解的软组织图像结构更加明显, 且噪声和伪影更少。骨骼图像对比黄框中骨物质的边缘结构, 可以看出本文算法分解的骨更清晰, 细节更加突出。

	Figure Option View Download New Window
	图7 临床前真实小鼠分解图像(a): PD-MR; (b): TV4-MR; (c): PD-TV4; (d): D-TV4Fig.7 Decomposition images of a real mouse in preclinical studies(a): PD-MR; (b): TV4-MR; (c): PD-TV4; (d): D-TV4

3 结论

针对能谱CT投影域材料分解过程中噪声污染及伪影干扰等问题, 提出了一种基于双正则化(D-TV4)的两步分解算法。在投影域分解和基材料图像重建中同时引入TV4正则化先验, 克服了传统TV因方向局限性和阶梯效应对多材料分解的限制, 实现了对噪声和伪影的协同抑制, 显著提升了材料分解的精度与图像质量。实验结果表明, 本文所提出的双正则化策略相较于传统LS分解算法及SR-TF分解算法, 可以使图像的边缘特征更清晰, 噪声更少, 在仿真实验和真实小鼠实验中均表现出了优越性能。本文的研究方法为能谱CT投影域材料分解提供了一种高效的双正则化解决方案, 这对提高能谱CT材料分解精度具有重要意义。

本文提出的研究方法在低剂量或高噪声数据中表现出良好的鲁棒性, 然而, 在极低剂量数据下, 噪声水平更高的情况下, 该方法的性能仍待验证。因此, 在未来的研究工作中, 将针对在更低剂量的投影数据上进行实验, 以验证该方法在极端条件下的性能。同时, 将结合深度学习与低剂量重建模型, 构建适用于极低剂量场景的联合处理框架, 以进一步提高图像质量。

参考文献

文献列表

[1]	Ren L, Zheng B, Liu H. Journal of X-Ray Science and Technology, 2018, 26(1): 1. [本文引用:1]
[2]	Lee Y, Lee S, Kim H J. Nuclear Instruments & Methods in Physics Research Section A-Accelerators Spectrometers Detectors and Associated Equipment, 2016, 815: 68. [本文引用:1]
[3]	Taguchi K, Stierstorfer K, Polster C, et al. Medical Physics, 2018, 45(11): 4822. [本文引用:1]
[4]	Zhang T, Yu H, Xi Y, et al. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 4501313. [本文引用:1]
[5]	Bussod S, Abascal J F P J, Arridge S, et al. Convolutional Neural Network for Material Decomposition in Spectral CT Scans 28th European Signal Processing Conference (EUSIPCO 2020). IEEE, 2021: 1259. [本文引用:1]
[6]	SUN Ying-bo, KONG Hui-hua, ZHANG Yan-xia(孙英博, 孔慧华, 张雁霞, 等). Journal of North University of China(Natural Science Edition)[中北大学学报(自然科学版)], 2019, 40(2): 167. [本文引用:2]
[7]	Ducros N, Abascal J F P J, Sixou B, et al. Medical Physics, 2017, 44(9): E174. [本文引用:2]
[8]	Cong W, De Man B, Wang G. Journal of X-Ray Science and Technology, 2022, 30(4): 725. [本文引用:1]
[9]	Tang S, Tang X. Medical Physics, 2012, 39(9): 5498. [本文引用:1]
[10]	Lu C, Han Z, Zou J. Journal of X-Ray Science and Technology, 2024, 32(3): 549. [本文引用:1]
[11]	LI Jia-xin, KONG Hui-hua, QI Zi-wen, et al(李佳欣, 孔慧华, 齐子文, 等). Microcontrollers & Embedded Systems(单片机与嵌入式系统应用), 2023, 23(12): 44. [本文引用:2]
[12]	Wu W, Chen P, Vardhanabhuti V V, et al. IEEE Access, 2019, 7: 158770. [本文引用:2]
[13]	Holburg J, Figul S, Charvat A, et al. X-Ray Spectrometry, 2025. doi: DOI:10.1002/xrs.3474. [本文引用:1]
[14]	Zhou X, Fan M. IEEE Access, 2021, 9: 27601. [本文引用:1]
[15]	Zhang W, Huang B, Chen S, et al. IEEE Transactions on Computational Imaging, 2024, 10: 1763. [本文引用:1]
[16]	Sheng W, Zhao X, Li M. Physics in Medicine and Biology, 2020, 65(23): 235038. [本文引用:1]
[17]	Tang X, Ren Y, Xie H. Journal of Applied Clinical Medical Physics, 2023, 24(1). doi: DOI:10.1002/acm2.13830. [本文引用:1]

2018

0.0

... 引言基于光子计数探测器^[1](photon counting detector, PCD)的能谱CT系统可以获取不同能量区间的投影数据, 有助于区分物质成分, 确定成像物体内的组织分布^[2] ...

2016

0.0

2018

0.0

... 受X射线荧光、电荷共享、 K逃逸和脉冲堆积等因素影响, 投影数据会受到未知噪声的干扰^[3], 进而影响材料分解的准确性 ...

2023

0.0

... 一般来说, 分解方法可划分为对投影域分解和对图像域分解这两类^[4] ...

2021

0.0

... 本文主要针对投影域分解方法进行研究, 基于投影域的方法在实现时可分为各能量通道的投影数据被分解为基材料正弦图和使用重建技术得到最终的基材料图像这两个步骤^[5] ...

2019

0.0

... 孙英博等^[6]基于基效应模型, 利用最小二乘算法(least squares, LS)在能谱CT的投影域中进行材料分解 ...

... 在投影分解模型对比实验中, 采用LS算法^[6]、 SR-TF算法^[11]作为对比算法 ...

2017

0.0

... Ducros等^[7]提出了在投影域中对不同材料引入特定的正则项(specific regularization, SR)的投影分解算法, 分解问题使用Gauss-Newton算法迭代求解, 该算法可以从快速线性求解器中受益 ...

... 因此, 根据Ducros等^[7]提出的基于特定材料正则项的投影分解算法, 将分解问题表述为最小化问题求解 ...

2022

0.0

... Cong等^[8]提出了基于单变量优化的双能CT投影分解方法, 该方法结合了多项式方程的解析解和单变量优化来求解多色非线性积分方程, 对双能CT图像进行准确稳定的分解 ...

2012

0.0

... Tang等^[9]提出了基于投影域多尺度分解和惩罚加权最小二乘法进行统计CT降噪的算法 ...

2024

0.0

... Lu等^[10]提出了一种基于低秩和基于相似性正则化(LRSBR)的去噪算法 ...

2023

0.0

... 李佳欣等^[11]在SR的基础上应用张量分解, 提出了基于特定材料和张量分解正则项(SR-TF)的投影分解算法, 并有效抑制了分解噪声 ...

... 在投影分解模型对比实验中, 采用LS算法^[6]、 SR-TF算法^[11]作为对比算法 ...

2019

0.0

... Wu等^[12]提出了基于两步正则化的材料分解算法, 在重建和分解后处理步骤中引入总变分最小化(TVM)作为实现的正则化, 同时抑制了重建和分解两方面的噪声 ...

... 因此, 本文基于文献[12]提出的图像域重建和材料分解两步正则化方法的思想 ...

2025

0.0

... 对于由多种材料组成的非均质物体, 不同材料的衰减系数存在特征性差异^[13] ...

2021

0.0

... 在多方向上施加稀疏性约束, 可以有效地去除噪声和减少单一方向引起的伪影, 同时保留更多细节特征和复杂纹理^[14] ...

2024

0.0

... 3 基于TV4正则项的基材料投影重建受X射线辐射剂量^[15]、扫描范围^[16]、系统噪声^[17]等因素的限制, 对分解后的基材料投影重建时, 也会产生不必要的噪声和条纹伪影干扰, 影响基材料重建图像的质量和细节清晰度 ...

2020

0.0

2023

0.0