引用本文
张伏, 刘志华, 颜宝苹, 王甲甲, 付三玲. 基于BOA-VMD-AWTD算法的TDLAS检测信号降噪方法研究[J]. 光谱学与光谱分析, 2025,45(10): 2915-2921.
ZHANG Fu, LIU Zhi-hua, YAN Bao-ping, WANG Jia-jia, FU San-ling. Research on Noise Reduction Method for TDLAS Signal Detection Based on BOA-VMD-AWTD Algorithm[J]. Spectroscopy and Spectral Analysis, 2025,45(10): 2915-2921.
Doi:10.3964/j.issn.1000-0593(2025)10-2915-07  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于BOA-VMD-AWTD算法的TDLAS检测信号降噪方法研究
张伏1,2, 刘志华1, 颜宝苹1, 王甲甲3, 付三玲4,*
1. 河南科技大学农业装备工程学院, 河南 洛阳 471003
2. 龙门实验室, 河南 洛阳 471000
3. 吉林农业大学工程技术学院, 吉林 长春 130118
4. 河南科技大学物理工程学院, 河南 洛阳 471023
*通讯作者 e-mail: fusanling@126.com

作者简介: 张 伏, 1978年生, 河南科技大学农业装备工程学院教授 e-mail: zhangfu30@126.com

收稿日期: 2025-04-29 修回日期: 2025-06-11
基金: 龙门实验室前沿探索课题(LMQYTSKT032), 国家自然科学基金项目(52075149), 河南省科技攻关计划项目(252102230034), 河南省高等教育教学改革研究与实践项目(2023SJGLX180Y), 河南省研究生教育改革与质量提升工程项目(YJS2025AL49)资助
摘要

为降低可调谐半导体激光吸收光谱技术中二次谐波信号中噪声对信号质量及浓度反演准确性的影响, 本研究以重构信号与参考信号均方误差和相关性损失相结合构建优化目标函数, 采用BOA优化VMD关键参数惩罚因子 α、 分解层数 k、 小波分解层数和阈值系数, 获得最优参数组合, 提高VMD信号分解准确性, 结合本征模态函数能量分布和相关性指标, 设计基于能量-相关性融合的评分机制, 提升算法在不同信号特征下自适应能力。 以CO气体在1 567 nm处吸收光谱为例, 选取EMD、 VMD、 BOA-VMD、 PSO-VMD及BOA-VMD-AWTD五种降噪算法通过仿真对所提方法有效性验证, 仿真结果表明, BOA-VMD-AWTD降噪算法表现最佳, SNR提升14.70 dB, NCC值达0.999 3。 分别采用PSO-VMD、 BOA-VMD、 BOA-VMD-AWTD对试验获得的二次谐波信号降噪处理, 试验结果表明, 0.01%~0.10%浓度范围内不同浓度CO二次谐波降噪后信号幅值线性拟合度 R2达0.999。 为验证BOA-VMD-AWTD算法稳定性, 对预设体积浓度为0.05%CO连续采样, 并对采集浓度数据稳定性分析, 降噪后标准差 σ为0.000 5%, 噪声得到有效抑制, 降噪前后信号均值保持不变, 为TDLAS信号处理提供有效技术支持。

关键词: TDLAS; 变分模态分解; 小波阈值降噪; 蝴蝶优化算法
中图分类号:TH744 文献标志码:A
Research on Noise Reduction Method for TDLAS Signal Detection Based on BOA-VMD-AWTD Algorithm
ZHANG Fu1,2, LIU Zhi-hua1, YAN Bao-ping1, WANG Jia-jia3, FU San-ling4,*
1. College of Agricultural Equipment Engineering, Henan University of Science and Technology, Luoyang 471003, China
2. Longmen Laboratory, Luoyang 471000, China
3. College of Engineering and Technology, Jilin Agricultural University, Changchun 130118, China
4. College of Physics Engineering, Henan University of Science and Technology, Luoyang 471023, China
*Corresponding author
Abstract

To reduce the influence of noise in the second harmonic signal on signal quality and concentration inversion accuracy in tunable semiconductor laser absorption spectroscopy, an optimization objective function was constructed by combining the mean square error and correlation loss between the reconstructed signal and the reference signal. The key parameters of VMD, including the penalty factor α, the number of decomposition layers k, the number of wavelet decomposition layers, and the threshold coefficients, were optimized using the Butterfly Optimization Algorithm (BOA), so that the optimal parameter combinations could be obtained and the accuracy of VMD signal decomposition could be improved. Based on the energy distribution of the intrinsic mode functions and the correlation index, a scoring mechanism that combines energy and correlation was designed to enhance the adaptability of the algorithm under various signal characteristics. In this study, the absorption spectrum of CO gas at 1 567 nm was taken as an example. Five noise reduction algorithms, namely EMD, VMD, BOA-VMD, PSO-VMD, and BOA-VMD-AWTD, were selected to validate the effectiveness of the proposed method through simulation. The simulation results showed that the BOA-VMD-AWTD algorithm achieved the best noise reduction performance, with an SNR improvement of 14.70 dB and an NCC value of 0.999 3. PSO-VMD, BOA-VMD, and BOA-VMD-AWTD were applied to reduce the noise in the second harmonic signals obtained from the experiment. The experimental results demonstrated that the linear fitting coefficient R2 of the signal amplitude after noise reduction, for CO concentrations ranging from 0.01% to 0.10%, reached as high as 0.999. To verify the stability of the BOA-VMD-AWTD algorithm, the second harmonic signals corresponding to a pre-set CO volumetric concentration range of 0.01%~0.10% were denoised, and an NCC value of 0.999 was achieved. Furthermore, to further confirm the stability of the BOA-VMD-AWTD algorithm, a pre-set CO volumetric concentration of 0.05% was continuously sampled, and the stability of the resulting concentration data was analyzed. The standard deviation σ after noise reduction was 0.000 5%, indicating that noise was effectively suppressed, while the mean value of the signal before and after denoising remained unchanged. These results provided effective technical support for TDLAS signal processing.

Keyword: TDLAS; Variational mode decomposition; Wavelet thresholding denoising; Butterfly optimization algorithm
引言

气体污染物是对人体健康危害最大的农业和工业污染物之一, 故精准气体监测技术显得尤为重要。 传统气体检测方法多为接触式, 易污损, 受环境影响较大, 导致检测灵敏度较低[1]。 激光吸收光谱技术的高灵敏度特性在弱吸收信号气体检测中具有明显优势[2]。 在可调谐半导体激光吸收光谱(tunable diode laser absorption spectroscopy, TDLAS)信号处理过程中常受噪声干扰, 有效去除噪声、 提高信号质量是实现高精度气体检测的关键。

传统降噪方法包括低通滤波、 傅里叶变换、 小波变换等[3, 4, 5], 但在处理复杂信号时易造成信号成分缺失, 影响特征提取和后续分析准确性。 经验模态分解(empirical mode decomposition, EMD)[6]作为自适应分解方法, 处理强噪声时易出现模态混叠而影响降噪效果[7]。 针对EMD模态混叠问题, 变分模态分解(variational mode decomposition, VMD)作为自适应非递归分解方法, 可有效抑制模态混叠[8]。 然而, VMD性能依赖于参数合理选取[9]。 为实现VMD参数自适应选取, 提升算法稳定性与鲁棒性, Mao等[10]提出使用粒子群优化算法(particle swarm optimization, PSO)优化VMD, 信噪比(signal noise ratio, SNR)提升4.038 77 dB, 但处理高维复杂问题时易陷入局部最优; 皮晟源等[11]采用改进的鹈鹕优化算法(improved pelican optimization algorithm, IPOA)对VMD算法进行优化, 得到最优参数组合, 有效改善EMD模态混叠问题, 但计算复杂度较高。 Zhu等[12]使用蝴蝶优化算法(butterfly optimization algorithm, BOA)优化VMD对二次谐波信号噪声抑制, 经仿真试验对比, SNR提升9.834 2 dB, 兼具全局和局部探索能力。 小波阈值降噪(wavelet thresholding denoising, WTD)具有良好的时频局部化特性, 但其降噪性能高度依赖分解层数和阈值系数的选取。 为提升降噪性能, 王战等[13]采用新型阈值函数对VMD-WTFD算法改进, 降噪后SNR为17.545 dB, 归一化相关系数(normalized cross correlation, NCC)达0.992 9, 有效平衡了硬阈值函数和软阈值函数的不足; Goh等[14]提出一种改进的自适应小波阈值(adaptive wavelet thresholding denoising, AWTD)降噪方法, 根据信号特性自动调整阈值, 提高降噪鲁棒性。 虽从不同角度提高其在复杂信号处理中适用性, 但单一小波阈值降噪方法难以处理高度非平稳和非线性复杂信号。

针对EMD、 VMD和WTD在处理复杂信号时存在模态混叠和参数依赖性强, 降噪效果不稳定等问题, 复合算法可弥补单一方法不足, 提高降噪性能和稳定性, 但仍存在降噪效果不足且在参数选取时易陷入局部最优等问题, 因此, 本研究利用BOA全局优化的优势, 解决VMD参数选择问题, 结合AWTD自适应阈值降噪, 提高降噪的精确性和自适应性, 为TDLAS信号处理提供一种高效可靠的技术方案。

1 BOA-VMD-AWTD降噪原理
1.1 蝴蝶优化算法

蝴蝶优化算法[15]在复杂优化问题中具有良好的全局搜索能力和收敛性, 在对目标函数、 种群及搜索空间初始化过程中, 保持蝴蝶总数不变, 随机产生不同位置蝴蝶, 根据式(1)计算每只蝴蝶中预留存储其香味和适应度值。

f=cIa(1)

式(1)中, f为每只蝴蝶散发出的香味衡量值; c为感官模态因子; I为香味浓度; a为香味浓度指数。 评估每只蝴蝶个体适应度值大小并更新种群全局最优解, 根据式(2)驱动蝴蝶向最优个体g* 移动, 若无法感知香味时则根据式(3)随机搜索, 每次移动后重新计算适应度值并更新个体历史最优位置及种群全局最优解。

xit+1=xit+(r2g* -xit)fi(2)

式(2)中, xit为迭代次数t中第i个蝴蝶解向量; g* 为当前迭代中最优解; fi为第i个蝴蝶香味。

xit+1=xit+r2xjt-xktfi(3)

式(3)中, xjt和 xkt分别为在搜索空间中第j和第k个蝴蝶。

1.2 降噪算法实现原理

在初始化阶段, 设定优化初始值保证搜索空间的充分探索, 采用BOA优化算法对VMD及小波阈值降噪算法关键参数迭代优化, 寻求VMD及AWTD算法中最优参数。 在优化过程中, 将重构信号与参考信号间均方误差(mean-square error, MSE)及相关损失加权构建目标函数J(x), 目标函数定义如式(4)所示。

J(x)=0.7MSE+0.3(1-|corr(y˙, y)|)(4)

式(4)中, x为输入变量, corr( y˙, y)为重构信号与参考信号相关系数, MSE为重构信号 y˙与参考信号y间平均误差, 如式(5)所示。

MSE=1N∑i=1N(y˙i-yi)2(5)

式(5)中, N为样本总数, y˙i为第i个重构信号值, yi为第i个参考信号值。

获取最佳参数后, VMD对原始信号分解, 得到k个本征模态函数(intrinsic mode function, IMF)分量, 为筛选出对信号贡献较大的IMF分量, 需计算各IMF分量能量占比及参考信号相关性, 并据此构建综合评分函数。 IMF分量能量占比如式(6)所示。

Ri=∑ui2∑∑u2(6)

式(6)中, Ri为第i个IMF分量能量占比, ui为第i个IMF分量信号值, ui2为第i个IMF分量总能量, u2为IMF分量能量之和。 IMF分量与原始信号相关性得分如式(7)所示。

correlationi=|corr(ui, signal)|(7)

式(7)中, correlationi, corr(ui, signal)分别为第i个IMF分量与原始信号相关性得分和相关系数。 根据能量占比及参考信号相关性, 构建加权评分函数, 如式(8)所示。

Si=0.6Ri+0.4correlation(8)

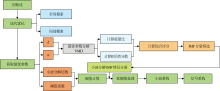
式(8)中, Si为第i个IMF分量综合评分。 根据阈值函数threshold=0.3mean(s)设置选择阈值, 选择得分高于阈值IMF分量信号重构, 对筛选出的IMF分量通过小波变换对各IMF分量多尺度分解, 并通过阈值处理抑制噪声成分, 实现信号降噪, 降噪后信号通过小波重构得到最终输出信号, 如图1所示。

图1 BOA-VMD-AWTD技术路线图Fig.1 BOA-VMD-AWTD technology roadmap

2 仿真与分析
2.1 仿真试验

试验使用MATLAB R2024a软件编写程序仿真TDLAS二次谐波信号, 在温度为296 K、 压强为1 atm条件下, 采用五点差分公式计算信号二阶导数模拟二次谐波信号, 如式(9)所示。

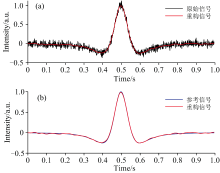
H2(νi)=α(νi+2)-16α(νi+1)+30α(νi)-16α(νi-1)+α(νi-2)12(Δν)2　　(9)

式(9)中, α (ν )为离散输入信号; Δ ν 为频率点间步长; H2(ν )为输出的二次谐波信号, ν i为第i个采样点。 以梯形波为扫描信号, 正弦波为调制信号, 添加高斯白噪声和干涉噪声, 将采样点数设为1 000, 模拟CO气体无噪声和含噪声二次谐波信号, 如图2所示, 原始信号信噪比为13.695 3 dB。

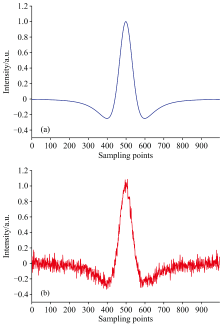图2 二次谐波吸收信号图(a): 原始信号模拟图; (b): 含噪信号模拟图Fig.2 Second harmonic absorption signal(a): Original signal analog diagram; (b): Noisy signal simulation diagram

采用BOA-VMD-AWTD算法对二次谐波信号处理, 将种群数量设定为100, 最大迭代次数为30, 优化维度为4, 经30次迭代优化, 当迭代优化至4次时, 收敛曲线趋于稳定。 通过BOA优化得到最优参数组合, 惩罚因子α 为1091.5, 分解层数k为8, 小波分解层数为7, 阈值系数为1.676 6, 将参数输入到VMD中产生8个IMF分量, 通过构建综合得分函数筛选出高于自适应阈值0.046 4的IMF分量用于重构信号, 将重构信号与原始信号对比, SNR提升14.70 dB, NCC达0.999 3, 如图3所示。

图3 重构信号与原始信号对比图(a): 原始信号与重构信号对比图; (b): 参考信号与重构信号对比图Fig.3 Comparison of reconstructed and original signals(a): Comparison of original and reconstructed signals; (b): Comparison of reference and reconstructed signals

2.2 算法对比分析

为验证降噪方法有效性, 选取EMD、 VMD、 BOA-VMD、 PSO-VMD及BOA-VMD-AWTD五种降噪算法, 经仿真试验对比分析, 降噪效果性能指标如表1所示。

表1 降噪算法性能指标对比表 Table 1 Comparison of performance metrics of denoising algorithms

结果表明, BOA-VMD-AWTD算法SNR值为28.396 4 dB, 较EMD、 VMD、 PSO-VMD和BOA-VMD算法分别提升了25.67%、 17.22%、 3.09%和3.08%; RMSE为0.009 15, 较上述四种算法分别降低了49.22%、 38.80%、 10.03%和9.76%; NCC为0.9993, 较上述四种算法分别提升了0.211%、 0.120%、 0.020%和0.020%, BOA-VMD-AWTD在平衡降噪与信号保真方面表现较优。

3 实验结果与讨论
3.1 试验设备及材料

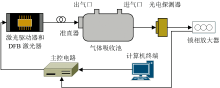
TDLAS气体检测设备配件包括1 567 nm DFB激光光源模块、 气体吸收池、 主控电路、 光电探测模块、 信号放大增益模块等, 选取CO吸收谱线6 381.62 cm-1, 通过激光控制器控制信号输出波长。 经准直器校准后, 进入气体吸收池中发生多次反射, 由光电探测器将光信号转换为电信号, 经锁相放大器处理传输至计算机终端, 如图4所示。

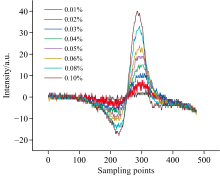
图4 试验设备示意图Fig.4 Schematic diagram of experimental equipment

3.2 数据采集

为使激光器波长与CO气体吸收谱线中心匹配, 设定激光器温度为27.23 ℃, 扫描频率为100 Hz, 调制频率为97 kHz, 电流为80.82 mA。 试验开始前, 采用铂唯YQB-731L流量计, 将体积浓度为0.10% CO气体与高纯氮气混合, 调配CO浓度为0.01%、 0.02%、 0.03%、 0.04%、 0.05%、 0.06%、 0.08%和0.10%, 待气体流量稳定并充分混合后, 通过TDLAS气体检测设备测量CO吸收光谱数据, 结果如图5所示。

图5 不同浓度CO二次谐波信号分布图Fig.5 Distribution of CO second harmonic signals at different concentrations

3.3 处理与分析

在仿真试验阶段由于EMD、 VMD算法降噪效果较差, 难以满足高精度信号处理需求, 为提升降噪适应性与有效性, 分别采用PSO-VMD、 BOA-VMD、 BOA-VMD-AWTD对试验中二次谐波信号降噪处理, 并对降噪后CO浓度与二次谐波吸收强度做线性拟合, 如图6所示。

图6 二次谐波信号吸收强度线性拟合图(a): 原始数据拟合曲线图; (b): PSO-VMD处理后拟合曲线图; (c): BOA-VMD处理后拟合曲线图; (d): BOA-VMD-AWTD处理后拟合曲线图Fig.6 Linear fit of second harmonic absorption intensity(a): Fitted curves for original data; (b): Fitted curves after PSO-VMD treatment; (c): Fitted curves after BOA-VMD treatment; (d): Fitted curves after BOA-VMD-AWTD treatment

经降噪处理后, PSO-VMD使VMD分解更贴合信号特征, 但PSO在复杂搜索空间中易陷入局部最优, BOA-VMD在优化效果上具有更好的全局搜索能力和收敛精度, 有效提升分解质量, BOA-VMD-AWTD通过引入AWTD, 根据不同IMF分量自适应选择最优阈值系数和分解层数, 实现对不同频率成分差异化处理, 增强对不同频带噪声抑制能力, 有效抑制残余噪声, 拟合方程斜率趋于稳定至0.042 06, R2值提升至0.999 19。

3.4 稳定性评估

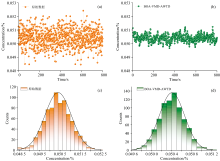
通过前述分析, BOA-VMD-AWTD算法可有效抑制噪声干扰, 展现出优越降噪效果, 优于PSO-VMD和BOA-VMD算法。 为验证BOA-VMD-AWTD算法稳定性, 在800 s 内对预设体积浓度为0.05% CO连续采样, 并对采集数据高斯分布分析, 如图7所示。

图7 数据分布对比图(a): 原始数据分布图; (b): BOA-VMD-AWTD算法处理后数据分布图; (c): 原始数据高斯分布图; (d): BOA-VMD-AWTD算法处理后高斯分布图Fig.7 Comparison of data distribution(a): Original data distribution; (b): Data distribution processed by BOA-VMD-AWTD algorithm; (c): Gaussian distribution of the original data; (d): Gaussian distribution processed by BOA-VMD-AWTD algorithm

从图7中可看出, 原始信号噪声较大, 信号波动明显, 而BOA-VMD-AWTD算法处理后, 数据分布明显收窄, 降噪后数据分布更集中, 由于VMD变分约束条件及AWTD精细化处理, 实现对不同频率成分差异化处理, 确保分解后重构信号与原始信号一致, 相比原始信号, 该算法处理后数据稳定性及测量精度有效提升。 结果表明, 经BOA-VMD-AWTD算法处理, 噪声得到有效抑制, 标准差降低至0.000 551 18%, 降噪前后信号均值几乎保持不变, 如表2所示。

表2 原始数据与BOA-VMD-AWTD处理后数据标准差和均值对比表 Table 2 Standard deviation and mean values of original and processed data by BOA-VMD-AWTD
4 结论

(1)针对TDLAS二次谐波信号中噪声对信号质量及浓度反演准确性的影响, 提出基于BOA-VMD-AWTD算法TDLAS信号降噪方法, 将VMD和小波阈值降噪技术应用于TDLAS气体检测中的二次谐波信号降噪过程, 该方法有效避免了依赖经验选择最优参数问题, 优化后参数组合可更准确地捕捉信号内在特征。

(2)采用基于能量占比和相关性的IMF分量筛选策略, 该策略在保持信号原始形态特征的同时, 可有效抑制噪声成分, 进一步提高信号重构质量。

(3)为验证所提算法适用性, 通过仿真模拟和实际试验验证, 表明该算法在信号降噪、 特征保留及提高测量精度方面有效性。 所提算法在实际应用中展现出较强的稳定性和可靠性, 为TDLAS气体检测信号处理提供有效技术支持。

参考文献
[1] Yan B B, Lü J W, Zhou S Q, et al. Biomass and Bioenergy, 2024, 184: 107198. [本文引用:1]
[2] FANG Xiao-meng, WANG Hua-lai, XU Hui, et al(房孝猛, 王华来, 徐晖, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2024, 44(10): 2909. [本文引用:1]
[3] ZHANG Hao, WANG Ling, ZOU Cai-hong, et al(张浩, 王玲, 邹彩虹, 等). Laser Journal(激光杂志), 2022, 43(7): 31. [本文引用:1]
[4] TIAN Chuan, ZOU Li-chang, RUAN Bin, et al(田川, 邹丽昌, 阮斌, 等). Chinese Journal of Quantum Electronics(量子电子学报), 2021, 38(5): 661. [本文引用:1]
[5] WANG Qi, WANG Xiao-peng, WANG Bo-hui(王祺, 王小鹏, 王博辉). Laser & Optoelectronics Progress(激光与光电子学进展), 2021, 58(20): 79. [本文引用:1]
[6] Wei X Y, Feng G R, Qi T Y, et al. IEEE Sensors Journal, 2022, 22(15): 14959. [本文引用:1]
[7] Gao L, Li X K, Yao Y C, et al. Applied Sciences, 2022, 12(16): 8187. [本文引用:1]
[8] Lian J J, Liu Z, Wang H J, et al. Mechanical Systems and Signal Processing, 2018, 107: 53. [本文引用:1]
[9] Qi G Y, Zhao Z M, Zhang R, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2024, 312: 108807. [本文引用:1]
[10] Mao M H, Chang J, Sun J C, et al. Photonics, 2023, 10(6): 674. [本文引用:1]
[11] PI Sheng-yuan, LIU Mu-yang, CHEN Yu-tian, et al(皮晟源, 刘牧阳, 陈雨田, 等). Proceedings of the CSU-EPSA(电力系统及其自动化学报), 2025. https://doi.org/10.19635/j.cnki.csu-epsa.001580. [本文引用:1]
[12] Zhu X, Liu L F, Wu Q, et al. IEEE Conference Proceedings, 2024, 2024(ICOCN): 1. [本文引用:1]
[13] WANG Zhan, TU Xing-hua, ZHANG Rui-lin(王战, 涂兴华, 张瑞林). Optical Communication Technology(光通信技术), 2024, 48(1): 85. [本文引用:1]
[14] Goh H H, Liao L, Zhang D D, et al. Energies, 2022, 15(9): 3081. [本文引用:1]
[15] Sharma T K, Sahoo A K, Goyal P. Materials Today: Proceedings, 2021, 34(3): 736. [本文引用:1]