引用本文
胡瑞, 李玉军, 焦尚彬, 孙鹏程, 吴晨岩. 基于核马氏聚类的中红外光谱异常样本检测方法研究[J]. 光谱学与光谱分析, 2025,45(10): 2816-2821.
HU Rui, LI Yu-jun, JIAO Shang-bin, SUN Peng-cheng, WU Chen-yan. Kernel Mahalanobis-Driven Clustering for Outlier Detection in Mid-Infrared Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2025,45(10): 2816-2821.
Doi:10.3964/j.issn.1000-0593(2025)10-2816-06  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于核马氏聚类的中红外光谱异常样本检测方法研究
胡瑞1,2, 李玉军1,2,*, 焦尚彬1,2, 孙鹏程1,2, 吴晨岩1,2
1. 西安理工大学自动化与信息工程学院, 陕西 西安 710048
2. 陕西省复杂系统控制与智能信息处理重点实验室, 陕西 西安 710048
*通讯作者 e-mail: leo@xaut.edu.cn

作者简介: 胡 瑞,女, 2001年生,西安理工大学自动化与信息工程学院硕士研究生 e-mail: 18829663501@163.com

收稿日期: 2025-03-19 修回日期: 2025-06-26
基金: 国家自然科学基金项目(62371388)资助
摘要

在烷烃类混合气体红外光谱定量分析中, 人工标定样本制备流程复杂(需精确调控多组分气体浓度、 环境温度及气体压力等参数), 操作偏差容易导致光谱数据与标定浓度的偏离, 产生异常样本。 传统单一异常检测方法难以有效处理高维、 非线性数据中的复杂异常模式。 针对此问题, 提出一种将核马氏距离(KMD)和K-means聚类协同的混合异常检测框架, 创新性地将核化特征映射与动态密度聚类相结合, 克服了在高维样本场景下的矩阵奇异问题及局部异常敏感度不足的缺陷。 利用核马氏距离(KMD)构建非线性高维特征空间, 通过协方差矩阵量化光谱-浓度映射关系异常度, 设置95%置信度阈值( χ2_{0.95})筛选潜在异常候选样本。 结合K-means算法, 将训练集划分为7个优化子簇(依据肘部法则确定), 并通过测试样本到最近质心距离的标准差设置动态阈值剔除异常样本。 最终通过逻辑与(AND)机制实现双阈值联合决策。 实验采用德国Bruker Tensor27光谱仪采集938组样本(波长2.5~25 μm, 分辨率4 cm-1), 以甲烷、 乙烷组分气体为重点分析对象。 通过偏最小二乘(PLS)回归模型验证, 与传统马氏距离(MD)方法对比。 结果表明, 剔除异常样本后, 甲烷浓度预测相对误差(MRE)从38.29%降至18.77%, 较MD方法(30.44%)多降低11.52个百分点; 乙烷MRE从54.51%降至26.03%, 较MD方法(39.42%)多降低13.39个百分点, 模型分析准确度均提高了50%以上。 本研究所提出的方法不仅在理论上突破了高维空间中异常检测的瓶颈, 亦在实际应用中证明了其在复杂气体混合物红外光谱定量分析中的有效性。 相比传统方法, 核马氏距离与K-means聚类的混合检测框架在应对非线性和多维数据时表现出显著的鲁棒性。 该方法为烷烃类混合气体红外光谱定量分析中的异常数据清洗提供了一种可靠有效的解决方案。

关键词: 中红外光谱; 核马氏距离; K-means聚类; 异常检测
中图分类号:O657.33 文献标志码:A
Kernel Mahalanobis-Driven Clustering for Outlier Detection in Mid-Infrared Spectroscopy
HU Rui1,2, LI Yu-jun1,2,*, JIAO Shang-bin1,2, SUN Peng-cheng1,2, WU Chen-yan1,2
1. School of Automation and Information Engineering, Xi'an University of Technology, Xi'an 710048, China
2. Shaanxi Province Complex System Control and Intelligent Information Processing Key Laboratory, Xi'an 710048, China
*Corresponding author
Abstract

In the quantitative analysis of alkane gas mixtures by infrared spectroscopy, the manual calibration sample preparation process is complex (requiring precise control of parameters such as multi-component gas concentration, ambient temperature, and gas pressure), and operational deviations can easily lead to the deviation of spectral data from the calibration concentration, resulting in anomalous samples. The traditional single anomaly detection method is difficult to handle complex anomaly patterns in high-dimensional and nonlinear data effectively. To address this problem, this paper proposes a hybrid anomaly detection framework that synergizes kernel martens distance (KMD) and K-means clustering, which innovatively combines kernelized feature mapping with dynamic density clustering, thereby overcoming the matrix singularity problem and the limitation of insufficient sensitivity to local anomalies in high-dimensional sample scenarios. In this paper, we use the kernel Marginal Distance (KMD) to construct a nonlinear high-dimensional feature space, quantify the anomaly degree of the spectral-concentration mapping relationship through the covariance matrix, and set a 95% confidence threshold ( χ2_{0.95}) to screen potential anomaly candidate samples. Combined with the K-means algorithm, the training set is divided into seven optimisation sub-clusters (determined based on the elbow rule), and a dynamic threshold is set to reject anomalous samples by the standard deviation of the distance from the test sample to the nearest centre of mass. The final dual-threshold joint decision-making is achieved through the logical and (AND) mechanism. The experiment was carried out using a German Bruker Tensor27 spectrometer to collect 938 sets of samples (wavelength 2.5~25 μm, resolution 4 cm-1), with methane and ethane component gases as the focus of analysis. The model was validated by a partial least squares (PLS) regression model and compared with the traditional Marginal Distance (MD) method. The results showed that after excluding the anomalous samples, the relative error (MRE) of methane concentration prediction decreased from 38.29% to 18.77%, which was 11.52 percentage points more than that of the MD method (30.44%). The MRE of ethane decreased from 54.51% to 26.03%, which was 13.39 percentage points more than that of the MD method (39.42%), and the accuracies of the model analyses were both increased by more than 50%. The proposed method not only theoretically breaks the bottleneck of anomaly detection in high-dimensional spaces, but also demonstrates its effectiveness in the quantitative analysis of infrared spectra of complex gas mixtures in practical applications. Compared to traditional methods, the hybrid detection framework of kernel Martens distance and K-means clustering demonstrates significant robustness in handling nonlinear and multidimensional data. The method offers a reliable and effective solution for cleaning anomaly data in the quantitative analysis of infrared spectra of alkane gas mixtures.

Keyword: Mid-infrared spectroscopy; Kernel Mahalanobis distance (KMD); K-means clustering; Anomaly detection
引言

在油气勘探领域, 烷烃类混合气体的红外光谱定量分析是识别薄层油气藏的关键技术之一[1]。 通过红外光谱解析分子特征吸收峰实现浓度定量分析, 其模型鲁棒性依赖标定样本的准确性。 然而, 人工配置混合气体标定样本的过程存在显著挑战: 需精确调控甲烷、 乙烷、 丙烷等多组分气体的浓度比例, 同时维持恒定的温度和压力, 操作流程复杂且耗时。 Griffith在文中指出, 传统制样过程不仅费时且容易受到环境和操作误差的影响, 导致校准光谱的准确性受限, 影响定量分析模型的准确性和稳定性[2], 为此还提出了基于计算合成校准光谱的方法以避免人工制样带来的误差和时间成本。 Platonov等综述了多种标准气体混合物的制备方法, 指出传统的热扩散法和气体提取法在操作复杂性和误差控制方面存在局限性, 而色谱膜法和色谱解吸法则在提高制备精度和稳定性方面具有潜力[3]。 实验表明, 操作人员在高强度作业中易因疲劳或环境干扰(如温湿度波动)导致标定浓度与实际值偏离(即“ 异常样本” ), 而甲烷气体光谱吸收峰位于中红外区, 吸收系数高且受其他组分干扰小, 微小的浓度偏差即可引发显著的光谱响应偏移[4, 5], Kwasny在文献指出, 在1.63~1.69 μ m波段, 甲烷吸收截面达5.13× 10-20 cm2, 远高于水汽和CO2的10-23级别, 这表明甲烷对微小浓度变化高度敏感[6]。 同样Rothman发表于HITRAN2012分子光谱数据库中的数据表明, 甲烷在中红外3.3 μ m波段的吸收线强度约为10-20 cm· molecule-1(cm· molecule-1指每个分子的光学吸收有效面积, 单位是cm2), 该波段内, 甲烷浓度仅微小变化50 ppm, 即可导致吸收峰强度变化超过数个百分点, 从而引起光谱响应的显著偏移。 这一量化数据充分说明了微小浓度偏差对红外光谱定量分析的敏感性和模型稳定性的挑战[7]。 此外, 甲烷浓度常呈现阶梯状或多层次分布特征[8], 导致标定样本分布不均衡, 进一步增加了异常检测的复杂性。 因此, 开发高效、 鲁棒的异常样本检测方法, 对提升光谱定量分析模型的工程适用性至关重要。

传统异常检测方法在复杂工业场景中面临多重瓶颈。 基于距离度量的算法(如马氏距离、 欧氏距离)通常假设数据服从全局线性分布, 难以解析高维非线性结构。 马氏距离需计算协方差矩阵, 但在高维小样本场景下易出现矩阵奇异问题[9], 会导致逆矩阵求解失效; 欧氏距离则因维度灾难导致样本间距离区分度下降。 国内学者近年尝试引入深度学习方法(如自编码器), 但其依赖大规模标注数据, 在样本稀缺场景下易过拟合, 且抗噪性能不足。 除此之外, 基于统计分布的孤立森林算法虽能通过随机划分隔离异常点, 但对噪声敏感且难以适应多层次数据分布[10]。 单一聚类算法(如K-means)虽计算高效, 但在高维异构数据中易受初始质心影响, 误检率较高[11]。

当前虽然已有研究尝试使用结合多种异常检测方法, 例如部分文献提出双重校验的异常样本检测策略, 但将基于高斯核马氏距离与K-means聚类相融合, 并应用于工业混合气体光谱异常识别尚属首次。 针对以上挑战, 本文提出一种核马氏距离与K-means聚类的混合检测框架, 核心思想如下: 通过核函数映射将原始光谱数据投影至高维非线性特征空间, 利用核马氏距离量化光谱特征与浓度关联性的非线性偏差, 克服传统距离算法的维度敏感性问题; 设计动态质心优化机制, 结合聚类边界提升对不均衡分布数据的适应性。 以甲烷组分气体为核心分析对象, 基于偏最小二乘回归模型验证表明, 异常样本剔除后, 甲烷组分气体浓度预测相对误差由38.29%降至18.77%, 该方法为油气勘探中薄层气体异常光谱快速检测提供了高鲁棒性建模支持。

1 实验部分
1.1 混合检测框架

1.1.1 基于特征空间核马氏距离原理

核马氏距离(Kernel Mahalanobis distance, KMD)是一种基于高维特征映射的异常检测方法。 该方法通过核函数将原始数据隐式映射至再生核希尔伯特空间(reproducing Kernel Hilbert space, RKHS), 使得非线性分布数据在高维空间中呈现近似线性可分的特性[12, 13]。 在核函数生成的高维特征空间中, 通过构建协方差矩阵计算样本与正常类分布的马氏距离, KMD能够精准识别偏离正常模式的异常点。 相较于传统距离方法, 有效解决了高维数据、 非线性流形及非高斯分布场景下的异常检测难题。

常见核函数有高斯核、 多项式核、 线性核、 拉普拉斯核和Sigmoid核等[14], 在众多核函数中, 高斯核函数具有强大的非线性映射能力, 适合复杂边界问题。 相较于线性核无法处理非线性边界、 多项式核对阶数敏感、 Sigmoid核收敛不稳定等问题, 相比之下高斯核更加稳定[15]。 高斯核函数在处理中红外光谱数据中表现出优异的局部响应能力和鲁棒性, 适合处理具有复杂扰动特征的烷烃类气体中红外光谱数据。 所以本文采用高斯核函数构建高维特征空间, 将原始非线性模式转换为高维线性可分形式, 同时通过核矩阵隐式计算规避维度灾难。 首先, 定义一个高斯核函数来实现核方法, 高斯核函数定义如式(1)[16]

k(X, Y)=exp-X-Y‖22σ2(1)

式(1)中, ‖ X-Y‖ 表示两样本间的欧氏距离, σ 为高斯核的带宽参数(bandwidth parameter), 带宽参数σ 控制着核函数响应的局部性与泛化能力, σ 值越小, 映射空间越复杂、 越容易过拟合; 反之, 则可能欠拟合。 通过网格搜索结合交叉验证自动选取最优σ 值, 以提升模型稳定性与泛化能力[15]。 其值决定特征空间中局部邻域的尺度, 进而调控核函数的平滑性与数据分布的紧致性。

与传统显式高维映射不同, 通过核矩阵隐式构建特征空间: 训练集核矩阵Ktrain表示训练样本间的相似性; 训练集和测试集之间的核矩阵Ktext反映测试样本与训练样本的跨空间相似性。 核空间均值可直接通过核矩阵的列平均计算, 避免显式操作无限维向量[17]。 计算公式为

μK=1n∑i=1nKtrain(xi, xi)(2)

式(2)中, Ktrain(xi, xi)表示训练数据中第i个样本的自我相似度, n为训练样本的数量。 为分析数据在特征空间中的分布特性, 需构造协方差矩阵[13], 通过核矩阵计算

∑K=1n-1∑i=1n(Ktrain(xi, xi)-μK)(Ktrain(xj, xi)-μK)T(3)

对于测试样本Ktest, 其与训练数据在特征空间中的分布偏离程度可通过核马氏距离度量, 计算公式为[18]

dM(Ktext, μK)=(Ktext-μK)T∑K-1(Ktext-μK)(4)

为判定测试样本的异常性, 需将其核马氏距离(KMD)与训练集的KMD经验分布进行比较。 为设定异常检测阈值, 本文参考 Aggarwal (2017) 提出的分位数设定策略[19], 即使用训练样本得分分布的95%分位点作为阈值判断标准

Threshold=prctile(d(Ktrain), 95)(5)

如果一个测试样本的核马氏距离大于阈值, 则该样本被标记为异常。

1.1.2 K-means聚类算法原理

K-means算法是一种基于目标函数最优化的无监督聚类方法, 其核心在于通过迭代计算将数据集划分为K个互斥子集, 使得每个簇内样本到簇质心的欧氏距离平方和(sum of squared errors, SSE)最小化, 同时实现簇间分离度最大化。 该过程可形式化表示为[11]

SSE=∑k=1K∑xi∈Ck‖xi-μk‖2(6)

式(6)中, Ck为第k个簇的样本集合, μ k为对应簇质心坐标。

K的选取直接影响算法有效性, 不能随意设定, 采用肘部法则(Elbow Method)[20]确定最优参数。 具体过程为: 计算不同K值对应的SSE值, 绘制对应变化折线图并且观察下降速度显著变缓的地方为肘部, 即为最佳聚类数, 从而在聚类效果与模型复杂度之间实现平衡。

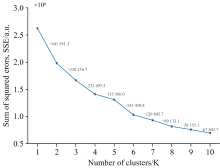
基于原始数据集, 依次对不同聚类数K=1~10执行K-means聚类, 计算对应SSE, 绘制不同K值对应的簇内平方误差和(SSE)分布图如图1所示。

图1 不同K值对应的簇内平方误差和(SSE)分布Fig.1 SSE distribution for varying K values

如图1所示, 横坐标表示聚类数K, 纵坐标表示对应的簇内平方误差和SSE值, 图中SSE值基于原始样本集在不同K值下进行K-means聚类所得结果。 随着K值增加, SSE整体呈递减趋势, 但下降幅度存在较大变化。 例如, 从K=1到K=2, SSE下降了641 581.3; 从K=2到K=3, 下降339 236.7; 从K=4到K=5下降135 586.0; 而从K=5到K=6, 下降量又增至242 458.8; 当K≥ 7时, SSE下降幅度趋于平缓, 表明聚类结构趋于稳定, 过多的聚类数会导致模型复杂度增加但收益减少。 因此, 选择K=7作为最优聚类数, 能在保持聚类精度的同时避免过度分割, 提高模型稳定性与泛化能力。

K-means 算法通过迭代优化实现数据聚类, 主要流程如下:

步骤1: 随机选择K个初始质心(即聚类中心);

步骤2: 基于欧氏距离度量, 将每个样本分配至距离最近的簇;

步骤3: 重新计算各簇样本均值作为新质心;

步骤4: 重复步骤2— 步骤3, 直至质心位置稳定。

异常检测阶段中, 设定阈值Threshold=3× σ min_dist, 其中σ min_dist表示测试样本至最小质心距离的标准差, 当样本距离超过该阈值时, 即被识别为异常值。

1.1.3 基于核马氏距离与K-means的混合异常检测框架

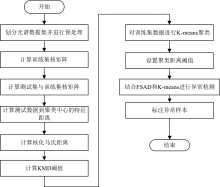
针对复杂高维光谱数据中单一模型方法易误判的难题, 本文提出核马氏距离-聚类混合检测框架, 通过统计假设检验-无监督空间划分双阈值机制筛选异常样本, 能够有效抑制单一方法的误检倾向, 提升对复杂光谱数据的判别置信度。 具体流程见图2所示, 涵盖核矩阵构建、 双阈值协同决策及异常样本标注模块。

图2 混合异常检测框架算法流程图Fig.2 Flow chart of the hybrid anomaly detection framework algosithm

如图2所示, 首先将光谱数据集划分为训练集与测试集并进行归一化处理, 随后通过高斯核函数分别构建训练集核矩阵以及训练集-测试集核矩阵, 并基于核协方差矩阵计算核马氏距离(KMD), 以95%置信度设定KMD阈值; 采用K-means算法对训练集数据进行聚类划分, 计算测试数据到各簇质心的最小距离, 通过3σ 准则动态确定局部空间阈值; 最后, 结合核马氏距离(KMD)与K-means聚类的双阈值机制进行决策, 仅当样本在KMD与簇距离两个独立维度均异常时才最终判定为异常。

1.2 中红外光谱数据采集

红外光谱(infrared spectroscopy, IR)根据波长范围可分为近红外(0.78~2.5 μ m)、 中红外(2.5~25 μ m)及远红外(25~1 000 μ m)三个区域。 鉴于气态分子基频振动吸收峰主要分布于中红外波段(对应波数400~4 000 cm-1), 本研究采用中红外光谱法进行混合气体检测。 该技术基于分子振动能级跃迁产生的特征吸收光谱, 兼具定性与定量分析能力, 被广泛应用于环境监测与化工过程控制等领域。

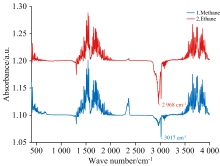
采用德国Bruker公司生产的Tensor27中红外傅里叶光谱仪收集混合气体的红外光谱数据[21]。 共采集有效光谱样本938组, 每组数据包含1 866个波长维度, 波长覆盖范围为2.5~25 μ m, 光谱采样间隔为12 nm。 其典型谱线如图3所示。

图3 甲烷与乙烷单组分气体的红外吸收光谱图Fig.3 Infrared absorption spectra of methane and ethane

图3中纵坐标为吸光度(Absorbance, a.u.), 横坐标为波数(cm-1)。 为了便于观察, 甲烷光谱曲线在原始数据基础上加了0.1的偏移, 乙烷曲线加了0.2的偏移。 甲烷的典型C— H伸缩振动吸收峰位于3 016 cm-1附近, 本实验测得值为3 017 cm-1, 二者高度吻合; 乙烷的主吸收峰出现在2 968 cm-1, 亦与其典型参考值(约2 960 cm-1)基本一致。 这些吸收特征为后续混合气体的定量建模提供了依据。 为构建模型训练与验证数据集, 随机抽取50%样本(n=469)作为训练集Xtrain、 Ytrain, 全部实样本数据(n=938)作为测试集Xtext、 Ytext。

2 结果与讨论
2.1 实验验证

为验证混合异常检测框架的有效性, 基于甲烷、 乙烷组分气体中红外光谱数据集开展实验分析。 为避免过度降维导致关键特征信息损失, 对原始光谱数据进行归一化预处理, 消除量纲差异对核矩阵计算的影响。 核函数选择高斯核; K-means聚类数依据肘部法则确定为7, 确保簇内方差与模型复杂度均衡。 实验验证流程如下:

(1)取50%样本数据(n=469)作为训练集, 全部样本数据(n=938)作为测试集;

(2)计算训练集核矩阵Ktrain以及训练集和测试集之间核矩阵Ktext;

(3)基于核协方差矩阵Σ 计算核马氏距离, 设置异常阈值;

(4)迭代更新簇质心至收敛, 设定簇内距离阈值;

(5)当样本同时超出核距离与簇内距离阈值时判定为异常, 执行三轮迭代剔除以评估稳定性。

2.2 结果分析

为验证本文方法有效性, 采用偏最小二乘(partial least squares, PLS)回归模型评估异常样本剔除效果, 以平均相对误差(mean relative error, MRE)为核心指标, 平均绝对误差(mean absolute error, MAE)与均方根误差(root mean square error, RMSE)为辅助指标。 基于原始数据(未剔除异常样本)建模结果显示, 甲烷组分气体浓度预测结果MRE为38.29%(MAE=2.15%, RMSE=2.56%), 乙烷组分气体浓度预测结果MRE为54.51%(MAE=0.98%, RMSE=1.27%)。

为了进一步验证本文方法的优越性, 以传统马氏距离(MD)为基准方法进行对比实验。 采用相同数据集(50%样本(n=469)作为训练集Xtrain、 Ytrain; 全部实样本数据(n=938)作为测试集Xtext、 Ytext), 设定异常检测阈值为95%置信水平对应的马氏距离分位数。 经三轮异常样本剔除后核马氏聚类(Kernel Mahalanobis-driven clustering, KMDC)方法与传统MD方法对比结果如表1所示。

表1 KMDC与传统MD方法对比分析结果 Table 1 Comparative analysis of KMDC and traditional MD methods

由表1可以看出, 经三轮异常样本剔除后, 传统MD方法使甲烷、 乙烷组分气体分析模型MRE分别由38.29%和54.51降至30.44%和39.42%(降幅分别为20.5%和27.7%); 而KMDC方法使甲烷及乙烷组分气体分析模型的MRE分别从38.29%和54.51降至18.77%和29.49%(降幅分别为51.2%和52.3%)。 上述结果表明, 核马氏距离通过非线性映射提升了高维数据异常敏感性, 联合K-means聚类约束局部密度偏差, 可有效识别并剔除异常样本, 表明本研究可以为烷烃气体光谱定量分析提供了可靠的异常数据清洗方案。

为进一步验证混合框架检测有效性, 对比了通过KMDC方法筛选出来的典型异常样本与正常样本的对比如图4所示。

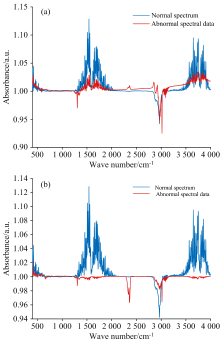图4 筛选出的异常样本光谱对比(a): 样本组1; (b): 样本组2Fig.4 Spectral comparison of the selected abnormal samples and normal samples(a): Sample group 1; (b): Sample group 2

如图4所示, 异常光谱(橙色曲线)在多个波段的吸光度显著偏离正常样本的分布区间, 这种偏离可能与样本制备过程中气体组分异常或仪器噪声干扰相关。 通过混合检测框架识别并剔除此类异常光谱数据, 有效提升了定量模型的预测精度, 验证了该方法在复杂噪声环境下的工程实用性。

3 结论

针对复杂多组分气体红外光谱数据中异常值干扰定量建模的难题, 提出一种基于核马氏距离(KMD)与K-means聚类的混合异常检测框架。 相较于传统方法(如马氏距离、 欧氏距离及单一聚类模型), 本方法的创新性体现在三个层面: 其一, 通过引入高斯核函数隐式映射高维特征空间, 规避传统马氏距离对显式协方差矩阵的强依赖性, 有效解决了高维数据场景下的病态协方差问题; 其二, 结合K-means聚类, 通过逻辑与(AND)操作融合特征空间核马氏距离和聚类, 显著提升了异常判别的鲁棒性; 其三, 构建优化流程, 在三轮异常剔除中实现误差指标的持续收敛。 实验表明, 相较于传统马氏距离方法, 在三轮迭代中使甲烷、 乙烷组分气体浓度预测相对误差(MRE)显著下降。 该方法避免传统马氏距离在高维空间中的不稳定性, 能够同时捕捉数据的非线性特征并减少聚类时对异常值的敏感性, 显著提升了复杂多组分气体光谱数据的异常检测精度, 为高噪声场景下的定量建模提供了可靠的技术支撑。 该方法为石油化工、 环境监测等领域中高噪声光谱数据的异常检测与模型优化提供了新思路。 尽管本文提出的核马氏距离与K-means聚类融合方法在多组分气体光谱异常检测中展现出良好性能, 但仍存在一定局限性。 首先, 该方法主要针对具有高维非线性分布的数据结构设计, 对于结构简单或低维线性分布的数据适应性有限; 其次, 在大规模或高维光谱数据下, 核矩阵的计算复杂度较高, 可能成为工程应用的瓶颈; 此外, 当前使用的K-means聚类虽应用广泛, 但存在鲁棒性不足的问题。 未来可考虑融合更优聚类算法, 进一步增强对复杂数据结构下异常样本的识别能力。 未来研究可从以下方向展开: 引入自适应聚类或图神经网络以增强对时变数据的建模能力; 在迁移学习框架下评估该方法在其他工业场景(如尾气排放监测)中的适用性, 进一步提升其实用性与泛化能力。

参考文献
[1] JING Wen-feng, YAN Rong-hui, CHEN Zhong-pu, et al(荆文峰, 阎荣辉, 陈中普, 等). Mud Logging Engineering(录井工程), 2019, 30(3): 124. [本文引用:1]
[2] Griffith D W T. Applied Spectroscopy, 1996, 50(1): 59. [本文引用:1]
[3] Platonov I A, Rodinkov O V, Gorbacheva A R, et al. Journal of Analytical Chemistry, 2018, 73(2): 109. [本文引用:1]
[4] WANG Zhi-qi, YANG Hong-jie, DONG Xu-bin, et al(汪智琦, 杨洪杰, 董旭斌, 等). Instrumentation User(仪器仪表用户), 2019, 26(11): 6. [本文引用:1]
[5] ZHANG Xin, ZHANG Zheng-dong, DU Biao, et al(张鑫, 张正东, 杜彪, 等). Chemical Reagents(化学试剂), 2024, 46(8): 59. [本文引用:1]
[6] Kwasny M, Bombalska A. Sensors, 2023, 23(5): 2834. [本文引用:1]
[7] Rothman L S, Gordon I E, Babikov Y, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2013, 130: 4. [本文引用:1]
[8] LI Shao-min, SUN Li-qun(李绍民, 孙利群). Acta Physica Sinica(物理学报), 2023, 72(1): 010701. [本文引用:1]
[9] WANG Xing, HUANG Xiao-yu, LIU Xuan-pu, et al(汪星, 黄小瑜, 刘瑄璞, 等). Journal of Xidian University(西安电子科技大学学报), 2018, 45(4): 106. [本文引用:1]
[10] LI Shu-yuan, ZHAO Jian, ZHAO Yi-jun(李书缘, 赵俭, 赵乂鋆). Metrology & Measurement Technology(计测技术), 2024, 44(1): 80. [本文引用:1]
[11] LI Tong, ZHAI Yong-nan, HUA Ying-fan(李彤, 翟永南, 华英凡). Systems Engineering-Theory & Practice(系统工程理论与实践), 2024, 44(2): 752. [本文引用:2]
[12] Gu H, Wang L. International Journal of Chemical Engineering, 2022, 2022: 8460463(doi: 101155/2022/8460463). [本文引用:1]
[13] Muand et K, Fukumizu K, Sriperumbudur B, et al. Foundations and Trends® in Machine Learning, 2017, 10(1-2): 1: 101561/2200000060. [本文引用:2]
[14] WEI Meng-sha, GONG Yun, ZHANG Xiao-yu, et al(卫梦莎, 龚云, 张小宇, 等). Bulletin of Surveying and Mapping(测绘通报), 2024, (9): 117. [本文引用:1]
[15] Chang C C, Lin C J. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 101145/1961189. 1961199. [本文引用:2]
[16] Schölkopf B, Smola A J. Cambridge, MA: MIT Press, 2001. doi: DOI:10.7551/mitpress/4175.001.0001. [本文引用:1]
[17] Hoffmann H. Pattern Recognition, 2007, 40(3): 863. [本文引用:1]
[18] De Maesschalck R, Jouan-Rimbaud D, Massart D L. Chemometrics and Intelligent Laboratory Systems, 2000, 50(1): 1. [本文引用:1]
[19] Aggarwal C C. Cham: Springer, 2017. [本文引用:1]
[20] Thorndike R L. Psychometrika, 1953, 18(4): 267. [本文引用:1]
[21] LI Yu-jun, TANG Xiao-jun, LIU Jun-hua(李玉军, 汤晓君, 刘君华). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2010, 30(3): 774. [本文引用:1]