引用本文
李译铎, 冯志芳, 陈东明, 张倩, 姚宁, 张平, 陶亚萍, 赵文来, 杜建宾. 外电场作用下1,5-二硝基萘的分子结构和光谱研究[J]. 光谱学与光谱分析, 2025,45(10): 2760-2766.
LI Yi-duo, FENG Zhi-fang, CHEN Dong-ming, ZHANG Qian, YAO Ning, ZHANG Ping, TAO Ya-ping, ZHAO Wen-lai, DU Jian-bin. External Electric Field Effects on the Molecular Structure and Spectra of 1,5-Dinitronaphthalene[J]. Spectroscopy and Spectral Analysis, 2025,45(10): 2760-2766.
Doi:10.3964/j.issn.1000-0593(2025)10-2760-07  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
外电场作用下1,5-二硝基萘的分子结构和光谱研究
李译铎1, 冯志芳1, 陈东明2, 张倩1, 姚宁1, 张平1, 陶亚萍3, 赵文来4, 杜建宾1,*
1. 廊坊师范学院理学院, 河北 廊坊 065000
2. 北华航天工业学院机电工程学院, 河北 廊坊 065000
3. 洛阳师范学院物理与电子信息学院, 河北 洛阳 471934
4. 清华大学计算机科学与技术系, 北京 100084
*通讯作者 e-mail: dujianbinfzf@tju.edu.cn

作者简介: 李译铎, 2003年生,廊坊师范学院理学院本科生 e-mail: 2275329440@qq.com

收稿日期: 2025-04-22 修回日期: 2025-07-15
基金: 国家自然科学基金项目(NSFC22174098)资助
摘要

1,5-二硝基萘(DNN)是一种非常重要的化工原材料, 在多个领域被广泛采用, 但其分子结构和光谱的外场效应还未见报道。 因此, 基于密度泛函理论(DFT)中的B3LYP方法, 在def2-TZVP基组水平上, 对不同外电场下分子的基态几何结构进行了优化, 并计算了其红外(IR)光谱。 在此基础上, 基于含时密度泛函理论(TDDFT)研究了外电场对DNN分子紫外-可见(UV-Vis)光谱的影响。 结果表明: 在0~0.02 a.u.外电场作用下, DNN分子的几何构型改变明显; 诱导偶极矩与永久偶极矩的方向相同, 总偶极矩随着外电场的增强而增大; 分子总能量随着外电场的增强而降低; 1 348和1 579 cm-1处的红外吸收峰分别归属于N17-O18和N17-O19、 N20-O21和N20-O22的对称、 非对称伸缩振动, 两者在外电场作用下都发生了能级劈裂, 振动斯塔克效应明显; 分子在200、 235和353 nm附近出现3个紫外吸收峰, 200和235 nm的吸收峰分别归属于E1和E2带, 是由苯型体系中的π—π*跃迁所产生, 353 nm的吸收峰归属于B带, 是由芳香族化合物中的π—π*跃迁引起的; 在外电场作用下, UV-Vis吸收峰出现红移, 摩尔系数先增大后减小; 在分子的二维UV-Vis光谱中, 同步图对角线上200 nm处形成一个较强自相关峰, 证明该峰对外电场变化非常敏感。 总之, 外电场对DNN分子的影响十分显著。 这项工作为DNN的各种潜在应用提供了一定的理论指导, 同时也对萘的其他硝化产物的研究有参考价值。

关键词: 1; 5-二硝基萘; 外电场; DFT; 光谱
中图分类号:O561.3 文献标志码:A
External Electric Field Effects on the Molecular Structure and Spectra of 1,5-Dinitronaphthalene
LI Yi-duo1, FENG Zhi-fang1, CHEN Dong-ming2, ZHANG Qian1, YAO Ning1, ZHANG Ping1, TAO Ya-ping3, ZHAO Wen-lai4, DU Jian-bin1,*
1. College of Science, Langfang Normal University, Langfang 065000, China
2. School of Mechanical and Electrical Engineering, North China Institute of Aerospace Engineering, Langfang 065000, China
3. College of Physics and Electronic Information, Luoyang Normal University, Luoyang 471934, China
4. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China
*Corresponding author
Abstract

1,5-dinitronaphthalene (DNN) is an important chemical raw material, widely used in various fields. To study the effect of external electric field (EEF) on DNN, the B3LYP of density functional theory (DFT) is employed to optimize the ground state structure of DNN at the def2-TZVP basis set level, and its infrared (IR) spectra are obtained. Based on this, time-dependent density functional theory (TDDFT) is employed to calculate the change in UV-Vis spectra of DNN under EEF. The range of the electrostatic field is 0~0.02 a.u. in this work. The results show that the geometric configuration of DNN strongly depends on changes in EEF. The dipole moment increases with the enhancement of EEF, while the change in total energy is opposite. The IR spectra undergo energy splitting, and the vibration Stark effect is obvious. The absorption peaks of the UV-Vis spectra exhibit a red shift; the molar coefficients initially increase and then decrease. In the two-dimensional UV-Vis spectrum of DNN, there is a strong autocorrelation peak at 200 nm on the diagonal of the synchronous graph, which indicates that the peak is very sensitive to changes in EEF. In summary, EEF has a significant impact on DNN. This work provides theoretical guidance for various potential applications of DNN, and also has reference value for the study of other nitration products of naphthalene.

Keyword: 1; 5-dinitronaphthalene; External electric field; DFT; Spectra
引言

硝基芳香族化合物在精细化工行业中占据重要地位, 被广泛应用于香料、 医药、 塑料以及炸药制造等领域。 其中, 1, 5-二硝基萘(1, 5-dinitronaphthalene, DNN)是制备染料、 聚氨酯和荧光试剂等的主要原材料, 具有重大的经济价值, 因此DNN成为近年来研究的热点。 Xiong等开发了一种镍颗粒催化剂, 它在100 ℃的条件下能使DNN的氢化率达到95.8%[1, 2]。 严家其发明了一种温和、 高效催化硝化1-硝基萘或萘制备DNN的方法, 该方法相对于传统的“ 硝-硫混酸” 的硝化法更加环保。 研究人员将DNN作为有机阴极, 其表现出超高能量密度[3]。 日本的研究小组则报道了光照会增加多种硝基多环芳烃的毒性, 但DNN是个特例[4]。

当外电场作用于物质分子时, 会伴随着一系列新的现象出现, 如分子键长、 键角、 二面角等几何结构的变化, 密立根电荷的转移[5], 红外光谱的振动斯塔克效应[6]以及异质结能带排列的改变[7]等。 将电场作用于水-油界面, 电场会影响原油固有表面活性成分(沥青质)的吸附[8]。 Wu等采用密度泛函理论(density functional theory, DFT)和含时密度泛函理论(time-dependent density functional theory, TDDFT)方法研究了外电场对分子马达的影响, 结果表明外电场对提高分子马达的性能潜力巨大[9]。 德国的科研人员将外电场作用于P3HT(poly 3-hexylthiophene-2, 5-diyl)的带隙, 证明了外部电场能够加速复合过程的速率[10]。 北京工业大学的研究团队证实, 当对纳米结构表面的固-液界面施加外电场作用时, 会产生电润湿和热流密度增大等现象[11]。 安桓等研究了外电场作用下对二溴苯的光谱特性和解离特性, 结果显示分子的基态几何结构、 光谱特性、 势能曲线及势能面均发生较大改变[12]。 外电场作用下二苯基甲烷分子结构变化明显, 红外光谱振动斯塔克效应显著[6]。 陶亚萍等基于DFT对噻克索酮分子的外场效应进行了计算, 结果表明分子的键长、 键角、 总能量、 偶极矩、 电荷和芳香性都发生了变化[13]。 截至目前, DNN分子结构和光谱的外场效应还未见报道。

密度泛函理论基于量子力学, 使用电子密度大大提高了计算效率, 被广泛应用于计算物理和计算化学的多个领域。 在此, 各种电场下DNN基态几何结构的优化由密度泛函理论B3LYP[14, 15, 16]/def2-TZVP[17, 18, 19, 20, 21, 22]方法完成。 在此基础上, 基于相同的方法计算了DNN分子的IR光谱。 最后, 计算DNN分子激发态的任务在def2-TZVP基组水平上采用TDDFT[16]完成。 这项工作对DNN的潜在应用有指导意义。

1 理论和计算方法

由于外电场的存在, DNN分子的哈密顿量H由两部分组成

H=H0+Hint(1)

式(1)中, H0为无外部电场时的哈密顿量, Hint为外电场和分子体系相互作用下的微扰量。 在偶极近似的情况下, 体系的微扰量可表示为

Hint=-μ·F(2)

式(2)中, μ 为分子的偶极矩, F为外加电场。

当外部电场存在时, 忽略极化效应的情况下[23]

Eexc(F)=Eexc(0)-Δμ·F-12ΔαF2(3)

式(3)中, Eexc为分子体系的激发能, Δ α 为极化率的改变量, Δ μ 是偶极矩的改变量, 此处为诱导偶极矩。 Δ α 和Δ μ 之间的关系为

Δμ=Δα·F(4)

如果Δ μ 为正, 则可以得出结论Eexc(F)小于Eexc(0), 意味着引入外电场导致吸收峰的波长增加, 即吸收峰出现了红移。 永久偶极矩是无外电场时分子内部电荷的不对称分布引起的, 红外吸收取决于分子振动过程中偶极矩的变化。 跃迁偶极矩是电子从一个能级跃迁到另一个能级时分子偶极矩的变化, 它决定了电子从基态跃迁到激发态的概率和强度, 较大的跃迁偶极矩意味着更强的UV-Vis吸收。

振子强度f1u由式(5)给出[24]

glf1u=8π2mca02σ3hS=3.03966×10-6σS(5)

式(5)中, gl为加权因子, 此处等于1; S为线强度, 它的单位为原子单位(e2 a02); σ 为能量。 在该研究中, 将微扰项Hint加入到薛定谔方程的哈密顿量中, 再由Gaussian程序计算相关物理量, 全部计算由Gaussian16软件包完成。 为了研究DNN分子的外场效应, 沿x轴方向施加了一系列的外电场0~0.02 a.u.(0~1.028 5× 1010 V· m-1)。 在def2-TZVP基组水平上, 通过混合密度泛函方法B3LYP优化了不同的外电场作用下DNN分子的基态几何构型, 无外电场时分子的结构如图1所示。 在此基础上通过计算分子的振动频率, 得到了DNN的IR光谱。 最后通过TDDFT在def2-TZVP基组水平上计算了DNN的前26个激发态, 得到了其UV-Vis光谱。

图1 无外电场时DNN的分子结构图中原子上的数字为原子序号Fig.1 The structure of DNN in the absence of an external electric fieldThe number on the atom represents the atomic order number

2 结果与讨论
2.1 不同外电场下DNN的分子结构

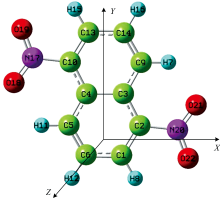
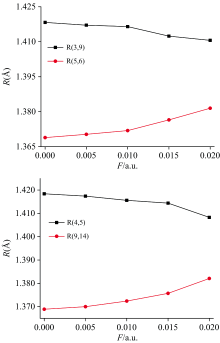
采用B3LYP方法结合def2-TZVP基组优化了DNN不同电场下的分子结构, 得到了其稳定的构型, 部分键长随电场的变化如表1和图2所示。 可以看出, 由于外电场的引入, 分子结构发生了明显的改变。 随着外电场的增强, R(3, 9)和R(4, 5)逐渐减小, 而R(5, 6)和R(9, 14)逐渐增大, 这些变化是由于分子内电场和外电场的叠加造成的[23]。 随着外电场的增强, 电荷发生了转移(如表2和图7所示), 电子云出现了重排, 内电场和外电场的叠加使得3C和9C、 4C和5C间的作用力增强, 从而其键长减小; 而内电场和外电场的叠加使得5C和6C、 9C和14C间的作用力减弱, 从而其键长增大。

表1 不同电场强度F/a.u.下DNN分子的部分键长R/Å , 其中括号内的数字为原子序号 Table 1 The bond lengths (unit: Å ) of some atoms in DNN under different electric field strengths (unit: a.u.), the number in parentheses represents the atomic order number

图2 外电场F/a.u.与DNN分子部分键长R/Å 的关系(其中括号内的数字为原子序号)Fig.2 The relationship between external electric fields (unit: a.u.) and a part of bond lengths (unit: Å )of DNN (the number in parentheses represents the atomic order number)

表2 不同电场下DNN部分原子的电荷Q/a.u. Table 2 The charges(unit: a.u.)of some atoms in DNN under different electric fields

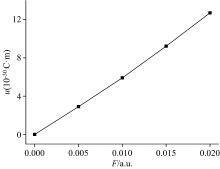
通过高斯计算得到的偶极矩是由永久偶极矩和外电场诱导出的偶极矩两部分组成。 当诱导偶极矩与永久偶极矩的方向相反时, 总偶极矩会先减小后增大; 而当诱导偶极矩与永久偶极矩的方向相同时, 总偶极矩会随着外电场的增强逐渐增大。 很显然, DNN分子即属于后者, 如图3所示。 在外电场的作用下, DNN分子中的电子发生了偏移, 使得正负电荷中心分离, 形成了诱导偶极矩, 如图7所示。 分子的偶极矩越大意味着分子的极性越强[25], 计算结果表明, 外电场的加入增强了DNN分子的极性。

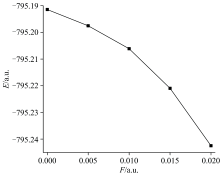
图3 DNN分子偶极矩与电场的关系Fig.3 The relationship between dipole moments of DNN and electric fields

随着分子结构和偶极矩的变化, DNN分子的总能量呈现出明显下降的趋势, 如图4所示。 无外电场存在时, 其分子的基态总能量为-795.191 4 a.u., 随着外电场的增强分子的基态总能量逐渐减小。 当外电场增加到0.020 a.u.时, 其总能量减小为-795.242 5 a.u.。 这是由于外电场的诱导使得DNN分子的共轭体系发生了电子离域, 降低了体系的能量。 随着分子偶极矩的增大, 由式(2)可知微扰项减小, 进而使得分子的总能量下降。 能量越低意味着分子结构越稳固, 也就是外电场的引入增加了DNN分子的稳定性。

图4 DNN分子总能量与电场的关系Fig.4 The relationship between total energies of DNN and electric fields

2.2 不同外电场下DNN分子的红外光谱

通过计算不同电场下DNN分子的振动频率得到了其IR光谱[26], 由于强吸收峰全部位于600~1 800 cm-1, 因此图5只给出了该波数范围的IR光谱(括号外为吸收峰的波数, 括号内为摩尔吸收系数)。 不存在外电场时, 强吸收峰出现在902、 1 348和1 579 cm-1附近, 其中波数为902 cm-1的吸收峰为N17-O18和N17-O19、 N20-O21和N20-O22的面内剪式振动所产生, 1 348 cm-1处的吸收峰为N17-O18和N17-O19、 N20-O21和N20-O22的对称伸缩振动所产生, 而1 579 cm-1的吸收峰归属于N17-O18和N17-O19、 N20-O21和N20-O22的非对称伸缩振动。 文献[27]报道了使用BRUKER IFS-66 V傅里叶变换红外光谱仪测得的N— O对称伸缩振动的波数为1 347 cm-1, 与本文的计算结果基本一致, 这证明了本研究方法的可靠性。 需要注意的是, DNN分子包含两个硝基, 它的红外强吸收峰均归属于硝基的伸缩振动, 与其他有机分子C— H和O— H伸缩振动产生的吸收峰相比[6, 26], 硝基吸收峰的波长更长。 这是由于N=O的键长更长, 振动频率更小的原因。

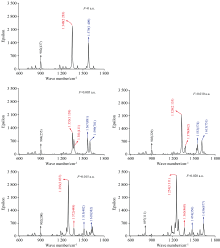图5 真空中不同电场下DNN分子的红外光谱, 其中同一颜色代表同一振动形成的吸收峰Fig.5 The IR spectra of DNN under different external electric fields in vacuum, the same color represents the absorption peak formed by the same vibration

在外电场作用下, 902 cm-1处的吸收峰在电场较弱时位置变化并不明显, 直到电场增加到0.02 a.u.时才出现较小的红移, 但该吸收峰的摩尔吸收系数随着外电场的加入出现了明显的下降, 这说明外电场对N— O剪式振动的频率影响很小, 但对其振幅改变较大。 外电场的引入使得1 348 cm-1处的吸收峰出现了能级劈裂, 在0.005 a.u.时形成了1 353和1 381 cm-1两个吸收峰, 他们分别对应于N17-O18和N17-O19、 N20-O21和N20-O22的对称伸缩振动。 随着外电场的增强两个吸收峰都发生了红移, 1 353 cm-1减小到1 254 cm-1, 1 381 cm-1减小到1 365 cm-1, 可以看出随着外电场的增强两个吸收峰劈裂的间距在增大。 伴随着吸收峰的红移, 1 353 cm-1峰的摩尔吸收系数逐渐增大, 而1 381 cm-1 的摩尔系数变化不明显。 这说明DNN分子结构的变化导致N17-O18和N17-O19、 N20-O21和N20-O22对称伸缩振动的频率减小, N17-O18和N17-O19对称伸缩振动的振幅增大, 而N20-O21和N20-O22的振幅变化不明显。 和1 348 cm-1峰类似, 在外电场的作用下1 579 cm-1峰也出现了能级劈裂, 在0.005 a.u.时形成了1 567和1 599 cm-1两个峰, 他们分别对应于N17-O18和N17-O19、 N20-O21和N20-O22的非对称伸缩振动。 1 567 cm-1峰随电场增强出现红移, 而1 599 cm-1峰出现了蓝移, 两者之间的间距越来越大, 这说明分子结构的变化使得N17-O18和N17-O19非对称伸缩的频率减小, 而N20-O21和N20-O22非对称伸缩的频率增大。 综上所述, 外电场的引入使得DNN分子出现了明显的振动斯塔克效应, 可见DNN分子对外电场非常敏感。

2.3 不同外电场下DNN分子的UV-Vis光谱

在DNN分子基态几何结构优化的基础上, 采用含时密度泛函理论计算了不同电场下分子的前26个激发态, 得到了其UV-Vis光谱, 如图6所示。 当无外电场时, DNN分子有3个吸收峰, 分别位于200、 235和353 nm附近, 其摩尔吸收系数分别为17 137、 12 097和9 714 L· mol-1· cm-1。 200和235 nm处的吸收峰分别归属于E1和E2带, 是由苯型体系中的π — π * 跃迁所产生。 353 nm处的吸收峰归属于B带, 是由芳香族化合物中的π — π * 跃迁引起的。 与二苯甲烷的UV-Vis光谱相比[6], DNN的E带吸收峰波长更长, 摩尔吸收系数更小, 这是由于奈环连接硝基后形成了大π 键, 键的平均化使得电子更容易被激发, 即激发电子所需的能量更小, 吸收峰的波长更长; 奈环形成大π 键也使得奈环上电子云的密度减小(如DNN和二苯甲烷的前线轨道图所示), 跃迁的电子数减少, 从而吸收峰的摩尔吸收系数更小。

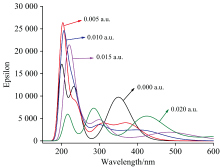图6 真空中DNN分子在不同外加电场下的UV-Vis光谱Fig.6 UV-Vis spectra of DNN under different external electric fields in vacuum

不同电场下DNN分子的UV-Vis光谱如图6所示, 在0~0.02 a.u.电场范围内, 随着外电场的增强, 各吸收峰向长波方向移动, 即发生了红移。 200、 235和353 nm三个吸收峰分别移动到了218、 283和434 nm附近, 分别红移了18、 48和81 nm, 这是由于随着外电场的增大, 分子内电荷发生了转移, 苯环上的电子云密度明显下降(如图7所示), 使得共轭的苯型体系中大π 键变弱, 跃的电子跃迁所需能量减小、 波长增大。 由图3可知Δ μ > 0, 由式(3)和式(4)可得到Eexc(F)< Eexc(0), 也就是在外电场作用下激发态的能量降低、 频率减小、 波长增大, 即波峰发生了红移。 伴随着吸收峰的红移, 其摩尔吸收系数先增大后减小。 外电场为0.005 a.u.时最强吸收峰从无电场时的17 137 L· mol-1· cm-1增大到25 947 L· mol-1· cm-1, 但随着外电场进一步增强, 吸收峰的摩尔吸收系数开始下降, 这是由于刚引入外电场时, 苯型体系中π — π * 电子跃迁所需能量减小, 电子跃迁更容易发生, 也就使得跃迁的电子数增多, 所以此时摩尔吸收系数增大, 但随着外电场继续增强, 苯环上的电子云密度下降, 使得跃迁的电子数减少, 因此摩尔吸收系数减小。

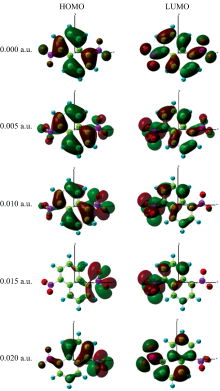图7 不同外电场下DNN分子的前线轨道Fig.7 The excited state frontier orbital diagram of DNN under different electric fields

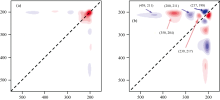
与一维光谱相比, 二维光谱具有分辨率高、 能够解析动态过程的优点。 为了更好的理解外场效应, 我们研究了DNN分子的二维UV-Vis光谱[28]。 在0~0.025 a.u.电场范围内每隔0.002 5 a.u.计算一次UV-Vis光谱, 共得到11组数据。 然后采用2Dshige[2Dshige (c) ShigeakiMorita, Kwansei-GakuinUniversity, Japan, 2004— 2005][29]处理这11组一维光谱数据, 即可得到DNN的二维UV-Vis光谱, 如图8所示。 在图8(a)中, 对角线上200 nm处形成一个较强自相关峰, 说明该峰对电场变化非常敏感, 光谱强度变化也主要集中在该峰附近。 在图8(b)中, 在(239, 217) nm和(350, 204) nm处形成两个正交叉峰, 在(217, 198)、 (280, 211)和(439, 211) nm处形成三个负交叉峰, 说明吸收峰的变化239 nm快于217、 350 nm快于204 nm、 217 nm慢于198 nm、 280 nm慢于211 nm、 439 nm慢于211 nm。 异步交叉峰的出现表明这些吸收峰归属于不同性质的电子跃迁。

图8 DNN分子在不同外电场下的二维UV-Vis光谱(a): 同步图; (b): 异步图Fig.8 The two-dimensional UV-Vis spectra of DNN under different electric external fields(a): Synchronous; (b): Asynchronous

3 结论

(1)基于DFT研究了不同外电场对DNN分子结构和IR光谱的影响, 结果表明: 外电场与内电场的叠加改变了分子的几何结构; 外电场的引入使得分子电偶极矩增大、 分子总能量减小, IR光谱的振动斯塔克效应明显。

(2)基于TDDFT研究了不同外电场对DNN分子UV-Vis光谱的影响, 结果表明: 外电场的引入使得分子内电荷发生了转移, 光谱的紫外吸收峰红移显著, 摩尔吸收系数先增大后减小。

综上可知, 外电场对DNN分子的影响十分显著。 这项工作为DNN的各种潜在应用提供了一定的理论指导, 同时也对萘的其他硝化产物的研究有参考价值。

参考文献
[1] Xiong W, Zhou S S, Zhao Z Y, et al. Frontiers of Chemical Science and Engineering, 2021, 15(4): 998. [本文引用:1]
[2] Yan J Q, You K Y, Yin J H, et al. Surfaces and Interfaces, 2023, 36: 102501. [本文引用:1]
[3] Chen Z F, Su H, Sun P F, et al. Proceedings of the National Academy of Sciences of the United States of America, 2022, 119(6): e2116775119. [本文引用:1]
[4] Onduka T, Ojima D, Ito K, et al. Chemosphere, 2017, 169: 596. [本文引用:1]
[5] DU Jian-bin, FENG Zhi-fang, ZHANG Qian, et al (杜建宾, 冯志芳, 张倩, 等). Acta Physica Sinica(物理学报), 2019, 68(17): 173101. [本文引用:1]
[6] Zhang Q, Feng Z F, Niu Y L, et al. Chemical Physics Letters, 2024, 849: 141419. [本文引用:4]
[7] LIU Chen-xi, PANG Guo-wang, PAN Duo-qiao, et al(刘晨曦, 庞国旺, 潘多桥, 等). Acta Physica Sinica(物理学报), 2022, 71(9): 097301. [本文引用:1]
[8] Sjoblom J, Mhatre S, Simon S, et al. Advances in Colloid and Interface Science, 2021, 294: 102455. [本文引用:1]
[9] Wu L T, Nachimuthu S, Kaleta J, et al. Journal of Chemical Physics, 2024, 161: 214301. [本文引用:1]
[10] Rana D, Ranga A K, Materny A. Physical Chemistry Chemical Physics, 2025, 27: 4475. [本文引用:1]
[11] QI Kai, ZHU Xing-guang, WANG Jun, et al(齐凯, 朱星光, 王军, 等). Acta Physica Sinica(物理学报), 2024, 73(15): 156801. [本文引用:1]
[12] AN Huan, YAN Hao-kui, XIANG Mei, et al(安桓, 闫好奎, 向梅, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(2): 405. [本文引用:1]
[13] Tao Y P, Wang Q, Sun K X, et al. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2020, 231: 118108. [本文引用:1]
[14] Peng X G, Cao W J, Hu Z B, et al. Journal of Chemical Physics, 2024, 160: 054308. [本文引用:1]
[15] Mori T. Angewand te Chemie International Edition, 2024, 63: e202319702. [本文引用:1]
[16] Sharma P, Ranjan P, Chakraborty T. Materials Today Sustainability, 2024, 26: 100791. [本文引用:2]
[17] Burguera S, Sahu A K, Chavez Romero M J, et al. Physical Chemistry Chemical Physics, 2024, 26: 18606. [本文引用:1]
[18] Duan J J, Yang X Q, Li R N, et al. Journal of the American Chemical Society, 2024, 146: 13025. [本文引用:1]
[19] Diao K, Shi S P, Song Y, et al. International Journal of Hydrogen Energy, 2024, 67: 1173. [本文引用:1]
[20] Roy S, Durholt J P, Asche T S, et al. Nature Communications, 2024, 15: 6030. [本文引用:1]
[21] Sameera W M C, Senevirathne B, Andersson S, et al. The Journal of Physical Chemistry A, 2021, 125: 387. [本文引用:1]
[22] Tao Y P, Han L G, Sun A D, et al. Crystals, 2020, 10: 19. [本文引用:1]
[23] Grozema F C, Telesca R, Jonkman H T, et al. Journal of Chemical Physics, 2001, 115(21): 10014. [本文引用:2]
[24] Wu D L, Tan B, Wan H J, et al. Chinese Physics B, 2013, 22(12): 123101. [本文引用:1]
[25] Lin H, Liu Y Z, Yin W Y, et al. Journal of Theoretical and Computational Chemistry, 2018, 17(4) 1850029. [本文引用:1]
[26] Du J B, Yao N, Ma X Y, et al. Chemical Physics Letters, 2023, 810: 140176. [本文引用:2]
[27] Arivazhagan M, Krishnakumar V, Xavier R J, et al. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2009, 72: 941. [本文引用:1]
[28] van Adrichem K E, Jansen T L C. Journal of Chemical Theory and Computation, 2022, 18: 3089. [本文引用:1]
[29] Zhang W, Wu B H, Sun S T, et al. Nature Communications, 2021, 12: 4082. [本文引用:1]