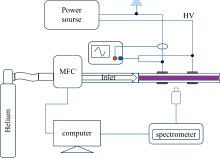
实验装置如图1所示, 包括等离子体发生系统、 光谱诊断系统、 电学参量诊断系统三部分。 其中等离子体发生系统为环-环电极结构, 两环电极采用厚1.0 mm宽5.0 mm铝环电极, 间距10.0 mm, 包覆在内径1.0 mm外径2.3 mm的石英管上, 近管口铝环电极与低温等离子体电源(CTP-2000K)高压端相连, 另一铝环电极接地。 电源输出电压调节范围为0~30 kV, 放电频率为18.5 kHz, 放电电压、 电流通过高压探头(P6015A)和电流探头(P2877)测量, 在数字示波器(UTD2102CEX-II)上记录。 工作气体选用氦气(纯度99.999%), 经计算机连接质量流量控制器(CS200A)控制氦流量, 等离子体发射光谱由光纤光谱仪(AvaSpec-ULS4096CL-EVO)测量, 光纤探头固定在与等离子体中心轴向的垂直间距为10.0 mm的位置。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 等离子体发生和诊断系统Fig.1 Plasma generators and diagnostic systems

发射光谱法通过采集等离子体自发辐射的光信号进行分析, 无需引入外部探针或采样装置, 避免了传统电探针可能引发的等离子体扰动(如鞘层效应、 粒子复合), 光谱范围200~900 nm, 兼顾原子、 分子和离子谱线检测, 具备多参数同步诊断能力, 是一种使用范围极广、 测量结果准确的非侵入式等离子体诊断方法^{[16, 17]}。

1.2.1 玻尔兹曼斜率法测算电子激发温度

局部热力学平衡(LTE)条件下, 等离子体中处于不同激发态的粒子数密度遵循玻尔兹曼分布规律, 采用玻尔兹曼斜率法估算局部热平衡等离子体激发温度

lnIλgA=-EkTe+lnhcN4πZ(1)

式(1)中, I为谱线强度, g为统计权重, A为自发辐射系数, λ 为跃迁波长, E为上能级能量, k为玻尔兹曼常数, T_e为电子激发温度, h为普朗克常数, c为真空光速, Z为分配函数, 通过lnIλ /gA与E的斜率可得电子激发温度。

1.2.2 Stark展宽法测算电子密度

Stark展宽的理论基础可追溯至Griem的经典碰撞近似理论及后续的量子力学修正模型, 对氢类原子, 基于精确的Schrö dinger方程解, Stark展宽参数库已实现温度/密度全范围覆盖, 计算误差小于5%, 选择Hα 谱线对等离子体电子密度进行计算, Hα 谱线的半高全宽和等离子体电子密度之间表达式为

ne=8.02×1012Δλ1/2α1/23/2(2)

式(2)中, n_e为电子密度, Δ λ _1/2为谱线半高全宽, α _1/2为比例常数, 根据Hα 谱线洛伦兹拟合半高全宽, 可得等离子体电子密度。

控制氦气流量为0.5 SLM, 在不同输入电压下大气压氦介质阻挡放电的电流电压时序如图2所示。 随输入电压增大, 电极间电压波形整体幅值增加, 形态无明显变化, 电流波形整体幅值增加, 电流波形在不同电压区间呈现显著差异。 根据电流脉冲个数的不同, 若每个外加电压半周期内存在1或几个持续时间长(约微秒级)的电流脉冲, 且脉冲在数个周期内出现在相同位置, 则为均匀放电。 若在半周期内存在一系列持续时间短(约纳秒级)强度较大的电流脉冲, 则为丝状放电^{[18, 19, 20]}。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 不同输入电压下的电流-电压波形Fig.2 The current and voltage waveform at different discharge voltages

实验结果表明, 在低电压区间(9~11 kV)呈典型的均匀放电模式, 其电流脉冲在上升、 下降沿呈现约1 μ s的对称展宽现象; 在中电压区间(11~15 kV)表现出放电模式转变, “ 下降沿” 仍保持微秒量级脉冲宽度, 而“ 上升沿” 出现一系列亚微秒级电流脉冲, 形成非对称丝状放电模式; 在高电压区间(15~18 kV), 上升、 下降沿均出现高密度亚微秒级电流脉冲群, 呈对称性丝状放电模式。

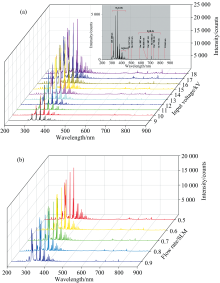
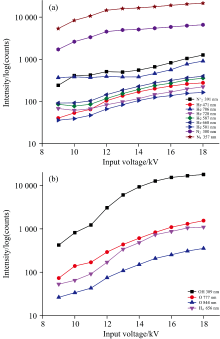
氦APDBD等离子体发射光子体发射光谱如图3所示, 图3(a)为控制氦气流量0.5 SLM、 在不同输入电压下的光谱, 图3(b)为输入电压15 kV、 在不同氦气流量下的光谱; 其中主要包括氮分子的激发态N₂(C-B)和N₂(B-A)、 氮分子离子 N2+(B-X)、 氧原子O I的2条谱线和氦原子He I的6条谱线, 这是高能电子和氮分子、 氧分子、 氦原子经电子碰撞引起电离、 激发反应和重粒子间的碰撞反应产生; 另外, 谱图中还明显存在羟基OH(A-X)发射谱线和氢原子H_α 谱线, 说明在大气环境中放电存有少量H₂O掺杂。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同工况下氦等离子体发射光谱Fig.3 Helium plasma emission spectra under different operating conditions

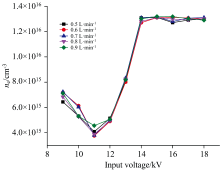
当输入电压在9~18 kV范围, 氦APDBD等离子体电子密度呈现“ 下降-上升-饱和” 三个阶段特征, 如图4所示。 控制氦气流量为0.5 SLM, 当输入电压在9~11 kV范围, 电子密度随输入电压上升而逐渐下降, 由6.43× 10¹⁵ cm^-3降至4.08× 10¹⁵ cm^-3, 降幅达36%, 主要归因于在均匀放电模式下电子-离子复合速率优势超过电离速率, 同时介质表面电荷积累导致的反向电场进一步抑制电离过程。 当输入电压升至11~15 kV时, 由4.08× 10¹⁵ cm^-3增至1.31× 10¹⁶ cm^-3, 增幅达221%, 在非对称丝状放电模式下的电离速率因局部电场强度与放电丝数量的双重增加而显著提升, 电子密度呈指数增长。 当输入电压升至15~18 kV时, 电子密度进入动态平衡状态: 电离速率与复合速率因电子密度升高达到平衡。 在控制氦气流量在0.5~0.9 SLM范围内, 电子密度无明显差异, 和Xu^[21]等采用二维流体模型进行数值模拟的方法所得结论一致, 随氦气流量增大时, 等离子体电离速率和复合速率保持相对平衡, 流量增加使气体流速加快, 导致电子和离子在放电区域的停留时间缩短, 复合速率降低, 但气体流量增加同时使得电子激发温度降低, 电离速度从而降低, 这两方面因素相互平衡, 使得电子密度无显著变化。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同工况下电子密度Fig.4 The electron density under different operating conditions

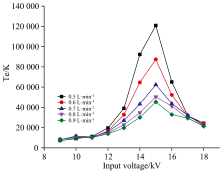
通过玻尔兹曼斜率法选取He I 在波长为471、 706和728 nm三条激发能级差较大的谱线计算不同放电条件下氦APDBD等离子体电子激发温度, 如图5所示。 电子激发温度的演化呈现明显的区间依赖性: 控制氦气流量为0.5 SLM, 在9~11 kV输入电压范围内缓慢上升, 由7 157 K 增至11 163 K, 增幅为56%, 在11~15 kV输入电压范围内快速升高, 由11 163 K增至120 879 K, 增幅高达983%, 在15~18 kV输入电压范围内则急剧下降, 由120 879 K 降至24 335 K, 降幅为79%。 在输入电压较低范围(9~11 kV)的缓慢升温源于均匀电场中电子的有限加速能力即电场增强, 可提升电子平均能量, 但均匀放电的宽空间分布导致电子-分子碰撞频率过高, 能量弛豫速率加快, 抑制高能电子比例的显著增长。 在11~15 kV输入电压范围内, 微放电丝内的强局部电场使电子自由程延长, 加速时间增加, 电子动能呈现超线性增长, 激发温度迅速升高。 当输入电压超过15 kV, 放电丝密度饱和导致单位通道的电场强度分散, 叠加高电子密度引发的空间电荷屏蔽效应, 净电场强度大幅降低, 电子加速效率下降, 激发温度回落。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同工况下电子激发温度Fig.5 The electron excitation temperature under different operating conditions

在非对称丝状放电和对称丝状放电模式、 相同输入电压下, 电子激发温度随氦气流量提升而降低, 主要归因于气体流动的冷却作用和电子-中性粒子碰撞频率增加两方面: 一方面, 氦气流量提升、 气体流速加快, 单位时间内从放电区域带走的热量增加, 导致等离子体整体温度下降; 另一方面, 氦气流量提升, 电子与中性氦原子的碰撞频率随之增加, 导致电子在加速过程中与中性粒子的能量交换更频繁, 高能电子通过非弹性碰撞将能量转移给中性粒子, 自身能量耗散加剧, 从而抑制激发温度上升。

控制氦气流量为0.5 SLM, 谱线强度随输入电压变化情况如图6所示。 显示氦APDBD等离子体中主要活性粒子谱线强度随输入电压的增加而增加, 且谱线强度变化在不同放电模式下存在显著差异。 在9~11 kV输入电压范围的均匀放电模式, 活性粒子(氧原子谱线和氦原子谱线)主要通过低能电子的激发与潘宁电离产生, 受限于电子密度与能量分布的稳定性, 其浓度增长缓慢。 当输入电压进入11~15 kV范围的非对称丝状放电模式时, 微放电丝内局部电场强度剧增, 电子能量显著提升, 总产率随放电丝密度增加而迅速增加。 到15~18 kV的对称丝状放电阶段, 尽管单丝通道内电子激发温度下降, 但放电丝总数量的增加导致活性粒子整体浓度仍持续上升。 而亚稳态氦原子潘宁电离效应对氮分子激发态N₂、 氮分子离子 N2+的生成速率具有放大效应, 在均匀放电模式, 氮物种产率随输入电压提升而增大。 在非对称丝状放电模式, 由于氮气为杂质气体, 即使亚稳态氦原子的密度增加, 氮物种产率受反应物浓度限制而趋于稳定。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 氦APDBD等离子体特征谱线相对强度随输入电压变化情况Fig.6 Variation of relative intensity of helium APDBD characteristic plasma with the input voltage

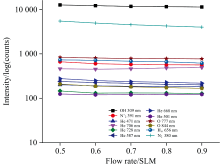
控制输入电压为15 kV, 谱线强度随氦气流量变化情况如图7所示, 氦APDBD等离子体中主要活性粒子谱线强度随氦气流量提升而变化幅度不大, 除He I在706 nm处的特征谱线相对强度提升6.99%外, 其余活性粒子谱线强度均呈现下降趋势, 其中以选取的N₂ 380 nm、 He 668 nm和O 844 nm处的特征谱线相对强度降幅较大, 分别为27.02%、21.18%和19.53%。 此现象可归因: 随氦气流量提升, 电子激发温度降低, 从而导致高能级激发态产率下降, 而He 706 nm的谱线对应跃迁的激发能相对其余He原子谱线所需电子能量较低, 低能电子仍能有效激发该跃迁行为, 而更高能级的激发效率显著降低, 导致仅He 706 nm谱线强度上升, 而其他谱线强度下降。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 氦APDBD等离子体特征谱线相对强度随氦气流量变化情况Fig.7 Variation of relative intensity of helium APDBD characteristic plasma with the Flow rate