基于WPS-GMM的土壤XRF光谱重叠峰解析方法研究

引用本文

李唐虎, 甘婷婷, 赵南京, 殷高方, 汪颖, 李星池, 盛若愚, 叶紫琪. 基于WPS-GMM的土壤XRF光谱重叠峰解析方法研究[J]. 光谱学与光谱分析, 2025,45(10): 2737-2746.
LI Tang-hu, GAN Ting-ting, ZHAO Nan-jing, YIN Gao-fang, WANG Ying, LI Xing-chi, SHENG Ruo-yu, YE Zi-qi. Resolution Method of Overlapping Peaks in Soil XRF Spectrum Based on WPS-GMM[J]. Spectroscopy and Spectral Analysis, 2025,45(10): 2737-2746.
Doi:10.3964/j.issn.1000-0593(2025)10-2737-10 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于WPS-GMM的土壤XRF光谱重叠峰解析方法研究

李唐虎², 甘婷婷^1,^4,^*, 赵南京^1,^2,^3,^4,^5,^*, 殷高方^1,^4,⁵, 汪颖^1,^3,⁴, 李星池^1,^3,⁴, 盛若愚^1,^3,⁴, 叶紫琪^1,^3,⁴

1. 中国科学院合肥物质科学研究院安徽光学精密机械研究所, 中国科学院环境光学与技术重点实验室, 安徽合肥 230031

2. 安徽大学物质科学与信息技术研究院, 安徽合肥 230601

3. 中国科学技术大学, 安徽合肥 230026

4. 安徽省环境光学监测技术重点实验室, 安徽合肥 230031

5. 合肥综合性国家科学中心环境研究院, 安徽合肥 230031

*通讯作者 e-mail: ttgan@aiofm.ac.cn; njzhao@aiofm.ac.cn

作者简介: 李唐虎, 1998年生,安徽大学物质科学与信息技术研究院硕士研究生 e-mail: litanghu611@163.com

收稿日期: 2025-04-17 修回日期: 2025-07-31

基金: 国家重点研发计划课题(2022YFC3700804),国家自然科学基金项目(61805254)资助

摘要

X射线荧光(XRF)光谱法作为重金属现场快速检测的重要技术, 当用于土壤重金属检测时, 由于土壤所含元素较多, XRF光谱中存在部分元素特征谱峰交叉重叠问题, 影响重金属特征谱峰提取及定量分析准确性。针对该问题, 提出一种基于小波峰锐化-高斯混合模型(WPS-GMM)的土壤XRF光谱重叠峰解析方法。该方法通过离散小波变换对重叠峰进行峰锐化, 以增强信号中的重要局部特征, 明确子峰峰位, 并以其作为先验约束条件, 对重叠峰构建高斯混合模型, 进一步通过最大化似然估计模型参数, 获得重叠峰中各子峰中心峰位、积分面积等相关信息, 实现重叠峰的解析。将所建WPS-GMM方法用于土壤XRF光谱中Ni Kα-Co Kβ、 Cu Kα-Ni Kβ、 Zn Kα-Cu Kβ三组典型重叠峰解析及重叠峰中主峰对应重金属Ni、 Cu、 Zn的定量分析, 并将结果与传统仅基于高斯混合模型(GMM)的重叠峰解析方法对比, 验证所建方法的准确性。结果表明: 与GMM方法相比, 所建WPS-GMM方法对土壤XRF光谱三组重叠峰中Ni Kα、 Ni Kβ、 Cu Kα、 Cu Kβ和Zn Kα子峰峰位解析的准确率平均分别提高了77.55%、 47.03%、 52.65%、 22.07%和8.43%, 积分面积解析准确率平均分别提高了74.05%、 80.17%、 61.62%、 28.29%和43.59%; 用于Ni、 Cu、 Zn定量分析的准确率平均分别提高了73.23%、 68.47%、 47.62%; 并且用于工业用土、农用土、建筑用土三种不同用途土壤中Ni、 Cu、 Zn 准确定量分析均具有更好的普适性。因此所建WPS-GMM方法能够更准确获取不同土壤XRF光谱中重叠峰的子峰信息, 更有利于提高土壤重金属XRF定量分析准确性。该研究为土壤重金属XRF现场快速准确检测提供了重要的方法基础。

关键词: X射线荧光; 重叠峰解析; 重金属检测; 土壤; 光谱分析

中图分类号:O433.4 文献标志码:A

Resolution Method of Overlapping Peaks in Soil XRF Spectrum Based on WPS-GMM

LI Tang-hu², GAN Ting-ting^1,^4,^*, ZHAO Nan-jing^1,^2,^3,^4,^5,^*, YIN Gao-fang^1,^4,⁵, WANG Ying^1,^3,⁴, LI Xing-chi^1,^3,⁴, SHENG Ruo-yu^1,^3,⁴, YE Zi-qi^1,^3,⁴

1. Key Laboratory of Environmental Optics and Technology, Anhui Institute of Optics and Fine Mechanics, Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031, China

2. Institute of Physical Science and Information Technology, Anhui University, Hefei 230601, China

3. University of Science and Technology of China, Hefei 230026, China

4. Key Laboratory of Optical Monitoring Technology for the Environment of Anhui Province, Hefei 230031, China

5. Institute of Environment Hefei Comprehensive National Science Center, Hefei 230031, China

*Corresponding authors

Abstract

X-ray fluorescence (XRF) spectroscopy is an important technique for rapid and on-site detection of heavy metals. However, when it is used for detecting heavy metals in soil, due to the variety of elements contained in soil, there are some overlapping peaks in the soil XRF spectrum, which affects the accuracy of characteristic peak extraction and quantitative analysis of heavy metals. For this problem, this paper proposed a method for resolving the overlapping peaks in soil XRF spectra based on wavelet peak sharpening and Gaussian mixture model (WPS-GMM). This method first sharpened the overlapping peaks by a discrete wavelet transform to enhance the important local features of the spectral signal and clarify the peak positions of subpeaks. Then, using it as a prior constraint, a Gaussian mixture model of the overlapping peak was constructed. Finally, the relevant information for each subpeak in the overlapping peak was obtained by maximizing the likelihood to estimate the model parameters, thereby achieving the resolution of the overlapping peak. The established WPS-GMM method was applied to the resolution of typical overlapping peaks of Ni Kα-Co Kβ, Cu Kα-Ni Kβ, and Zn Kα-Cu Kβ in soil XRF spectra, as well as the quantitative analysis of Ni, Cu, and Zn corresponding to the main peaks in the overlapping peaks, to verify it saccuracy by comparing with the traditional resolution method for overlapping peaks based solely on the Gaussian mixture model (GMM). The results showed that compared with the GMM method, when the established WPS-GMM method was used for resolving the three overlapping peaks in soil XRF spectra, for the sub peaks of Ni Kα, Ni Kβ, Cu Kα, Cu Kβ and Zn Kα, the accuracy of resolved peak position increased by an average of 77.55%, 47.03%, 52.65%, 22.07%, and 8.43%, respectively, and the accuracy of resolved integral area increased by an average of 74.05%, 80.17%, 61.62%, 28.29%, and 43.59%, respectively; Moreover, the accuracy of quantitative analysis of Ni, Cu and Zn increased by an average of 73.23%, 68.47% and 47.62%, respectively. The established method demonstrated better universality for the accurate quantitative analysis of Ni, Cu, and Zn in soils with three different uses, including industrial, agricultural, and construction, by resolving the overlapping peaks in XRF spectra. Therefore, the established WPS-GMM method can more accurately obtain sub-peak information of overlapping peaks in XRF spectra of different soils, which is more conducive to improving the accuracy of quantitative analysis of heavy metals in soils by XRF. This study will provide an important methodological foundation for the rapid and accurate on-site detection of heavy metals in soil using XRF spectroscopy.

Keyword: X-ray fluorescence; Resolution of overlapping peak; Heavy metal detection; Soil; Spectral analysis

文章图片

引言

随着社会经济及工农业的快速发展, 人类活动排放的重金属在土壤中不断累积, 导致当前土壤重金属污染问题日益严峻。如我国现有34.9%的工业废弃场地及33.4%的采矿区均存在严重的土壤重金属污染^{[1, 2]}; 我国西南、湖南、浙江、海南等地的农用地也面临Cd、 Hg和Pb等超标风险^{[3, 4]}。重金属由于具有难降解性、生物富集性和生物毒性^[5], 一旦在土壤中累积, 将对生态系统功能、粮食安全和人类健康构成严重影响。因此, 实现土壤重金属现场快速检测对防治土壤重金属污染、保护生态系统安全、促进农业发展、维护人类健康具有重要作用与意义。

目前, 土壤重金属检测仍以石墨炉原子吸收光谱法^[6]、电感耦合等离子体质谱法^[7]、原子荧光光谱法^[8]为主, 这些方法虽然灵敏度高、准确性好, 但均需现场采样后再到实验室离线分析, 且样品前处理复杂、检测速度慢、分析时间长, 无法实现土壤重金属污染现场快速检测与筛查。与之相比, X射线荧光(XRF)光谱法^[9]具有对样品无破坏性、无需复杂前处理、仪器简单、操作方便、分析速度快、多种元素可同步检测等优点, 已成为重金属现场快速检测的重要技术, 在地质勘查^[10]、工业制造^[11]、资源调查^[12]、环境监测^[13]等领域具有广泛应用。但当该方法用于土壤重金属检测时, 由于土壤基质复杂, 含有大量金属元素(如Fe、 Ca、 Mg、 K、 V等)、非金属元素(如Si、 P等)及稀土元素(如Rb、 Sr、 Y、 Nb等)^{[14, 15, 16]}, 加之多种重金属往往同时共存, 且部分元素特征谱峰较为接近, 土壤XRF光谱中存在元素间谱峰交叉重叠问题, 从而影响重金属特征谱峰提取及定量分析准确性。因此, 重叠峰解析是土壤重金属XRF准确检测的关键与前提。

近年来, 国内外相关学者虽然在光谱重叠峰解析方面开展了一定的研究工作, 如: 闫晓雪等提出将粒子群算法用于γ 能谱重叠峰解析^[17]; 陈颖团队建立了基于麻雀搜索算法的XRF光谱重叠峰解析方法^[18]。但现有方法仍存在准确度不高、运算复杂、易陷入局部最优解等问题。由于XRF光谱中元素特征峰具有高斯分布特性, 基于此近年来高斯混合模型(Gaussian mixture model, GMM)已被广泛用于XRF光谱的重叠峰解析^{[18, 19]}。但采用GMM直接对XRF光谱中重叠峰进行全局建模, 由于缺乏对隐含子峰物理特征的有效约束, 易导致子峰数量误判、峰位定位偏差较大、面积权重计算失真等问题。

针对上述问题, 本文提出采用小波峰锐化法(wavelet peak sharpening, WPS)明确重叠峰中的子峰峰位信息, 以此作为约束条件建立高斯混合模型解析重叠峰, 以提高子峰特征信息解析的准确性, 从而建立一种基于小波峰锐化-高斯混合模型(WPS-GMM)的土壤XRF光谱重叠峰解析方法。并将该方法用于土壤中Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 典型重叠峰的解析及Ni、 Cu、 Zn的定量分析, 通过与GMM方法对比, 验证所建方法的准确性, 以为土壤重金属污染XRF现场快速准确检测与筛查提供方法基础。

1 WPS-GMM重叠峰解析方法及原理

1.1 基于小波变换的重叠谱峰峰锐化

小波变换能够将信号分解为不同尺度上的局部特征, 通过调节小波函数的伸缩和平移能够捕捉信号中的特征点。基于该特性, 利用小波多尺度分解提取原始重叠峰的高频残差成分, 并将其放大后与原始信号加权叠加, 即可增强重叠峰中子峰的峰位特征, 实现重叠谱峰峰锐化。

针对长度为N的土壤XRF光谱中的重叠峰信号y(t), 其离散小波变换如式(1)所示:

$W (a, b) = \overset{N - 1}{\sum_{t = 0}} y (t) Ψ_{a, b} (t)$ (1)

式(1)中, a为尺度因子, 控制小波函数的伸缩程度, b为平移因子, 决定小波函数的时间偏移量, Ψ _a_,_b(t)为母小波函数经尺度和平移变换后的基函数。采用小波变换对土壤XRF光谱中重叠峰进行峰锐化的具体步骤如下:

(1)多层小波分解: 根据式(2)对XRF光谱信号y(t)进行n层小波分解, 逐层提取高频细节系数D_i与低频近似系数A_n;

$y (t) = \overset{n}{\sum_{i = 1}} D_{i} (t) + A_{n} (t)$ (2)

(2)低频信号重构: 根据式(3)使用近似系数A_n重构信号 $\hat{y}$ (t), 该重构信号主要保留了信号的低频成分;

$\hat{y} (t) = \sum_{k} A_{n, k} \cdot ϕ_{n, k} (t)$ (3)

式(3)中, ϕ _n_,_k(t)为第n层缩放函数, k为信号中第k个信号值。

(3)计算残差信号: 根据式(4)计算原信号y(t)与重构信号 $\hat{y}$ (t)间的差值, 提取光谱信号的高频残差成分res(t);

$res (t) = y (t) - \hat{y} (t)$ (4)

(4)峰锐化处理: 根据式(5)将残差信号res(t)放大α 倍后与原信号y(t)叠加, 获得经过峰锐化后的光谱信号result(t), 达到增强子峰峰位特征的目的。

$result (t) = y (t) - α \cdot res (t)$ (5)

式(5)中, α 值越大, 重叠峰的锐化程度越大, 子峰峰位定位越准确。

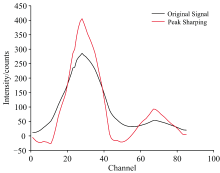
采用上述小波变换法对XRF光谱中重叠峰进行分解与重构后, 获得的光谱信息如图1所示, 可以看出, 原始XRF光谱信号和小波重构信号之差所形成的残差信号峰谷位置与原信号谱峰位置相一致。根据式(5)将原始信号与残差信号加权叠加, 结果如图2所示, 可以看出原始XRF光谱重叠峰实现了峰锐化, 通过峰锐化获得子峰具体位置后将更有利于后续重叠峰的准确解析。

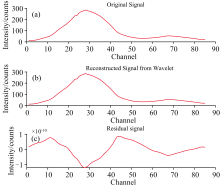	Figure Option View Download New Window
	图1 原始重叠峰信号经离散小波变换后获得的重构信号与残差信号Fig.1 Reconstructed signal and residual signal of the original overlapping peak signal after discrete wavelet transform

	Figure Option View Download New Window
	图2 峰锐化前后重叠谱峰对比图Fig.2 Comparison of overlapping spectral peaks before and after peak sharpening

1.2 重叠峰高斯混合模型的构建

高斯混合模型是一种基于概率密度估计的统计模型, 适用于对多模态分布数据的建模与分析。根据XRF产生的物理机制, XRF光谱中元素特征谱峰具有高斯分布特性, 高斯函数是表征元素单一特征峰中X射线光量子随能量统计分布最为适用的方法。对于XRF光谱中不同元素特征谱峰中心能量接近而在能量轴上发生空间交叠所形成的重叠峰, 由于其由多个高斯分布特征峰叠加而成, 因此利用重叠峰中各子峰所具有的高斯分布特性, 通过建立高斯混合模型解析重叠峰, 能够提高对XRF重叠峰描述的准确性。

高斯混合模型所表达的概率密度函数p(x)如式(6)所示

$p (x) = \overset{K}{\sum_{k = 1}} π_{k} N (x| μ_{k}, σ_{k}^{2})$ (6)

式(6)中, 单高斯分布函数N(x│μ _k, $σ_{k}^{2}$ )表达式如式(7)所示

$N (x│ μ_{k}, σ_{k}^{2}) = \frac{1}{\sqrt[]{2 π σ_{k}^{2}}} \exp (- \frac{(x - μ_{k})^{2}}{2 σ_{k}^{2}})$ (7)

式(7)中, K为模型中高斯分布的子峰个数; π _k为第k个高斯分布子峰所占的权重, 满足 $\overset{K}{\sum_{k = 1}} π_{k} = 1$ ; $μ_{k}$ 为第 $k$ 个子峰的均值, 对应谱峰中心峰位; $σ_{k}^{2}$ 为第 $k$ 个子峰的方差, 反映峰宽信息。采用高斯混合模型进行重叠峰解析的具体步骤如下:

(1)光谱预处理: 对重叠峰信号去噪并进行基线校正, 获得扣除背景后平滑的净重叠谱峰信号;

(2)初始化参数: 设定模型的初始化参数, 包括成分数量 $K$ 、均值 $μ_{k}$ 、方差 ${σ_{k}}^{2}$ 和权重 $π_{k};$

(3)期望最大化(expectation maximum, EM)算法确定模型最优参数: 通过EM算法迭代过程不断交替进行E步和M步, 直到模型参数收敛, 以获得子峰的均值、方差和权重等参数, 实现重叠峰的分离。该步骤包括E步和M步:

①期望步骤(E步): 基于当前的模型参数估计潜在变量的后验分布, 具体如式(8)所示。

$γ_{ik} = \frac{π_{k} N (x_{i} │ μ_{k}, σ_{k}^{2})}{\overset{K}{\sum_{j = 1}} π_{j} N (x_{i} │ μ_{j}, σ_{j}^{2})}$ (8)

式(8)中, γ _ik是样本点x_i属于第k个高斯成分的概率。

②最大化步骤(M步): 利用在E步中得到的潜在变量的估计值, 通过设置偏导数为零或采用数值优化方法, 更新模型参数, 使得对数似然函数最大化, 以获得最佳的模型参数, 具体如式(9)— 式(11)所示。

均值更新

$μ_{k}^{new} = \frac{\overset{N}{\sum_{i = 1}} γ_{ik} x_{i}}{\overset{N}{\sum_{i = 1}} γ_{ik}}$ (9)

方差更新

$(σ_{k}^{2})^{new} = \frac{\overset{N}{\sum_{i = 1}} γ_{ik} (x_{i} - μ_{k})^{2}}{\overset{N}{\sum_{i = 1}} γ_{ik}}$ (10)

权重更新

$π_{k}^{new} = \frac{1}{N} \overset{N}{\sum_{i = 1}} γ_{ik}$ (11)

1.3 基于WPS-GMM方法的土壤XRF光谱重叠峰解析流程

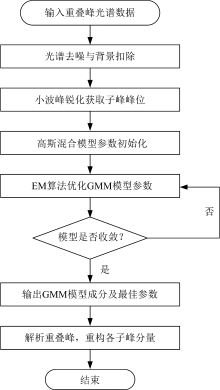
将小波峰锐化与高斯混合模型相结合所建立的基于WPS-GMM的土壤XRF光谱重叠峰解析方法具体流程如图3 所示:

	Figure Option View Download New Window
	图3 基于WPS-GMM的重叠峰解析方法流程图Fig.3 Flowchart of overlapping peak resolution method based on WPS-GMM

(1)输入重叠峰XRF光谱信号;

(2)基于小波阈值去噪结合非线性迭代剥峰算法, 对原始重叠峰光谱进行平滑去噪与背景扣除, 获得净重叠峰光谱数据;

(3)采用sym4小波基函数对净重叠峰光谱信号进行4层分解与重构, 获取原信号与重构信号之间的差值, 将差值信号放大后与原信号叠加, 实现重叠谱峰的峰锐化, 获取子峰的峰位信息;

(4)根据净重叠峰光谱数据构建高斯混合模型并设置初始化参数: 包括子峰数量K、均值μ _k、方差 $σ_{k}^{2}$ 和权重π _k;

(5)执行期望最大化(EM)算法进行参数估计: 迭代进行E步和M步, 直到模型参数收敛, 以实现重叠峰中子峰成分解析, 获得子峰的均值、方差和权重等参数。

(6)基于模型参数重构各高斯子峰分量, 实现重叠峰分解。

2 实验部分

2.1 样品制备

镍(Ni)、铜(Cu)、锌(Zn)、钴(Co)作为典型重金属污染物, 在重金属复合污染土壤中往往同时存在, 但由于Ni Kα (7.47 keV)与Co Kβ (7.65 keV)、 Cu Kα (8.04 keV)与Ni Kβ (8.27 keV)、 Zn Kα (8.63 keV)与Cu Kβ (8.91 keV)特征谱峰能量极为接近, 彼此交叉重叠, 是土壤XRF光谱中典型重叠峰, 因此本研究以Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠峰为研究对象, 验证所建WPS-GMM方法的解析性能。

为了避免土壤中其他元素因吸收增强效应对上述4种重金属特征谱峰强度产生干扰而影响方法性能验证, 且考虑土壤中主要成分为SiO₂, 本研究以SiO₂模拟土样基质, 通过向其中加入不同体积的1 000 mg· L^-1 Ni、 Co、 Cu、 Zn单元素储备液, 经混匀、烘干、研磨后, 取3 g于8 MPa压力下保压3 min, 分别制成Co、 Ni、 Cu、 Zn共存且含量不同的6个圆片形土壤样品, 以及与这6个土壤样品中重金属含量相同的24个单一元素(6个Ni、 6个Co、 6个Cu、 6个Zn)圆片形土壤样品, 用于验证WPS-GMM重叠峰解析方法的准确性, 每个样品厚度为2 mm、直径为30 mm。其中, Co、 Ni、 Cu、 Zn共存的6个土壤样品经iCAP RQ型电感耦合等离子体-质谱仪(ICP-MS, Thermo Fisher Scientific, 美国)测量所获得的四种元素真实含量如表1所示。

表1 四种重金属共存的6个样品中重金属含量值(mg· kg^-1) Table 1 Heavy metal contents of 6 samples with coexistence of four heavy metals (mg· kg^-1)

以分别采自于天津北辰工业区的工业用土、武汉市洪山区某建筑工程场地的建筑用土、合肥市科学岛的农用土为研究对象, 通过向其中分别加入不同量的1 000 mg· L^-1 Ni、 Co、 Cu、 Zn单元素储备液, 经混匀、烘干、研磨、过100目筛, 采用与上述同样方法分别制成Ni、 Co、 Cu、 Zn共存且含量不同的三种用途圆片形土壤样品, 用于验证所建WPS-GMM方法的普适性。

2.2 XRF光谱测量

XRF光谱测量所用仪器为Amptek公司的能量色散XRF光谱分析仪, 激发源为Mini-X型X射线管, 靶材为Ag靶, 并配有500 μ m Al滤光片, 探测器为X123-SDD型硅漂移探测器。 XRF光谱测量相关参数设置为: 激发电流20 μ A、激发电压40 kV、脉冲整形峰值时间及宽度分别为6.4和0.8 μ s、增益47.47、信号累积时间2 min。

2.3 WPS-GMM方法准确性验证

分别采用WPS-GMM方法与GMM方法进行重叠峰解析后, 将获得的子峰信息(W_a)与子峰真实信息(W_r)进行比对, 根据式(12)获取子峰信息的相对误差(RE), 通过将WPS-GMM方法解析结果的RE与GMM方法解析结果的RE对比, 验证WPS-GMM方法的准确性。进一步将WPS-GMM方法与GMM方法解析后的谱峰积分面积用于重金属定量分析, 同样根据式(12)获取重金属含量反演结果的RE, 将WPS-GMM方法与GMM方法对比, 验证WPS-GMM方法在重金属定量分析中的准确性。

$RE = |\frac{W_{a} - W_{r}}{W_{r}}| \times 100 %$ (12)

3 结果与讨论

3.1 重叠谱峰解析准确性

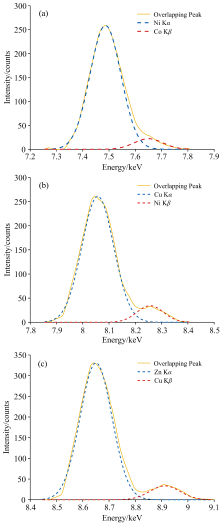
表1中不同含量Ni、 Co、 Cu、 Zn共存的6个土壤样品XRF光谱中Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组典型重叠峰如图4所示, 采用WPS-GMM方法对图4中6个土壤样品的Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠峰进行解析, 其中含有489.80 mg· L^-1 Co、 405.13 mg· L^-1 Ni、 399.69 mg· L^-1 Cu、 551.75 mg· L^-1 Zn样品所获得的各子峰的分布特征如图5所示。

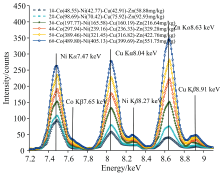	Figure Option View Download New Window
	图4 Ni、 Co、 Cu、 Zn共存土壤XRF光谱中三组典型重叠峰Fig.4 Three typical overlapping peaks in XRF spectra of Ni, Co, Cu, and Zn coexisting soils

	Figure Option View Download New Window
	图5 三组典型重叠峰解析效果图Fig.5 Resolution effect diagram of three typical overlapping peaks

将WPS-GMM方法与传统GMM方法对图4中不同样品三组重叠峰的解析结果分别与Ni、 Co、 Cu、 Zn单元素样品相应特征谱峰信息进行对比, 分别从子峰峰位及积分面积两个方面验证所建WPS-GMM方法的准确性。但由于受周围环境影响, 所测得的Co单元素样品XRF光谱中其Kβ 特征谱峰始终有其他谱峰干扰, 无法准确获取Co Kβ 特征谱峰的真实信息, 因此仅以三组重叠峰中Ni Kα 、 Ni Kβ 、 Cu Kα 、 Cu Kβ 、 Zn Kα 五个子峰验证所建方法的准确性。

3.1.1 子峰峰位解析准确性

GMM与WPS-GMM两种方法对图4中6个不同土壤样品Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠峰解析所获得的五个子峰峰位的相对误差及其平均值分别如图6和图7所示。可以看出, 与传统GMM方法相比, 当采用WPS-GMM方法进行重叠峰解析时, 6个样品三组重叠峰中Ni Kα 、 Ni Kβ 、 Cu Kα 、 Cu Kβ 、 Zn Kα 五个子峰中心峰位解析的相对误差大多都有所降低, 峰位平均相对误差分别由0.05%、 0.56%、 0.05%、 0.15%、 0.04%降低到了0.01%、0.30%、 0.02%、 0.11%、 0.03%, 五个子峰峰位识别准确性分别平均提高了77.55%、 47.03%、 52.65%、 22.07%和8.43%。这一结果表明, 所提出的WPS-GMM重叠峰解析方法与传统GMM方法相比, 能够更准确判定重叠峰所蕴含的不同子峰中心峰位信息, 更有利于提高重叠峰解析的准确性。

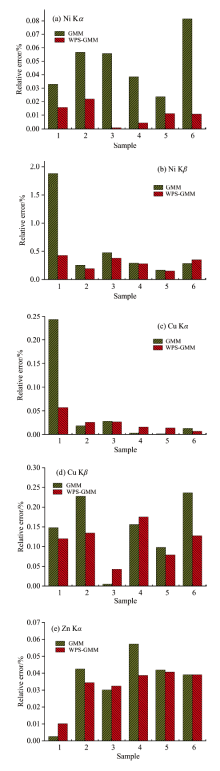	Figure Option View Download New Window
	图6 两种解析方法获得的五个子峰中心峰位的相对误差Fig.6 Relative errors of central peak positions of five sub peaks obtained by two resolution methods

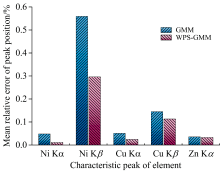	Figure Option View Download New Window
	图7 两种解析方法所获得的6个样品中各子峰峰位的平均相对误差 3.1.2 子峰积分面积解析准确性Fig.7 Average relative error of peak position of each sub peak in six samples obtained by two resolution methods

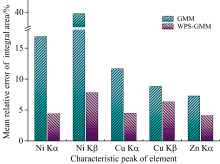
GMM与WPS-GMM两种方法对图4中6个土壤样品Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠峰解析所获得的Ni Kα 、 Ni Kβ 、 Cu Kα 、 Cu Kβ 、 Zn Kα 五个子峰积分面积的相对误差及其平均值分别如图8和图9所示。可以看出, 当采用WPS-GMM方法进行重叠峰解析时, 与GMM方法相比, 所解析出的6个样品五个子峰积分面积的相对误差大多数都有较大程度的降低, 其中Ni Kα 、 Ni Kβ 、 Cu Kα 、 Cu Kβ 、 Zn Kα 积分面积平均相对误差分别由16.86%、 39.43%、 11.67%、 8.81%、 7.26%降到了4.38%、 7.81%、 4.48%、 6.32%、 4.10%, 解析准确性分别平均提高了74.05%、 80.17%、 61.62%、 28.29%和43.59%。这一结果也表明, 相比于仅基于GMM进行重叠峰解析, 所提出的WPS-GMM方法通过小波峰锐化, 能够更准确获取重叠峰中不同子峰的积分面积信息, 因此更有利于提高重叠峰解析的准确性。

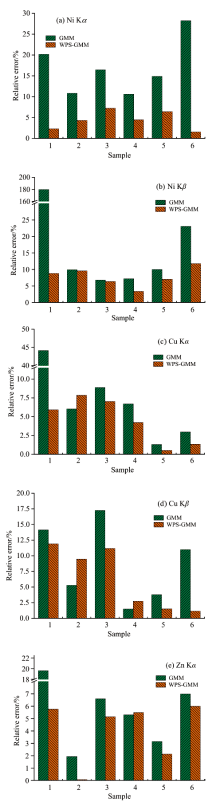	Figure Option View Download New Window
	图8 两种解析方法获得的五个子峰积分面积的相对误差Fig.8 Relative errors of integral areas of five sub peaks obtained by two resolution methods

	Figure Option View Download New Window
	图9 两种解析方法所获得的6个样品中各子峰积分面积的平均相对误差Fig.9 Average relative error of integral area of each sub peak in six samples obtained by two resolution methods

3.2 重金属定量分析准确性

重叠峰准确解析对提高重金属XRF定量检测准确性具有重要作用与意义。本研究同样以图4中Ni、 Co、 Cu、 Zn共存的土壤样品XRF光谱中Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠谱峰为研究对象, 将WPS-GMM方法与传统GMM方法解析所获得的重叠峰中三个主峰Ni Kα 、 Cu Kα 和Zn Kα 的积分面积分别带入由Ni、 Cu、 Zn单元素样品所建立的三种重金属定量分析曲线中, 以反演出四种重金属共存的土壤中Ni、 Cu、 Zn的含量值。并将不同重叠峰解析方法所获得的重金属含量值与ICP-MS所测得的真实含量值对比, 以相对误差(RE)评估两种重叠峰解析方法用于土壤重金属定量分析的准确性, 则GMM及WPS-GMM方法重叠峰解析后, 6个土壤样品中Ni、 Cu、 Zn含量的RE如表2 所示。

表2 GMM与WPS-GMM方法重叠峰解析后重金属含量反演的相对误差 Table 2 Relative errors of heavy metal contents inverted after overlapping peak resolution by GMM and WPS-GMM methods

可以看出, 与传统GMM方法相比, 当以WPS-GMM方法所解析出的Ni Kα 、 Cu Kα 和Zn Kα 三个子峰信息进行Ni、 Cu、 Zn含量反演时, 除了2#样品中的Cu及4#样品中的Zn以外, 6个样品三组重叠峰中主峰对应的三种重金属定量分析的RE均有较大程度的降低, 其中Ni含量的RE由18.36%~98.39%降到了2.68%~16.78%, Cu含量的RE由1.47%~108.90%降到了0.52%~14.69%, Zn含量的RE由3.42%~23.61%降到了1.11%~6.41%; 总体上, 6个土壤样品中Ni、 Cu、 Zn含量反演值的平均RE分别由41.58%、 24.36%、 8.42%降到了11.13%、 7.68%、 4.41%, 定量分析的准确性平均分别提高了73.23%、 68.47%、 47.62%。这一结果也表明, 所提出的WPS-GMM方法比传统GMM方法能够更有利于提高谱峰重叠情况下土壤中重金属XRF定量分析的准确性。

3.3 不同用途土壤重金属定量分析普适性

为验证本研究所提出的WPS-GMM重叠峰解析方法用于不同用途土壤中重金属准确定量分析的普适性, 选取农用土、工业用土、建筑用土三种不同用途土壤为研究对象, 分别配制具有8个浓度梯度的Co、 Ni、 Cu、 Zn共存的三组土壤样品, 每组样品中Co、 Ni、 Cu、 Zn浓度范围均为0~500 mg· kg^-1, 并采用ICP-MS标准方法测定每一样品中四种重金属的真实含量值。将每个样品XRF光谱中Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠峰分别采用GMM和WPS-GMM方法进行解析, 并根据所解析出的Ni Kα 、 Cu Kα 和Zn Kα 三个子峰积分面积与ICP-MS测得的重金属真实含量值, 建立Ni、 Cu、 Zn的定量分析曲线, 结果如表3所示, 其中三种不同用途土壤中Ni的定量分析曲线如图10所示。

表3 经GMM和WPS-GMM方法重叠峰解析后不同用途土壤中Ni、 Cu、 Zn的定量分析曲线 Table 3 Quantitative analysis curves of Ni, Cu and Zn in soils with different uses after overlapping peak resolution by GMM and WPS-GMM methods

	Figure Option View Download New Window
	图10 三种不同用途土壤中Ni的定量分析曲线(a): 农用土; (b): 工业用土; (c): 建筑用土Fig.10 Quantitative analysis curves of Ni in soils with three different uses(a): Agricultural soil; (b): Industrial soil; (c): Construction soil

由表3和图10可以看出, 对于三种不同用途土壤样品中的Ni Kα -Co Kβ 、 Cu Kα -Ni Kβ 、 Zn Kα -Cu Kβ 三组重叠峰, 经GMM方法及WPS-GMM方法解析后, 重叠峰中主峰Ni Kα 、 Cu Kα 及Zn Kα 积分面积与三种重金属真实含量间均呈线性正相关关系, 但与GMM方法相比, 经WPS-GMM方法重叠峰解析后, 三种重金属定量分析曲线均具有更好的线性拟合度, 线性相关系数(R²)均有所增加, 其中Cu元素R²由0.990 8~0.995 2增加到了0.992 2~0.996 9, Zn元素R²由0.933 6~0.993 7增加到了0.995 1~0.996 5, 而Ni元素定量分析曲线线性关系改善程度最大, R²由0.805 6~0.926 9增加到了0.973 7~0.991 5。由此可见, 相对于传统GMM重叠峰解析方法, 本研究所提出的WPS-GMM方法更适用于不同用途土壤XRF光谱中重叠谱峰的准确解析, 更有利于提高不同用途土壤中重金属XRF定量检测的准确性, 因此对不同用途土壤具有更好的普适性。

4 结论

将小波峰锐化与高斯混合模型解析方法相结合, 建立了一种基于WPS-GMM的土壤XRF光谱重叠峰解析新方法。与传统仅基于GMM的重叠峰解析方法相比, 所建WPS-GMM重叠峰解析方法能够更准确获取土壤XRF光谱中重叠峰所包含的子峰峰位、积分面积等谱峰信息, 更有利于提高土壤重金属XRF定量检测准确性, 并且在不同用途土壤重叠峰准确解析及重金属XRF准确定量分析方面具有更好的普适性, 是土壤重金属XRF现场检测应用中较为合适的多元素特征谱峰交叉重叠解析方法。所建方法为土壤重金属污染XRF现场快速准确检测与筛查提供了重要的方法基础。

参考文献

文献列表

[1]	Sun Y, Li H, Guo G, et al. Journal of Environmental Management, 2019, 251: 109512. [本文引用:1]
[2]	Wu Q, Hu W, Wang H, et al. Science of the Total Environment, 2021, 780: 146557. [本文引用:1]
[3]	Zhang Y, Li L, Song B, et al. Exposure and Health, 2025, 17: 1. [本文引用:1]
[4]	Wei A N, Jia J, Chang P Y, et al. Agronomy-Basel, 2024, 14: 450. [本文引用:1]
[5]	Wang Y K, Zhang Z, Li Y Y, et al. Journal of Hazardous Materials, 2024, 471: 134410. [本文引用:1]
[6]	Ramdani S, Amar A, Belhsaien K, et al. Analytical Letters, 2018, 51: 2468. [本文引用:1]
[7]	Shaheen M E, Tawfik W, Mankoula A F, et al. Environmental Science and Pollution Research, 2021, 28: 36039. [本文引用:1]
[8]	Ni S, Liu G, Zhao Y, et al. Sustainability, 2023, 15(2): 1143. [本文引用:1]
[9]	Bouzid K, Bataillard P, Bekiri F, et al. Environmental Monitoring and Assessment, 2025, 197: 354. [本文引用:1]
[10]	Liu Y, Zhang C, Zhang D, et al. Atomic Spectroscopy, 2022, 43: 378. [本文引用:1]
[11]	Sokolov A, Hasikova J, Pecerskis A, et al. Coatings, 2019, 9(7): 425. [本文引用:1]
[12]	Chubarov V M, Amosova A A, Finkelshtein A L. Inorganic Materials, 2020, 56: 1423. [本文引用:1]
[13]	Zhang Q L, Li F S, Yang W Q. Journal of Analytical Atomic Spectrometry, 2024, 39: 478. [本文引用:1]
[14]	Zhang J, Ning J, He Z, et al. Environmental Earth Sciences, 2024, 83: 600. [本文引用:1]
[15]	Shrestha G, Calvelo-Pereira R, Roudier P, et al. Geoderma, 2022, 409: 115649. [本文引用:1]
[16]	Temga J P, Sababa E, Mamdem L E, et al. Geoderma Regional, 2021, 25: e00369. [本文引用:1]
[17]	YAN Xiao-xue, WANG Chong-jie(闫晓雪, 王崇杰). Physics Experimentation(物理实验), 2023, 43(7): 50. [本文引用:1]
[18]	CHEN Ying, LIU Zheng-ying, XIAO Chun-yan, et al(陈颖, 刘峥莹, 肖春艳, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(7): 2175. [本文引用:2]
[19]	ZHU Dan-dan, SUN Shi-cheng, YANG Hui, et al(朱丹丹, 孙世成, 杨惠, 等). Acta Metrologica Sinica(计量学报), 2021, 42(10): 1386. [本文引用:1]

2019

0.0

... 4%的采矿区均存在严重的土壤重金属污染^[1,2] ...

2021

0.0

... 4%的采矿区均存在严重的土壤重金属污染^[1,2] ...

2025

0.0

... 我国西南、湖南、浙江、海南等地的农用地也面临Cd、 Hg和Pb等超标风险^[3,4] ...

2024

0.0

... 我国西南、湖南、浙江、海南等地的农用地也面临Cd、 Hg和Pb等超标风险^[3,4] ...

2024

0.0

... 重金属由于具有难降解性、生物富集性和生物毒性^[5], 一旦在土壤中累积, 将对生态系统功能、粮食安全和人类健康构成严重影响 ...

2018

0.0

... 目前, 土壤重金属检测仍以石墨炉原子吸收光谱法^[6]、电感耦合等离子体质谱法^[7]、原子荧光光谱法^[8]为主, 这些方法虽然灵敏度高、准确性好, 但均需现场采样后再到实验室离线分析, 且样品前处理复杂、检测速度慢、分析时间长, 无法实现土壤重金属污染现场快速检测与筛查 ...

2021

0.0

2023

0.0

2025

0.0

... 与之相比, X射线荧光(XRF)光谱法^[9]具有对样品无破坏性、无需复杂前处理、仪器简单、操作方便、分析速度快、多种元素可同步检测等优点, 已成为重金属现场快速检测的重要技术, 在地质勘查^[10]、工业制造^[11]、资源调查^[12]、环境监测^[13]等领域具有广泛应用 ...

2022

0.0

2019

0.0

2020

0.0

2024

0.0

2024

0.0

... 但当该方法用于土壤重金属检测时, 由于土壤基质复杂, 含有大量金属元素(如Fe、 Ca、 Mg、 K、 V等)、非金属元素(如Si、 P等)及稀土元素(如Rb、 Sr、 Y、 Nb等)^[14,15,16], 加之多种重金属往往同时共存, 且部分元素特征谱峰较为接近, 土壤XRF光谱中存在元素间谱峰交叉重叠问题, 从而影响重金属特征谱峰提取及定量分析准确性 ...

2022

0.0

2021

0.0

2023

0.0

... 能谱重叠峰解析^[17] ...

2021

0.0

... 陈颖团队建立了基于麻雀搜索算法的XRF光谱重叠峰解析方法^[18] ...

... 由于XRF光谱中元素特征峰具有高斯分布特性, 基于此近年来高斯混合模型(Gaussian mixture model, GMM)已被广泛用于XRF光谱的重叠峰解析^[18,19] ...

2021

0.0

... 由于XRF光谱中元素特征峰具有高斯分布特性, 基于此近年来高斯混合模型(Gaussian mixture model, GMM)已被广泛用于XRF光谱的重叠峰解析^[18,19] ...