空间外差光谱技术(spatial heterodyne spectroscopy, SHS)是一种新型超光谱分析技术, 基于其测量快速、 简单、 集成度高等特点, 以及光谱分辨率高、 测量光通量大、 无运动部件等优点, 空间外差光谱技术(SHS)已成为光谱探测及应用领域的研究热点^{[1, 2, 3, 4, 5]}。该光谱分析技术在行星表面物质探测、 国防安全、 地质勘探等方面具有非常重要的科研价值^{[6, 7, 8]}。SHS对目标信号进行探测时, 有时目标信号过于微弱易导致采集到的干涉图光强分布不均匀^[9], 甚至光学元件加工精度及仪器组装的误差也易致使干涉条纹出现倾斜或扭曲等现象, 这些因素都是SHS光谱数据误差的来源, 都会导致最终获得的目标光谱质量下降, 甚至无法有效提取目标信号^{[10, 11, 12]}。准确评估SHS光谱与干涉图的噪声水平, 校正条纹倾斜误差, 对科学研究与工程应用都具有重要的意义。

当前, 对拉曼光谱噪声成分进行评估的方法主要有噪声估计法和信噪比估计两种。然而对于空间外差干涉图像存在的暗斑噪声以及条纹倾斜等误差因素, 普通的噪声估计方法无法有效评估干涉图的各误差成分, 因此本文提出采用基于小波变换的噪声估计法进行噪声成分评估。小波变换作为一种多尺度信号分析工具, 具备多分辨率分析、 良好的局部性特征捕捉信号的瞬时变化、 在时域和频域均可有效描述信号特征以及良好的去噪效果等优良特性, 能够更准确地分析和处理图像中的噪声, 其优良的特性使其成为信号分析处理中备受关注的研究领域^{[13, 14, 15, 16]}。本文提出的采用小波变换的噪声估计法对加入不同标准差高斯噪声的钾灯干涉图数据进行噪声估计, 并对三种方法在11个噪声水平上的估计误差取平均值, 结果表明空域相关小波变换法准确度更高, 而Donoho估计法与真实值具有更好的吻合度。因此, 本文继续将此方法应用到空间外差干涉图上, 选择不同的小波基函数与分解层数对条纹倾斜不同角度的二维干涉图进行多尺度小波分解, 并对比分析干涉条纹倾斜角度与小波分解的关系。

小波变换是一种信号的时间与尺度分析方法, 可以通过伸缩和平移等运算方法, 实现对信号进行多尺度的详细分析。小波变换的特性是能在不同的频段分层地处理图像。对于一维信号f(t), 其连续小波变换定义为.

$W_{f}(a, b)=\int_{R} f(t) \overline{\varphi_{a, b}(t)} \mathrm{d} t, f \in L^{2}(R)$(1)

φa, b(t)=1aφt-ab, a> 0, b∈R(2)

式(1)和式(2)中, φ _{a, b}(t)是小波基函数, a为尺度因子, b为平移因子。当a=2ⁿ, b∈ Z时, 即对一维信号进行一维离散小波变换。一维小波变换的本质是一维信号分别经过低通滤波和高通滤波后得到信号的低频部分和高频部分的系数矩阵。

可分离的二维小波变换也是目前图像处理中常用的方法, 根据Mallat算法, 二维小波变换可以通过一系列的一维小波变换得到^{[17, 18, 19]}。对于图像f(x, y), 定义其二维离散小波变换为

Wφ(j0, m, n)=1MN∑y=1N∑x=1Mf(x, y)φj0, m, n(x, y)(3)

WΨi(j, m, n)=1MN∑y=1N∑x=1Mf(x, y)Ψj, m, ni(x, y), i∈{H, V, D}(4)

式(3)和式(4)中, M×N是输入图像的尺寸大小, j为尺度, j0为初始尺度。 φj, m, n(x, y)和 ψj, m, ni(x, y)分别是尺度函数和小波函数, H、V、D分别代表水平、垂直、对角方向。图像 f(x, y)经二维离散小波变换后会得到四幅子图像, 分别记为LL、 HL、 LH和HH。

对图1(a)的实测钾灯干涉图一级小波分解, 可以得到如图1(b)所示的图像小波分解结构图。其中, 图1(b)中左上角子图是原图像进行一级小波分解后的低频分量图像, 代表原图像的近似细节成分LL; 右上角子图是原图像水平方向的高频细节成分HL, 左下角子图是原图像垂直方向的高频细节成分LH, 右下角子图是原图像对角方向的高频细节成分HH。利用近似细节图LL继续进行下采样就可以得到原图像的二级小波分解。以此类推, 对得到的近似细节图LL不断重复进行下采样, 就可以实现更高级次的小波分解。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 图像二维小波分解结构图 (a): 钾灯原始干涉图像; (b): 钾灯干涉图一级分解结构图Fig.1 Structure of 2D wavelet decomposition of an image (a): Potassium lamp original interference image; (b): Potassium lamp interferogram primary decomposition structure

小波变换可以将原始信号分解成多个频带, 其中高频部分主要为噪声信号, 低频部分则是原始信号。通过对高频部分的噪声信号进行处理, 可以去除噪声, 从而留下原始信号中更纯粹的低频部分^[20]。同理, 利用高通滤波后高频部分系数的噪声标准差即可估计原始信号的噪声标准差, 而经高通滤波器滤波后, 噪声的方差等于原始信号中的噪声的方差乘以该滤波器响应向量模的平方。基于小波变换的噪声标准差估计方法主要有小尺度小波变换法、 空域相关小波变换法及Donoho的鲁棒估计法^{[21, 22]}。

小尺度小波变换法, 是在一个特定尺度上对原始信号进行小波变换, 得到该尺度上的小波系数。通过高通滤波后的小波系数方差与原始信号噪声方差的关系, 估算高通滤波后的高频小波系数标准差的值。

空域相关小波变换法, 是在相邻的两个尺度上对原始信号进行小波变换, 由于原始信号中非噪声部分的高频部分在各尺度上的小波系数较大, 而噪声部分的小波系数随着相应尺度的增加而迅速减小, 因此, 通过对相邻尺度小波系数进行相关运算, 可以准确识别出原始信号中非噪声部分的特征位置, 并剔除其对应的小波系数以减小干扰, 进而利用高通滤波前后噪声标准差的关系即可估计出高通滤波后小波系数标准差的值^{[23, 24]}。

Donoho的鲁棒估计法, 为了避免受到小尺度小波系数中的高频信号的干扰, 该方法采用一种算法见式(5)来估计高通滤波后信号的噪声标准差。

σ^N=med(|ωc1(n)|)0.6745(5)

式(5)中, med为中值算子, ω c₁(n)为信号的小波系数。

在无误差的钾灯仿真干涉图上分别加入标准差为0.01、 0.02、 …、 0.1的高斯噪声, 图2(a)为加入不同标准差高斯噪声的钾灯干涉图取一行的数据图, (b)是傅里叶变换后得到的钾灯光谱图。借助小波分析依据三种噪声标准差估计法对上述干涉图数据进行噪声估计, 并将三种方法处理结果与真实标准差值进行比较, 结果如图3所示, 详细参数见表1。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 噪声标准差逐级递增的钾灯(a)干涉图与(b)光谱图Fig.2 Potassium lamp (a) interferograms and (b) spectra with stepwise increasing noise standard deviation

图3

Fig.3

	Figure Option ViewDownloadNew Window
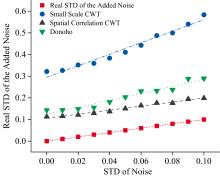	图3 三种方法估计出的噪声标准差对比图Fig.3 Comparison of the standard deviation of the noise estimated by the three methods

表1

Table 1

表1(Table 1)

表1 三种方法的相对误差平均值及与真实标准差值的线性相关性 Table 1 Mean relative errors of the three methods and linear correlation with true standard deviation values 方法 相对误差 平均值/% 线性相 关性 拟合直 线斜率 拟合直 线截距 小尺度小波变换法 37.8 0.984 9 2.658 8 0.294 9 Donoho估计法 15.5 0.974 7 1.617 6 0.123 8 空域相关小波变换法 10.2 0.989 7 0.933 8 0.105 7 真实标准差值 0 1 1 0

表1 三种方法的相对误差平均值及与真实标准差值的线性相关性 Table 1 Mean relative errors of the three methods and linear correlation with true standard deviation values

由图3与表1结果对比看出, 空域相关小波变换法估计出的噪声标准差值与真实值偏差最小, 但是Donoho估计法在修正截距后与真实值具有更好的吻合度。

由于空域相关小波变换估计法进行二维估计的算法比较繁琐, 因此本文使用Donoho估计法利用二维离散小波变换对图像进行噪声估计。如图4所示, 分别仿真三幅噪声水平不同的钾灯干涉图, 图4(a)、(b)、(c)加入的高斯噪声的标准差值分别是0、 0.03、 0.1, 选取常用的Db2小波对上述三幅仿真钾灯干涉图进行一层小波分解, 分别得到一组低频小波近似系数和三组高频小波细节系数, 用Donoho估计法估计分解一层仿真钾灯干涉图的噪声标准差, 如表2所示。通过结果对比可以明显看出噪声成分越少, 相应细节系数的标准差也越小, 仿真理想钾灯干涉图的各细节系数标准差趋近于零。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同噪声水平的仿真钾灯干涉图 (a): 仿真理想钾灯干涉图; (b): 仿真弱噪声钾灯干涉图; (c): 仿真强噪声钾灯干涉图Fig.4 Simulated potassium lamp interferogram with different noise levels (a): Simulated ideal potassium lamp interferogram; (b): Simulation of weak noise potassium lamp interferogram; (c): Simulation of strong noise potassium lamp interferogram

表2

Table 2

表2(Table 2)

表2 钾灯干涉图各细节系数标准差 Table 2 Standard deviation of each detail coefficient of potassium lamp interferogram 水平细节系 数标准差 垂直细节系 数标准差 对角细节系 数标准差 仿真理想钾灯干涉图 1.55× 10-17 0.043 7 1.51× 10-18 仿真弱噪声干涉图 0.029 7 0.046 3 0.029 9 仿真强噪声干涉图 0.093 1 0.099 4 0.092 4

表2 钾灯干涉图各细节系数标准差 Table 2 Standard deviation of each detail coefficient of potassium lamp interferogram

基于小波变换的噪声估计法不仅能在一定指标上反映出空间外差光谱的质量优劣及干涉图的噪声成分大小, 利用高级次的二维小波分解以及系数提取, 还可以有效反映由于条纹倾斜产生的数据误差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 条纹倾斜角度不同的连续光干涉图 (a): 条纹无倾斜干涉图; (b): 条纹倾斜30° 干涉图; (c): 条纹倾斜60° 干涉图Fig.5 Continuous light interferograms with different tilt angles of the stripes (a): Fringe non-tilt interferogram; (b): Fringe tilt 30° interferogram; (c): Fringe tilt 60° interferogram

不同小波函数性质各异, 所能提供的图像信息各不相同, 因此小波函数的选择对信号分析至关重要。在选择小波函数时, 必须综合考虑小波函数的正交性、 对称性、 紧支性以及消失矩阶数等一系列指标。表3列出了几种常用小波函数及其特性, 其中DbN小波和SymN小波运算量适中, 但SymN小波的对称性优于DbN小波, 并且能与原始图像保持最大的相似性。

表3

Table 3

表3(Table 3)

表3 不同小波函数的性质比较 Table 3 Properties of different wavelet function 小波函数 Coif N DbN BiorNr.Nd SymN 正交性 是 是 否 是 紧支性 是 是 是 是 对称性 近似 近似 否 近似 消失矩 2N N Nr-1 N

表3 不同小波函数的性质比较 Table 3 Properties of different wavelet function

小波的分解层数也会影响图像分解效果, 分解层数过低, 低频小波系数中仍会存在高频成分, 会影响最终的高频细节系数的噪声估计值; 而当分解层数过高时, 低频近似成分被过度分解, 致使分解图像本身发生严重失真。为了验证条纹倾斜与小波各层分解系数间存在的关联, 以一幅大小为1 024× 1 024像元的仿真连续光干涉图为原始干涉图, 从条纹倾斜角度和小波函数及分解层数的选择三个方面分别对小波分解每一层的三组高频细节系数进行分析讨论。

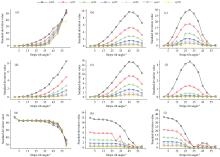
仿真过程中, 选用SymN(N=2, 3, 4, …, 8)小波分别对条纹倾斜角度为0° 、 5° 、 10° 、 …、 60° 的仿真连续干涉图进行六层分解, 通过对比分析发现, 由于水平方向细节系数图和对角方向细节系数图原始包含的图像信息少, 分解层数超过3层, 两方向的高频细节系数近乎为0且变化不明显, 无法反映随角度倾斜的变化特征, 而垂直方向细节系数包含图像信息最多, 发现在分解到第3层时垂直细节系数变化规律明显, 分解超过第3层时由于分解过度出现估值突变的情况, 因此对三个方向的变化规律需分别考虑, 水平和对角方向主要对比分解前3层, 垂直方向主要对比分解第2、 3层的变化规律。

图6为连续光干涉图分解前三层的各细节系数标准差估值对比图, (a)—(c)为对角方向, (d)—(f)为水平方向, (g)—(i)为垂直方向。研究对比发现, 三个方向的细节系数估值变化分别在分解到不同层数时呈现相似的变化规律: 细节系数估值与条纹倾斜方向和细节系数的所属方向的夹角成反比, 条纹倾斜方向与该细节系数的方向夹角越小, 估值越大, 反之则越小。图6(b)为分解第二层的对角方向细节系数估值变化图, 可以看出条纹倾斜到45° 左右时该方向细节系数估值最大, 当条纹倾斜角度超过45° 继续倾斜时, 估值逐渐减小; 图6(d)为分解第一层的水平方向细节系数估值变化图, 按照规律发展水平方向细节系数估值要在条纹倾斜到90° 左右时值最大, 如图示在条纹从0° 倾斜到60° 过程中, 水平方向细节系数估值也是逐渐增大的。图6(i)为分解第三层的垂直方向细节系数估值变化图, 可以看出垂直方向并不像水平方向变化完全呈现线性规律, 存在个别倾斜角度和分解有误的小波基函数, 但整体垂直细节系数估值变化依然符合变化规律。

图6

Fig.6

Figure Option ViewDownloadNew Window

图6 各细节系数标准差估值变化图 (a): 分解第一层的对角方向变化图; (b): 分解第二层的对角方向变化图; (c): 分解第三层的对角方向变化图; (d): 分解第一层的水平方向变化图; (e): 分解第二层的水平方向变化图; (f): 分解第三层的水平方向变化图; (g): 分解第一层的垂直方向变化图; (h): 分解第二层的垂直方向变化图; (i): 分解第三层的垂直方向变化图Fig.6 Plot of changes in standard deviation valuation of coefficients for each detail (a): Decompose the diagonal direction change map of the first layer; (b): Decomposition of the diagonal variation map of the second layer; (c): Decomposition of the diagonal direction change diagram for the third layer; (d): Decomposition of the first layer of the horizontally oriented change map; (e): Decomposition of the second layer of the horizontally oriented change map; (f): Decomposition of the horizontal orientation of the third layer of the change map; (g): Decomposition of the first layer of the vertically oriented change map; (h): Decomposition of the second layer of the vertically oriented change map; (i): Decomposition of the third layer of the vertically oriented change map

在实验过程中, 空间外差光谱仪由于目标信号微弱或者仪器组装过程出现的误差等原因导致CCD获取到的干涉图易出现条纹倾斜或扭曲等现象, 从而导致获得的目标光谱质量下降, 甚至无法有效提取信号。本文提出采用小波变换的噪声估计方法, 首先对无误差的钾灯仿真干涉图加入不同标准差的高斯噪声, 利用小波变换的噪声估计法对干涉图数据进行噪声评估, 验证基于小波变换的噪声估计法的准确性, 进而将小波分解应用于连续光干涉图的分解, 提取分解系数, 讨论干涉图条纹倾斜角度与小波分解系数的关系及变化规律。结果发现, 干涉条纹倾斜角度、 小波分解层数及小波基函数的选择均会影响小波分解高频系数标准差估值的变化, 分解得到水平、 对角与垂直三个方向的细节系数标准差估值在不同的分解层数呈现相似的变化规律, 即细节系数估值与条纹倾斜方向和细节系数的所属方向的夹角成反比, 条纹倾斜方向与该细节系数的方向夹角越小, 估值越大, 反之则越小。基于小波变换的噪声估计方法既能反映空间外差光谱、 单色光及连续光干涉图的噪声分布特性, 也能反映干涉条纹倾斜与小波分解系数间的关系。同时, 本文方法主要针对噪声在各分辨率的分布, 并不限制噪声类型, 因此可以用来评估的噪声类型不仅限于高斯噪声, 也包括常见的椒盐噪声、 斑点噪声、 泊松噪声以及均匀分布的噪声等。本研究是利用小波分解进行空间外差光谱误差分析的有益尝试, 也为后续干涉图条纹倾斜误差的校正提供了一种新途径。