光学微腔的主要参数包括Q值和模式体积。在WGM传感应用中, 具有高Q值和小模式体积的光学微腔具有更高的灵敏度。此外, 还有自由光谱范围(free spectral range, FSR)和模式线宽等谱线特征, 这些是基于光谱移动和展宽等传感技术中的重要参数。

微腔的Q值反映了其性能优劣, 其值越高, 光子寿命越长, 共振光子在腔内进行全反射的次数就越多, 模式线宽越窄。Q值与微腔的损耗有关, 包括本征损耗(Q_in)和外部损耗(Q_ext), 且有Q^-1= Qin-1+ Qext-1。本征损耗分为吸收损耗和辐射损耗, 外部损耗包括污染损耗和耦合损耗。提高微腔的品质因子还需要尽可能保证微腔的光滑度, 以减少散射损耗^[14]。

FSR是相邻波数对应的谐振波长的差值, 根据式(1), 两相邻谐振波长λ _m和λ _m+1满足模式谐振条件, 由于微腔尺寸一般远大于谐振波长, 因此可以近似得到FSR的表达式

FSR=|λm+1-λm|≈λ22πaneff(2)

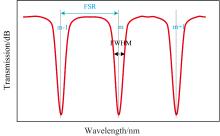
FSR与微腔尺寸和有效折射率成反比。微腔尺寸确定时, 对于相同折射率的环境, 相邻波数FSR近似相等, 如图1所示。因此, 这可以作为传感谐振峰选取的评判标准之一。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 自由光谱范围示意图Fig.1 Diagram of free spectral range

对于WGM光学微腔, 小模式体积对应高模式能量密度。在传感应用中, 需要实现模场与待测物质的增强作用以提高探测灵敏度, 因此需要微腔具有小模式体积, 这通常取决于微腔的尺寸和模式分布。

WGM传感主要利用模式漂移、 分裂和展宽三种机制来对环境变化作出快速响应, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 WGM传感机制 (a): 模式漂移; (b): 模式分裂; (c): 模式展宽Fig.2 Mechanism of WGM sensing (a): Wavelength shift; (b): Mode splitting; (c): Mode broadening

模式漂移是满足谐振条件的入射光线会在微腔内发生全反射, 当改变外界条件时, 光子的光程差发生改变, 在光谱上表现为谐振波长的蓝移或红移, 如图2(a)所示, 模式漂移反映了传感器波长随环境变化的关系, 即传感器灵敏度。

模式分裂用于检测纳米尺度的微小颗粒, 可以通过信号谱中谐振峰分裂的大小来判断对待测物的响应程度^[15]。由于WGM微腔的旋转对称性, 微腔中的行波存在正反方向传播的两种模式, 分别为顺时针和逆时针模式。当未受到扰动时, 两种模式是简并的, 但由于扰动的出现, 简并被打破, 导致谐振峰分裂成两个洛伦兹线形部分叠加的谐振峰, 如图2(b)所示。

模式展宽是由于微腔内部的散射效应引起的, 当光波与微腔内的散射体相互作用时, 部分光能会散射到自由空间, 导致谐振模式的能量分布在频率或波长上发生扩散, 形成谱线展宽^[16], 如图2(c)所示。

对于规则的球腔或柱形腔, 可以通过求解Maxwell方程组来获得回音壁模式的场分布, 通常由一组模式参数(p, q, l, m)来描述, 这些参数定义了模式的特性和频谱位置。其中, p代表的是模式的偏振(TE或TM偏振), q为径向模式数, 用于表明模式在环绕方向上的波数或环绕次数, 即模场沿径向分布的极大值的个数。l是角向模式数, 用于描述模式在垂直于环绕方向的平面上的波数, 可近似由公式l=2π n_effa/λ 获得, 在角向模式数增加时, 模式密度也随之增加, 可能会激发更多谐振模式, 从而提高传感器的灵敏度。m是方位角模式数, 表示模式在垂直平面上的位置, 一般取值范围为-l≤ m≤ l。对于微球腔的谐振波长更准确、 更可靠的近似可表示为:

λm=2πanr×(m0-αqm021/3-Lnratio2-1+3αq210×22/3m01/3+αqm0-2/321/3nratio2-13/2nratio2-23L2)-1(3)

式(3)中, m₀=m+ 12; n_m是谐振腔周围环境的折射率; n_r是微腔本身的折射率; n_ratio= nrnm是相对折射率; L是与偏振有关的系数, TE模式L=n_ratio, TM模式L= 1nratio; α _n是艾里函数的第q个零点, 当q=1时, α _q=2.338。谐振波长不仅与周围环境折射率和腔体折射率有关, 还与微腔尺寸和模式数有关。

为了深入理解WGM与模场分布的关系, 我们进行了折射率n_r=1.445 7, 半径R=20 μ m的液晶微球腔的仿真分析。图3展示了仿真后微球谐振腔的模式分布。其中, WGM的基模为q=1, l=m, 如图3(a)所示。通过对比图3中的(a)、 (b)和(c), 我们可以观察到m值越大, WGM的分布越集中于腔体赤道位置; 而m值越小, 模式越来越向两极发散分布。另外, 对比图3(a)和(d), 可以发现q值越大, WGM沿径向分布的极大值个数就越多。图3(e)为该微球腔的光强在454~472 nm波长范围内的谱线分布, 通过计算可以得到峰值对应的方位角模式数, 因此, 我们得到相应的FSR=1.65 nm。

图3

Fig.3

Figure Option ViewDownloadNew Window

图3 半径20 μ m液晶微球腔在不同模式数条件下的回音壁模式仿真分布图 (a): 模式数(q, l, m)=(1, 392, 392); (b): 模式数(q, l, m)=(1, 392, 391); (c): 模式数(q, l, m)=(1, 392, 390); (d): 模式数(q, l, m)=(2, 392, 392); (e): 该微球腔在454~472 nm范围内光谱Fig.3 Simulation of WGM spectrum of a 20 μ m liquid crystal microcavity with different modes number (a): (q, l, m)=(1, 392, 392); (b): (q, l, m)=(1, 392, 391); (c): (q, l, m)=(1, 392, 390); (d): (q, l, m)=(2, 392, 392); (e): The spectrum in the range of 454~472 nm

规则的WGM光谱谱线具有良好的洛伦兹线性和高斯分布, 结合1.1节中对FSR的讨论, 我们可以通过FSR确定WGM光谱峰值的个数或强度来定位中心目标谱线。一般地, 规则WGM光谱的中心谱线对应于微腔基本共振模式, 是具有最大光强度的共振模式, 即光波在这个模式下被最有效地捕获和储存, 谱线信噪比高。选择中心谱线可以获得良好的灵敏度, 用于监测微腔内介质的性质和对环境变化的响应。

实验中, 我们利用直径45 μ m的液晶微球进行胰蛋白酶传感, 实验结果如图4所示。在泵浦激光激励下, 液晶微球产生了规则的WGM光谱^[17]。呈现出对称性分布, 共振峰的数量为9个, 谱线展现出良好的洛伦兹特性和高斯分布, 且中心峰值与最高峰值重合。随着胰蛋白酶浓度的增加, 图4(a)显示光谱发生了相应的蓝移。由于WGM光谱中心谐振波长发生了移动, 则FSR也随之改变, 分布在1.67~1.85 nm之间, 但对于每一组WGM光谱而言, 其FSR保持不变。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 胰蛋白酶传感测量的液晶WGM光谱和灵敏度拟合曲线 (a): 不同浓度胰蛋白酶溶液下的WGM光谱; (b): WGM谐振波长与胰蛋白酶浓度变化关系曲线Fig.4 Liquid crystal WGM spectrum and sensitivity of trypsin sensing (a): WGM spectra under different trypsin concentrations; (b): Relationship between WGM resonance wavelength and trypsin concentration

因此, 我们选取中心谱线(也是最高峰)作为传感谐振峰, 拟合胰蛋白酶传感灵敏度曲线如图4(b)所示, 灵敏度为13.88 nm· (μ g· mL^-1)^-1, 线性度为0.991, 该结果具有较好的光谱对称性、 传感曲线高线性和实验测量合理性, 符合光谱标定三原则, 验证了该方法的可行性。

在基于液晶WGM传感测量的实际应用中, 理想完美的微球以及测量环境并不是总能满足, 因此外部和内部因素导致WGM光谱并非规则对称的。此时, WGM光谱出现谱线强度突变、 缺峰、 产生杂峰、 非正常劈裂等情况, 导致常规的选取中心峰值或者最强峰值的方法失效。因此, 一种合理的适用于非规则光谱的谱线标定方法是实现WGM传感测量的关键。

考虑到液晶WGM传感主要是基于谱线波长变化 (包括谱线移动、 谱线分裂、 展宽)来确定灵敏度, 所以准确标定谐振峰波长才是关键, 谱线强度并非首要因素。因此, 本文根据WGM光谱分布特性, 提出了基于SG滤波结合高斯平滑的非规则光谱标定方法, 并遵循光谱标定对称性、 高线性和合理性三原则实现谐振峰的标定。具体应用中, 根据非规则WGM光谱特性分为三类: (1)谱线缺峰和强度突变, 其原因主要是由于谐振条件的损耗变化所致; (2)谱线非规则劈裂, 液晶微腔中可能存在微小的缺陷或杂质, 导致光谱的非对称劈裂; (3)混合型变化光谱, 受到复杂测量环境的影响, 可能出现多种不规则变化。

2.2.1 WGM光谱缺峰和强度突变标定

WGM光谱的缺峰和强度突变主要表现为部分谱线缺失和光谱包络轮廓对称性破坏。如果整个WGM光谱的外包络完整, 且仅仅是相邻某些谱线缺失, 可以利用光谱FSR的均匀性分布特性实现对称性的缺失谱线补齐。但谱线缺峰往往会伴随谐振腔内能量的转移, 导致不同谐振峰的强度也发生变化, 则会扰乱包络分布的对称性, 无法进行谱线补齐。因此, 我们用SG滤波算法抽离光谱的伪连续谱, 然后再用高斯拟合的方法来获取光谱的中心, 以还原WGM光谱的对称性。SG滤波既可以实现平滑又可以去除噪声, 有效地过滤高频噪声、 保留信号特征并提高数据精度, 对于非线性信号也具有良好的适应性^[20]。其优点在于, 在平滑WGM光谱的同时, 能够更有效地保留伪连续谱的变化信息。再结合高斯拟合, 给出WGM光谱伪连续谱包络轮廓的对称性分布。最后, 选取离光谱中心点或者其他相对应的模式波长作为传感谐振峰, 实现WGM光谱的标定和传感测量。

为了验证可行性, 我们设计了pH传感实验。实验中引入海藻酸钠(sodium alginate, SA, 浓度为1.0 wt%)配置的水凝胶, 其目的是利用水凝胶对pH的敏感性引起液晶微腔的形变^[18]。这种形变并不是完美的球型变化, 因此液晶微腔的锚定作用并不是各向同性的, 从而导致WGM光谱中的谐振模式峰值缺失和强度突变, 实验结果如图5所示。在液晶微腔直径为70 μ m的情况下, 当环境溶液pH从6.86到4.55变化时, WGM光谱出现蓝移, 各个谐振模式的强度突变导致不再严格按照高斯分布, 中心波长和最大强度波长出现偏差, 谱线个数也不完全相同, 部分WGM光谱出现缺峰现象, 无法直接确定谐振峰的偏移。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 SA浓度1.0 wt%时pH传感测量的液晶WGM光谱和灵敏度拟合曲线 (a): 不同pH溶液下的WGM光谱; (b): WGM传感波长与pH变化关系曲线Fig.5 Liquid crystal WGM spectrum and sensitivity of pH sensing with SA concentration of 1.0 wt% (a): WGM spectra under different pH solutions; (b): WGM resonance wavelength shifts with pH variation

因此, 根据谱线标定三原则, 首先利用FSR谱线补齐对光谱进行对称性分析。在图5(a)中, 每一组WGM光谱中相邻的谱线FSR都是完整的, 因此不用再额外进行谱线补齐, 此时可以初步确定各个WGM光谱的波段范围。然后, 采用SG滤波抽离WGM光谱的伪连续谱, 如图5中绿色曲线所示, 伪连续谱的强度分布也全部覆盖了每一组的WGM光谱波段范围。之后利用高斯拟合标定伪连续谱中心位置, 此时光谱的对称性基本满足。高斯拟合的中心落在相邻两个峰的中间, 再分别选取左峰和右峰进行pH灵敏度拟合, 如图5(b)所示, 右峰的线性度低于左峰的拟合度, 灵敏度优于左峰, 但从实验的可靠性和稳定性角度考虑, 应选取高线性条件的左峰更为合理。

2.2.2 WGM光谱非规则劈裂标定

液晶微腔内可能存在的微小缺陷、 杂质等散射体, 或者能量耦合损耗变化, 造成WGM光谱的某些谱线出现非正常劈裂现象。当所有对应模式谱线都出现劈裂时, 可以基于相邻波数FSR近似相等的特性确定劈裂谱线的“ 左支” 或者“ 右支” 作为传感谐振峰。然而, 非正常劈裂往往不是所有谱线(或者对应模式)都分裂为“ 左支” 和“ 右支” , 同时还会造成WGM光谱的强度突变, 破坏光谱的对称性。因此, 仅采用FSR的分布特性无法实现光谱的准确标定。

我们设计了基于液晶WGM检测DNA的传感实验, 并采用十二烷基三甲基溴化铵(DTAB)作为中间敏感材料。在静电相互作用下, DTAB分子的极性基团探入液晶微腔表层的内侧, 引起液晶分子的锚定方向变化^[19], 导致激发的WGM光谱出现不同程度的非正常劈裂, 并伴随着峰值强度突变, 如图6所示。我们使用SG滤波和高斯拟合进行处理, 并选取高斯中心位置最近的谐振波长作为谐振峰。当DNA浓度为490 μ g· mL^-1时, 所要选取的谐振峰出现了非正常劈裂, 我们分别对“ 左支” 、 “ 右支” 以及中点值进行了波长拟合, 如图6(b)所示。对比结果显示, “ 左支” 具有最高的线性度。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 DNA传感测量的液晶WGM光谱和灵敏度拟合曲线 (a): 不同DNA浓度下的WGM光谱; (b): WGM谐振波长与DNA浓度变化关系曲线Fig.6 Liquid crystal WGM spectrum and sensitivity of DNA sensing (a): WGM spectra at different DNA concentrations; (b): Relationship between WGM resonance wavelength and DNA concentration

此外, 对于这种非正常的劈裂现象, 在劈裂程度不太大, 或者“ 左右支” 偏差较小时, 也可以通过相邻波数FSR近似相等的方法来辅助判断和选取“ 左右支” 或者中心值。在图6(a)中, DNA浓度为490 μ g· mL^-1时, 选取中心值和“ 左支” “ 右支” 得到的FSR是近似相等的, 都约为1.37 nm, 灵敏度和拟合度也只存在微小差距。

2.2.3 WGM混合型变化光谱标定

在液晶微腔WGM传感测量中, 复杂测量环境的影响也会造成光谱的混合型变化, 具有一定的随机性缺峰、 劈裂、 强度突变和杂峰等现象, 导致原始光谱几乎无法判断对称性, 难以进行谐振峰标定。我们仍然采用pH传感实验验证, 将SA的浓度减小至0.6 wt%, 降低形成的水凝胶机械强度, 增强随pH变化时液晶微腔的形变随机性, 实验结果如图7所示。每一组WGM光谱中随机出现了缺峰、 劈裂、 强度突变、 杂峰等现象, 其峰值个数、 FSR、 强度包络轮廓等都各不相同, 无法直接判断WGM谐振峰的漂移。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 SA浓度为0.6 wt%时pH传感测量的液晶WGM光谱和灵敏度拟合曲线 (a): 不同pH溶液下的WGM光谱; (b): WGM谐振波长与pH变化关系曲线Fig.7 Liquid crystal WGM spectrum and sensitivity of pH sensing with SA concentration of 0.6 wt% (a): WGM spectra under different pH solutions; (b): WGM resonance wavelength shifts with pH variation

根据光谱标定三原则, 首先根据FSR初步判断各个WGM光谱的波段范围, 再利用SG滤波和高斯拟合确定光谱中心位置, 还原光谱包络的对称性。再根据2.2.2节针对劈裂情况的讨论, 图7(a)中pH为6.86和4.55时的WGM谱线劈裂峰值非常接近, 可以选择中心波长作为谐振波长。此外, 当pH=5.43时, 高斯中心近似在两个峰的中心, 右峰拟合线性度高于左峰, 根据高线性原则选择右峰, 如图7(b)所示。同时, 根据实验条件变化, 选择右峰也更符合三原则的合理性。从实验测量过程可以看到, pH从6.00降到5.43再降到5.11的过程中, pH的变化量为2∶ 1, 因此在选择pH为5.43的谐振波长时, 确保所选取的谐振波长右峰更接近波长漂移量的2∶ 1位置处。

本实验和文献[18]采用了相同的实验设计, 对比后者的实验结果, 本文提出的谱线标定和三原则评判方法所获得的灵敏度和线性度与基本保持一致, 如图8所示。pH传感灵敏度分别为3.5和3.2 nm· pH^-1, 线性度分别为0.992和0.983, 验证了本方法的可靠性和可行性。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 SA浓度为0.6 wt%时pH传感测量的液晶WGM光谱和灵敏度拟合曲线[18] (a): 不同pH溶液下的WGM光谱; (b): WGM谐振波长与pH变化关系曲线Fig.8 Liquid crystal WGM spectrum and sensitivity of pH sensing with SA concentration of 0.6 wt% (a): WGM spectra under different pH solutions; (b): WGM resonance wavelength shifts with pH variation