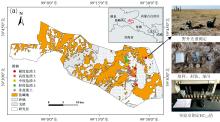
如图1(a)所示, 研究区域位于甘肃省张掖市肃南裕固族自治县明花乡(98° 47'—99° 33'E, 39° 20'—39° 46'N), 地处河西走廊中部, 巴丹吉林沙漠西缘, 地势平坦, 平均海拔1 381 m。研究区属于温带大陆性气候, 冬冷夏热, 降雨集中在夏季, 年平均降水量仅112.3 mm, 蒸发强烈^[14]。研究区地表覆被以盐碱地、 沙地和戈壁为主, 植被稀疏, 主要包括芨芨草、 红柳和榆树, 以及人工种植的梭梭育苗林场, 是西北典型土壤盐渍化区域。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区概况图Fig.1 Overview of the study area

土壤采样调查以现场测定取样与实验室测定相结合的方式, 如图1(b、 c、 d)所示。现场测定取样于2023年5月23日至5月27日进行, 根据区域可达性, 结合现有的数字土壤和土地利用/覆盖类型, 共选择了44个具有代表性的采样点。利用ASD FieldSpec^® 4 Standard-Res光谱辐射仪测定土样光谱反射率, 测定时间为10:00—15:00, 按照“ 五点取样法” 选取5个代表性位置, 每个位置连续测10次, 取平均值作为该采样点的光谱反射率值。测定完成即采集土样, 采样深度为10 cm, 将土样混合后装入密封防水袋中并记录采样点坐标, 以备下一步实验室测定与分析。现场取样完毕后, 将所有样品烘干、 研磨、 过0.15 mm筛, 取10 g土样配置土壤溶液(土样与蒸馏水的质量比为1∶ 5)^[15], 经搅拌、 静置、 沉淀后, 采用哈希HQ14d型电导率仪测定土壤溶液上清液电导率(EC_{1∶ 5}), 每个采样点测定3次, 取平均值作为该样点处的电导率。

根据整数阶微分理论, 函数f(x)的一阶微分定义为

f'(x)=limΔx→0f(x+Δx)-f(x)Δx(1)

式(1)中: Δ x为自变量x的增量。

与整数阶微分理论相比, 分数阶微分理论在发展过程中, 出现了多种定义形式, 以Grü nwald-Letnikov、 Riemann-Liouville、 Caputo三种形式应用最为广泛^[7]。

Grü nwald-Letnikov分数阶微分是由整数阶微分定义推广而来^[16], 对任意的α , 假设函数f(x)在区间[t₀, t]上有n+1阶连续导数, 则f(x)的(阶Grü nwald-Letnikov微分定义为

t0Dtαf(x)=limh→01hα∑j=0[(t-t0)/h](-1)jαjf(x-jh)(2)

(-1)jαj=α(α-1)…(α-j+1)j!(3)

式中: α 表示微分阶数, 符号D左右两侧的下标t₀和t分别表示积分的上限和下限, h为步长, [· ]为取整符号, (-1)^j αj表示二项式系数, j取1, 2, 3, …。

Riemann-Liouville分数阶是逐次不定积分的一种分数阶推广, 是通过将函数的积分表示为无穷级数来定义的, 设β > 0是任意正实数, n是大于β 的最小正整数, 即n-1≤ β ≤ n, 则f(x)的β 阶Riemann-Liouville微分定义为

t0Dtβf(x)=-1Γ(n-β)dndxn∫t0tf(τ)(x-τ)1+β-ndτ(4)

式(4)中: β 表示微分阶数, t₀和t分别表示积分的上下限, Γ (· )为Gamma函数, τ 为中间变量, 即先做n-β 次积分, 再求n次导数^[17]。

Caputo分数阶微分定义与Riemann-Liouville类似, 用几乎相同的方法推广经典的整数阶微分, 区别在于它们的微积分顺序不同, 设ν > 0且n-1< ν ≤ n, n是大于ν 的最小正整数, 则f(x)的ν 阶Caputo微分定义为

t0Dtνf(x)=1Γ(n-ν)∫t0t(x-τ)n-ν-1f(n)(τ)dτ(5)

式(5)中: ν 表示微分阶数, t₀和t分别表示积分的上下限, Γ (· )为Gamma函数, τ 为中间变量^[18]。

由于ASD FieldSpec^® 4 Standard-Res光谱辐射仪的重采样间隔为1 nm, 因此在以上公式中, h取为1。

变异系数(coefficient of variation, C.V)是反映数据离散程度的度量指标^[19]。参考前人的研究成果并结合实际情况, 本研究通过实际测试与验证, 选取0~16%为小变异, 16%~36%为中等变异, 大于36%为高度变异的波段变异系数分级标准^[20]。其表达式如式(6)—式(8)

C.V=SDMean×100%(6)

SD=n-1∑i=1n(xi-Mean)2(7)

Mean=n-1∑i=1nxi(8)

式中: SD为样本标准差, Mean为样本均值, n为样本数量。

皮尔逊相关系数(Pearson correlation coefficien, PCC)是反映变量之间相关关系密切程度的统计指标^[19]。在光谱定量分析过程中, 某波段的光谱反射率与地表参数的相关性越高, 说明该波段光谱响应越敏感, 在光谱建模中该波段也就越有可能作为特征波段进入后续定量模型的建立^[7]。给定两个变量X、 Y, 那么两个变量间的相关系数可通过式(9)计算

PCCX, Y=cov(XY)σXσY=E(XY)-E(X)E(Y)E(X2)-E2(X)E(Y2)-E2(Y)(9)

式(9)中: cov(· )表示求协方差, E(· )表示求数学期望, σ _X和σ _Y分别为变量X和Y的标准差。

由研究区土壤样本电导率EC_{1∶ 5}(dS· m^-1)值统计特征(表1)可知, 土壤电导率最大值为19.18 dS· m^-1, 最小值为0.226 dS· m^-1, 平均值为7.095 dS· m^-1, 变异系数为85%, 属于中等变异程度, 土壤样本具有较高的离散性。依据土壤盐渍化程度分级标准和已有研究成果^[21], 土壤样本中非盐渍土(0~2 dS· m^-1)、 轻度盐渍土(2~4 dS· m^-1)、 中度盐渍土(4~8 dS· m^-1)、 高度盐渍土(8~16 dS· m^-1)和极高盐渍土(> 16 dS· m^-1)均有采集, 土壤样本类型全面。

表1

Table 1

表1(Table 1)

表1 土壤样本EC1∶ 5(dS· m-1)值统计特征 Table 1 Statistical characteristics of EC1∶ 5(dS· m-1) values of soil samples 样本类型 样本 数量 最大值 最小值 平均值 标准差 变异 系数/% 极高盐渍土 5 19.18 16.14 17.925 1.297 7.2 高度盐渍土 14 15.72 8.46 12.049 2.088 17 中度盐渍土 4 7.18 4.64 6.045 1.036 17 轻度盐渍土 6 3.67 2.097 2.865 0.589 21 非盐渍土 15 1.908 0.226 1.081 1.089 101 总体样本 44 19.18 0.226 7.095 6.027 85

表1 土壤样本EC1∶ 5(dS· m-1)值统计特征 Table 1 Statistical characteristics of EC1∶ 5(dS· m-1) values of soil samples

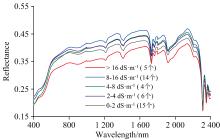
考虑到ASD FieldSpec^® 4 Standard-Res 光谱辐射仪系统误差和测量环境噪声的影响, 需对实验测定光谱进行预处理去噪。首先, 利用Savitzky-Golay平滑滤波方法对测定的光谱进行平滑处理。其次, 删除了位于低信噪比的波段, 即350~399和2 401~2 500 nm^[21]。土样光谱反射率测定结果如图2所示。由于研究区选取在典型的土壤盐渍化区域, 高度盐渍土和极高盐渍土采集的样本占比较高(43%, 19个), 轻度盐渍土和中度盐渍土采集的样本占比较低(23%, 10个), 非盐渍土土样15个, 占比为34%。各等级间土样光谱曲线差异明显, 易于区分, 也验证了高光谱反演盐渍土的可行性。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 土样光谱反射率测定结果Fig.2 Results of spectral reflectance measurement of soil samples

通过编程实现Grü nwald-Letnikov、 Riemann-Liouville、 Caputo分数阶微分处理函数, 且分数阶微分阶数间隔取为0.1, 起始阶数为0.1阶, 终止阶数为1阶, 不同分数阶微分定义形式下各有10种微分处理方式, 共30种。

图3分别绘出了从0.1阶到1阶不同分数阶微分定义形式下微分处理结果。从图3可以看出, 土样光谱反射率曲线在不同分数阶微分定义形式下同阶微分处理后表现出较大差异, Riemann-Liouville分数阶微分处理后表现尤为明显。然而, Grü nwald-Letnikov分数阶微分与Caputo分数阶微分处理后土样光谱反射率曲线结果类似, 在0.1到0.4阶范围内, 土样光谱反射率曲线变化趋势一致, 从0.4到1阶范围内, 土样光谱反射率值仅在某些波段区间表现出差异。如图3(j)所示, 随着分数阶阶数的增加, 光谱反射率微分值逐渐降低且向0值逼近。当微分阶数为1时, 经Grü nwald-Letnikov、 Riemann-Liouville、 Caputo分数阶微分处理后, 三条土样光谱反射率曲线重合, 也从侧面验证了当阶数为1时, Grü nwald-Letnikov、 Riemann-Liouville、 Caputo分数阶微分理论与整数阶微分理论相一致。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 土样光谱反射率曲线微分处理结果 (a)—(j)分别为0.1阶至1阶Fig.3 Differential processing results of reflectance spectra of soil samples (a)—(j): Responding to the order from 0.1 to 1, respectively

分数阶微分的意义在于它描述了函数曲线的“ 一般斜率” , 在光谱分析中可以被视为光谱曲线的细微变化率。对于0.1阶微分而言, 它反映了函数变化率的一个较为平滑的、 分布更广的变化趋势, 由于0.1接近于0, 它倾向于强调函数值在较长区间上的缓慢变化, 而不是局部的快速变化。然而, 0.9阶微分则更倾向于强调函数在较短区间内的快速变化, 由于0.9接近于1, 它突出了函数值的局部变化特征, 尤其是那些快速波动或边缘效应, 可以捕捉到函数行为中的细微波动和突变。已有研究表明分数阶微分具有对光谱反射率曲线斜率的“ 敏感性” , 即随着分数阶阶数的增加, 各阶微分曲线缓慢逼近1阶微分曲线^[7], 这与本工作的处理结果一致。分数阶微分处理的优势在于能够提供函数在这一点附近的整体变化趋势的信息, 这种描述更具有全局性, 有助于捕捉到传统整数阶微分可能忽略的光谱特征, 从而提供更全面的光谱信息。

在不同分数阶微分定义形式下, 对原始光谱反射率数据进行微分处理后, 得到每个波段的变异系数, 并统计微分处理后各变异波段数量。图4绘制了小变异(0< C.V< 16%)、 中等变异(16%≤ C.V≤ 6%)以及高度变异(C.V> 36%)的波段数量随微分阶数增加的变化趋势, 图4(a)—(c)分别为Grü nwald-Letnikov、 Riemann-Liouville和Caputo分数阶微分处理后不同变异强度波段数量随微分阶数增加的变化趋势图。由图4可见, 随着微分阶数的增加, Grü nwald-Letnikov、 Riemann-Liouville、 Caputo分数阶微分处理后高度变异的波段数量均呈现出增加的趋势。Grü nwald-Letnikov、 Riemann-Liouville分数阶微分处理后小变异的波段数量呈现减少的趋势, 中等变异的波段数量呈现出先增加、 后减少的趋势, 且在0.8、 0.9阶处达到极值点。Caputo分数阶微分处理后, 小变异的波段数量先增加后减少, 在0.5阶处达到最大值, 中等变异波段数量先减少、 后增加、 再减少的趋势, 且在0.5阶处为极小值点, 在0.7阶处达到极大值点, 总体为减少趋势。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 土样光谱数据微分处理后小变异、 中等变异及高度变异的波段数量 (a): Grü nwald-Letnikov分数阶; (b): Riemann-Liouville分数阶; (c): Caputo分数阶Fig.4 Number of bands with small, medium, and high variability after differential processing of soil sample spectral data (a): Grü nwald-Letnikov; (b): Riemann-Liouville; (c): Caputo

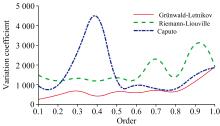
对原始光谱反射率各分数阶微分后全波段变异系数进行统计, 如图5所示。经Grü nwald-Letnikov、 Riemann-Liouville分数阶微分处理后土样光谱数据, 随着阶数的增加, 全波段变异系数呈现出增加趋势, 经Riemann-Liouville分数阶微分处理后土样光谱数据在0.7阶、 0.9阶时的全波段变异系数超过了1阶。经Caputo分数阶微分处理后土样光谱数据, 随着阶数的增加, 全波段变异系数表现出先增加、 后减少、 再增加的变化趋势, 且全波段变异系数在0.3、 0.4阶超过了1阶。Riemann-Liouville、 Caputo分数阶微分处理后土样光谱数据全波段变异系数极值点对应的阶数, 均为分数阶, 只有经Grü nwald-Letnikov分数阶微分处理后土样光谱数据全波段变异系数最大值在整数阶1处。结合上节结论得出, 随着微分阶数的增加, 光谱反射率微分值趋于0, 波动范围逐渐减小, 而光谱数据的变异性随着分布范围的减小而增强。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 土样光谱数据微分处理后全波段变异系数变化趋势Fig.5 Trend of variation coefficient in full band after differential processing of soil sample spectral data

绘制了土样光谱反射率数据与电导率数据在不同分数阶微分定义形式下的相关系数图, 并在0.01水平下检验相关系数的显著性, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 微分处理后光谱数据与EC1∶ 5的相关系数图 (a)—(j)分别为0.1阶至1阶Fig.6 Correlation coefficient between differential processed spectral data and EC1∶ 5 (a)—(j): Responding to the order from 0.1 to 1, respectively

图6分别给出了不同分数阶微分定义形式下, 0.1~1阶微分处理后光谱数据与EC_{1∶ 5}的相关系数图(图中p^{* *} 表示通过0.01水平下显著性检验)。由图6可以看出, 未经分数阶微分处理的土样光谱曲线在0.1~1阶之间没有任何波长通过0.01水平下显著性检验。不同分数阶微分处理后的土样光谱曲线在0.1~1阶范围内与电导率相关性响应各不相同。当阶数为1时, 不同分数阶微分处理后相关性响应趋于一致, 符合Grü nwald-Letnikov、 Riemann-Liouville、 Caputo分数阶微分定义在整数阶为1时等价的前提条件。

为更加直观的分析不同分数阶微分处理后土样光谱曲线与电导率的相关性, 统计并绘制了通过0.01水平下显著性检验的波段数量随阶数增加的变化趋势如图7所示。可以发现, 经Riemann-Liouville分数阶微分定义处理后, 通过显著性检验的波段数量变化较小, 与整数阶(1阶)微分处理结果基本一致。经Grü nwald-Letnikov、 Caputo分数阶微分处理后, 在0.1~0.3阶范围内, 通过0.01水平下显著性检验的波段数量为零。在0.3~1阶范围内, 通过显著性检验的波段数量总体表现出先增加后减少的趋势。Grü nwald-Letnikov分数阶微分处理在0.9阶时通过显著性检验的波段数量达到最大值, Caputo分数阶微分处理在0.8阶时通过显著性检验的波段数量达到最大值, 且通过显著性检验的波段数量大于1阶导数处理后的波段数量, 由此可以得出: Grü nwald-Letnikov和Caputo分数阶微分处理能够增加通过0.01水平下显著性检验的波段数量, 扩大模型输入变量的选择范围。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 通过0.01水平下显著性检验的波段数量Fig.7 Number of wavebands passed significance test at 0.01 level

参考前人的研究成果, Dehaan等^[22]在野外测量了不同类型盐渍化土壤光谱, 应用连续统去除法分析了光谱数据, 结果表明土壤在1 915和2 205 nm附近有吸收特征峰。田安红等^[10]通过统计分数阶微分值与含盐量的相关系数最大绝对值及其对应波段, 发现0.6~0.9阶最大相关系数对应的波段出现在1 802和1 803 nm。Weng等^[23]研究发现, 土壤盐分在1 911、 2 203和2 345 nm波段附近存在吸收峰, 吸收峰强度与土壤盐分含量存在显著的正、 负相关关系, 这些吸收峰构成了高光谱遥感土壤盐分的敏感波段。

统计了不同分数阶微分变换形式下, 土壤光谱曲线微分值与电导率值相关系数最大绝对值所对应的波段, 如表2所示。结果发现: 不同分数阶微分变换形式得到的敏感波段与前人研究结果基本保持一致, 属于近红外长波(1 100~2 526 nm); 敏感波段在一定范围内随阶数的变化而变化。

表2

Table 2

表2(Table 2)

表2 不同分数阶相关系数最大绝对值及其对应波段 Table 2 Absolute values of maximum correlation coefficients of different fractional orders and their corresponding bands 阶数 Grü nwald-Letnikov分数阶 Riemann-Liouville分数阶 Caputo分数阶 最大绝对值 波段/nm 最大绝对值 波段/nm 最大绝对值 波段/nm 0.1 0.358 2 307 0.619 2 386 0.368 530 0.2 0.368 2 296 0.611 2 386 0.355 530 0.3 0.376 2 278 0.616 1 916 0.404 1 001 0.4 0.463 2 205 0.622 1 916 0.488 2 205 0.5 0.594 2 212 0.627 1 916 0.598 2 205 0.6 0.703 2 216 0.631 2 002 0.622 2 182 0.7 0.685 2 212 0.639 2 002 0.664 2 175 0.8 0.640 2 142 0.645 2 002 0.647 2 142 0.9 0.642 2 143 0.649 2 002 0.645 2 143 1 0.642 1 916 0.642 1 916 0.642 1 916

表2 不同分数阶相关系数最大绝对值及其对应波段 Table 2 Absolute values of maximum correlation coefficients of different fractional orders and their corresponding bands

在盐渍土电导率高光谱反演中, 通常选择波段与土壤电导率相关系数绝对值较高的进行建模。已有研究表明: 只要分数阶微分值与土壤电导率的相关系数大于整数阶与土壤电导率的相关系数且相关系数提升的百分比足够大, 则可证明分数阶可以提高光谱预处理的精度及建模精度^[10]。

为探讨不同分数阶微分定义形式下, 微分处理后光谱反射率值与土壤电导率的相关系数及相关系数提升百分比, 表3统计计算了不同分数阶相关系数绝对值及相关系数提升百分比。结果表明: 分数阶和整数阶(1阶)微分处理后的光谱反射率值与土壤电导率的相关系数均大于未处理时(0阶)的相关系数。对比分析不同分数阶处理结果, Grü nwald-Letnikov分数阶微分在0.6阶、 0.7阶和0.8阶处理效果优于整数阶(1阶), 相关系数提升百分比为9.5%、 6.7%、 0.3%。Riemann-Liouville和Caputo分数阶微分处理效果分别在0.8~0.9阶、 0.7~0.9阶有所提升, 但是效果提升不是很明显, 相关系数提升百分比几乎都在1%左右。

表3

Table 3

表3(Table 3)

表3 不同分数阶相关系数绝对值及相关系数提升百分比 Table 3 Absolute values of correlation coefficients of different fractional order and percentage increase of correlation coefficients 阶数 Grü nwald-Letnikov分数阶 Riemann-Liouville分数阶 Caputo分数阶 0.1 0.358/-44.2% 0.619/-3.6% 0.368/-42.7% 0.2 0.368/-42.7% 0.611/-4.8% 0.355/-44.7% 0.3 0.376/-41.4% 0.616/-4.0% 0.404/-37.1% 0.4 0.463/-27.9% 0.622/-3.1% 0.488/-24.0% 0.5 0.594/-4.8% 0.627/-2.3% 0.598/-6.9% 0.6 0.703/+9.5% 0.631/-1.7% 0.622/-3.1% 0.7 0.685/+6.7% 0.639/-0.5% 0.664/+3.4% 0.8 0.640/+0.3% 0.645/+0.5% 0.647/+0.8% 0.9 0.642/0.0% 0.649/+1.1% 0.645/+0.5% 1 0.642/- 0.642/- 0.642/- 注: 相关系数提升%=(AA-BB)/BB, AA表示分数阶相关系数绝对值, BB表示整数阶相关系数最大绝对值 Note: Pearson correlation coefficien (PCC) increase percentage %=(AA-BB)/BB, AA represents the absolute value of fractional PCC, BB represents the maximum absolute value of PCC of integer order

表3 不同分数阶相关系数绝对值及相关系数提升百分比 Table 3 Absolute values of correlation coefficients of different fractional order and percentage increase of correlation coefficients