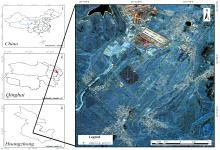
研究区位于中国青海省西宁市湟中区, 地处湟水流域中游地带, 地理经纬度范围介于东经101° 09'32″—101° 54'50″, 北纬36° 13'32″—37° 03'19″(图1)。研究区属于高原干旱-半干旱大陆性气候, 常年高寒、 干旱, 地理环境上属于典型农牧交错带, 生态环境脆弱, 植被类型以温性草原为主, 主要土壤类型为栗钙土和灰钙土。受限于地理环境因素, 农业是区域经济发展的重要支柱产业。因此, 快速掌握耕地土壤养分空间分布情况对合理规划和管理耕地、 提高作物品质和产量具有指导作用, 对该地区的社会经济发展具有一定的现实意义。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区采样点分布图Fig.1 The spatial distribution of soil samples

1.2.1 土壤样品采集和处理

2021年5月在试验区内挑选典型耕地地块区域, 利用五点混合法进行土壤采样, 以采样点位置为中心, 在其周围5 m× 5 m范围内, 采集5份0~15 cm深度内表层土壤样本并充分混合放入密封袋, 共采集了67个耕地土壤样本, 采样过程中利用手持GPS记录了样品地理坐标信息。样本由密封袋装入带回实验室, 剔除杂物、 风干研磨过筛保存。参照《土壤农业化学分析方法》, 利用重铬酸钾容量法测定SOM含量。统计结果发现SOM含量值域在10.6 ~39.6 g· kg^-1, 均值为24.16 g· kg^-1, 总体数值偏低, 变异含量系数为22.94%, 属于中等变异。按照含量值将样品由高到低分为17组, 从每组中随机选择1个样品作为验证样本, 则验证集和训练集样本数量分别是17和50。

1.2.2 影像数据获取和处理

ZY1-02D卫星是中国自然资源部于2019年9月发射的首颗民用高光谱业务卫星。光谱覆盖范围为400~2 500 nm, 高光谱相机幅宽60 km, 空间分辨率30 m, 其中可见光-近红外76个波段, 光谱分辨率10 nm; 短波红外90个波段, 光谱分辨率20 nm。本次使用ZY1-02D高光谱影像过境时间为2021年5月8日, 临近样品采样时间, 并对影像进行了预处理。由于高光谱短波红外波段数据中条纹明显, 选择“ 全局去条纹” 方法进行了条纹修复。剔除掉重叠波段后, 可见光-近红外和短波红外波段合并共153个光谱波段数据, 最后利用GIS软件平台对影像进行了大气校正、 辐射校正和几何校正, 以获得地物真实反射率。

微分是对函数局部变化率的一种表示, 在对影像像元进行微分计算时, 影像灰度值恒定的区域微分值为0, 灰度台阶或者斜坡低点处微分值不为0。FOD是对整数阶微分的扩展, 具体计算公式如式(1)^[15]

daf(λ)=limh→01ha∑m=0t-s/h(-1)mΓ(α+1)m!Γ(α-m+1)f(λ-mh)(1)

式(1)中, λ 为高光谱波长; f(λ )为λ 的函数; α 是分数阶次, 当α 是整数的时候, 该公式可以计算整数阶, 是分数便可计算分数阶, h为步长, t与s分别表示微分的上限和下限, Γ 是Gamma函数, 在本文研究中, h设置为1, s、 t分别为起止波长(350 nm, 2 500 nm)。从公式中可以看出, λ 波长的导数值受到相邻波长反射率影响, 越近影响越大, 故选择影像高光谱反射率数据以0.2阶为间隔进行0~2阶的分数阶微分处理, 以期可以保留和放大更多的光谱特征。

竞争性自适应重加权采样法(competitive adapative reweighted sampling, CARS)是一种变量优化选择算法, 可进一步去除光谱信息噪声与冗余的特征变量, 使得建模效果更优。该算法具有竞争性, 可以解决变量之间多重相关性的问题, 将蒙特卡洛采样和最小二乘模型回归系数结合用于特征波段选择^[23]。算法过程是借助自适应重加权采样技术和指数衰减函数找出最小二乘模型中对应系数绝对值大的波长变量, 以回归系数和交互验证均方根误差(RMSECV)为指标, 将小回归系数值的波段删除, 通过十折交互检验获取到的RMSECV最小的变量子集即是对应的特征波段。

CARS算法在特征选择过程中存在采样的随机性导致算法的不稳定。变量的稳定性不能只考虑模型回归系数, 还要考虑回归系数的稳定性, 这个稳定性定义为回归系数的绝对值除以标准差。2012年提出的sCARS算法正是基于这个理论^[24], 通过计算得到稳定性高的变量被认为是重要变量, 所以与CARS不同的是选择将变量的稳定替代回归系数的绝对值作为衡量变量选择的指标, 以此增加特征选择结果的稳定性。因此为了结果的稳定性选择采用sCARS算法进行特征波段提取。

选择4种机器学习框架构建有机质反演估测模型, 分别是随机森林(random forest, RF)、 极端提升树(gradient boosting decision tree, GBDT)、 极限学习机(extreme learning machine, ELM)和岭回归(ridge regression, RR)算法。GBDT属于一种决策树与Boosting串行式集成学习思想相结合的算法, 是一种将多个弱学习器加权组合为强学习器的集成学习模型。RF是基于Bagging并行式集成学习思想开发算法, 全部决策树组合成随机森林, 预测结果取平均值作为回归值。决策树的生成过程体现两次随机选择, 一是分类树的特征点随机分裂生成决策树, 二是所有分类树随机有随机森林生成。ELM属于单隐层前馈神经网络学习训练模型, 算法结构由输入层、 隐含层和输出层组成, 通过神经元进行连接。RR属于多重共线性数据分析有偏估计线性回归算法, 以损失部分信息或降低拟合精度为代价, 舍弃了最小二乘法的无偏性, 使得到的估计结果更加稳定, 均方误差更小。

利用随机搜索和网格搜索两种方法进行机器学习模型超参数优化, 网格搜索方法属于枚举遍历性质的搜索算法, 模型各个超参数进行组合配置后, 采用遍历的算法对每一个配置进行计算评估, 选择出最优的超参数组合方法; 随机搜索算法是对模型的超参数进行随机组合, 然后对组合的配置进行计算, 选出最优配置。

均方根误差(RMSE)、 决定系数(R²)和相对分析误差(RPD)作为评价预测模型优劣的指标。RMSE代表模型预测精度, 其值越小说明模型估测效果越好。R²代表预测模型的拟合能力, 取值范围0~1, 越接近于1代表模型拟合效果越高, 性能越稳定。RPD数值大表示模型预测能力优秀, 如果RPD≤ 1.4, 表示模型不具备预测能力, RPD> 2.0, 表明预测效果极好^[25]。

样本高光谱影像原始光谱曲线如图2所示, 图中可知所有样品光谱反射率最高不超过0.4, 所有光谱曲线走向趋势相似, 可见-近红外范围内反射率值一直增大; 受空气中水蒸气的影响, 短波红外处有两处明显的波谷, 分布在1 500和2 000 nm处, 光谱整体趋势呈现出先增长后下降的趋势。

图2

Fig.2

	Figure Option ViewDownloadNew Window
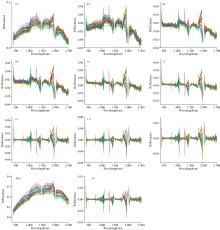	图2 原始与微分处理后光谱反射曲线图Fig.2 The original and fractional-order differential transform reflectance spectra

以0.2为一个步长从0~2进行光谱微分变换, 以期达到放大光谱曲线波峰波谷和去噪的目的, 充分挖掘与有机质含量相关的潜在波段信息, 为后续反演模型的建立提供基础数据支持。原始光谱数据经过预处理后, 光谱变化特征均发生了明显变化, 结果如图2所示, 0.2阶微分处理后光谱曲线波峰波谷和反射率值变化较小, 其余微分处理后均发生了较明显的变化, 波峰波谷数量较多且反射率值有较大起伏, 较为明显的波峰波谷分布在1 000、 1 250、 1 500和2 000 nm, 经过一阶微分和二阶微分处理后, 在1 750~2 000 nm波段范围内, 光谱反射率值波动较大。

利用SPSS软件计算SOM含量与土壤光谱反射率的皮尔森相关系数, 利用Origin软件绘制系列图件。如图3所示, 随着波长的增加, 原始光谱反射率与有机质含量相关性大致呈现正相关, 曲线有轻微的波动, 但是相关性总体较低, 数值处于-0.3~0.3之间。经过不同阶次微分变换后的光谱与SOM含量进行相关性分析, 结果如图3所示, 除了0.2分数阶变换, 其余变换形式后光谱与SOM含量相关性较原始光谱数据比较均有了不同程度的提高(表1), 且部分分数阶变换后效果优于整数阶(一阶, 二阶)变换, 说明分数阶比整数阶展示出了更优越的数据挖掘能力。0.4阶和0.6阶微分变换相关性特征趋势大致相同, 数值上0.6阶微分变换稍高, 0.8阶微分变换相关性系数变化趋势和数值出现变化, 数值波动较大, 较高值位于500、 1 200、 1 600和2 400 nm处, 最高值达到了-0.783, 对于波段2 434 nm, 1.2阶、 1.4阶、 1.6阶和1.8阶微分变换可明显看出相关性系数趋势相近且数值波动更为频繁, 充分说明了微分变换可以发掘出更多与SOM产生响应关系的光谱信息, 相关性系数值较高出现在500、 700、 1 200和2 400 nm处, 且最高值均处于2 400 nm附近。不同变换形式下通过皮尔森相关系数阈值的敏感波段数目不一, 1.8阶微分处理后最高, 达到36个, 虽然0.8阶微分通过波段数小于其他变换形式(25个), 但是从相关性数值上看, 0.8阶变换后相关性系数普遍较高且具有最高值, 说明其可以有效增强SOM光谱特征。有文献指出可能受高光谱影像、 样本数量和有机质含量影响, 不同来源的影像高光谱反演有机质最优阶数小于1阶, 而地面高光谱反演最优阶数大于1阶。本研究反演最优阶数为0.8, 与已有研究成果一致^[26]。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同阶次微分处理后相关性计算结果图(剔除水蒸气影响波段)Fig.3 Soil spectral correlation coefficient curves of different fractional-order transformations(Removing bands affected by water vapor)

表1

Table 1

表1(Table 1)

表1 不同阶次微分处理后相关性计算计算结果 Table 1 Maximum correlation coefficients and sensitive bands for different order fractional derivative processings 阶次 敏感波段 数量 相关性绝对 值最大 最大值对应 波段/nm 皮尔森 相关系数 计算结果 0 0 -0.237 396 0.2 0 0.186 765 0.4 21 0.462 2 250 0.6 19 0.496 1 712 0.8 25 -0.783 2 434 1 16 -0.659 1 947 1.2 27 -0.649 2 434 1.4 28 -0.600 2 434 1.6 28 0.609 2 451 1.8 29 0.649 2 451 2 10 0.662 1 964

表1 不同阶次微分处理后相关性计算计算结果 Table 1 Maximum correlation coefficients and sensitive bands for different order fractional derivative processings

高光谱数据波段存在冗余现象, 为了提升建模精度本研究选择使用sCARS算法进行波段筛选实验, 结果如图4所示。图4(a)从上往下依次是变量变化趋势、 十折交叉均方根误差和变量回归系数图。可以看到随着算法迭代次数的增加, 指数衰减函数使得算法保留的波段越来越少, 并且减少速度越来越慢。这也说明了sCARS算法在特征波长挑选变量过程中存在粗选和精选两个选择阶段。图中均方根误差随着迭代次数的变化有一定的波动, 当运行到24次的时候误差最小, 说明此时建模效果最优, 0~24次代表了模型在不断剔除较不敏感的波段, 以此来达到不断优化模型的目的。运行24次之后, 不断剔除波段后的结果却影响模型的精度, 表示此后删除的波段与有机质含量相关性较大。最小变量子集所对应回归系数如图4(a)所示, 子集包括波段15个, 图4(b)是sCARS算法筛选出的15个特征波段的分布情况。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 特征波段提取结果Fig.4 Result of feature band extraction

综合考虑准确性和差异性, 选择GBDT、 RF、 ELM和RR分别构建SOM估测模型。其中, GBDT和RF分别采用Boosting和Bagging的集成学习方式, 拥有出众的学习能力。ELM是单隐层前馈神经网络学习训练的新模型, 运行速度快, RR通过在损失函数中加入L2正则项来缓冲和防止样本个数少引起的过拟合现象, 参数简单, 训练速度快, 而且可以防止模型的过拟合现象。

2.4.1 机器学习模型参数优化

在利用机器学习模型进行回归预测时, 有效地确定机器学习的超参数意义重大。结合随机搜索和网格搜索进行超参数设置, 第一步是在较大范围内随机搜索最优点, 属于粗选, 第二步是在最优点附近运用网格搜索法细选出最优结果。通过计算各模型在测试集上的均方根误差来确定各模型的最优超参数组合, 计算结果如表2所示。

表2

Table 2

表2(Table 2)

表2 不同机器学习模型超参数优化计算 Table 2 Predictive index results for different machine learning models 模型 超参数 RMSE /(g· kg-1) RF n _estimators=80, max_depth=5 1.84 GBDT learning_rate=0.01, subsample=0.9, n_estimators=150, max_depth=3 2.41 ELM Number of neuron nodes=10 2.48 RR alpha=1 2.92

表2 不同机器学习模型超参数优化计算 Table 2 Predictive index results for different machine learning models

2.4.2 模型构建与分析

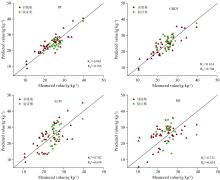
将经过FOD-sCARS方法提取特征波段的像元光谱和全波段光谱作分别作为模型输入变量, 样品SOM含量作为输出端, 选择随机搜索和网格搜索优化计算得到的超参数值作为各学习器超参数设定值, 为了对比分析不同模型输入因子和不同机器学习估测模型的预测性能, 对各模型在训练集和验证集的各项评价指标进行了计算(表3)。

表3

Table 3

表3(Table 3)

表3 不同机器学习估测指标结果 Table 3 Estimation index results for different machine learning models 模型 RC2 RMSEC RP2 RMSEP RPD SOM FOD-sCARS 特征波段 RF 0.843 1.431 0.766 2.995 1.86 GBDT 0.814 1.893 0.704 3.396 1.64 ELM 0.742 2.001 0.638 3.689 1.51 RR 0.725 2.168 0.624 3.641 1.53 全波段 RF 0.766 1.845 0.712 3.459 1.61 GBDT 0.712 2.013 0.608 3.922 1.42 ELM 0.634 2.538 0.549 4.312 1.29 RR 0.648 2.417 0.557 4.22 1.32

表3 不同机器学习估测指标结果 Table 3 Estimation index results for different machine learning models

各项评价指标计算结果表明, 将全波段光谱作为模型输入变量所构建的模型估测结果普遍低于特征波段光谱变量估测模型, 说明FOD-sCARS方法所提取的特征波段可以大大提高模型估测效果。4种机器学习模型均能达到预测SOM含量的目的, ELM和RR预测精度相对较低, RF和GBDT两种集成学习模型预测精度较高, 其中RF预测效果最优, Rp2为0.766, PRD为1.86。RR可以解决多重共线问题, 但由于本研究中样本数量较少, 可能使得预测效果低于其他模型, ELM在运行过程中由于权重初始值是随机的, 使得模型运算速度快, 但同时也令模型性能不稳定, 在预测效果上低于其他模型。拟合效果图可以验证不同模型拟合结果(图5), 从拟合图上可以看出RF预测模型样点预测值与真实值分布更接近于1∶ 1拟合线, 且分布较为均匀。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同模型预测结果拟合图 (a): RF; (b): GBDT; (c): ELM; (d): RRFig.5 Scatter plots of the predicted values against measured values of different inversion models (a): RF; (b): GBDT; (c): ELM; (d): RR

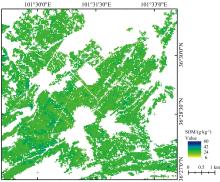
结合特征光谱波段选择, 以ZY1-02D高光谱影像数据为输入数据, 采用RF机器学习模型对研究区裸土区域SOM含量进行估测, 并基于GIS软件平台, 绘制研究区SOM含量空间分布图(图6)。为了提高研究区SOM含量估测及制图的精度, 采用裸土指数方法提取影像裸土像元。从反演结果图可以看出, 研究区耕地部分有机质含量呈现中等水平, 从空间分布来看, 研究区东北部有机质含量较西南部略低, 有机质含量值最高的地方处于研究区西南部。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 基于RF模型土壤有机质含量空间分布图Fig.6 Spatial distribution of SOM based on RF model