引用本文
陈旭, 曹思珩, 杨仁敏, 陈秋宇, 李建国, 徐璐. 基于光谱技术的典型互花米草入侵湿地土壤属性预测研究[J]. 光谱学与光谱分析, 2025,45(1): 197-203.
CHEN Xu, CAO Si-heng, YANG Ren-min, CHEN Qiu-yu, LI Jian-guo, XU Lu. Using Spectroscopy to Predict Soil Properties on Coastal Wetlands Invaded by Spartina Alterniflora [J]. Spectroscopy and Spectral Analysis, 2025,45(1): 197-203.
Doi:10.3964/j.issn.1000-0593(2025)01-0197-07  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于光谱技术的典型互花米草入侵湿地土壤属性预测研究
陈旭, 曹思珩, 杨仁敏, 陈秋宇, 李建国, 徐璐*
江苏师范大学地理测绘与城乡规划学院地理信息科学系, 江苏 徐州 221116
*通讯作者 e-mail: luxa1023@jsnu.edu.cn

作者简介: 陈 旭, 女, 1997年生, 江苏师范大学地理测绘与城乡规划学院硕士研究生 e-mail: 1621324885@qq.com

收稿日期: 2023-02-21 修订日期: 2024-03-26
基金: 国家自然科学基金项目(42371053, 42271287, 42171054), 江苏省海洋科技创新项目(JSZRHYKJ202212), 江苏师范大学科研与实践创新计划校级项目(2021XKT0089)资助
摘要

为了高效监测互花米草入侵海岸带湿地生态系统的土壤属性变化, 选取江苏省盐城湿地珍禽国家级自然保护区的一处典型互花米草入侵湿地作为研究区, 利用随机分层采样方法选取15个样点, 在3个深度(0~30、 30~60、 60~100 cm)共采集45个土壤样品, 测定了土壤可见光-近红外反射光谱和10种土壤理化属性, 研究了偏最小二乘和随机森林两种方法的预测能力, 分析了不同光谱变换形式对预测精度的影响, 探讨了入侵年限和土壤深度作为辅助预测变量的潜力。结果表明: (1)可见光-近红外光谱技术可以较好地预测有机碳、 无机碳、 全氮、 含水量、 pH、 容重、 盐分和黏粒等属性; (2)偏最小二乘回归法比随机森林法更适合监测互花米草入侵湿地的关键土壤理化属性, 利用偏最小二乘法对土壤属性建立的预测模型精度(R2)在 0.341~0.979之间, 随机森林方法对土壤属性建立的预测模型精度(R2)最高为0.722; (3)基于原始光谱可以获得土壤全氮的最优预测模型(R2为0.769, RMSE为0.091 g·kg-1), 而其他土壤属性的最优模型多是基于微分变换或倒数变换建立的模型, 微分变换和倒数变换可以有效地提高模型预测精度; (4)模型预测精度在加入入侵年限和土壤深度两个变量后总体上有所提高, 其中有机碳、 全氮、 盐分、 pH和容重等属性的预测精度对这两个变量更为敏感, 土壤有机碳最优模型的精度(R2)从0.794提高到0.806, pH最优模型的精度(R2)从0.838提升至0.884, 盐分最优模型的精度(R2)从0.978提升至0.997。综上所述, 可见光-近红外光谱技术在互花米草入侵湿地关键土壤理化属性预测方面具有明显的优越性, 通过适当的光谱变换、 变量筛选、 模型选择等方面可以实现互花米草入侵湿地土壤变化的快速监测。

关键词: 互花米草入侵; 可见光-近红外光谱; 土壤监测; 偏最小二乘法; 随机森林; 光谱变换
中图分类号:S153.6 文献标志码:A
Using Spectroscopy to Predict Soil Properties on Coastal Wetlands Invaded by Spartina Alterniflora
CHEN Xu, CAO Si-heng, YANG Ren-min, CHEN Qiu-yu, LI Jian-guo, XU Lu*
School of Geography, Geomatics and Planning, Department of Geographic Information Science, Jiangsu Normal University, Xuzhou 221116, China
*Corresponding author
Abstract

This study aimed to effectively monitor the changes in soil properties after Spartina alterniflora invasion on coastal wetland ecosystems. The study area is a typical Spartina alterniflora wetland in the Yancheng Wetland Rare Birds National Nature Reserve of Jiangsu Province. A total of 15 sites were identified by a stratified-random sampling method, and 45 soil samples were collected from three depth intervals (0~30, 30~60, and 60~100 cm). The visible-near infrared spectral reflectance and 10 soil physicochemical properties were measured. The performance of partial least squares regression (PLSR) and random forest (RF) was studied, spectral transformation forms’ influence on prediction accuracy was analyzed, and the potential of invasion years and soil depth as auxiliary predictors were discussed. The results show that: (1) the visible-near infrared spectral reflectance can be used to predict organic carbon, inorganic carbon, total nitrogen, water content, pH, bulk density, salinity, and clay contents in soils with reasonable accuracy; (2) the method of partial least squares generally outperform random forest algorithm, the R2 of prediction models developed using the PLSR method was between 0.341 and 0.979, and the biggest R2 of random forest models was 0.722; (3) Differential transformation and reciprocal transformation of spectral reflectance can substantially improve the model performance. The optimal prediction model of full nitrogen can be obtained based on the original spectra (R2 is 0.769 and RMSE is 0.091 g·kg-1). In contrast, the optimal models for other soil properties are mostly based on differential or reciprocal transformation of the original spectra. (4) In general, the model performance can be improved by adding variables of invasion years and soil depth, and the prediction accuracy of organic carbon, total nitrogen, salinity, pH and bulk density models are more sensitive to the two variables. The prediction model accuracy (R2) for estimating soil organic carbonincreased from 0.794 to 0.806, the accuracy (R2) of the pH model increased from 0.838 to 0.884, and the accuracy (R2) of the salt optimal model increased from 0.978 to 0.997. To sum up, visible-near infrared spectroscopy can be applied to predict key soil physicochemical properties in Spartina alterniflora wetlands, and soil change monitoring of invaded Spartina alterniflora wetlands can be achieved through appropriate spectral transformation, and variable selection and model selection.

Keyword: Spartina alterniflora invasion; Visible-near infrared spectroscopy; Soil monitoring; Partial least squares regression; Random forest; Spectral transformation
引言

在过去的40年中, 互花米草广泛地入侵了我国海岸带湿地生态系统, 对滨海湿地土壤产生了重要影响[1]。有研究表明, 互花米草生长周期较长, 拥有更高的净光合作用速率, 可以产生较大的净初级生产力, 有利于提高滨海湿地的土壤固碳能力[2]。互花米草入侵光滩和草本植物滩涂后, 可以促进湿地土壤氮的累积, 提高土壤的磷含量和微生物酶活性[3]。土壤理化性质的变化对土壤碳循环和温室气体排放有重要影响[4]。因此, 快速、 高效地监测互花米草入侵对滨海湿地土壤属性的影响, 在湿地土壤生态系统保护和管理工程中具有重要的科学和实践价值。

传统的土壤变化监测往往依赖于野外调查获取一定规模的土壤数据, 这通常耗费大量的人力、 物力和时间。高光谱技术具有方便、 无损等优点, 被广泛应用于土壤属性预测研究[5]。可见光-近红外光谱的不同波谱范围可以反映特定土壤属性的差异, 在土壤属性定量预测研究中发挥着重要作用[6]。在利用高光谱数据构建土壤属性预测模型的众多方法中, 偏最小二乘法和随机森林法是较常用的两种方法。翁永玲等发现利用高光谱数据和偏最小二乘法定量预测土壤盐分含量时具有较好的优越性和普适性[7]。Zhao等采用偏最小二乘回归和支持向量机等模型对土壤中钙离子、 镁离子、 钾离子、 钠离子含量进行预测与对比, 结果显示偏最小二乘回归建立起的地表土壤阳离子交换量预测模型对钙离子与镁离子的预测效果最高(R2分别为0.81和0.85)[8]。Seema等利用可见光近红外光谱建立偏最小二乘回归预测模型对恒河平原中部地区土壤有机碳进行预测(最优模型的R2达到0.73, RMSE为0.07%, RPD为1.9), 表明可见光近红外光谱在土壤有机碳快速评估与检测方面的潜力[9]。Nawar等利用VIS-NIR光谱技术和随机森林算法对土壤有机碳进行在线预测, 研究认为模型预测性能取决于所使用的数据集, 室内监测比在线预测有更高的精度[10]。Lin等制备了一系列不同含水量的土壤全氮混合物, 并在室内获取VIS-NIR光谱数据, 利用混合的权重学习-随机森林模型预测土壤总氮含量, 并取得较好的效果[11]。由此可知, 可见光-近红外光谱技术被广泛应用于土壤属性的预测研究中, 运用各种建模方法(偏最小二乘、 随机森林模型和支持向量机等)寻找土壤属性的最优预测模型成为主要研究目标。本研究建立了偏最小二乘和随机森林两种方法土壤属性预测模型, 探究两种模型方法对土壤关键属性的预测能力。

已有研究表明, 光谱变换可以放大光谱反射或吸收特征, 提高土壤属性预测模型的稳定性和预测精度[12, 13]。例如, 光谱数据进行微分处理, 不仅可以去除背景噪声, 还可以去除基线, 辨别出重叠峰, 从而突出光谱细节特征, 一阶微分处理可以清除一次方项的噪声, 二阶微分处理可以清除平方项的噪声[14]。张贤龙等在研究中发现基于光谱一阶微分和倒数对数变换后土壤盐分的预测效果较好[15]。Stevens等发现经过导数变换和平滑处理后建立的土壤有机质预测模型精度得到提高[16]。朱赟等基于不同光谱变换方法对土壤盐分含量进行反演, 发现倒数变换可以显著提高模型预测精度[17]。对光谱数据进行数学变换可以有效提高土壤属性预测模型精度, 本研究对光谱数据进行倒数变换和微分变换以及二者的组合的预处理手段, 以达到提高关键土壤属性预测模型精度的的目的。

江苏盐城互花米草入侵湿地为研究区, 以高效监测互花米草入侵海岸带湿地生态系统的土壤属性变化为目标展开研究。研究从三个角度为切入展开: (1)研究偏最小二乘和随机森林两种建模方法对关键土壤属性的预测能力; (2)分析不同光谱变换形式对模型精度的影响; (3)探讨入侵年限和土壤深度作为辅助预测变量的潜力。

1 实验部分
1.1 研究区概况

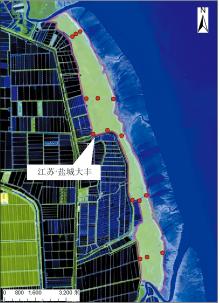
研究区位于江苏省盐城湿地珍禽国家级自然保护区典型互花米草入侵湿地, 经纬度范围为33° 20'N—33° 30'N和120° 40'E—120° 45'E, 东临黄海, 背靠苏北平原, 呈条带状分布(图1)。该研究区位于温带和亚热带之间, 年平均气温12~21 ℃, 降水量集中在6月到9月, 年平均降水量为1 023.16 mm, 属于典型的亚热带季风气候[1]。

图1 研究区位置及采样点分布图Fig.1 Map of study area and sampling sites

1.2 土壤样品采集与土壤属性测定

利用分层随机采样法布设15个样点, 分布在5条海向样带(如图1所示)。首先使用目视解译方法从Landsat时间序列数据中提取2000年、 2004年、 2010年和2016年的互花米草入侵边界信息, 然后依据道路通达性选取5条海向样带, 在每条样带兼顾互花米草入侵阶段特性的同时随机布设样点, 再次利用目视解译法从Landsat时间序列数据中提取每个样点的互花米草入侵年限信息[18]。野外调查工作于2017年开展, 在每个样点深挖1 m深度的土壤剖面, 划分3个层次(0~30、 30~60和60~100 cm), 共采集45组土壤样品, 每组样品包含用于分析基本土壤属性的混合样和用于测定土壤容重的环刀样。

将采集的45组土壤样品进行晾干并过筛, 分析十种土壤物理和化学属性。土壤有机碳含量(SOC, g· kg-1)通过Walkley-Black湿式燃烧法分析。无机碳含量(SIC, g· kg-1)用土壤中的碳酸盐含量表示。盐分含量(SC, g· kg-1)通过导电率和干蒸发率法测定。pH值在土水比为1∶ 2.5的溶液中测量。土壤容重(BD, g· cm-3)通过直径5 cm、 深度5 cm的岩心土壤样品的干重/总土壤体积测定[19]。土壤含水量(WC, %)采用传统的烘干法测量。通过凯氏消化程序分析总氮浓度(TN, g· kg-1)[20]。土壤颗粒大小通过马尔文土壤颗粒激光粒度仪器分析。以上土壤物理化学属性测定参考[1, 18]。

1.3 土壤光谱的测定与预处理

利用ASD FieldSpec 3便携式地物波谱仪提取出土壤光谱反射率, 波谱范围为350~2 500 nm, 采样间隔为1.4 nm(350~1 000 nm)和2 nm(1 000~2 500 nm), 重采样间隔为1 nm。光谱采集在暗室中进行, 首先将直径5 cm、 深度2 cm的容器装满土样并刮平表面, 然后选用功率为50 W的卤素灯作为光源, 放置在距离样本中心约30 cm, 入射角为45° 。光纤探头视场角设置为8° , 垂直放置在土样正上方15 cm处。在测量土壤光谱前需进行白板矫正, 测量过程中每个样品测5次, 取算术平均值作为该土壤样品的光谱反射率。

为突出土壤光谱特征, 对土壤原始光谱进行了去噪和降维等预处理[2]。首先利用Savitzky-Golay卷积平滑法降噪, 然后对光谱数据重采样, 降低数据维度, 重采样间隔设置为10 nm, 共获取216个波段。为了探讨光谱变换对模型精度的影响, 本研究获取了原始光谱、 倒数、 一阶微分、 二阶微分、 倒数的一阶微分和倒数的二阶微分等六种不同的光谱变换数据, 光谱变换形式如表1所示。

表1 土壤光谱数学变换形式 Table 1 Mathematical transformation forms of the soil spectrum
1.4 时空辅助变量

研究区位于我国东部的沿海湿地, 该地区土壤功能在很大程度上受互花米草入侵的影响, 在互花米草入侵年限尺度和土壤深度尺度上表现出较强的规律性和异质性。因此, 把互花米草入侵年限和土壤采样深度作为时空辅助变量参与土壤属性的建模, 在一定程度上可以提高土壤属性预测模型的精度[2]。

1.5 研究方法

为了探究土壤属性在时间尺度的变化规律, 采用相关性分析方法研究了土壤属性与入侵年限之间的关系。进一步采用偏最小二乘和随机森林法, 分别以六种光谱变换形式为自变量, 考虑互花米草入侵年限和土壤采样深度作为辅助预测变量对土壤属性预测的潜在影响, 分别建立10种土壤属性的预测模型, 对比分析不同建模条件对土壤属性预测模型精度的影响。对每个土壤属性建立24个预测模型(2种建模方法× 6种光谱变换× 有无辅助变量)。

偏最小二乘法(PLSR)建模的优越为, 建模过程中引入潜在空间, 把原始数据投影到潜在空间中, 利用正交结构提取潜在变量, 找出潜在变量和因变量之间的关系, 最后采用留一法交叉验证确定潜在变量的个数, 建立偏最小二乘法回归模型[21]。随机森林(RF)的本质是利用Bootstrap重采样方法从原始数据中抽取若干样本, 对每个Bootstrap样本进行决策树建模, 结合多棵子决策树的预测, 通过投票得出最终预测结果[9]。

1.6 模型验证和评价

采用留一交叉验证法评价土壤属性的预测效果, 即每次分别从三个土壤深度中随机选取一个样本作为验证数据集, 其余样本作为建模数据集, 直到所有样品均参与了模型验证。模型预测精度采用决定系数(R2)和均方根误差(RMSE)两个参数评价。R2反映模型的拟合效果, R2越接近1, 表明预测值与实测值之间的匹配程度越高。RMSE用于衡量模型的预测误差, 该参数数值越小, 表明模型的预测精度越高。

R2=1-∑i=1n(y-y^i)2∑i=1n(yi-y̅)2(1)

RMSE=∑i=1n(yi-y^i)2n(2)

式(1)和式(2)中, y^i为预测值, yi为实测值, y̅为实测平均值, n为建模集样本数量。

2 结果与讨论
2.1 互花米草入侵湿地的土壤光谱特征

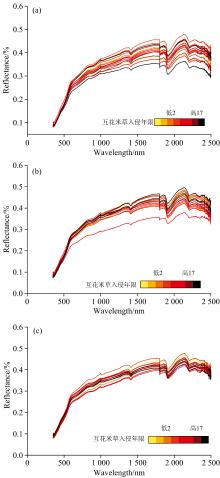
图2(a, b, c)分别为三个不同深度的土壤光谱反射率曲线, 研究区土壤样本的光谱曲线形态基本一致, 为曲折式上升的抛物线型, 在1 400、 1 900和2 200 nm有较明显的水分吸收谷。在可见光波段范围(350~760 nm), 不同深度的光谱反射曲线整体上呈现陡峭的上升趋势, 各样本曲线间差异较小; 近红外波段区间内(760~2 500 nm), 不同深度的光谱反射率更为平缓, 而样本间的光谱差异更大。不同入侵阶段的土壤光谱曲线存在差异, 但规律不明显。不同采样深度的光谱反射率曲线形态基本一致, 随着深度的增加土壤光谱反射率差异逐渐减小。

图2 不同深度土壤光谱反射率曲线
(a): 表层土壤(0~30 cm); (b): 中层土壤(30~60 cm); (c): 深层土壤(60~100 cm)Fig.2 Soil spectral reflectance curves at different depths
(a): Top soil (0~30 cm); (b): Sub soil (30~60 cm); (c): Bottom soil (60~100 cm)

2.2 土壤属性在空间尺度上的变化特征

对土壤理化属性(表2)进行描述性统计分析, 发现: (1)在深度上土壤有机碳和全氮分布特征相似, 即随着深度增加属性值降低, 其中有机碳均值从7.37 g· kg-1降至4.39 g· kg-1, 全氮均值从0.62 g· kg-1降为0.39 g· kg-1; (2)土壤盐分、 含水量和容重在深度上呈现出先递增再降低或先降低再递增的特点, 其中盐分均值从10.24 g· kg-1增至10.66 g· kg-1再降至9.33 g· kg-1, 容重均值从1.25 g· cm-3降至1.21 g· cm-3再增至1.28 g· cm-3, 含水量均值从39.74%增至46.51%再降至43.39%; (3)无机碳、 pH、 黏粒、 粉粒、 砂粒在深度上未表现出明显的变化规律, 它们在1 m深度内的均值分别为11.57 g· kg-1、 8.59、 13.02%、 68.23%、 18.75%。

表2 土壤理化属性描述性统计 Table 2 Descriptive statistics of soil physical and chemical properties
2.3 土壤属性在时间尺度上的变化特征

土壤属性与入侵年限的相关性分析结果(表3)可以看出: (1)在三个深度, 土壤有机碳、 全氮、 pH均与入侵年限呈正相关关系, 且仅在表层30 cm深度表现出显著相关; (2)土壤盐分在三个深度均与入侵年限呈显著负相关关系; (3)土壤容重与入侵年限的关系仅在表层30 cm深度显著, 为正相关关系; (4)无机碳、 含水量、 黏粒、 粉粒、 砂粒与互花米草的入侵年限之间不存在变化规律。

表3 土壤理化属性与入侵年限增加的相关性 Table 3 Correlation between soil physicochemical properties and increased invasion years
2.4 土壤属性预测与精度评价

除粉粒和砂粒外, 偏最小二乘法对其他8种土壤属性的预测精度普遍优于随机森林模型(图3)。采用偏最小二乘法对土壤属性建立的预测模型的R2在0.341~0.979之间, RMSE在0.048~7.679之间; 随机森林对土壤属性建立的预测模型的R2在0~0.722之间, RMSE范围在0.110~9.720之间。

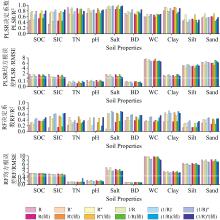图3 不同建模变量的偏最小二乘法和随机森林方法预测土壤属性Fig.3 Predicting soil properties using PLSR and RF based on different variables

研究结果表明, 光谱数学变换对预测精度有较大影响, 不同土壤属性的最优预测模型所需的光谱数学变换存在差异。基于原始光谱可以获得全氮的最优预测模型(R2为0.769, RMSE为0.091 g· kg-1), 而其他土壤属性的最优模型多为基于微分变换或倒数变换建立的模型。其中, 基于二阶微分变换的光谱数据可以获得土壤有机碳(最优模型R2为0.806, RMSE为0.913 g· kg-1)、 粉粒(最优模型R2为0.490, RMSE为4.993%)和砂粒(最优模型R2为0.577, RMSE为6.255%)的最优模型, 基于倒数变换的光谱数据可以获得土壤无机碳(最优模型R2为0.702, RMSE为0.615 g· kg-1)、 盐分(最优模型的R2为0.839, RMSE为1.760 g· kg-1)、 容重(最优模型R2为0.689, RMSE为0.095 g· cm-3)和含水量(最优模型的R2为0.803, RMSE为8.456%)的最优模型, 基于一阶变换的光谱数据可以获得pH(最优模型的R2为0.889, RMSE为0.074)和黏粒(最优模型的R2为0.839, RMSE为1.76%)的最优模型。因此对于多数土壤属性, 恰当的土壤光谱数学变换有助于提高预测精度。

在模型中加入辅助变量对不同土壤属性的预测精度有不同程度的影响。在偏最小二乘法模型中加入入侵年限和采样深度两个辅助变量后, 土壤有机碳、 pH和盐分的预测精度得到了明显提高: 土壤有机碳最优模型的R2从0.794提高到0.806, pH最优模型的R2从0.838提升至0.884, 盐分最优模型的R2从0.978提升至0.997。在随机森林建模过程中, 除pH值、 砂粒和容重在加入辅助变量后预测精度降低, 对其余土壤属性的预测在建模时加入辅助变量后预测精度均有一定程度的提高, 分析认为辅助变量对pH值、 砂粒和容重的影响较小。

研究表明, 可见光-近红外光谱技术在预测互花米草入侵湿地的关键土壤理化属性方面具有显著优势。Yang等利用SEM模型成功地预测三个深度的有机碳(RMSE=1.63 g· kg-1, RPD=1.22)和容重(RMSE=0.14 g· cm-3, RPD=1.25)[22]。陈秋宇等基于VIS-NIR光谱技术利用偏最小二乘法预测土壤有机碳含量, 最优预测模型的R2=0.68, RMSE=1.31 g· kg-1[2]。有研究基于单一的模型预测方法、 对少量的土壤属性进行建模预测, 而本研究考虑到多种土壤关键属性, 并对比偏最小二乘和随机森林两种预测方法的优劣, 发现偏最小二乘法更适合监测互花米草入侵湿地的土壤属性变化过程, 其中有机碳(最优模型R2为0.806, RMSE为0.913 g· kg-1)、 盐分(最优模型的R2为0.839, RMSE为1.760 g· kg-1)和黏粒(最优模型的R2为0.839, RMSE为1.76%)预测效果最佳。有研究将偏最小二乘回归与GBDT相结合应用于LUCAS数据库, 同时对林地、 草地和耕地三种类别土壤的有机碳、 氮、 粘土含量进行了预测(不同特征提取方法下R2分别在0.658~0.679、 0.687~0.719、 0.739~0.812范围内)[23]。Nawar等利用可见光近红外波段对比建立起多元自适应样条回归模型, 对埃及西奈北部地区土壤的有机质与盐分含量进行了预测, R2分别达到0.81与0.79, 同时提出多元自适应样条回归方法在推广到大面积土壤检测具备优势[10]。Yang等使用近红外和偏最小二乘法分析预测全球土壤质量指数(SQI), SQI在该波段范围内存在明显的光谱差异, 进一步证实了近红外光谱技术在监测互花米草入侵湿地土壤质量方面具有很大的潜力[5]。本研究采用可见光和近红外技术对湿地土壤的几种关键属性进行预测, 取得了较好的预测成果。在互花米草入侵湿地的大背景下, 选择适宜的预测方法, 利用可见光和近红外光谱技术, 可以高效监测土壤属性变化情况。

通过对比基于不同光谱变换形式建立的预测模型, 发现微分变换和倒数变换可以提高大多数土壤属性的预测精度。有研究表明, 一阶微分可以移除基线常量的影响, 二阶微分可以保留原始特征峰, 可以更方便地解译土壤光谱; 倒数变换可以实现某些非线性关系到线性关系的转换, 更简洁、 直观地解译光谱反射率与土壤属性的关系[14]。Nawar等对多种光谱变换方法进行对比, 结果表明一阶微分变换结合SG平滑、 连续统去除可以有效提升偏最小二乘回归模型、 支持向量机模型、 多元自适应样条回归模型的预测能力[13]。朱赟等的研究表明光谱变换可以突出与放大光谱特征, 倒数对数结合二阶微分变换与SG平滑显著提升了光谱特征和盐含量之间的相关性以及模型预测精度[17]。针对不同的土壤属性, 在建模前对光谱反射率进行适当的变化可以提升模型的预测精度。

模型预测精度在加入入侵年限和土壤深度两个变量后可以得到提高, 其中有机碳、 全氮、 盐分、 pH和容重等属性的预测精度对这两个变量更为敏感。分析认为互花米草入侵海岸带湿地生态系统后, 土壤属性受到了环境因子、 物种特性、 入侵年限等因素的共同作用[20]。研究区位于我国东部的沿海湿地, 受米草入侵和海水侵蚀的影响, 土壤属性受时空变量的影响较大, 在时间和空间上存在明显的变化规律。有研究表明, 在利用近地传感技术预测互花米草入侵湿地土壤有机碳时加入辅助变量建立的混合变量模型精度更高[2]。

在互花米草入侵湿地, 偏最小二乘法相对于随机森林能够更好地预测关键土壤理化属性。Zhao等在对土壤阳离子的预测过程中发现PLSR比RF和Cubist法的预测效果更好, 可以较好地预测土壤盐分含量[8]。Seema等在研究中发现偏最小二乘法和随机森林对恒河平原的土壤有机碳建立的模型均具有较好的预测效果, 偏最小二乘法(R2=0.730, RMSE=0.07%)比随机森林法(R2=0.690, RMSE=0.07%)预测精度略高一点[9]。Liu等的研究表明, 偏最小二乘法可以有效降低光谱数据维度并且尽可能保留与目标相关的信息[21]。本研究区为典型的外来植被入侵的滨海湿地, 使用偏最小二乘法方法可以有效地解决变量间的多重线性问题, 使模型具有较高稳定性和预测能力。随机森林法擅长处理非线性关系, 但需要大量的数据作为支撑, 本研究土壤样本数量较少, 随机森林预测模型精度存在一定的误差。因此, 研究区内偏最小二乘法比随机森林法更适合预测湿地土壤属性。

3 结论

针对互花米草入侵湿地关键土壤理化属性变化的高效监测, 基于可见光-近红外光谱技术, 探讨了建模方法、 土壤光谱变换形式、 以及辅助变量选择等方面对土壤属性预测的影响。相关结论:

(1)土壤有机碳、 盐分、 全氮、 pH和容重受互花米草入侵的影响最为明显。互花米草的入侵可显著增加表层30 cm的土壤有机碳、 全氮、 pH和容重, 而显著降低1 m土体内的盐分含量。

(2)可见光-近红外光谱在预测互花米草入侵湿地的关键土壤理化属性方面具有显著优势。对于多数土壤属性, 基于微分变换或倒数变换的光谱数据建立的预测模型具有更高的预测精度。

(3)加入时空辅助变量建立的预测模型比单一的基于土壤光谱建立的预测模型精度更高。有机碳、 全氮、 盐分、 pH和容重等属性的预测精度对这两个变量更为敏感, 土壤有机碳最优模型的精度(R2)从0.794提高到0.806, pH最优模型的精度(R2)从0.838提升至0.884, 盐分最优模型的精度(R2)从0.978提升至0.997。

(4)偏最小二乘法(模型精度R2在0.341~0.979之间)比随机森林(模型精度R2最高为0.722)更适合用于监测互花米草入侵湿地的关键土壤理化属性。

参考文献
[1] Yang Renmin, Guo Wenwen. Soil Science Society of America Journal, 2018, 82(4): 901. [本文引用:3]
[2] CHEN Qiu-yu, YANG Ren-min, ZHU Chang-ming(陈秋宇, 杨仁敏, 朱长明). Acta Pedologica Sinica(土壤学报), 2021, 58(3): 694. [本文引用:5]
[3] Anna Christina Tyler, John G Lambrinos, Edwin D Grosholz. Ecological Applications, 2007, 17(7): 1886. [本文引用:1]
[4] LIU Zi-gang(刘子刚). Scientia Geographica Sinica(地理科学), 2004, 24(5): 634. [本文引用:1]
[5] Yang Renmin, Wang Liangjie, Chen Liumei, et al. Environmental Earth Sciences, 2022, 81: 19. [本文引用:2]
[6] ZHANG Wen-juan, WANG Shao-qiang, CHANG Hua, et al(张文娟, 王绍强, 常华, 等). Progress in Geography(地理科学进展), 2005, (3): 118. [本文引用:1]
[7] WENG Yong-ling, QI Hao-ping, FANG Hong-bin, et al(翁永玲, 戚浩平, 方洪宾, 等). Acta Pedologica Sinica(土壤学报), 2010, 47(6): 1255. [本文引用:1]
[8] Zhao Dongxue, Maryem Arshad, Wang Jie, et al. Computers and Electronics in Agriculture, 2021, 182: 105990. [本文引用:2]
[9] Seema, Ghosh A K, Das B S, et al. Geoderma Regional, 2020, 23: e00349. [本文引用:3]
[10] Nawar S, Mouazen A M. Soil and Tillage Research, 2019, 190: 120. [本文引用:2]
[11] Lin Lixin, Liu Xixi. Computers and Electronics in Agriculture, 2022, 192: 106634. [本文引用:1]
[12] WANG Miao, XIE Xian-li, ZHOU Rui, et al(王淼, 解宪丽, 周睿, 等). Acta Pedologica Sinica(土壤学报), 2011, 48(5): 1083. [本文引用:1]
[13] Said Nawar, Henning Buddenbaum, Joachim Hill, et al. Soil & Tillage Research, 2016, 155: 510. [本文引用:2]
[14] Arve J Iversen, Torgny Palm. Applied Spectroscopy, 1985, 39(4): 641. [本文引用:2]
[15] ZHANG Xian-long, ZHANG Fei, ZHANG Hai-wei, et al(张贤龙, 张飞, 张海威, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2018, 34(1): 110. [本文引用:1]
[16] Antoine Stevens, Thomas Udelhoven, Antoine Denis, et al. Geoderma, 2010, 158(1): 32. [本文引用:1]
[17] ZHU Yun, SHEN Guang-rong, XIANG Qiao-qiao, et al(朱赟, 申广荣, 项巧巧, 等). Chinese Journal of Soil Science(土壤通报), 2017, 48(3): 560. [本文引用:2]
[18] SUN Yue-qi, SUN Xiao-mei, WU Zhen-fu, et al(孙越琦, 孙笑梅, 巫振富, 等). Acta Pedologica Sinica(土壤学报), 2023, 60(6): 1595. [本文引用:2]
[19] YU Dong-xue, JIA Xiao-xu, HUANG Lai-ming, et al(于冬雪, 贾小旭, 黄来明, 等). Acta Pedologica Sinica(土壤学报), 2019, 56(1): 55. [本文引用:1]
[20] MA Yu-ying, LEI Ting-wu, ZHANG Xin-ping, et al(马玉莹, 雷廷武, 张心平, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2013, 29(9): 86. [本文引用:2]
[21] Liu Lanfa, Ji Min, Manfred Buchroithner. Remote Sensing, 2017, 9(12): 1299. [本文引用:2]
[22] Yang Renmin, Guo Wenwen. International Journal of Applied Earth Observation and Geoinformation, 2019, 82: 101906. [本文引用:1]
[23] QIU Yue-feng, YANG Chao, LIN Fen-fang, et al(邱乐丰, 杨超, 林芬芳, 等). Chinese Journal of Applied Ecology(应用生态学报), 2010, 21(12): 3099. [本文引用:1]