引用本文
李昊天, 李发泉, 李娟, 王后茂, 武魁军, 何微微. 光稀释效应对O2近红外气辉星载测风的影响 [J]. 光谱学与光谱分析, 2025,45(1): 160-169.
LI Hao-tian, LI Fa-quan, LI Juan, WANG Hou-mao, WU Kui-jun, HE Wei-wei. The Influence of Optical Dilution Effect for Spaceborne Wind Measurement on O2 Near Infrared Airglow [J]. Spectroscopy and Spectral Analysis, 2025,45(1): 160-169.
Doi:10.3964/j.issn.1000-0593(2025)01-0160-10  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
光稀释效应对O2近红外气辉星载测风的影响
李昊天1, 李发泉2, 李娟3, 王后茂4, 武魁军1, 何微微1,*
1.烟台大学物理与电子信息学院, 山东 烟台 264005
2.中国科学院精密测量科学与技术创新研究院, 湖北 武汉 430071
3.中国科学院西安光学精密机械研究所, 陕西 西安 710119
4.中国科学院国家空间科学中心, 北京 100190
*通讯作者 e-mail: heweiwei@ytu.edu.cn

作者简介: 李昊天, 1999年生, 烟台大学物理与电子信息学院硕士研究生 e-mail: lihaotian@s.ytu.edu.cn

收稿日期: 2023-12-18 修订日期: 2024-03-18
基金: 国家自然科学基金项目(62305283, 41975039), 山东省自然科学基金项目(ZR2021QD088), 山东省高等学校“青创科技支持计划”项目(2021KJ008), 烟台大学研究生科研创新基金(GGIFYTU2418)资助
摘要

利用星载光谱成像干涉仪测量O2(a1Δg)日辉的多普勒频移信息是目前实现全球临近空间大气风场探测的先进技术手段, 观测谱线O19P18(7 772.030 cm-1)的多普勒频移, 可以在40~80 km的空间区域进行高精度和高灵敏度的风速测量, 然而其探测精度受大气散射的具体影响尚不明晰。文章旨在分析光稀释效应对临近空间大气风场探测的影响, 并对其引起的测风误差进行定量评估。首先介绍了O2(a1Δg)光谱和大气散射的光谱特性。采用最新的HITRAN光谱参数、 光化学反应速率常数以及大气模型计算得到O2(a1Δg)不同反应机制的贡献。结合光化学反应速率计算得到O2(a1Δg)的体辐射率, 并分析了太阳天顶角对体辐射率分布的影响, 基于爱因斯坦系数和谱线强度分别计算得到O2(a1Δg)在不同温度和自吸收效应条件下的光谱辐射模型, 并分析了不同地理气象因素对大气散射光谱造成的影响。其次, 介绍了临边观测多普勒非对称空间外差光谱仪(DASH)的测量技术原理, 描述了如何去除大气散射分量以生成纯净的气辉干涉图, 基于DASH仪器概念对获取干涉图像的正演过程进行了阐释。再次, 针对反演问题引入了“剥洋葱算法”, 在考虑自吸收效应和光稀释效应影响的情况下, 消除了目标层上方大气层贡献, 解决了干涉图像中目标层信息的提取问题。最后, 通过误差分析得到了大气风场探测精度廓线及其随地理气象因素影响的变化规律, 证明光稀释效应的存在降低了干涉图对比度并增加了测量噪声, 这对临边观测权重和有效信噪比产生了不利影响。研究表明, 在45~80 km的切线高度范围内, 测风精度受大气散射的影响较小, 其误差约为2~3 m·s-1; 而在45 km以下, 测风精度受光稀释效应的影响随海拔高度的降低而急剧增大, 且受地表反照率、 气溶胶和云量等因素的影响而显著升高, 在同时考虑三种因素影响的情况下, 其探测下限最低约为40 km。

关键词: 临近空间; 光稀释效应; 测量精度; 大气风场; 光学仪器
中图分类号:P356 文献标志码:A
The Influence of Optical Dilution Effect for Spaceborne Wind Measurement on O2 Near Infrared Airglow
LI Hao-tian1, LI Fa-quan2, LI Juan3, WANG Hou-mao4, WU Kui-jun1, HE Wei-wei1,*
1. College of Physics and Electronic Information, Yantai University, Yantai 264005, China
2. Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China
3. Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China
4. National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China
*Corresponding author
Abstract

Measurement of the Doppler shift information of the O2(a1Δg) day glow using the satellite-borne spectral imaging interferometer is currently the state-of-the-art technological means to realize the detection of the atmospheric wind field in the global adjacent space. Observing the Doppler shift of the spectral line O19P18 (7 772.030 cm-1) allows high-precision and high-sensitivity wind speed measurements in the 40~80 km spatial region. However, the specific effect of atmospheric scattering on its detection precision is unknown. This paper aims to quantitatively assess wind measurement errors due to the optical dilution effect. First, the spectral properties of the O2(a1Δg) spectrum and the atmospheric scattering spectrum are introduced. The contributions of different reaction mechanisms of O2(a1Δg) were calculated using the latest HITRAN spectral parameters, photochemical reaction rate constants, and NRLMSIS 2020. The volume emission rate (VER) of O2(a1Δg) was calculated based on the photochemical reaction rate, and the effect of the solar zenith angle on the VER distribution was analyzed. Spectral radiation models of O2(a1Δg) at different temperatures and self-absorption effects were obtained based on the Einstein coefficient and spectral line intensity, respectively. The effects of different geographical and meteorological factors on the atmospheric scattering spectrum were also analyzed. Secondly, the principles of the measurement technique of the Doppler Asymmetric Spatial Heterodyne spectroscopy (DASH) for limb-viewing are introduced. Describes removing the atmospheric scattering component to produce a pure airglow interferogram. The forward process for acquiring interferometric images is explained based on the DASH instrument concept. Thirdly, the “onion peeling” algorithm was introduced for the retrieval problem. The contribution of the atmosphere above the target layer is eliminated while considering the influence of the self-absorption and optical dilution effects. The problem of extracting target layer information in interferometric images is solved. Finally, the atmospheric wind field detection precision profiles and their changing laws with the influence of geographical and meteorological factors are obtained by error analysis. It is demonstrated that the optical dilution effect reduces the interferogram visibility and increases the measurement noise, adversely affecting the limb-viewing weights and the effective signal-to-noise ratio. In the tangent altitude range of 45~80 km, the wind measurement precision is less affected by atmospheric scattering, with an error of about 2~3 m·s-1. Below 45 km, the wind measurement precision is affected by the optical dilution effect that increases sharply with decreasing altitude and is significantly increased by the surface albedo, aerosol, and cloud. When the effects of all three factors are considered simultaneously, the minimum lower detection limit is about 40 km.

Keyword: Near space; Optical dilution effect; Measurement precision; Atmospheric wind; Optical instrument
引言

临近空间是指位于航空和航天飞行器运行轨道高度之间的区域, 其覆盖范围大约在20~120 km之间, 跨越平流层、 中间层及一部分热层, 因其处于空天衔接处, 因此是航空航天技术未来发展的重点领域[1]。大气风场是表征临近空间环境状态的重要参量之一, 精确探测全球尺度的临近空间大气风场三维分布对研究大气能量传输和成分运输以及大气环流特性具有重要的学术研究意义, 而且对提高数值天气的预测精准度, 保证航天飞行器安全入轨具有重要的应用价值[2]。

由于技术手段的限制导致临近空间大气风场探测数据相较于其他海拔高度较为缺乏。传统的测风手段主要有: 多普勒激光雷达[3]等地基遥感探测方式[4]以及探空气球[5]、 气象火箭[6]等空基原位探测方式。但上述测风手段在高度覆盖或时间、 空间分辨率方面受到极大制约, 难以获得全球临近空间风场的分布情况。

空间技术的不断发展使得星载测风成为可能。星载激光雷达或星载气辉成像干涉仪能够通过探测谱线的频移信息, 实现全球尺度的大气风场探测, 现已逐渐成为大气风温探测领域的前沿课题。2018年, 欧空局发射的风神卫星(atmospheric dynamics mission, ADM-Aeolus)上搭载的多普勒测风激光雷达, 成功测量并获得了对流层至平流层底部(0~30 km)的全球大气风廓线[7]。2019年, 美国NASA发射的电离层连接探测器(ionospheric connection explorer, ICON)上搭载的全球高分辨率热层成像迈克尔逊干涉仪(Michelson interferometer for global high-resolution thermospheric imaging, MIGHTI), 通过观测氧原子的绿线气辉(557.7 nm)和红线气辉(630.0 nm)的多普勒频移实现了对90~300 km热层中性风的全球遥感[8]。

然而, 对于30~90 km处的临近空间区域, 目前尚无有效卫星载荷可实现风场测量。为填补这一空白, 在加拿大航天局与地球空间技术研究中心支持下, William E Ward等开发了波迈克尔逊干涉仪(waves michelson interferometer, WAMI), 通过使用迈克尔逊干涉仪观测O2(a1Δ g)日辉的三条强发射线和三条弱发射线, 同时对45~95 km范围内的大气风场和温度场进行了测量[9]。2019年, He等对其进行了改进, 使其能够对临近空间大气风场进行全球尺度的精准探测, 且具有较高风温探测精度[10]。2018年, Wu等提出利用多普勒非对称空间外差光谱仪(doppler-asymmetric-spatial-heterodyne-spectroscopy, DASH)探测O2近红外气辉在7 772.030 cm-1的孤立谱线的多普勒频率, 以实现临近空间大气风场的探测, 该方案减少了对光谱采样间隔的设计要求, 从而大大提高了工程可行性[11]。尽管这种改进方法具有诸多优点, 然而由于其新颖性, 影响测量精度的因素尚未被完全深入研究。在众多可能影响测风精度的因素之中, 光稀释效应显然是最为关键的因素之一。

光稀释效应是指大气中的气溶胶或气体分子由于米氏散射和瑞利散射导致视线方向上部分气辉辐射出的光子被散射出相机视场外, 而部分位于相机视场外的太阳光也会被散射至相机感光面的现象。2017年, 美国伊利诺伊大学厄巴纳-香槟分校的Harding教授等首次分析了大气散射效应对地基法布里-珀罗干涉仪(Fabry-Perot interferometer, FPI)探测热层垂直风、 水平风和温度的影响, 并通过实验证明在极端情况下, 大气散射效应引起的风温探测误差分别可达400 m· s-1和200 K[12]。2018年, Wu等分析了临边观测模式下大气单次散射对星载多普勒外差干涉仪测风精度的影响, 但其采用的大气散射模型仅考虑了无云也无气溶胶的理想情况, 而对于大气的多次散射效应, 以及地表及云层反射太阳光被大气的再次散射等复杂情况并未考虑[11]。

本文针对星载DASH仪器以O2(a1Δ g)日辉为目标源进行临近空间大气风场探测, 全面深入地研究光稀释效应对探测的影响。文章对临边观测模式下O2近红外大气波段的气辉辐射光谱及大气散射光谱进行介绍; 建立DASH的仪器模型并研究其干涉图像的正演仿真方法, 进而提出解算视线(line-of-sight, LOS)积分以获得仅包含目标层信息干涉图的具体方案; 对视线风的反演算法进行介绍, 同时对DASH仪器的风速测量精度进行分析和讨论。

1 光谱概念
1.1 气辉辐射光谱

气辉指大气中处于电子激发态的分子或原子受能级寿命影响自发跃迁至基态时产生的光子辐射。

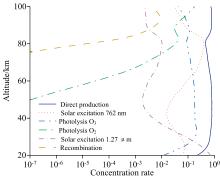
第一激发态O2(a1Δ g)分子的主要产生机理为太阳辐射的共振吸收、 O3分子光解和O(1D)的能量转移, 而其损耗机制主要是自发辐射和碰撞湮灭。O2(a1Δ g)分子的产生和损耗的光化学反应机理如图1所示。

图1 激发态O2(a1Δ g)分子的产生和损耗机理Fig.1 Generation and loss mechanism of excited state O2(a1Δ g)

以上产生机理中, 位于Hartley波段的O3的分子光解过程是产生O2(a1Δ g)气辉最重要的机理[13]。假设光化学平衡成立的条件下, 考虑与N2、 O2、 CO2、 O3、 O(3P)等基本大气成分碰撞时的猝灭过程, O2(a1Δ g)的分子数密度可由式(1)计算

nO2(a1Δg)=φαR1[O3]+∑i=15Ki[Yi][O2]{R2+ϕηR3[O(1D)]}AO2(b1Σg)+∑i=15Ki[Yi]AO2(a1Δg)+∑i=13Ci[Xi](1)

式(1)中, X={O2, N2, O}, Y={N2, O2, CO2, O3, O}, R1=8.1× 10-3, R2=5.35× 10-9, R3=3.2× 10-11exp(70/T), K1=2.1× 10-15, K2=4.2× 10-13, K3=2.2× 10-11, K4=8.0× 10-14, K5=3.9× 10-17, C1=3.6× 10-18e-220/T, C2=1.0× 10-20, 以及C3=1.3× 10-16。

综合考虑上述各种产生机制贡献得到的O2(a1Δ g)的数密度如图2所示。其中光解和光激发过程涉及的所有速率常数值均取自Yankovsky等的工作[14, 15], 跃迁概率的计算基于HITRAN 2020数据库[16], O、 O2、 N2和CO2的廓线来自NRLMSIS 2020的大气模型[17]。

图2 不同机制下对O2(a1Δ g)浓度的贡献比Fig.2 Ratio of contribution to O2(a1Δ g) concentration by different mechanisms

体辐射率(volume emission rate, VER)表示单位时间内由激发态向基态辐射的每单位体积内光子的数量, 可以通过O2(a1Δ g)的跃迁概率与其分子数密度加权计算

ηE(s)=AO2(a1Δg)·nO2(a1Δg)(s)(2)

在O2(a1Δ g)产生过程中, 除三体化学反应机制外, 其他过程受太阳辐射影响较为强烈。太阳天顶角的变化会对太阳辐射光通过吸收物质(如O2、 O3)的路径长度影响, 进而导致光化学系数和共振吸收效率变化。因此太阳天顶角的变化会影响O2(a1Δ g)的分子数密度。基于Modtran[18]获得的O3浓度廓线, 可以计算得到从0° 到90° 不同太阳天顶角(solar zenith angle, SZA)下的O2(a1Δ g) VER三维分布, 如图3所示。可以看出, O2(a1Δ g)辐射强度在正午时分达到最大, 当SZA低于50° 时, VER的峰值出现在43~45 km处。当太阳接近地平线时, 由于太阳辐射穿过的路径较长, 导致低海拔高度的O3分子的光解速率降低, 使得VER峰值随SZA增大而升高。

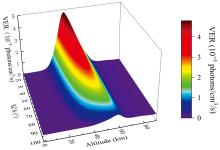图3 1.27 μ m O2(a1Δ g)气辉VER随SZA及海拔高度的变化情况Fig.3 Variation of 1.27 μ m O2(a1Δ g) airglow VER with SZA and altitude

1.27 μ m波段的O2(a1Δ g)气辉呈带状分布, 由百余条转动跃迁谱线组成, 分为R支和两个P支。O2(a1Δ g)的光谱分布取决于它们各自的旋转能级统计权重2J+1和温度T。对于转动量子数为J的跃迁谱线, 其辐射率可通过跃迁概率 AO2(a1Δg)与其配分函数Q(J, T)相乘得到

εJ=AO2(a1Δg)Q(J, T)∑Q(J, T)(3)

图4所示为不同温度下O2(a1Δ g)的辐射光谱随跃迁波长的变化情况。可以看出, 随着温度的升高, 辐射强度在谱带中心处减小, 在两翼处强度增大。

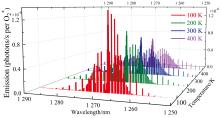图4 不同温度下O2(a1Δ g)气辉辐射光谱随跃迁波长的变化Fig.4 Variation of O2(a1Δ g) airglow radiation spectra with transition wavelength at different temperatures

对于原子气辉等不需要考虑自吸收效应的临边观测, 可将光谱辐射强度看作沿LOS的VER的Abel积分。而对于1.27 μ m波段, 在60 km以下的切线高度上自吸收效应较为强烈且不可忽略, 这使得测量光谱辐射强度变得更加困难。为精确模拟观测到的1.27 μ m波段O2(a1Δ g)气辉临边光谱辐射强度, 必须在考虑自吸收效应影响的情况下对VER路径积分进行计算。任意转动谱线J沿LOS在某一点的VER记为η J, 该转动谱线的光谱辐射强度作为波数v的函数, 则可以表示为

Be(v-vJ)=∫ztobsηE(J, s)D(v-vJ+Δv)×exp-∫ztobsn(s')σJD(v-vJ+Δv)ds'(4)

式(4)中, ηE(J, s)=εJ·nO2(a1Δg)(s), n为 O2(X3Σ)的分子数密度, σJ为给定转动谱线J的吸收截面, D(v-vJ+Δv)为s处的线形, Δv=vJV/c为大气风V沿LOS的位移。

图5(a)、(b)分别为30、 50、 70和90 km切线高度下有无自吸收效应的O2(a1Δ g)临边光谱辐射强度对比。可以看出, 当海拔高度位于70 km以上时, 光谱辐射强度并无明显差异, 而当海拔高度下降至50 km以下, 光谱辐射强度差异十分明显。该现象说明在海拔较低时自吸收效应对O2(a1Δ g)辐射光谱影响较为显著。其吸收量, 或者说有效光学厚度, 在很大程度上取决于沿LOS方向上的O2分子数密度。由于O2(a1Δ g)谱带两翼的转动谱线有效光学厚度较小, 受自吸收效应影响也较小, 因此可将两侧波长区域的发射线作为精确风温探测的目标谱线。

图5 不同切线高度下O2(a1Δ g)气辉临边辐射光谱强度
(a): 无自吸收效应; (b): 有自吸收效应Fig.5 Spectral intensity of O2(a1Δ g) airglow limbic radiation at different tangent heights
(a): Without self-absorption; (b): With self-absorption

1.2 大气散射光谱

临边观测模式下测得的光谱信号包括气辉辐射光谱和大气散射光谱两部分。由于太阳光在散射传输过程中会受到大气中气体分子吸收作用的影响, 因此大气散射光谱会携带分子的振-转光谱信息。大气散射过程会导致视线方向上部分气辉辐射出的光子被散射出相机视场外, 而部分位于相机视场外的太阳光也会被散射至相机感光面, 从而引起光稀释效应。在可见光区域, 气体分子的米氏散射和瑞利散射是引起光稀释效应的主要原因。在光稀释效应影响下, 尤其是在低切线高度处, 太阳光辐射背景对临边观测O2(a1Δ g)气辉光谱造成严重干扰。大气散射光谱是由吸收物质的光谱特性、 大气的气体浓度及气溶胶含量、 地表及云层的反射特性等诸多因素共同决定。

大气散射光谱辐射强度Bs可表示为瑞利散射和米氏散射沿LOS方向上点s处单位体积散射率的积分[19]

Bs(v)=∫ztobs[ηRs(v)+ηMs(v)]×exp-∫ztobsn(s')σJD(v-vJ+Δv)ds'(5)

式(5)中, η R和η M分别为点s处的单位体积散射率, 总的单位体积散射率可表示为 ηR, Ms(v)=ntFs(v)PR, M(ϕ )β R, M(v), 其中, PM, R(f)是散射角ϕ 处的瑞利散射或米氏散射相函数, β R, M(v)为频率v时瑞利散射或米氏散射的总截面, Fs是大气顶部的太阳光辐射强度, nt是大气总密度。

图6显示了切线高度35 km处1.27 μ m波段的临边大气散射光谱强度在不同地理气象条件下的变化情况。由于转动谱线在较低切线高度区域时受到多普勒展宽和压力展宽双重作用的影响, 导致其线型较宽, 其谱线呈现洛伦兹线形, 而在较高切线高度时, 其仅受到多普勒展宽影响, 其谱线呈现高斯线形。通过图5和图6对比可以看出, 大气散射光谱与O2(a1Δ g)气辉辐射光谱十分相似。然而受个别因素影响, 两者的光谱剖面略有不同。第一, 在高海拔地区, 多普勒展宽效应对散射光谱的影响占主导地位, 导致散射光谱线型较辐射光谱更宽。第二, 碰撞吸收发生在散射光谱中, 而在辐射光谱中并不存在, 这是由于碰撞吸收的影响与O2分子数密度成正比, 因此在高空区域该影响可忽略不计。第三, 当τ > 1时, 吸收过程是非线性的, 而气辉辐射过程保持线性。

图6 不同气溶胶、 反照率和云的情况下, 切线高度为35 km处的大气散射光谱强度Fig.6 Atmospheric scattering spectral intensity at the tangent height of 35 km for different aerosols, albedos and clouds

1.3 临边总辐射光谱

在临边观测模式下, 对于1.27 μ m波段的O2(a1Δ g)光谱带, 卫星遥感载荷可以同时观测到气辉的辐射光谱以及大气的散射光谱信号两部分, 两者的占比随海拔高度及太阳高度角的不同而发生急剧变化。由于在物理模型和数学算法中气辉辐射过程和大气散射过程都相对独立, 因此可以直接将这两个分量相加即可得到总的临边光谱辐射强度。如前所述, O2(a1Δ g)辐射波段的VER记为η E(s)(photons· cm-3· s-1), 每波数的大气体积散射率记为η S(s)(photons· cm-3· s-1· cm-1), 因此, 中心频率为vi的转动谱线的总光谱辐射亮度LTotal作为波数v的函数可以写成

LTotal(v)=∫-∞obs[ηE(s)fi(s)D(v-vJ+Δv, s)+ηRs(s)+ηRs(s)+ηGs(s)]×exp-∫sobsn(s')σJ(s')D(v-vJ+Δv, s')ds'ds(6)

式(6)中, fJ(s)和σ J(s)分别为转动谱线J沿LOS方向某一点s的相对辐射强度和吸收截面。 ηE(s)fi(s)D(v-vJ+Δv, s)为气辉发射分量, ηRs(s)、 ηMs(s)和 ηGs(s)为瑞利、 米氏和地面或云反射的大气散射分量。其中, O2(a1Δ g) VER可以用YM2011模型(由Yankovsky等开发的O2和O3光解产物电子振动动力学的完整模型[13, 14, 15, 17, 19, 20])计算得到。

O2(a1Δ g)光谱带在不同切线高度下的临边总光谱辐射强度如图7所示。可以看出, 气辉辐射光谱强度在50 km左右达到峰值, 且随海拔高度升高或降低缓慢下降。此外还可以看出, 大气散射光谱强度随海拔高度降低而剧烈增强。

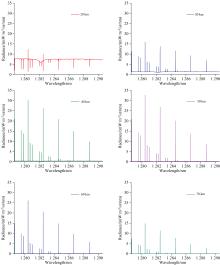图7 不同切线高度下临边光谱总辐射随高度的变化Fig.7 Variation of total limbic spectral radiation with height at different tangent heights

地面反照率、 气溶胶含量和云层厚度及类型对临边观测模式下O2(a1Δ g)光谱带的辐射传输特性具有显著影响。位于7 772.030 cm-1处的O19P18对光谱采样间隔的要求很低, 在光谱分离范围上具有很大优势, 可作为临边观测DASH仪器的最佳目标源[11]。图8为O19P18谱线在不同气溶胶、 反照率和云的影响条件下辐射强度的变化情况。其中横坐标表示波长, 纵坐标表示切线高度, 竖坐标表示光谱强度, 其强度值由右侧伪彩色表示。可以看出, 在只考虑瑞利散射的理想情况下, 20 km处的谱线两翼强度远远小于谱线中心处强度, 如图8(a)所示。加入大气中的气溶胶影响后, 该高度处辐射强度较上述情况增强了近6倍, 如图8(b)所示。如果再将地面反照率考虑在内(其值假设为0.5), 则该处辐射强度又将翻倍, 如图8(c)所示。最后考虑有云影响的情况, 该强度又将增加了150%, 如图8(d)所示。由于谱线中心的辐射强度在很大程度上受O2(a1Δ g)日辉的VER影响, 因此导致该处强度受地面反照率、 气溶胶和云的影响较小。气溶胶的存在会引起消光系数的变化, 进而可能导致低海拔区域的中心强度的变化。对于海拔高于20 km的空间区域, 气溶胶引起的米散射急剧降低, 其对光稀释效应的直接影响可以忽略。然而, 由于多次散射效应的存在, 低空区域气溶胶对太阳光的米散射, 以及云层及地表对太阳光的反照, 也会对高层大气的瑞利散射过程产生贡献, 从而影响星载仪器在高空区域的测风精度。

图8 O2(a1Δ g)气辉O19P18谱线在20~100 km切线高度辐射强度随气溶胶、 反照率和云变化
(a): 仅受瑞利散射影响; (b): 受瑞利散射和气溶胶影响; (c): 受瑞利散射、 气溶胶和地表反照率影响; (d): 受所有因素影响Fig.8 Variation of the radiative intensity of the O2(a1Δ g) airglow O19P18 spectral line at the 20~100 km tangent height with aerosol, albedo, and cloud
(a): Only Rayleigh scattering; (b): Rayleigh scattering and aerosols; (c): Rayleigh scattering, aerosols and albedo; (d): All effects

2 仪器正演仿真

大气运动导致O2(a1Δ g)气辉发生多普勒频移现象, 其频移量与风速成正比。气辉成像光谱仪在大光程差(optical path difference, OPD)条件下, 可以将风引起的微小的频移量转化为大的相位变化, 从而实现风速的高精度测量。DASH是近年提出的最新机理的气辉成像光谱仪, 由于不需要步进扫描, 且可以实现测量和定标的同步进行, 因而具有较高的探测效率和系统稳定性, 是高精细光谱卫星遥感, 尤其是星载测风仪器的首选方案。本文以DASH体制为例, 对正演结果进行仿真, 并在此基础上开展反演算法研究和误差分析研究。

2.1 仪器设计

DASH仪器的基本结构与迈克尔逊干涉仪类似, 其两臂的平面反射镜和平板玻璃分别由衍射光栅和楔形棱镜代替, 以同时获得大OPD和高对比度。由于光栅造成波面倾斜, 探测器阵列会记录下与波数有关的干涉条纹图案。通过对入射光信号进行傅里叶变换会产生一个空间条纹频率[21]。DASH阵列探测器记录的条纹干涉图与观测光谱之间的关系为[11]

H(x)=12∫0∞L(v)T(v)[1+cos{2π[4(ν-νL)tanθLx+2v·Δd]}]dv(7)

式(7)中, L(v)为大气光谱亮度, T(v)为滤光片的透射函数, νL=1/(2gsinθL)为利特罗波数, θL为光栅的利特罗角, 1/g为光栅的槽密度, x为OPD在探测器阵列上对应的位置, 2Δ d为干涉仪其中一个光路的额外OPD偏移量。

2.2 正演仿真

临边观测DASH仪器探测得到的原始干涉图像包含O2(a1Δ g)日辉辐射信号和光稀释效应影响下的太阳光散射背景信号。气辉辐射信号产生了理想的干涉条纹, 太阳散射光谱产生了恒定的背景, 叠加在干涉条纹上。DASH仪器专用于测量大气风场, 同时监测校准信号以监测仪器的偏移, 其干涉图的亮度和条纹对比度包含了发射线密度和线型信息。单条发射线的相移δ φ 可表示为

δφ=4πΔdσ(s/c)=2πk(s/c)(8)

式(8)中, σ 为发射线的非多普勒位移波数, s为多普勒速度, c为光速。

DASH仪器测得的干涉图样的处理过程如图9所示。在实际观测中, 特别是在低切线高度区域, 干涉图的每一行都包含了O2(a1Δ g)日辉辐射信号和太阳散射背景信号。通过简单地傅里叶变换, 可将干涉图中非调制项去除[22], 得到太阳光散射背景。用初始的干涉图减去太阳光散射背景, 即可恢复纯O2(a1Δ g)气辉辐射的信号图像。需要指出的是, 光稀释效应产生的无效信号会增加仪器的散粒噪声, 在扣除无效信号的过程中, 噪声不仅无法扣除, 反而会与气辉信号产生的散粒噪声累加, 共同对星载仪器的测风精测产生影响。

图9 DASH仪器干涉图样的处理过程Fig.9 Processing of interferometric patterns for the DASH instrument

干涉图中每一行图像均包含来自不同层的大气信息贡献, 这些层具有不同的风速、 温度和体发射率等大气参数。为获得仅包含目标高度层信息的干涉图, 还需使用“ 剥洋葱” 算法对O2(a1Δ g)气辉辐射信号进行处理。图9中使用的大气风场剖面取自美国海军研究实验室更新的水平风模型[23]。在干涉图像的模拟过程中, 考虑了三种主要噪声源, 包括散粒噪声、 读出噪声和探测器暗噪声。其中, 散粒噪声由O2(a1Δ g)气辉信号和大气散射信号共同贡献, 读出噪声和仪器暗噪声参数取自Wu等的工作[11]。

3 反演算法
3.1 “ 剥洋葱” 算法

DASH仪器采用临边观测模式获取大气信息, 以测得高分辨率垂直风廓线。其干涉图信号包含每一行来自相应LOS的临边观测高度的气辉辐射, 由于观测几何影响, 该行信号包含有目标层及其以上空间高度大气层的贡献。为消除其他层贡献造成的影响, 利用“ 剥洋葱” 算法对所采集的信号进行处理。

“ 剥洋葱” 算法的数学处理过程是, 从最上层视线开始求解, 上一层的求解结果作为下一层的输入, 依次向下求解。由于顶层高度没有其他高度的贡献, 可以直接从顶层临边测量中获得目标层信号强度。然后, 从第二层测量值中去除顶层高度的贡献, 即可得到第二层目标段的信号强度。依此类推, 即可得到各临边高度目标层的信号强度信息。其表达式可写为[8]

I0(x)ejΔφ0=1ω00H0(x)(9)

Im(x)ejΔφm=1ωmmHm(x)-∑n=0m-1In(x)ejΔφncosαmnωmn

∀m∈[1, M-1]

式(9)中, M为分离的大气层数, Im为FPA第m行干涉图, Δ φ n为第n层水平风引起的相移, α mn为水平面与第m个LOS与第n层交点处的夹角, ω mm为高度n处第m个LOS的权值。反演从m=0开始, 依次迭代进行。

值得注意的是, 由于存在自吸收效应, DASH仪器不能直接将O2(a1Δ g)气辉作为目标源, 在求解LOS积分时, 必须考虑O2(X3Σ )的自吸收过程。

3.2 误差分析

DASH测风的误差主要由仪器的灵敏度与光学分辨率, 以及散粒噪声、 读出噪声和探测器暗噪声等噪声来源决定, 且受气辉辐射强度及大气光稀释效应影响。基于最优化估计的概念对大气风场反演的过程各因素的具体影响进行量化分析, 利用误差传递原理, 可对有效评估大气光稀释效应对测风精度的影响。Englert等详细描述了从测量干涉图到反演相位的噪声传递过程[24]。根据测风误差与有效信噪比的函数关系可知, 在> 50 km高度范围内的O2(a1Δ g)日辉辐射过程中, 其有效信噪比依赖于当地太阳时和太阳活动; 而对于< 50 km的高度范围, 其有效信噪比由单一发射线大气信号和组合信号之比决定。

对临边观测DASH仪器所探测信号进行仿真可以得到信号图像的信噪比, 从而能够实现对测风精度误差的定量分析。不同气象地理条件下仿真得到的干涉图样信噪比如图10所示, 其纵轴包含高度信息, 横轴表示OPD, 信噪比对应于OPD的强度变化用图像右侧的伪彩色表示。可以看出, 信噪比在不同气溶胶、 地表反照率和云量条件影响下存在显著差异, 太阳散射光谱的干扰会导致干涉图条纹对比度降低并且会使测量噪声增强。总体而言, 当仅存在瑞利散射的理想情况时, 信噪比最高, 当散射过程逐渐复杂时, 信噪比相应降低。

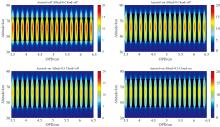图10 不同气溶胶、 地表反照率和云量条件下DASH干涉图像的信噪比Fig.10 Signal-to-noise ratio of DASH interferometric images under different aerosol, surface albedo and cloudiness conditions

为更清晰展示光稀释效应对DASH测风精度的影响, 不同气象地理条件下信噪比随临边观测高度的变化情况在图11(a)中给出。可以看出, 信噪比在60 km附近达到峰值, 这是由于高海拔处O2(a1Δ g)气辉的VER降低, 而低海拔处气辉辐射光谱受大气散射污染严重。对于临边观测模式, 除信噪比外, 测风精度也会受目标层气辉强度的相对权重以及干涉图对比度的影响。综合考虑上述因素计算得到的不同气象地理条件下测风误差随临边高度的变化情况如图11(b)所示。可以看出, 在45~80 km范围内, 多普勒风的随机误差在2~3 m· s-1范围内。在较高切线高度处, 由于信噪比急剧降低, 导致该范围内风速误差呈指数型增长。在45 km以下高度范围内, 干涉图像受大气光稀释效应的影响程度增加, 同样导致了测风精度的降低。对于一个卫星载荷, 若其对风速测量误差的要求优于10 m· s-1, 在纯瑞利散射的理想情况下, 探测高度范围下限可达35 km, 当同时考虑大气气溶胶影响的情况下, 其探测高度下限升高至38 km, 在多云天气时, 该下限进一步上升至40 km。这是由于散粒噪声在很大程度上依赖于太阳散射背景, 而地表反照率、 气溶胶和云量的变化必然会导致有效信噪比的变化, 从而影响测风精度。

图11 不同地表反照率、 气溶胶和云量影响下30~90 km范围内信噪比和测风精度的变化
(a): 信噪比; (b): 风速误差Fig.11 Signal-to-noise ratio and wind measurement precision as a function of altitude in the 30~90 km range under the influence of different surface albedos, aerosols and cloud
(a): Signal-to-noise ratio; (b): Wind speed error

4 总结

针对星载DASH仪器以O2(a1Δ g)日辉为目标源进行临近空间大气风场探测, 全面深入地研究并讨论了光稀释效应对测风精度的影响。在1.27 μ m的O2近红外大气波段可以同时观测到辐射谱和吸收谱, 地表反照率、 气溶胶含量以及云的存在与否对于O2(a1Δ g)气辉临边辐射传输特性具有显著影响。基于大气气辉辐射传输理论和临边观测DASH仪器概念, 本文对光稀释效应影响下的卫星遥感干涉图像进行了正演仿真, 详细描述了剥离太阳散射背景并生成纯净单一气辉光谱信号图像的具体过程, 然后阐述了在考虑自吸收效应的情况下, 使用“ 剥洋葱” 算法反演得到仅包含目标层高度信号的干涉图像的具体方案。由于太阳散射背景的存在降低了干涉图像的对比度, 同时增加了测量噪声, 对临边观测权重和有效信噪比产生了不利影响。针对该问题, 本文进行了详细的误差分析, 研究结果表明, 在45~80 km切线高度范围内, 大气散射对测风精度影响较小, 误差约为2~3 m· s-1; 而在45 km以下, 测风精度受光稀释效应的影响随海拔高度的降低而急剧增大, 且受地表反照率、 气溶胶和云量等因素的影响显著升高。对于10 m· s-1的可接受误差水平, 仅考虑瑞利散射影响时, 探测高度下限约为35 km, 在多云天气下增加至40 km。

在未来的工作中, 我们将重点考虑如何优化设计仪器参数(如滤光片透射带宽及干涉仪光谱分辨率等)及反演算法, 以尽量减少光稀释效应对星载被动风场探测精度的影响, 并拓展星载气辉成像仪的探测高度下限。

参考文献
[1] Wang W Q. Near-Space Vehicles in High-Resolution Wide-Swath Remote Sensing, Springer Science & Business Media, 2011. doi: 10.1007/978-3-642-22188-0. [本文引用:1]
[2] FENG Yu-tao, LI Juan, ZHAO Zeng-liang, et al(冯玉涛, 李娟, 赵增亮, 等). Aerospace Shanghai(上海航天), 2017, (3): 14. [本文引用:1]
[3] Baumgarten G. Atmospheric Measurement Techniques, 2010, 3(6): 1509. [本文引用:1]
[4] LI Jian-yu, SUN Feng-ying, LI Xue-bin, et al(李建玉, 孙凤萤, 李学彬, 等). Chinese Journal of Scientific: Instrument(仪器仪表学报), 2019, 40(7): 121. [本文引用:1]
[5] DONG Bao-ju, ZHANG Ye, XU An-lun, et al(董保举, 张晔, 徐安伦, 等). Journal of Yunnan University (Natural Sciences Edition)[云南大学学报(自然科学版)], 2011, (S1): 18. [本文引用:1]
[6] FAN Zhi-qiang, SHENG Zheng, WAN Li, et al(范志强, 盛峥, 万黎, 等). Acta Physica Sinica(物理学报), 2013, 62(19): 199601. [本文引用:1]
[7] Šavli M, de Kloe J, Marseille G J, et al. Quarterly Journal of the Royal Meteorological Society, 2019, 145(725): 3499. [本文引用:1]
[8] Harding B J, Makela J J, Englert C R, et al. Space Science Reviews, 2017, 212: 585. [本文引用:2]
[9] Ward W E, Gault W A, Shepherd G G, et al. Proceedings of SPIE—The International Society for Optical Engineering, 2001, 4540. [本文引用:1]
[10] He Weiwei, Wu Kuijun, Feng Yutao, et al. Remote Sensing, 2019, 11(8): 914. [本文引用:1]
[11] Wu Kuijun, Fu Di, Feng Yutao, et al. Optics Express, 2018, 26(13): 16984. [本文引用:5]
[12] Harding B J, Makela J J, Qin J, et al. Journal of Geophysical Research: Space Physics, 2017, 122: 7654. [本文引用:1]
[13] Yankovsky V A, Manuilova R, Babaev A, et al. International Journal of Remote Sensing, 2011, 32(11): 3065. [本文引用:2]
[14] Yankovsky V A, Martyshenko K V, Manuilova R O, et al. Journal of Molecular Spectroscopy, 2016, 327: 209. [本文引用:2]
[15] Martyshenko K V, Yankovsky V A. Geomagnetism and Aeronomy, 2017, 57: 229. [本文引用:2]
[16] Gordon I E, Rothman L S, Hargreaves R J, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2022, 277: 107949. [本文引用:1]
[17] Emmert J T, Drob D P, Picone J M, et al. Earth and Space Science, 2021, 8(3): e2020EA001321. [本文引用:2]
[18] Berk A, Conforti P, Kennett R, et al. 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2014. [本文引用:1]
[19] Yee J H, Demajistre R, Morgan F. Canadian Journal of Physics, 2012, 90(8): 769. [本文引用:2]
[20] Yankovsky V A, Babaev A S. Atmospheric and Oceanic Optics, 2011, 24: 6. [本文引用:1]
[21] Englert C R, Harland er J M, Emmert J T, et al. Optics Express, 2010, 18(26): 27416. [本文引用:1]
[22] Wu Y J J, Harding B J, Triplett C C, et al. Earth and Space Science, 2020, 7(10): e2020EA001164. [本文引用:1]
[23] Drob D P, Emmert J T, Meriwether J W, et al. Earth and Space Science, 2015, 2(7): 301. [本文引用:1]
[24] Englert C R, Babcock D D, Harland er J M. Applied Optics, 2007, 46(29): 7297. [本文引用:1]