作者简介: 盖巧娜,女, 1997年生,北京信息科技大学仪器科学与光电工程学院硕士研究生 e-mail: 1042257578@qq.com
中阶梯光栅光谱仪兼具光谱范围宽和光谱分辨率高的优势, 为将因中阶梯光栅衍射级次高而导致混叠的光谱分开, 中阶梯光栅光谱仪的色散系统使用了两个分别在相互垂直的方向进行交叉色散的元件, 并最终在探测器上形成二维光谱图像。 为了获取光谱仪所检测物质的直观光谱信息, 需要通过谱图还原算法将二维光谱图像转换成光强与波长对应的一维谱图, 谱图还原算法的优劣直接决定了中阶梯光栅光谱仪的精度和效率。 结合已有的谱图还原算法, 提出了一种改进的分段多项式拟合的二维谱图还原算法。 该算法所基于的中阶梯光栅光谱仪采用透射式棱镜, 与传统的光线追迹获取拟合数据点的方法不同, 通过中阶梯光栅和棱镜的色散规律获取波长所对应的像元坐标数据, 之后将探测器像面在横轴上按像元坐标划分成多个区域; 由于 X坐标与衍射级次 m具有一定的相关性, 因此算法的原理是通过建立 X坐标与 m的拟合关系式, 即可由光线落在探测器像面的 X坐标得到光线所属衍射级次, 并结合像面的Y坐标与波长的关系式最终得到坐标与波长的关系式; 分别对各个区域进行多项式拟合, 得到每个区域的波长与像元坐标的关系式, 实现整个区域谱图还原模型的建立。 实验表明: 所建立的谱图还原模型的计算误差为0.000 1 nm。 综上, 该算法运算简单、 能够快速实现谱图还原, 并且提高了谱图还原的准确率。
The middle Echelle grating spectrometer has the advantages of wide spectral range and high Spectral resolution. To separate the spectra that are aliased due to the high diffraction order of the middle Echelle grating, the dispersion system of the middle Echelle grating spectrometer uses two elements that conduct cross dispersion in mutually perpendicular directions, and finally forms a two-dimensional spectral image on the detector. To obtain the intuitive spectral information of the substances detected by the spectrometer, it is necessary to convert the two-dimensional spectral image into the one-dimensional spectral image corresponding to the light intensity and wavelength through the spectral image reduction algorithm. The quality of the spectral image reduction algorithm directly determines the material analysis accuracy and efficiency of the middle Echelle grating spectrometer. An improved piecewise polynomial fitting two-dimensional spectrogram restoration algorithm is proposed based on existing spectrogram restoration algorithms. The middle Echelle grating spectrometer based on the algorithm in this paper uses a transmission prism, which is different from the traditional method of ray tracing to obtain fitting data points. The pixel coordinate data corresponding to the wavelength is obtained through the dispersion law of the middle Echelle grating and prism. Then the detector image surface is divided into multiple areas according to pixel coordinates on the horizontal axis; Due to the certain correlation between the X coordinate and the diffraction level m, the principle of the algorithm is to establish a fitting relationship between the X coordinate and m, which can be used to obtain the diffraction level of the light ray from the X coordinate of the detector's image plane. By combining the relationship between the Y coordinate of the image plane and the wavelength, the relationship between the coordinate and the wavelength can be obtained. Perform polynomial fitting on each region to obtain the relationship between each region's wavelength and pixel coordinates and establish a model for restoring the entire region spectrum. Experimental verification shows that the calculation error of the established spectrogram reduction model is 0.000 1 nm. In summary, the algorithm designed in the paper has simple operations, can quickly achieve spectral restoration, and improves the accuracy of spectral restoration.
中阶梯光栅光谱仪同时兼具分辨率高、 光谱检测范围宽、 体积小、 光谱采集速度快等优势, 得到越来越多的重视, 逐渐发展为光谱检测领域的热门与重点。 由于中阶梯光栅制造工艺和探测器发展水平的约束限制, 加上光谱重叠等问题, 早期中阶梯光栅光谱仪的发展极为缓慢[1]。 直至二十世纪九十年代, 在解决了光谱重叠问题后, 光栅和探测器也取得了较大进步, 中阶梯光栅光谱仪才重新受到关注, 目前在天文探测、 化学材料、 土壤检测、 生物医学等领域都有广阔的应用前景[2, 3, 4, 5]。
中阶梯光栅与普通平面光栅不同, 它的刻线密度较低, 通常为30~300 gr· mm-1 [6]。 由于中阶梯光栅通常工作在较高的衍射级次, 所以它的自由光谱区窄, 存在严重的光谱重叠问题。 为了将重叠的光谱分开, 实现级次分离, 需要在中阶梯光栅后增加一个二次色散元件, 色散方向垂直于中阶梯光栅的色散方向, 实现交叉色散, 这就使得光谱仪在探测器像面形成的光谱为二维光谱[6]。 二维图像无法直接用于光谱识别与分析, 为了获得检测对象的光谱信息, 需要通过谱图还原方法对二维光谱图像进行处理转换, 得到波长与像面坐标一一对应的关系[7, 8]。 目前光线追迹法是国外采用较多的谱图还原方法, 利用光学设计软件搭建对应的光路仿真模型, 任意波长的光线都可以通过追迹确定它在探测器像面上的具体位置坐标, 从而得到波长与坐标的关系, 实现谱图还原[9]。 但是这种方法过程繁琐, 当检测波段范围宽, 光谱数据量大时需要大量光线追迹, 花费时间较长。 中阶梯光栅光谱仪的色散棱镜可分为反射式和透射式两种。 国内中阶梯光栅光谱仪研究发展起步虽较晚, 但近年来也取得了一些成果, 如陈少杰[10]、 张锐[11]等分别针对上述两种光谱仪设计了谱图还原算法, 根据所研究光谱仪的色散元件以及系统结构特点, 通过角度近似、 公式推导等方法建立色散公式, 并进行大量数据计算得到波长与坐标的对应关系矩阵; 该方法计算量较大, 且当坐标数据量较大时, 通过矩阵查询对应波长所耗费的时间较长。 朱继伟[12]采用光线追迹拟合多项式, 虽然通过级次间拟合可将光线追迹的数量减少, 但是参与拟合的数据点少, 容易产生误差; 且棱镜具有色散不均匀性, 整个像面采用一个拟合公式表达X坐标与波长的关系, 可能会存在欠拟合的情况。
本研究的中阶梯光栅光谱仪分光元件由中阶梯光栅和透射式色散棱镜组成。 将探测器像面按X坐标划分成多个区域, 首先根据棱镜的色散规律, 求得波长对应的X坐标, 分别对每个区域将求得的X坐标与波长对应的衍射级次m进行多项式拟合, 得到m=f(x)的多项式; 其次根据光栅色散规律, 结合Y坐标与波长的关系最终计算得到波长与像元坐标的对应公式。 该方法增加了拟合的数据点, 提高了拟合公式的可靠性和波长还原的准确性, 并且减少了通过建立波长与坐标的矩阵并查表进行谱图还原所需的运算时间, 提高了光谱还原的运算效率, 算法灵活性较高。
与传统的C-T型光谱仪采用的平面光栅不同, 中阶梯光栅并不借助于增大光栅刻线密度的方法来提高光谱仪的分辨率, 而是凭借闪耀角大、 衍射级次高等特征使对应的中阶梯光栅光谱仪有着较高的分辨率[13]。 为了解决中阶梯光栅因衍射级次高而产生的自由光谱区窄、 光谱重叠在一起的问题, 引入棱镜作为二次色散元件进行交叉色散[14], 交叉色散形成的二维谱图对后期的光谱分析造成了一定的困难。 所以建立快速高效、 准确率高的谱图还原模型是十分必要的, 直接决定了中阶梯光栅光谱仪对物质的识别与分析效率。
透射式棱镜与反射式棱镜相比少了反射面, 能量损耗少, 有利于探测器对弱信号的接收。 谱图还原算法所基于的中阶梯光栅光谱仪结构为透射式棱镜的C-T型光路结构。 如图1所示, 入射光线通过狭缝后, 经过准直镜准直, 光线平行入射至中阶梯光栅。 为了便于后续元件对光线的接收, 同时又能得到中阶梯光栅最大的衍射效率, 中阶梯光栅以一定的偏置角放置, 使光线满足准李特洛条件入射到中阶梯光栅上。 光线经中阶梯光栅在纵向色散后, 入射到透射式棱镜进行横向色散, 光线经交叉色散并最终经聚焦镜汇聚落在像面被探测器接收。 中阶梯光栅光谱仪的探测器采用德国Allied Vision公司的曼塔G-235系列, 像素为1 936× 1 216, 像元尺寸为5.86 μ m。
所研究的中阶梯光栅光谱仪的技术参数如表1所示。
| 表1 中阶梯光栅光谱仪技术参数 Table 1 Technical parameters of echelle grating spectrometer |
中阶梯光栅作为光谱仪的主色散元件, 为了便于光线进入下一色散元件, 利于探测器光谱接收, 通常以一定偏置角放置[15], 它的光栅方程为
式(1)和式(2)中, m为光栅衍射级次, λ 为入射光线波长, d为光栅常数, γ 为光栅偏置角, i为光栅的光线入射角, β 为衍射角。
使中心波长光线满足李特洛条件入射, 即
中心波长计算公式为
其中β 0为每一衍射级次中心波长光线的衍射角, θ 为中阶梯光栅的闪耀角。 λ cen为各级次中心波长, 由中心波长的计算公式可得, 各衍射级次的中心波长落在探测器Y轴像元坐标点的位置是相同的。
本研究的中阶梯光栅光谱仪采用透射式棱镜, 它的光线传输关系分析如式(5)
式(5)中, i1为棱镜的光线入射角, i'1为光线经棱镜第一次折射后的折射角, n(λ )为不同波长光线对应的折射率。 则
式(6)和式(7)中, A为棱镜顶角, i2为光线经棱镜第二次折射时的入射角, i'2为光线第二次折射时的出射角。
由式(5)— 式(7)可得, 已知棱镜的顶角和光线入射角, 不同波长的光线入射棱镜后, 棱镜出射角与棱镜折射率的关系为
其中棱镜折射率根据波长变化的经验公式通常由Sellmeier公式描述[13], 其公式可表示为式(9)
B、 C作为Sellmeier系数, 不同的玻璃材料B、 C值不同, 可通过公开的资料库查到具体材料的B、 C值。 光谱仪采用熔融石英作为棱镜材料, 表2为熔融石英的Sellmeier系数。
| 表2 熔融石英Sellmeier系数 Table 2 Sellmeier coefficient of fused silica |
对于同一棱镜材料, 不同波长的光线入射棱镜后对应的折射率不同, 因而棱镜可以将不同波长的光分开。 光线进入中阶梯光栅光谱仪, 经中阶梯光栅色散后, 由于级次混叠导致的不同波长的光线落在探测器Y轴同一点, 棱镜的作用就是将Y轴同一位置混叠的波长在X轴方向分开。 光线落在探测器像面上的X坐标为
式(10)中, f为光谱仪聚焦镜焦距, Δ i为光线由棱镜出射后, 不同波长与选定的参考波长之间的出射角的差值, 可由式(8)求得, 参考波长为落在像面Y轴同一点的所有混叠光线中的最大波长值, c为探测器像面的单个像元尺寸。
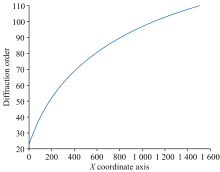
棱镜色散分光后光线落在X轴的位置与光线所对应的衍射级次呈相关性, 如图2所示。 因而可以通过建立像元X坐标与衍射级次m的拟合关系式, 即可由光线在探测器像面成像的X坐标得到光线所属衍射级次, 用于后续波长计算。
但是棱镜色散具有不均匀性, 短波波段棱镜折射率较大, 长波波段棱镜折射率较小。 因此导致像面上长波波段所对应的光谱衍射级次之间距离间隔小、 短波波段对应的级次距离间隔大且斜率较大[12]。 若只采用一个公式对整个像面的X坐标与衍射级次进行拟合, 会导致拟合误差较大, 因此采取分段拟合方式, 将像面在X轴方向上按坐标划分为几个区域, 对每个区域分别建立拟合公式, 拟合原理如下所述:
(1)根据所采用的探测器的像元数目, 将探测器像面划分为n段。 考虑到棱镜色散在长波波段变化小, 因此将前两百个像元坐标每五十为一段, 其余以一百个像元为一个区域段。 由于所研究的光谱仪采用的探测器横轴像元数目为1 216个, 所以将其划分为14个区域, 每一个区域像元个数为1 936× 50或1 936× 100。
(2)利用式(4)的中心波长计算公式求得每个衍射级次的中心波长。 衍射级次范围可通过式(11)和式(12)求得
式(11)和式(12)中mmax、 mmin分别为所研究光谱仪衍射级次的最大、 最小值, λ min、 λ max分别为光谱仪检测范围的波长最大、 最小值。
(3)计算出各衍射级次的中心波长所对应的X坐标。 将各衍射级次的中心波长值代入式(10)求得对应的X坐标。
(4)在每一区域内, 建立所求X坐标与衍射级次m的拟合关系式
(5)通过光线落在像面的X坐标可求得光线所属的衍射级次m。
(6)同一衍射级次, 光线衍射角随波长的不同而变化, 其计算公式为
不同波长光线落在探测器像面不同Y坐标上, 则光线在光栅色散方向上衍射角的变化为
式(15), Δ β 为光栅色散方向各个波长的衍射角与中心波长衍射角相比的改变量。 Y表示探测器的像元Y坐标, N表示探测器纵轴像元数目。
将式(14)、 式(15)代入式(2)中, 则波长计算公式为
(7)获取光线落在探测器上的位置坐标后, 利用m=f(x)的关系式可求得探测器所检测到的信号光斑所属的衍射级次, 结合Y坐标可计算得到光斑的波长。 最终通过多项式拟合求得波长与坐标的关系式为
根据上述分析, 整个二维像面的波长分布图如图3所示。
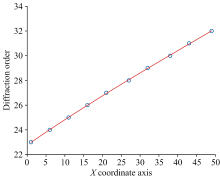
探测器像面可用图3的示意图表示, 纵轴方向使坐标原点处于像面中心, 恰好为各衍射级次中心波长所处位置, 横轴方向使原点与边界重合。 光谱衍射级次为23~100级次, X坐标覆盖1~1 100像元, Y坐标范围为-968~968。 按照X坐标分区域后, 分别建立X与m的拟合关系式, 其中0~50区域的拟合结果如图4所示。
根据上述步骤, 可实现二维谱图还原, 建立谱图还原模型。 取一系列坐标, 通过多项式拟合计算得到波长, 与理论波长值对比验证所设计谱图还原算法的精度, 验证结果如表3所示。
| 表3 拟合与理论波长对比 Table 3 Comparison between fitting and theoretical wavelengths |
由于采用中心波长的X坐标进行多项式拟合, 因此结果验证时, 采用非拟合数据进行验证, 即采用除各衍射级次中心波长以外的波长, 以及对应的X、 Y坐标进行验证。 实验抽取15组数据, 最终验证拟合的误差为0.000 1 nm, 满足光谱仪的精度要求。 因此本谱图还原算法能够准确且高效地进行二维谱图还原, 得到一维光谱信息。
算法的实际处理过程首先是利用中阶梯光栅光谱仪拍摄二维光谱图像, 如图5所示对二维图像预处理, 得到二值化图像。
利用质心提取算法, 对图5的光斑进行质心提取, 将得到的光斑质心在图上标出, 如图6所示。 质心坐标即为光线被探测器接收所对应的坐标, 将光斑质心坐标代入上述谱图还原算法, 即可由坐标计算得到对应的波长, 完成二维谱图还原。
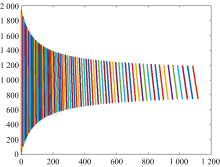
如图7所示, 上述谱图还原算法可建立谱图还原模型。
在自由光谱区内, 谱图还原模型的Y轴表示光栅色散方向, X轴表示棱镜的色散方向。 Y轴方向上每条线都代表了光谱仪的一个衍射级次, 其中光线波长越短, 所属的衍射级次越高, 从左至右波长逐渐变短, 自由光谱区也就越短。 同时由于棱镜的色散不均匀性, 短波波段折射率高, 长波波段折射率低, 因此谱图还原模型呈现了左密右疏的情况。 谱图还原的过程就是将如图5一样的二维光谱图像利用谱图还原模型实现坐标与波长一一对应, 将二维光谱图转换成一维光谱的过程。
对中阶梯光栅光谱仪现有的谱图还原算法进行了改进, 结合公式法得到初始拟合数据, 后对多项式拟合的谱图还原算法进行了改进, 建立了分段式多项式拟合的谱图还原模型。 根据探测器像面X轴的像元数目, 把像面划分成多个区域, 且考虑到棱镜色散不均匀性采用非均分划分区域。 针对每一个像面区域, 将通过中阶梯光栅光谱色散元件的元件参数以及色散规律得到的各衍射级次的中心波长X坐标与光谱衍射级次m进行拟合, 得到X坐标与m的多项式拟合关系式m=f(X), 可通过X坐标计算得该光斑所属衍射级次m, 将关系式代入波长与Y坐标和m的公式中, 由此得到谱图还原模型。 取15组坐标数据, 将多项式拟合计算得到的结果与理论波长值进行对比, 验证了所建立的谱图还原模型误差为0.000 1 nm。 通过对谱图还原算法的改进, 该方法无需利用光学设计软件进行复杂的仿真, 不需要进行光线追迹, 减少了光线追迹的繁琐步骤; 并且增加了参与拟合数据点的数量, 更加方便实用, 提高了拟合的准确性。 与传统的公式法相比, 计算量少, 无需查找模型矩阵直接通过坐标计算效率更高。 该方法能够快速实现谱图还原, 精度高, 拟合思路适用于不同种类的光谱仪, 具有普适性。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|