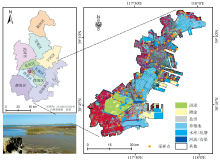
天津滨海新区位于华北平原北部, 环渤海地区的中心地带(38° 40'— 39° 00'N, 117° 20'— 118° 00'E), 气候属于暖温带半湿润大陆季风型气候, 并具有海洋性气候特点, 年均气温12 ℃, 年降水量500~800 mm。 滨海新区拥有丰富的湿地资源(图1), 包括北大港湿地自然保护区、 天津市海洋牧场示范区、 蓟运河营城段芦苇湿地、 天然淤泥滩涂湿地以及黄港一库、 黄港二库、 北塘水库、 水产养殖场、 盐田等湿地^[17]。 土壤母质以河流冲积物为主, 区内湿地土壤类型主要为潮土、 滨海盐土、 草甸盐土和盐化湿润土。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区及采样点分布示意图Fig.1 Distribution diagram of the study area and sampling points

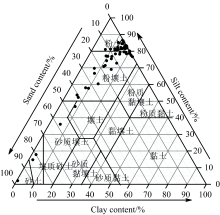
于2021年10月开展湿地土壤采集, 综合考虑湿地分布与交通可达性等因素布设采样点, 样点间直线距离约为1 km, 通过5点混合法收集0~20 cm的表层土壤样品, 装入密封袋保存, 记录采样点环境状况并使用GPS获取坐标信息, 共计得到57个湿地土壤有效样本(图1), 每个样本分成两份, 分别用于土壤光谱测量和土壤粒径分析。 土壤样品经室内自然风干、 剔除杂质和研磨后过2 mm细孔筛, 采用H₂O₂-HCl-(NaPO₃)₆法对土壤样本预处理。 土壤质地采用NKT6100-D激光粒度仪测定, 其原理为激光衍射/散射测量技术, 根据衍射散射光强度分布和接受散射光强度信号计算出颗粒粒径和所占总数的体积百分含量^[18], 测量粒径范围为0.012~2 000 μ m, 得到土壤粒径体积分数, 根据美国土壤粒径分级标准分级: 黏粒(< 2 μ m)、 粉粒(2~50 μ m)、 砂粒(50~2 000 μ m)。 测试发现研究区湿地表层土壤质地类别主要分布在粉土、 粉壤土、 壤土、 砂质壤土、 壤质砂土和砂土的区域范围内, 其中以粉壤土和粉土为主(图2)。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 土壤质地三角图Fig.2 Soil texture triangle plots

土壤光谱采用美国ASD公司生产的便携式地物光谱仪(FieldSpec 4)测定, 光谱范围为350~2 500 nm。 在室内避光环境中进行, 将适量待测土壤样品放入器皿内并刮平表面, 每个土壤样品测量前进行白板校正, 重复采集10条光谱曲线, 取平均值作为土壤样品的原始光谱反射率。 因土壤光谱反射率中350~399和2 401~2 500 nm噪声较大、 信噪比较低, 仅选取400~2 400 nm范围内的光谱反射率数据进行分析建模, 经1 nm间隔的重采样后得到2 001个波段。

为减少细节噪声、 基线漂移等干扰, 提高土壤粒径含量对光谱的敏感程度, 采用S-G平滑(阶数为2)对原始光谱平滑去噪(reflectivity, R), 进行一阶微分(first derivative, FD)、 倒数(reciprocal transformation, RT)、 平方根(square root, SR)、 倒数之对数(logarithm of reciprocal, LR)、 倒数一阶微分(RTFD)、 平方根一阶微分(SRFD)和倒数之对数一阶微分(LRFD)八种形式光谱变换, 分析不同光谱变换对三种粒径含量估测的影响。 将三种粒径含量与不同光谱变换波段反射率之间进行Pearson相关系数分析。

本文获取的可见光-近红外高光谱数据具有波段连续性强, 光谱信息冗杂, 且各波段之间存在多重共线性, 通过CARS算法进行特征优选, 以减弱波段之间的多重共线性和降低数据冗余。 CARS算法是基于蒙特卡罗(monte carlo, MC)采样法和PLSR模型的一种特征波长选择方法^[10]。 模拟生物进化论中的“ 适者生存” 法则, 通过使用指数衰减函数(exponentially decreasing function, EDF)和自适应加权采样来计算回归系数绝对值的权重, 去除掉权重较小的波长变量, 保留权重较大且共线性小的波长变量组合成新的变量子集, 分别建立PLSR模型, 选取交叉验证均方根误差(root mean square error of cross validation, RMSECV)最小的PLSR模型所对应的波段作为最终的特征波段。

采用偏最小二乘、 支持向量机与随机森林三种机器学习算法进行不同粒径含量估测, 通过R语言pls包、 e1071包、 randomForest包实现。

偏最小二乘回归(PLSR)融合了主成分分析、 典型相关性分析和多元线性分析方法于一体, 提取和筛选对因变量解释性强的主成分变量, 能够简化数据结构和分析变量之间相关性, 在处理自变量之间高度相关性问题和样本数量小于变量的情况, 具有良好的鲁棒性^[9]。

随机森林回归(RFR)模型采取随机采样方式建立大量回归树, 将不同决策树的加权平均值作为最终的预测结果。 RFR模型能够识别自变量与因变量之间复杂的非线性关系, 对数据要求低, 能够处理高维数据, 具有很好的抗噪声能力, 不易出现过拟合现象^[16]。 整体模型的结果具有较高的精确度和泛化性能, 与参数回归方法相比较, 实现比较简单, 也不需要考虑多变量的共线问题。 通过调整决策树的数量(ntree)和分裂特征数量(mtry)来获取最优模型。

支持向量机回归(SVR)是一种小样本数据的监督学习算法, 通过结构风险最小化原则, 避免了对数据量的高度依赖^[15]。 SVR将非线性的数据映射到高维数据特征空间中, 使自变量与因变量在高维空间中具有良好的线性回归特征, 进而实现原始空间中的非线性回归^[16]。 选取径向基函数为核函数, 根据均方根误差最小原则优化惩罚系数(C)和核参量(gamma)构建最优SVR模型。

采用分层随机抽样方法对57个土壤样本进行训练集与测试集的划分, 训练集样本数量约占总体样本的72%, 共41个样本, 剩余16个样本为测试集样本, 保证训练集模型建立和测试集验证的合理性与可靠性, 所有训练模型选用留一法交叉验证(leave-one-out cross-validation, LOOCV)。 模型精度评价指标选用决定系数(R²)、 均方根误差(RMSE)和归一化均方根误差(normalized root mean squared error, nRMSE)。 R²取值范围在0~1之间, R²越接近于1, 说明该模型的稳定性越好、 拟合程度越高。 RMSE和nRMSE用来检验模型的估测能力, 数值越小, 模型估测精度越高。 nRMSE的计算公式如式(1)

nRMSE=RMSE(ymax-ymin)(1)

式(1)中, RMSE为均方根误差, y_max集样本最大值, y_min集样本最小值。

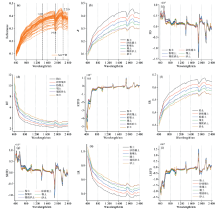
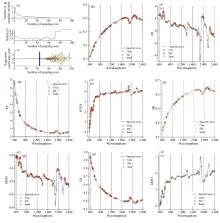
图3(a)和(b)显示了所有土壤样品和不同质地土壤的光谱经S-G平滑后的反射率变化趋势。 土壤原始光谱S-G平滑曲线变化规律大致相同, 反射率变化范围在0.05~0.5之间, 土壤反射光谱曲线存在相交现象, 交点主要集中于可见光波段。 在400~750 nm波段范围, 土壤的光谱反射率较低但变化率较快, 在400~1 300 nm范围, 光谱反射率随波长的增加而增加, 随后1 380 nm波段附近出现一个小吸收峰, 在1 400~2 300 nm波断之间, 有多个吸收峰和反射峰, 在2 150 nm波段附近反射率达到整体的最大值。 吸收峰和反射峰的位置几乎一致, 在1 400、 1 900、 2 200和2 350 nm波段附近存在不同强度的吸收带, 1 400和1 900 nm波段附近的吸收带是由于水中羟基(— OH)团的伸缩振动和矿物质中的水分子引起的, 而2 200 nm波段附近吸收带则是与黏土或者黏土矿物(AL-OH)的结构有关, 2 350 nm附近的吸收特征可能是有碳酸盐或者伊利石的存在[图3(a)]。

图3

Fig.3

Figure Option ViewDownloadNew Window

图3 土壤高光谱反射率曲线 (a): 全部土壤样本原始光谱S-G平滑; (b): 不同质土壤样本原始光谱S-G平滑; (c): 一阶微分; (d): 倒数; (e): 倒数一阶微分; (f): 平方根; (g): 平方根一阶微分; (h): 倒数之对数; (i): 倒数之对数一阶微分Fig.3 Soil hyperspectral reflectance curves (a): Spectral of all soil samples after S-G smoothing; (b): Spectra of different soil textures after S-G smoothing; (c): First derivative; (d): Reciprocal transformation; (e): Reciprocal transformation first derivative; (f): Square root; (g): Square root first derivative; (h): Logarithm of reciprocal; (i): Logarithm of reciprocal first derivative

图3(b— i)为原始光谱与不同光谱变换下的不同土壤质地光谱曲线。 在400~2 400 nm波段范围内粉土反射率最高, 砂土或壤质砂土反射率最低, 该现象与土壤颗粒表面粗糙程度有关, 随着土壤颗粒的增大, 导致土壤反射率一定程度的降低[图3(b)]。 对比图3(b— i)发现, 一阶微分变换光谱曲线[图3(c, e, g, i)], 土壤质地在可见光波段(400~760 nm)的区分程度更加明显, 在1 400、 1 900、 2 200和2 350 nm波段附近的吸收峰也得到增强。 图3(c, g)FD和SRFD变换在550、 680、 1 430、 1 930和2 220 nm波段附近粉土反射率最高, 在1 400、 1 900、 2 200和2 350 nm波段附近粉土反射率最低, 砂土在405和470 nm附近反射率最低, 在2 350 nm附近反射率最高。 图3(e)RTFD变换在430、 510和2 350 nm附近砂土差异突出, 反射率最低。

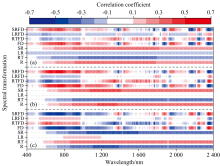
三种粒径含量与不同光谱变换后波段反射率的相关系数如图4所示, 黏粒含量和粉粒含量在不同光谱变换下的相关性总体表现一致, 砂粒含量呈现相反的趋势。 三种粒径含量不同光谱变换的强相关系数所在波段区间大致相同, 经过一阶微分光谱变换(FD、 RTFD和SRFD)后, 大部分波段相关性得到明显提升, 相关系数绝对值达到0.5以上的波段明显增加并且在可见光部分(400~760 nm)有所增强。 黏粒含量在FD变换中最大相关系数为-0.62(2 348 nm), RTFD变换和SRFD变换最大相关系数分别为-0.58(2 251 nm)和-0.60(2 348 nm), 粉粒含量在FD变换中最大相关系数为0.67(779 nm), RTFD变换和SRFD变换最大相关系数分别为0.63(2 348 nm)和0.70(730 nm), 砂粒含量在FD变换中最大相关系数为0.68(2 348 nm), RTFD变换和SRFD变换最大相关系数分别为-0.64(2 348 nm)和-0.70(760 nm)。 综合比较, 一阶微分变换是一种有效的处理高光谱数据的方法, 能够去除背景噪声和基线漂移, 解决光谱重叠问题, 进而提高光谱反射率与不同粒径含量之间的相关性。 高光谱数据具有丰富的波段信息, 但往往受到细节噪声和共线性等干扰。 为了克服这些干扰, 通常采用S-G平滑方法来减少噪声和不规则性, 同时利用一阶微分变换突显不同波段间的变化情况, 突显数据中凸起和凹陷的特征, 充分挖掘光谱信息^[8]。 FD、 RTFD和SRFD变换与粒径含量的最大相关系数绝对值达到0.58以上, 最高达到0.70, 结果证实了一阶微分变换在消除细节噪声干扰和解决光谱重叠问题上的有效性, 提高了光谱分辨率和灵敏度, 突显土壤光谱特征。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 三种粒径含量与不同光谱变换的相关性热图 (a): 黏粒含量; (b): 粉粒含量; (c): 砂粒含量Fig.4 Heat maps of the correlation between three particle size contents and different spectral transforms (a): Clay content; (b): Silt content; (c): Sand content

CARS算法设置的蒙特卡罗(MC)采样次数为100, 随着采样次数的增加, 样本选取的波段数、 RMSECV和各波段回归系数变化结果如图5(a)所示。 在指数衰减函数(EDF)作用下, 前10次采样变量快速减少, 随后逐渐减慢, 表明算法在变量选取中具有“ 粗选” 和“ 精选” 两个阶段。 采样次数达到44次时为最佳(OPT), 对应RMSECV达到最低点, 提取的特征波段数(N)为100, 仅为原始光谱波段数的5%, 极大压缩了数据量。 八种光谱变换的最佳采样次数和提取的特征波段数如表1所示, 筛选特征波段数为全波段数的1.05%~6.15%, Sand-SR提取的特征波段数最多为123个, Sand-LRFD提取的特征波段数最少为21个, 均可有效地降低了数据的冗余。 八种不同光谱变换下, CARS算法提取下不同粒径含量对应特征波段的位置如图5(b— i)。 不同光谱变换筛选出的特征波段数及位置存在差异。 R、 RT、 SR和LR变换所选的特征波段主要集中在800~1 200和1 600~2 400 nm范围, FD、 RTFD、 SRFD和LRFD变换选出的特征波段主要分布在400~700、 900~1 300、 1 500~1 700和2 200~2 400 nm范围, 所选波段的位置多集中在曲线拐点处。 一阶微分变换扩展了400~700 nm范围内的光谱有效信息, 减少了噪声干扰和无效信息的冗余。 不仅拓宽了CARS算法可选择波段的范围, 还能更充分地利用高光谱信息。

图5

Fig.5

Figure Option ViewDownloadNew Window

图5 不同光谱变换的CARS算法特征波段提取 (a): CARS筛选结果; (b): 原始光谱; (c): 一阶微分; (d): 倒数; (e): 倒数一阶微分; (f): 平方根; (g): 平方根一阶微分; (h): 倒数之对数; (i): 倒数之对数一阶微分Fig.5 Feature band extraction using CARS algorithm with different spectral transformations (a): CARS screening results; (b): Reflectivity; (c): First derivative; (d): Reciprocal transformation; (e): Reciprocal transformation first derivative; (f): Square root; (g): Square root first derivative; (h): Logarithm of reciprocal; (i): Logarithm of reciprocal first derivative

表1

Table 1

表1(Table 1)

表1 三种粒径含量下八种光谱变换的最佳采样次数和特征波段数 Table 1 Optimal sampling times and number of characteristic bands of eight spectral transforms for three particle size contents 类型 R FD RT RTFD SR SRFD LR LRFD OPT N OPT N OPT N OPT N OPT N OPT N OPT N OPT N Clay 44 100 57 40 48 75 51 61 58 37 47 81 46 87 58 37 Silt 46 87 53 53 59 35 52 57 56 43 55 46 47 81 57 40 Sand 44 100 51 61 65 23 46 87 41 123 46 87 48 75 66 21

表1 三种粒径含量下八种光谱变换的最佳采样次数和特征波段数 Table 1 Optimal sampling times and number of characteristic bands of eight spectral transforms for three particle size contents

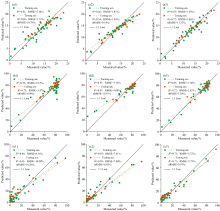
基于CARS算法筛选八种光谱变换的特征波段, 结合PLSR、 RFR和SVR三种模型, 分别进行黏粒、 粉粒和砂粒含量的估测。 共产生72种不同的结果, 如图6所示。 三种模型中, SVR模型估测三种粒径含量的效果最佳, 黏粒(SRFD-SVR)的训练集和测试集R²分别为0.83和0.72, RMSE分别为1.03%和1.86%, 粉粒(SRFD-SVR)的训练集和测试集R²分别为0.85和0.72, RMSE分别为2.74%和2.82%, 砂粒(RTFD-SVR)的训练集和测试集R²分别为0.73和0.71, RMSE分别为5.72%和5.75%。 八种光谱变换对比发现, 经FD、 SRFD、 RTFD和LRFD变换后, 模型精度均得到不同程度的提升, 其中SRFD和RTFD变换表现出色, 相较于黏粒(SR-SVR)训练集(R²=0.53, RMSE=2.64%)和测试集(R²=0.45, RMSE=3.47%)的结果, 黏粒(SRFD-SVR)训练集和测试集R²分别提升了0.3和0.27, 同时RMSE降低了1.61%, 测试集的nRMSE降低了9.8%。 一阶微分变换在提升土壤粒径含量估测模型的精度和稳定性方面起着关键性作用。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 八种光谱变换结合三种回归模型估测三种粒径含量结果Fig.6 Eight spectral transformations combined with three regression models for estimating three particle size contents

图7为三种粒径含量估测模型中最优光谱变换形式的实测值与预测值散点图。 其中, PLSR和RFR模型出现明显的偏移现象, 导致数据较为离散, 容易出现高估或低估现象。 相比较下, SVR模型测试集的R²较高, RMSE更低, 样点数值接近于1∶ 1线, 数据较为集中, 离散程度低, 表现出良好的估测效果。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同粒径含量的PLSR、 RFR和SVR最优模型实测值与预测值比较 (a1)— (a3): 黏粒含量; (b1)— (b3): 粉粒含量; (c1)— (c3): 砂粒含量Fig.7 Comparison of the measured and predicted values of the optimal models of PLSR, RFR and SVR for different particle size contents (a1)— (a3): Clay content; (b1)— (b3): Silt content; (c1)— (c3): Sand content

Shahrayini等^[16]采用RFR模型估算的砂粒含量R²为0.70, 黏粒含量R²为0.73, 黏粒含量估算的精度高于砂粒含量的精度, 并且均达到0.70以上, 与本研究的结果一致。 机器学习算法的应用为光谱建模提供了更为优越的解决方案, 显著提升了估测模型的精准度和稳定性水平^[19]。 土壤质地光谱反演过程中, 不同方法在构建模型时精度差别较大, Hobley等^[4]研究结果表明不同预测模型对不同粒径含量的估测精度的差异性, PLSR模型对黏粒和砂粒预测效果最好, RFR模型对粉粒预测效果较好。 Ludwig等^[20]比较了PLSR、 PLSR结合遗传算法(GA-PLSR)和SVR在印度班加罗尔耕地土壤属性估测中的有效性, PLSR对黏粒含量和砂粒含量的估测是有效的, 对粉粒含量的估测是无效的, 其中发现随机验证样本对黏粒含量的估测精度顺序为SVR> PLSR> GA-PLSR。 土壤属性存在时空上的异质性, 模型的适用性可能存在差异^[11]。 SVR和PLSR两种方法对噪声和异常数据影响较小, 并且在少量样本数据的情况下表现出更好的鲁棒性和泛化能力, 而RFR则需要更高的样本量来达到好的性能^[21]。 因此, SVR和PLSR模型精度总体高于RFR模型, 表现出良好的建模效果。 但由于样本数量较少的限制, 在模型适用性和研究结果等方面可能受到一定影响。