选取河北省安平县作为试验区, 该试验区的粮食作物以冬小麦、 夏玉米为主, 可为研究提供较好的实验场景。 选择品种为济麦22的种植田块开展研究, 田间实验分别于冬小麦扬花期、 灌浆期开展, 具体时间为2018年5月5日至6日、 5月23日— 25日。 选取面积较大的地块开展田间实验, 选择无病害(避免病害对植株光谱的影响)、 连续的冬小麦植株进行冠层光谱数据采集, 并获取植株样本。 冬小麦植株样本采集时, 先将冬小麦叶片进行分离, 并即刻利用精密电子秤测定叶片鲜重, 然后将样本置于保鲜袋内。 待全部田间样本采集完成后, 再利用烘箱对样本进行烘干处理。 待样本烘干后, 选用精密电子秤测定样本干重, 并结合田间测定的样本鲜重得到样本的含水量。

太阳的光照强度、 入射角等参量的改变也会对地物反射光谱曲线产生影响; 为避免光照强度、 入射角等参量对光谱数据采集产生影响, 选在10:00— 15:00进行冬小麦反射光谱的测定。 光谱测量设备为美国ASD生产的spectral4, 该设备能采集冬小麦冠层在350~2 500 nm内的反射光谱, 反射光谱的分辨率为1 nm。 冬小麦冠层光谱采集时, 采集人员面向太阳入射方向, 手、 背伸直, 将光谱收集探头置于冬小麦植株上方50 cm处, 待光谱稳定后开始采集, 每个实验小区采集10条反射光谱, 并取均值作为该实验小区的最终反射光谱。

光谱采集时易受大气内水汽、 气溶胶等组分的影响; 本实验数据采集于初夏, 此时期的区域温度较高, 作物蒸腾作用较强, 进而导致冬小麦冠层垂直上方的空气含有大量水汽及其他组分, 进而导致采集的冬小麦冠层光谱数据含有大量噪声。 光谱内的噪声信息与检测目标无关, 对光谱内的可用信息产生了较强干扰, 易导致模型稳定性较差, 因而需对冬小麦冠层光谱进行去噪处理。 采用长度为9的低通滤波器对光谱数据进行初步去噪处理, 并删除1 500~2 500 nm区间内失效的光谱数据。

作为一类重要的信号处理算法, 离散小波算法可将光谱数据分离为一系列高频信息与低频信息, 且每增加1分解尺度, 分离的高频信息与低频信息的光谱分辨率均降低1倍^[16], 其对光谱数据的分解过程如图1所示(图中, S为光谱数据; Hi是第i尺度的高频信息; Ai是第i尺度的低频信息)。 当前, 离散小波算法已逐步应用于光谱数据的去噪、 信息分离、 增强等处理与分析。 离散小波是一种无损信号处理算法, 其对光谱数据的处理是可逆的, 然而由离散小波算法分离的各尺度高频信息、 低频信息与原光谱信息的内在关联尚未明确, 无法为离散小波算法在光谱数据的噪声去除提供基础理论支撑。 为此, 以野外冬小麦冠层光谱数据与相应参量为数据源, 采用离散小波算法对冬小麦冠层光谱数据进行处理, 以探寻高频信息、 低频信息与原光谱信息的内在关系, 研发冬小麦冠层光谱噪声信息去除方法。

图1

Fig.1

	Figure Option ViewDownloadNew Window
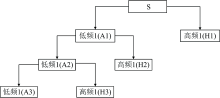	图1 基于离散小波算法光谱数据分解流程示意图Fig.1 Schematic diagram of spectral data decomposition based on discrete wavelet algorithm

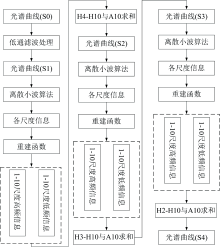
在深入理解离散小波算法分解光谱数据的机理基础上, 提出了基于离散小波算法光谱噪声去除方法, 具体流程如图2所示。 先采用离散小波算法对原光谱数据S0进行分解, 尺度为1— 10, 小波基为Meyer, 并求取H4— H10、 A10之和, 记为S1; 然后, 利用离散小波算法对S1数据进行分解, 尺度为1— 10, 小波基为Meyer, 并求取H3— H10、 A10之和, 记为S2; 最后, 离散小波算法对S2数据进行分解, 尺度为1— 10, 小波基为Meyer, 并求取H2— H10、 A10之和, 记为S3。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 光谱信息去噪技术路线图Fig.2 Roadmap of spectral information denoising technology

偏最小二乘算法是一种常用的多元回归分析算法, 兼有主成分分析算法、 相关分析算法、 线性回归算法等特点, 能有效减少参量间的共线问题。 截止目前, 偏最小二乘算法已广泛应用于作物理化参量的定量检测^[18]。 为客观评价本研究的效果, 选用偏最小二乘算法构建冬小麦叶片含水量估测模型。

为验证去噪方法的实用性, 采用偏最小二乘算法构建冬小麦叶片含水量估测模型, 并利用去噪前、 后估测模型精度作为评价。 2/3实验样本数据用于模型的构建, 剩余1/3实验样本用于模型的验证。 为客观评价模型的精度, 选用决定系数(R²)、 均方根误差(RMSE)对模型进行评价, 其计算公式如式(1)和式(2)所示

R2=1-∑i=1n(WCi-WCPi)2∑i=1n(WCi-WC¯)2(1)

$\text { RMSE }=\sqrt{\frac{\sum_{i=1}^{n}\left(W C_{i}-W C P_{i}\right)^{2}}{n}}$(2)

式(1)和式(2)中, WC_i是第i份样本冬小麦叶片含水量的实测值, WCP_i是估测模型对第i份样本的预测值, WC¯是全部样本实测值的均值。

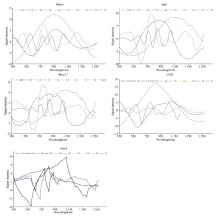
为探寻离散小波对光谱数据的分解规律, 分析各尺度信息与原光谱内在联系, 为研发基于离散小波算法光谱信息去噪方法提供基础理论支撑。 利用离散小波变化对冬小麦光谱数据进行分解, 分解尺度为10尺度, 小波基为Meyer; 然后将各分解尺度逐一重构, 并将A10与H1— H10进行逐尺度求和, 各尺度之和的曲线演变如图3所示, 其中绿线为去噪前光谱, 橙线为去噪后合并的光谱。 由图3可知, 随各分解尺度信息的逐步合并, 合并后的曲线图逐步复原至原冬小麦光谱的形态, 究其原因是离散小波算珐对光谱信息的分解是可逆的, 其光谱信息在分解过程中无损失。 从各合并后的曲线进行对比分析可知, 随分解尺度的逐步合并, 曲线局部大、 中、 小特征依次显现, 其中在将H8— H6合并后, 合并后的曲线已呈现冬小麦冠层光谱的整体轮廓, 其余尺度均仅能对合并曲线进行局部修正, 且修正幅度逐渐减弱。 H1— H3对合并曲线的影响甚少。 综上可知, 在离散小波算法下, 合并(光谱)曲线随合并尺度数的不断增加, 原光谱曲线的局部的大、 中、 小特征依次凸显, 且随H10— H1分解尺度的依次加入, 分解信息对合并曲线的修正幅度也逐步减弱, 其中, 依次将H3— H1后, 曲线几乎无变动。 由此可知, H3— H1尺度的高频信息仅保存原光谱内的微量信息, 无H3— H1尺度信息的光谱重构能较好的保留原光谱信息。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 基于离散小波各分解尺度信息之和的演化分析图Fig.3 Evolutionary analysis diagram of integrated information from various decomposition scales of discrete wavelet

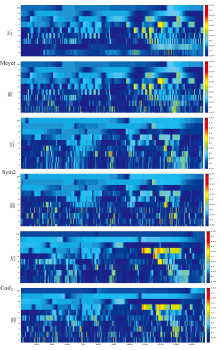
为探寻各小波基对光谱去噪信息的影响, 选用Coif2、 Db5、 Meyer、 Rbio3.7、 Sym2为小波基分别对光谱数据进行分解, 分解尺度为10尺度。 基于各小波基分解的光谱信息如图4所示, 由图4可知, 基于各小波基分解的各分解尺度信息整体随分解尺度的增加而增加; 基于各小波基分解的1— 10分解尺度信息的曲线形态均存在差异, 其中基于Meyer、 Db5、 Rbio3.7分解的1— 10分解尺度信息的整体形态均具有较强的相似性, 尤其是基于Meyer与Db5分解的1— 10分解尺度信息; 基于Coif2与Sym2分解的光谱信息的整体形态均具有相对较强的相似性。 综上可知, 基于小波基Meyer、 Db5、 Rbio3.7分解的1— 10尺度信息间具有较强的相似度, 基于Coif2与Sym2分解的光谱信息的整体形态具有相对较强的相似性, 基于两类小波基分解的光谱在形态上存在较大差异, 二者具有较强的互补性。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 基于离散小波算法光谱信息分离结果图 2.3 相关性分析Fig.4 Spectral information separation based on discrete wavelet algorithm

为研究分析去噪方法对光谱与冬小麦叶片含水量的相关性的影响, 利用离散小波算法对去噪前、 后的光谱数据进行处理, 并将处理后的光谱数据与冬小麦叶片含水量进行相关性分析。 图5为去噪前、 后的光谱经离散小波算法处理后, 1— 10分解尺度的高频信息与冬小麦植株叶片含水量的决定系数(R²)矩阵图, 横轴为波段长度(350~1 500 nm), 纵轴为分解尺度(1— 10)。 从图5可知, 去噪前位于1— 3分解尺度的高频信息对冬小麦叶片含水量的敏感性明显高于去噪后, 且敏感波段的分布也发生了明显变化; 去噪前位于1— 3尺度的敏感波段的分布呈离散化, 而去噪后则呈集中分布。 去噪前、 后位于4— 10尺度内的敏感波段的分布则无明显变化, 而高频信息对叶片含水量的敏感性却因小波基的选择而产生差异, 其中去噪后位于Coif2内的高频信息对叶片含水量的敏感性明显高于去噪前; 位于Sym内, 处于900 nm附近的敏感波段的敏感性则是去噪后的较强, 而处于1 290 nm附近的敏感波段的敏感性则是去噪前的较强; 究其原因是Sym2、 Coif小波基与Meyer小波基存在明显差异, 二者在光谱信息分离中存在明显差异, 有助于可用光谱信息的增强。 在Meyer小波基分析下, 去噪前、 后高频信息与叶片含水量的敏感性及敏感波段的分布无明显变化, 究其原因是光谱去噪、 分析均采用的Meyer小波基, 其对光谱的分解过程无变化所致, 表明本文提出的去噪方法能有效保留原光谱的主要信息。 综上可知, 在1— 3尺度内, 本方法降低了光谱对冬小麦叶片含水量的敏感性, 且改变了敏感波段的波段位置的分布情况。 在4— 10尺度内, 在小波基Coif2处理下, 本方法能明显提升光谱对冬小麦叶片含水量的敏感性; 在Sym2小波基处理下, 本方法可提升局部波段对冬小麦叶片含水量的敏感性; 在Meyer小波基分析下, 本方法能较好的保存了光谱的主要信息。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 噪声去除前、 后高频信息与冬小麦叶片含水量的决定系数(R2)矩阵图 2.4 基于各小波基构建冬小麦叶片含水量估测模型Fig.5 Determination coefficient (R2) matrix of high frequency information and leaf water content of winter wheat before and after noise removal

冬小麦叶片含水量在冠层反射光谱中的作用较强, 多为吸收特征, 而光谱数据经离散小波分解后, 其原光谱中的中-强吸收特征主要位于5— 7尺度。 位于1— 3尺度的光谱信息多为细节信息, 多受噪声信息的影响, 且其对原光谱信息的影响较小, 因而, 采用直接删除的方式进行处理。 先采用离散小波算法对原光谱数据进行分解, 尺度为1— 10, 小波基为Meyer, 并求取H4— H10、 A10之和, 记为S1; 然后, 利用离散小波算法对S1数据进行分解, 尺度为1— 10, 小波基为Meyer, 并求取H3— H10、 A10之和, 记为S2; 最后, 离散小波算法对S2数据进行分解, 尺度为1— 10, 小波基为Meyer, 并求取H2— H10、 A10之和, 记为S3。

由于去噪前、 后模型的建模精度均较高且差异不大, 因而从模型的验证精度进行对比分析, 评价本方法在提升模型精度方面的作用, 从建模精度与验证精度之差评价去噪方法对模型稳定性的提升作用。 从去噪前、 后模型验证精度的评价指标(R²)的分布图(图6)可知, 去噪后, 基于Meyer、 Sym2、 Coif2各分解尺度构建的估测模型的R²大多高于去噪前, 其中去噪后高于去噪前的模型约占模型总数的60%, 去噪前、 后变化不大的模型约占17%, 去噪后低于去噪前的模型约占23%。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 去噪前、 后模型验证精度评价指标(R2)的分布图Fig.6 Distribution of model validation accuracy evaluation metrics (R2) before and after denoising

研究表明本文提出的去噪方法能明显降低模型的估测误差, 提高模型的估测精度。 从去噪前、 后模型验证精度的评价指标(RMSE)的分布图(图7)可知, 基于Meyer、 Sym2、 Coif2各分解尺度构建的估测模型的RMSE大多低于去噪前, 去噪后RMSE低于去噪前的模型约占模型总数的43%, 去噪前、 后变化不大的模型约占23%, 去噪后高于去噪前的模型约占34%。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 去噪前、 后模型验证精度评价指标(RMSE)的分布图Fig.7 Distribution of model validation accuracy evaluation metrics (RMSE) before and after denoising

研究表明本文提出的去噪方法能明显提升估测模型的稳定性。 从去噪前、 后模型的建模精度与验证精度的评价指标(R²)之差(绝对值)的分布图(图8)可知, 基于Meyer、 Sym2、 Coif2各分解尺度构建模型的建模精度与验证精度之差大多低于去噪前, 其中去噪后低于去噪前的模型约占模型总数的77%, 去噪前、 后变化不大的模型约占7%, 去噪后高于去噪前的模型约占16%。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 去噪前、 后模型验证精度评价指标(R2)之差Fig.8 Difference between the evaluation metrics (R2) of model validation accuracy before and after denoising

研究表明本文提出的去噪方法能明显提升估测模型的稳定性, 降低建模、 验证的差异。 从去噪前、 后模型的建模精度与验证精度的评价指标(RMSE)之差(绝对值)的分布图(图9)可知, 基于Meyer、 Sym2、 Coif2各分解尺度构建模型的建模精度与验证精度之差大多低于去噪前, 其中去噪后低于去噪前的模型约占模型总数的73%, 去噪后高于去噪前的模型约占27%。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 去噪前、 后模型验证精度评价指标(RMSE)之差Fig.9 Difference between model validation accuracy evaluation indexes (RMSE) before and after denoising

前人多偏重于将小波算法作为光谱处理工具, 未能在小波算法处理分析光谱数据的机理进行分析, 进而导致针对小波算法在光谱数据处理中的应用仍停留在表面^{[18, 19]}; 然而针对基于小波变换在去噪和光谱数据挖掘方面的研究相对较少, 且缺乏相关基础理论的支撑。 受区域地理环境、 气候条件及气象因子等的影响, 野外采集的光谱数据受外界因子干扰的程度不同, 其内含的噪声量也存在差异, 而研究多偏用信噪比高的光谱数据, 少用质量较差的光谱数据, 进而导致相关研究成果的实际应用性不强^{[20, 21]}。 为研究分析离散小波算法对光谱数据的分解机理, 探寻基于离散小波算法光谱噪声信息去除与光谱处理方法, 本研究以冬小麦冠层光谱与叶片含水量为数据源进行实验, 并提出基于小波算法的光谱噪声去除与数据挖掘方法既能有效去除噪声信息对可用光谱信息的干扰, 提升光谱数据对冬小麦叶片含水量估测的稳定性, 又可保持、 提升光谱对冬小麦叶片含水量的估测能力。 本方法能明显提高Sym2、 Coif2小波基对光谱数据的分解效果, 提升光谱对冬小麦叶片含水量的估测能力。 然而, 本方法未能提高Meyer小波基对光谱数据的分离效果, 未能有效提升光谱对冬小麦叶片含水量的估测能力, 究其原因主要是在去噪过程中, 采用小波基是Meyer, 且直接将H1— H3内的高频信息删除, 这导致再次采用Meyer对光谱数据进行分离时, 其H1— H3需从其他分解尺度中的数据中进行分离信息, 进而导致Meyer小波基未能有效提升光谱对冬小麦叶片含水量的估测能力。 这也表明干扰目标光谱信息的噪声并非全部来自水汽、 气溶胶等大气组分, 也受采用的光谱处理方法的影响。

解析了离散小波算法对光谱数据的处理机理, 可为离散小波算法在光谱处理中的应用方法探索提供基础理论支撑, 完善了离散小波应用于光谱数据处理的理论体系; 但本研究提出的光谱噪声去除与分析方法仅适用于对光谱吸收作用较强的地物指标, 例如植株含水量、 叶绿素等, 而不适用于弱光谱响应的地物指标的估测, 例如有机质含量偏低的耕层土壤, 叶片氮含量; 究其原因主要是本研究采用的是逐步去除H1— H3信息的方式进行去噪处理, 进而导致局部细节信息的消失, 因而不适用于含量较低的地物组分的研究。

尽管本研究在解析离散小波分离机理的基础上, 提出了光谱去噪方法, 但仍存在不足, 需进一步开展如下研究:

(1)如何对分离的光谱信息进行二次组合, 实现光谱信息的二次重构, 提升光谱信息的信噪比, 提高光谱对地物信息的估测能力, 仍需进一步实验、 分析。

(2)本方法局限在对于光谱响应较强的地物组分的估测研究, 而针对含量较低的地物组分的估测研究尚未开展, 因而仍需进一步深入研究。