GPR是采用高斯过程先验对数据进行回归分析的一种机器学习方法, 采用GPR处理天文数据已取得诸多成果: Rajpaul等^[12]运用GPR对RV时间序列进行了分析; Pass等^[13]运用GPR估计系外行星的有效温度。 采用GPR对恒星光谱进行处理, 利用各个流量值之间的相关性, 计算各个流量值的均值和方差, 减小流量值的误差, 从而得到更加准确的光谱数据。

由于噪声的影响, 任意一段光谱的每个流量值被视为一个随机变量, 观测光谱表示为多个随机变量的联合分布

f~N(μ(λ), K(λ, λ))(1)

式(1)中, λ 表示波长, f代表光谱在λ 处的流量值, N表示高斯分布, μ (λ )代表均值函数, K(λ , λ )为协方差矩阵, 矩阵中的元素代表各个流量值之间的协方差。 给定一个波长λ _* , 光谱在λ _* 处的流量值为f_* , 它与现有观测数据f的联合分布为

ff* ~Nμ(λ)μ(λ* ), K(λ, λ)K(λ, λ* )K(λ* , λ)K(λ* , λ* )(2)

基于式(2), 以及光谱的流量值f, 可以计算f_* 的均值和方差

E[f* ]=μ(λ* )+K(λ* , λ)K-1(λ, λ)[f-μ(λ)](3)

var[f* ]=K(λ* , λ* )-K(λ* , λ)K-1(λ, λ)K(λ, λ* )(4)

采用GPR处理光谱数据时, 为了便于计算, 均值函数的值被设定为0, 协方差矩阵中的元素通过核函数计算得到, 常用的核函数有指数核函数、 周期核函数和Maté rn核函数等。 对于恒星光谱数据, 选择Maté rn核函数计算协方差矩阵中的元素值, 核函数如式(5)所示

k(λ, λ')=h21+τρ+τ23ρ2exp-τρ(5)

式(5)中, $\tau=\sqrt{5\left(\lambda-\lambda^{\prime}\right)^{2}}$, ρ 与h为超参数。 每一条恒星光谱的RV各不相同, 每一条光谱中的各段受到的污染也各不相同, 为了更加准确地建立各段光谱的模型, 核函数中的ρ 与h并没有确定, 对每段光谱需要求解对应的值。 Williams等^[14]采用似然函数最大化的方式求解核函数中的超参数, 本文使用相同的方法针对每一段光谱计算得到最佳的ρ 与h, 对数似然函数如式(6)所示

logL=-M2log2π-12logK-12fT(K)-1f(6)

式(6)中, M为每段光谱中的样本点个数。 由于观测光谱数据存在噪声, 在计算协方差矩阵时需要考虑这一因素, 此时的协方差矩阵为

C(λ, λ)=K(λ, λ)+diag(σ2)(7)

式(7)中, diag(σ ²)表示对角矩阵, 对角线元素为各个流量值的噪声方差。

随着天文观测技术的不断发展, 天文台获得了大量的恒星光谱数据, 对大量数据进行处理是GPR所面临的挑战。 针对这一问题, 需要对GPR算法进行一定的优化, 优化方案主要包括子集近似法、 稀疏内核法和低秩近似法^[15]。 子集近似法的实现原理是从全体的训练数据中抽取若干样本构成数据子集, 采用数据子集代替全体数据进行训练, 从而降低算法的计算复杂度^[16]。 当原始数据样本足够多时, 采用子集近似法对GPR进行优化可以在保证一定准确度的前提下降低GPR的计算复杂度。 但是采用该方案对GPR进行优化无法获得准确的方差。 稀疏内核法指的是当|λ _i-λ _j|超过某一阈值时, 将k(λ _i, λ _j)设定为0, 通过这种方式降低计算复杂度。 采用稀疏内核的方式降低GPR的计算复杂度会导致最后得到的协方差矩阵为半正定矩阵, 影响GPR算法的后续流程。 低秩近似法指的是将原始的协方差矩阵转换为低秩矩阵的乘积

K˜=KnmKmm-1KTnm(8)

从原始数据中选取m个样本点, 利用核函数计算得到K_mm, 然后利用全体数据和被抽样的数据子集计算K_nm, 根据式(8)计算 K˜代替协方差矩阵K_nn。 典型的低秩近似算法是Nyströ m^[17]。 当选取的样本子集过小时, Nyströ m算法的准确性较差, 而且会出现预测方差为负的情况^[14]。

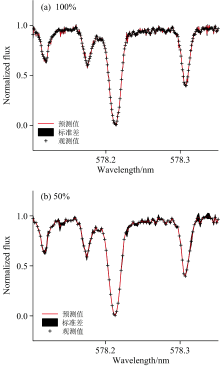
为了降低采用GPR处理光谱数据的计算复杂度, 同时确保计算得到的各个流量值的方差为正值, 本文采用子集近似法对光谱建模过程进行优化。 图1对比了采用随机抽取的50%样本数据实现光谱建模和利用全部数据实现光谱建模的效果。 从图1中可以看出: 二者的预测值相似, 使用部分样本点进行光谱建模在一定程度上增加了各个流量值的标准差, 但这种变化基本可以忽略不计, 对后续的RV计算影响较小。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 采用部分数据实现光谱建模Fig.1 Establish model of spectrum using partial data

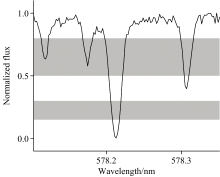
注意力机制是机器学习中一个热门概念, 它指的是针对输入数据中的不同部分, 赋予不同的权重, 从而得到更加准确的输出结果。 为了充分提取恒星光谱中所蕴含的RV信息, 注意力机制的思想被运用到本文的RV计算方法中: 一个观测光谱被看作多个部分光谱的叠加, 不同部分光谱的吸收线的相对深度处于不同的范围, 利用相似性函数计算不同部分光谱和原始观测光谱的相似性, 为不同的部分光谱分配权重。 在采用GPR算法处理光谱数据后, 根据各个流量值的均值提取恒星光谱中的吸收线。 选取相对深度大于0.2的吸收线, 将相对深度处于不同范围的吸收线分配至不同部分的光谱中。 图2展示了一个光谱分割的例子: 提取光谱中的吸收线, 将顶点处于同一区域的吸收线分割至同一个部分光谱中。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 吸收线提取示意图Fig.2 Diagram of extracting absorption lines

下一步是计算不同部分光谱的权重。 各个部分光谱所包含的吸收线数量各不相同, 在计算权重时需要考虑吸收线的数量和吸收线的相对深度。 根据流量值的均值完成对观测光谱的分割后, 计算每一条部分光谱的权重

wi(t)p=exp-1-zn(9)

式(9)中, z为每条部分光谱中吸收线相对深度的最小值, n为每条部分光谱中吸收线的数量。

采用视向速度法寻找系外行星, 会依据RV的变化情况, 结合其他信息判断是否存在系外行星。 本文通过求解恒星在不同时刻的Δ RV计算恒星的RV。

在上一部分中, 提取出每一段光谱中相对深度大于0.2的吸收线, 根据相对深度的不同, 利用提取出的吸收线构造了P个部分光谱。 选取分别从第i条光谱和第j条光谱的第t段中提取出的两个部分光谱, 它们所包含的吸收线的相对深度处于同一范围内, 对第j条光谱的第t段中第p个部分光谱的波长 λj(t)p进行处理

$\lambda_{j(t)}^{p}(v)=\lambda_{j(t)}^{p} \sqrt{\frac{1+v / c}{1-v / c}}$(10)

式(10)中, c为光速, v为速度。 采用最大似然估计算法计算两个部分光谱之间的视向速度差Δ R Vij(t)p, 对数似然函数如式(11)所示

logLij(t)p=-D2log2π-12log|Cij(t)p|-

12(rij(t)p)T(Cij(t)p)-1rij(t)p(11)

式(11)中, λij(t)p=[( λi(t)p)^T, ( λj(t)p(v))^T]^T为长度为D的列向量, fij(t)p=[( fi(t)p)^T, ( fj(t)p)^T]^T表示两个部分光谱实际观测到的流量值, rij(t)p表示实际观测数据与均值函数之间的残差。 针对 λij(t)p中的每一对波长点, 利用式(5)与式(7)计算得到 Cij(t)p中的元素值, 令对数似然函数取得最大值的v即为两条部分光谱之间的Δ R Vij(t)p。

按照上述步骤对所有光谱数据进行处理, 从而得到从任意两条光谱的相同段中提取出的第p个部分光谱之间的视向速度差Δ R Vij(t)p。 为了更加准确地描述采用不同部分光谱计算得到的视向速度差, 可以采用蒙特卡洛算法计算视向速度差的方差: 每一段观测光谱可以用均值函数和协方差矩阵描述, 根据这些信息生成多个模拟光谱, 利用生成的模拟光谱代替在视向速度差计算过程中的实际观测数据, 重复上述步骤, 得到多个结果后计算其均值和方差, 即可得到第i条和第j条光谱的第t段的两个部分光谱之间的视向速度差Δ R Vij(t)p及其方差σ (Δ R Vij(t)p)²。

每个部分光谱相对于各自的光谱具有不同的权重, 视向速度差涉及到不同光谱之间的计算, 接下来计算不同光谱对在相同波长段之间的视向速度差Δ RV_ij(t), 以及它们各自的方差σ (Δ RV_ij(t))²

ΔRVij(t)=∑p=1Pwi(t)p+wj(t)p∑q=1P(wi(t)q+wj(t)q)ΔRVij(t)p(12)

$\sigma\left(\Delta R V_{i j(t)}\right)^{2}=\sum_{p=1}^{P}\left[\frac{w_{i(t)}^{p}+w_{j(t)}^{p}}{\sum_{q=1}^{P}\left(w_{i(t)}^{q}+w_{j(t)}^{q}\right)}\right]^{2} \sigma\left(\Delta R V_{i j(t)}^{p}\right)^{2}$(13)

每条观测光谱由多段光谱组成, 为进一步提高Δ RV的准确性, 需要对这些结果进行处理。 在利用同一对观测光谱的不同波长段数据求得多个Δ RV及其方差后, 基于方差进行加权求和

ΔRVij=∑t=1TσΔRVij(t))-2∑k=1Tσ(ΔRVij(k))-2ΔRVij(t)(14)

$\sigma\left(\Delta R V_{i j}\right)^{2}=\frac{1}{\sum_{t=1}^{T} \sigma\left(\Delta R V_{i j(t)}\right)^{-2}}$(15)

即可得到每对光谱间的Δ RV。 最后, 利用所求的Δ RV计算恒星在不同时刻的RV及其方差, 如式(16)和式(17)所示

RVi=1S∑j=1SΔRVij(16)

$\sigma\left(R V_{i}\right)^{2}=\frac{1}{S^{2}} \sum_{j=1}^{S} \sigma\left(\Delta R V_{i j}\right)^{2}$(17)

按照上述步骤对所有恒星光谱进行处理, 即可计算恒星在不同时刻的RV。

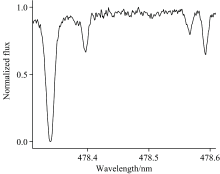
从欧洲南方天文台获取同一目标的多条光谱, 将观测光谱对齐叠加得到模板光谱, 对模板光谱的轮廓进行一定的修改得到一条模拟光谱。 假设RV的变化周期为20 d, 振幅为15 m· s^-1, 对模拟光谱进行多普勒频移, 得到1 000条光谱, 根据信噪比为多普勒频移后的光谱添加噪声, 得到最终的观测数据。 图3是令RV为0 m· s^-1生成的一条模拟光谱中的一部分。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 部分模拟光谱示意图Fig.3 Part of simulated spectrum

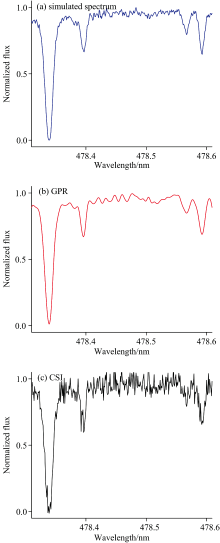
在得到观测样本后, 对比了采用GPR算法与三次样条插值(cubic spline interpolation, CSI)算法实现光谱连续化的结果, 如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 连续化光谱示意图Fig.4 Diagram of continued spectra using different methods

从图4中可以看出, 采用GPR算法处理后的观测光谱数据的流量值的均值函数相较于直接利用CSI算法处理的光谱数据, 前者的处理结果能够更加准确地反映光谱的变化情况, 与没有噪声的模拟光谱更加相似。

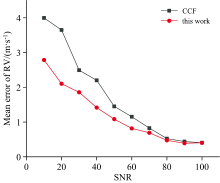
图5比较了在不同信噪比的情况下, 分别采用CCF和本文所提出的RV计算方法针对所有观测样本计算得到的RV的平均误差。 从图5中可以发现, 当模板光谱与恒星光谱不是完全匹配时, 数据驱动算法充分体现其优越性, 在信噪比较低的情况下, 采用本文算法计算的RV的平均误差明显低于采用CCF计算的RV的平均误差。 随着信噪比的增加, 两种算法的平均误差均会下降。 当信噪比大于70时, 两种算法均可达到较高准确度, 此时它们的误差基本一致。 本文所提出的RV计算方法能够充分提取相对深度较大的吸收线中的RV信息, 而且不会受到模板光谱和观测样本是否一致的约束, 当信噪比较低时可以实现较高的计算准确度。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同信噪比下RV的平均误差Fig.5 Mean error of RV at different SNR

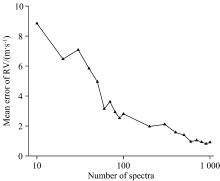
采用本文所提出的RV计算方法提取RV还需要考虑观测光谱数量与RV计算误差之间的关系。 图6给出了在信噪比为50的条件下, RV平均误差与观测光谱数量之间的关系。 可以发现, 随着光谱数量的增加, RV的平均误差逐渐减小, 当观测样本数量达到600时, 继续增加观测光谱数量无法减少平均误差, 此时的误差达到稳定状态。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同光谱数量的RV误差Fig.6 Mean error of RV at different number of spectra

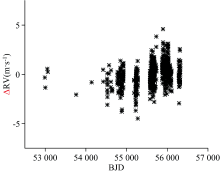
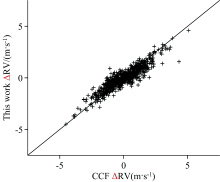
HD85512是HARPS-GTO项目的一个观测目标, 它的光谱类型是K5V, 根据目前的研究, HD85512的周围仅有一颗行星围绕, RV的振幅变化很低, 是一个十分简单的行星系统^[18]。 从欧洲南方天文台获取了700条HD85512的观测光谱, 采用本文提出的算法计算RV, 结果如图7所示。 将计算结果与采用CCF计算得到的RV进行比较 (为了方便比较, 采用CCF计算得到RV后, 所有的RV减去均值, 使采用CCF计算的RV与采用本文的算法所取得的结果处于相同的范围内), 如图8所示。 图8中的纵轴代表采用本文算法计算得到的RV, 横轴表示采用CCF计算得到的RV, 这些点基本分布在y=x这条直线附近。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 采用本文算法计算的RVFig.7 RV of this work

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 采用CCF与本文算法计算RV的对比Fig.8 Comparison of RV between CCF and this work

表1比较了采用不同算法计算得到的RV的rms。 从表1中可以看到, 采用CCF和TERRA计算得到的RV的rms基本一致, 而采用本文的算法计算得到的RV的rms相较于其他算法有一定的下降, 这意味着采用本文的算法从光谱中提取RV可以得到更加准确的结果。

表1

表1

表1 采用不同算法获取的RV的rms Table 1 rms of RV by different methods 算法名称 CCF TERRA this work rms/(m· s-1) 1.31 1.33 1.10

表1 采用不同算法获取的RV的rms