引用本文
黄晓红, 刘晓辰, 刘艳丽, 宋超, 孙永长, 张庆军. 便携式LIBS结合SSA-KELM的废钢成分定量分析方法[J]. 光谱学与光谱分析, 2024,44(9): 2412-2419.
HUANG Xiao-hong, LIU Xiao-chen, LIU Yan-li, SONG Chao, SUN Yong-chang, ZHANG Qing-jun. Element Detection in Scrap Steel Using Portable LIBS and Sparrow Search Algorithm-Kernel Extreme Learning Machine (SSA-KELM)[J]. Spectroscopy and Spectral Analysis, 2024,44(9): 2412-2419.
Doi:10.3964/j.issn.1000-0593(2024)09-2412-08  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
便携式LIBS结合SSA-KELM的废钢成分定量分析方法
黄晓红1,2, 刘晓辰1,2, 刘艳丽3,*, 宋超1,2, 孙永长1,2, 张庆军4
1.华北理工大学人工智能学院, 河北 唐山 063210
2.河北省工业智能感知重点实验室, 河北 唐山 063210
3.河钢集团钢研总院, 河北 石家庄 050000
4.华北理工大学综合测试分析中心, 河北 唐山 063210
*通讯作者 e-mail: liuyanli01@hbisco.com

作者简介: 黄晓红,女, 1973年生,华北理工大学人工智能学院教授 e-mail: tshxh@163.com

收稿日期: 2023-02-28 修回日期: 2023-10-10
基金: 国家自然科学基金区域创新发展联合基金重点项目(U21A20114),河北省高等学校科学技术重点研究项目(ZD2020152)资助
摘要

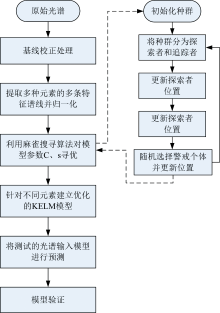
废钢是电炉炼钢的重要原料, 为有效利用废钢, 需对废钢中各元素进行检测。 提出了麻雀搜索算法优化的核极限学习机(SSA-KELM)与激光诱导击穿光谱技术(LIBS)相结合的新方法, 对中低合金钢和低合金钢的钢样共12组样品进行元素含量建模分析。 首先通过便携式LIBS光谱仪采集两类共计12种不同的废钢样品在170~400 nm范围内的激光诱导击穿光谱数据, 为降低实验波动影响, 每个试验样品的表面均匀选取28个不同的位置进行检测, 使用 K值校验剔除粗大误差, 并将剩余数据进行平均处理, 最终得到12个样品共336组平均光谱数据; 然后对获得的光谱数据进行基线校正和归一化处理, 降低基线波动影响; 然后选出待检测元素的多条相关谱线共65条作为模型的输入特征, 接着对光谱数据进行训练集与测试集的划分, 从每类钢种中随机选择一个样品, 提取其处理后的光谱数据作为模型的测试集, 剩余数据作为模型的训练集, 利用麻雀搜索算法(SSA)对核极限学习机(KELM)进行参数寻优, 针对相关元素进行建模。 最终所建立的C、 Cu、 Mn、 Cr、 Ni、 Si、 V、 Al、 Ti元素的模型在验证集的相关决定系数( R2)和均方根误差(RMSE)平均为0.996和0.016。 实验比较了单变量校正模型和基于遗传算法优化的核极限学习机(GA-KELM)的多变量校正模型的定量分析效果, 结果表明, 与单变量校正模型和遗传算法和核极限学习机(GA-KELM)模型相比, SSA-KELM模型的所有指标都有显著提高, 作为多变量模型的KELM与麻雀搜索算法相结合, 能够有效的减弱多种因素对待分析元素的干扰, 增强定量分析的性能, 通过与便携式LIBS系统结合, 可用于现场作业, 实现对废钢中各元素含量的快速精准检测。

关键词: 激光诱导击穿光谱; 废钢; 麻雀搜索算法; 核极限学习机; 定量分析
中图分类号:O433.4 文献标志码:A
Element Detection in Scrap Steel Using Portable LIBS and Sparrow Search Algorithm-Kernel Extreme Learning Machine (SSA-KELM)
HUANG Xiao-hong1,2, LIU Xiao-chen1,2, LIU Yan-li3,*, SONG Chao1,2, SUN Yong-chang1,2, ZHANG Qing-jun4
1. College of Artificial Intelligence, North China University of Science and Technology, Tangshan 063210, China
2. Hebei Key Laboratory of Industrial Intelligent Perception, Tangshan 063210, China
3. Physical and Chemical Testing Center of Material Technology Research Institute of HBIS Group Co., Ltd., Shijiazhuang 050000, China
4. Comprehensive Test and Analysis Center of North China University of Science and Technology, Tangshan 063210, China
*Corresponding author
Abstract

Elemental content detection is necessary for efficiently utilizing scrap steel, an important raw material for electric furnace steelmaking.In this study, a new method combining the sparrow search algorithm optimized kernel extreme learning machine (SSA-KELM) and laser-induced breakdown spectroscopy (LIBS) was proposed to analyze and model the element contents of 12 groups of steel samples, including medium-low alloy steel and low alloy steel. First, the portable LIBS spectrometer was used to collect laser-induced breakdown spectroscopy data of 12 different steel scrap samples in the range of 170~400 nm, and 28 different locations on the surface of each sample were selected for detection to reduce experimental fluctuations. The k-value check was used to eliminate gross errors, and the remaining data was averaged to obtain 336 groups of average spectrum data from 12 sample groups. Then, the obtained spectral data was subjected to baseline correction and normalization to reduce the baseline fluctuation. Multiple related spectral lines of the target elements were selected as the input features of the model, and the spectral data was divided into training and testing sets. A random sample from each steel type was selected as the model's testing set, and the remaining data was used as the model's training set. The sparrow search algorithm was used to optimize the parameters of the kernel extreme learning machine (KELM), and the model was established for the related elements. The final model for C, Cu, Mn, Cr, Ni, Si, V, Al, and Ti elements had an average correlation coefficient ( R2) and root mean square error (RMSE) of 0.996 and 0.016, respectively, on the validation set. The quantitative analysis performance of the single variable calibration model and the genetic algorithm optimized KELM (GA-KELM) multivariate calibration model were compared, and the results showed that the SSA-KELM model had significant improvements in all indicators compared to the single variable calibration model and GA-KELM model. The combination of KELM and Sparrow search algorithm as a multivariate model can effectively reduce the interference of multiple factors on the target elements and enhance the performance of the quantitative analysis. It can rapidly and accurately detect various element contents in steel scrap on-site by combining it with the portable LIBS system.

Keyword: Laser-induced breakdown spectroscopy; Scrap steel; Sparrow search algorithm; Kernel extreme learning machine; Quantitative analysis
引言

钢铁拥有良好的综合力学性能, 能够依靠其韧性和塑性加工成任何形状, 凭借低廉的价格和可靠的质量成为世界上被最为广泛使用材料之一。 但伴随着钢铁的大量生产和使用, 废钢的产生也是不可避免的, 人们对于废钢的回收工作也做了大量的努力[1], 使得废钢的回收率大大提高。 在全社会倡导节能减排的背景下, 如何更好的回收和使用成为了我们迫切解决的问题[2]。 在钢铁生产中对废钢的有效利用, 是钢铁行业需要着重发展的环节之一。 废钢被回收后, 通常也会作为主要原料之一重新用于钢铁的冶炼生产, 使用废钢进行钢铁的冶炼不仅环保节能, 节省了大量的资源, 还能获得更好的冶炼效果。 废钢主要用于短流程电炉炼钢, 作为主料使用, 或在长流程转炉炼钢中作为添加料使用, 对钢铁企业的转型及可持续发展也具有积极的推动作用, 在未来钢铁的发展中占据着重要地位。 废钢被用于炼钢之前, 要对废钢进行合理的分类, 废钢中元素含量检测是钢铁行业中对废钢进行分类再利用的重要步骤, 通常是获取钢的光谱对各进行元素分析。 在传统的废钢元素检测方法中, 火花直读[3]、 红外光谱法[4]和X荧光检测法[5]等方法被广泛应用。 然而, 传统的火花直读与红外光谱法需要对样品进行研磨、 熔融等复杂的制备步骤, 且需要较高标准的实验环境, 不仅耗时耗力, 而且检测仪器也不利于工人进行现场作业, 减缓了炼钢流程。 X荧光检测法作为一种成熟的分析技术, 虽然具有样品制备简单, 速度快等优点, 但对于碳元素等一些低浓度轻元素的测量分析有限制, 对含碳钢材或低合金钢材的检测分析效果不佳。 随着光谱技术的进步, 激光诱导击穿光谱技术(laser-induced breakdown spectroscopy, LIBS)应运而生。 基于激光诱导等离子体可以对各种物质进行元素分析, 而且不论物质的状态是固态、 液态、 气态还是胶体态, 都可以激发产生等离子体, 利用光谱仪收集获得等离子体光谱。 相较于传统方法, LIBS技术无需复杂的样品制备步骤, 操作简便, 适用于现场操作, 同时可测量低浓度的轻元素, 如铝、 硅和碳元素等, 可以轻松对不锈钢、 低合金和碳钢材料进行分析, 进而加速炼钢流程。 由于LIBS光谱包含各元素强度与含量的相关信息, 分析人员可以根据特征发射线的波长和强度对目标样品的化学组成进行定性和定量分析。 LIBS作为一种光谱化学技术, 从诞生以来就不断发展和进步, 目前已经应用于地质、 冶金、 农业、 航天和医学[6, 7, 8, 9, 10, 11, 12]等多种行业。 近年来, 对于小型化LIBS的研究和发展也使得这一技术更加普及和高效[13]。

使用LIBS技术对待测样品中的元素定量检测, 需要对获取的LIBS光谱数据预处理并利用预测模型进行分析。 对于分析模型, 分为单变量校正模型和多变量校正模型两类。 单变量校正方法是用一条元素谱线分析元素的相关信息, 最有代表性的单变量分析方法为内标法。 内标法作为快速高效的理论方法, 在工业中被广泛使用, Sheng等[14]基于LIBS技术利用内标法对铁矿石中的铁进行分析, 首先计算出等离子体温度与电子数密度, 保证其满足局部热力学平衡状态, 基于此选择Si 405.52 nm作为内标线对四条Fe线建立定标曲线并与标准加入法进行比较, 结果显示以内标法作为定量分析方法能够应用于钢铁行业, 进行质量保证和控制。 Zhu等[15]首次使用LIBS结合内标法测量甘草中的有害微量元素, 并与免校准LIBS(CF-LIBS)进行了对比, 得到了更好的结果, RE达到2.19%, 用时低于0.3 h, 均优于CF-LIBS的检测结果, 为快速和准确的检测甘草中的有害元素提供了更新的思路。 这些研究表明了使用单变量方法结合LIBS进行元素分析的可行性。 对于待测元素来说, 与其相关的特征谱线分布在整个光谱中的多个特定波长, 并且由于样品本身的特性, 会使其产生基体效应和自吸收效应, 仪器的参数波动也会对数据造成一定的影响。 这些综合起来的波动无法用精确的数学形式表达, 使得仅仅利用单变量分析方法很难更加精准地进行分析预测。 多变量分析成为更加有效的方法, 多变量模型能够综合多个变量的优势, 充分利用LIBS光谱中所包含的信息, 弱化噪声带来的不稳定性, 从而更精确地对样品进行分析。 随着机器学习的发展, 研究人员将其逐渐应用于LIBS分析中。 Rifai K等[16]将LIBS与机器学习模型结合, 针对铜镍矿石样品中的Mg, Ni等6种元素进行检测分析。 首先对32个样品划分训练集和校正集, 使用单变量分析方法进行建模与预测, 并分析了干扰和不稳定性的存在, 随后使用偏最小二乘法(PLS)进行参数优化和建模, 最终的预测误差远低于单变量分析结果, 证明了利用PLS方法的进行对铜镍矿石进行预测是一种更有效的定量分析方法。 郭志卫等[17]为了检测水泥粉末成分, 建立偏最小二乘法(PLSR)和支持向量机回归(SVR)两种模型进行分析, 对水泥中元素的测试结果表明, SVR模型在验证集上的R2达到0.99, 整体优于PLSR, 并对可行性做出了分析。 多变量分析的非线性拟合能力在定量分析中具有显著优势。 梅亚光等[18]利用遗传算法优化的KELM模型对高合金钢和低合金钢中的元素进行定量检测并与PLS模型进行对比。 最终Si、 Mn、 Cr、 Ni、 V、 Ti、 Cu、 Mo元素的预测均方根误差分别为0.24%、 0.16%、 0.06%、 0.07%、 0.22%、 0.04%、 0.07%、 0.04%。 实验表明该方法训练速度快、 模型的泛化性能高, 无需人为调参, 在校正基体效应方面效果优于传统定标法以及PLS模型。 这些研究都表明了多变量分析方法与LIBS技术结合能够很好的针对样品中的元素进行准确稳定的分析, 同时也在不断发展和稳步提高中, 拥有无限可能。

提出了一种使用麻雀搜索算法优化的核极限学习机方法(SSA-KELM)对钢铁样品中的Cu、 Si、 Ti等多种元素进行分析。 首先利用预处理方法对LIBS光谱进行处理, 使光谱数据变得稳定, 再结合麻雀搜索算法优化的核极限学习机对12种钢样进行建模分析, 针对钢中不同元素分别建立了多元校正分析模型, 同时建立了内标法与基于遗传算法优化的核极限学习机分析模型作为对比。 KELM具有优秀的非线性拟合能力和泛化性能, 使得预测结果更加准确; 由于麻雀搜索算法的快速寻优能力, 也使得在建模过程中避免了复杂的参数寻优过程, 大大节省了建模时间。 结果表明, 建立的SSA-KELM模型预测效果较好, 通过与便携式LIBS相结合, 能够实现钢铁企业在现场对废钢含量进行快速分析, 实现对废钢的实时高效利用。

1 相关原理
1.1 核极限学习机

极限学习机(ELM)是Huang等在2006年提出的算法[19]。 它是一种针对单隐含层前馈神经网络(single-hidden layer feed forward neural network, SLFN)的算法, 由输入层、 单隐含层和输出层组成。 相对于传统前馈神经网络训练速度慢, 容易陷入局部极小值点, 学习率的选择敏感等缺点, ELM算法随机产生输入层与隐含层的连接权值及隐含层神经元的权值, 且在训练过程中无需调整, 只需要设置隐含层神经元的个数, 便可以获得唯一的最优解。 与之前的传统训练方法相比, ELM网络的主要优点是通过随机设置隐含层的输入结点的权值来改善反向传播, 具有学习速度快, 泛化性能好等优点。

KELM算法[20]是受支持向量机原理的启发, 将核函数引入到ELM中。 KELM能够在保留ELM优点的基础上提高模型的预测性能。 ELM是一种单隐含层前馈神经网络, 其学习目标函数F(x)可用矩阵表示为

F(x)=h(x)×β=H×β=L(1)

式(1)中, x为输入向量, h(x)、 H为隐藏层节点输出, β 为输出权重, L为期望输出。

将网络训练变为线性系统求解的问题, β 根据β =H* L确定, 其中, H* 为H的广义逆矩阵。 为增强神经网络的稳定性, 引入正则化系数C和单位矩阵I, 则输出权值的最小二乘解为

β=HTHHT+IC-1L(2)

引入核函数到ELM中, 核矩阵为

ΩELM=HHT=h(xi)h(xj)=K(xi, xj)(3)

式(3)中, xi, xj为试验输入向量, 则可将式(1)表达为

F(x)=[K(x, x1), …, K(x, xn)]IC+ΩELM-1L(4)

式(4)中, (x1, x2, …, xn)为给定训练样本, n为样本数量, K为核函数。 本工作选择径向基函数作为核函数, 其表达式为

K(xi, xj)=exp-12xi-xj‖2·s-2(5)

根据ELM的理论, 输入权值、 偏置值和隐含层节点数通常是随机设置的。 因此, 输入矩阵与隐层矩阵之间的关系通常是一种随机映射。 而在KELM训练过程中, 将随机映射替换为核映射, 提高了模型的鲁棒性。 其中正则化系数C和核参数s是KELM网络的重要参数, 需要对其进行优化。

1.2 麻雀搜索算法

麻雀搜索算法(sparrow search algorithm, SSA)[21]是根据麻雀觅食并逃避捕食者的行为而提出的群智能优化算法, 是一种通过模拟自然现象的进化算法。 麻雀搜索算法主要模拟了麻雀觅食的过程, 为了完成觅食, 麻雀个体通常被分为探索者和追随者, 由找到食物较好的个体作为探索者, 其他个体作为追随者, 同时在种群中选择一定比例的个体进行侦查预警, 会对周围环境保持警惕以防天敌的到来, 如果发现危险则放弃食物, 以确保安全。

每个麻雀个体有属性和行为两个信息。 每个个体只有一个属性, 即所在的位置信息, 表示该个体找到食物的位置。 个体所拥有的行为分为三类: (1) 作为探索者, 继续搜索食物; (2) 作为追随者, 跟随一个发现者觅食。 (3) 警戒侦查, 遇到天敌发生危险则放弃食物。

若在D维空间中, 每只麻雀个体的位置为P=(x1, x1, …, xD), 适应度值为fi=f(X), 麻雀种群总数为N, 其中Ne只个体作为探索者, 剩余N-Ne只为追随者。 探索者作为寻找食物的个体, 需要最先更新在空间中的位置, 式(6)为探索者位置的更新过程的迭代形式

xi, dt+1=xi, dtexp((-i)(αitermax)-1), λSTxi, dt+Q, λ≥ST(6)

式(6)中, xi, dt为第t代中第i个个体在空间中第d维的位置, α 为随机数, 范围(0, 1], Q为标准正态分布随机数, λ 为[0, 1]中的均匀随机数, ST为警戒阈值, 取值范围为[0.5, 1.0]。 当λ 大于ST时, 该发现者将按正态分布随机移动到当前位置附近。

追随者更新位置的过程如式(7),

xi, dt+1=Qexp(xwi, dt-xbi, dt), in2xbi, dt+1D∑d=1D(rand{-1, 1}(|xbi, dt-xi, dt|)), i≤n2(7)

式(7)中, xw和xb分别为当前种群中麻雀最差的位置和最优的位置, 该过程为在当前最优位置附近随机找一个位置, 且每一维距最优位置的方差将会变得更小, 即不会出现在某一维上与最优位置相差较大, 而其他位置相差较小。

在麻雀觅食的同时会有部分个体负责警戒, 当遇到危险时, 无论该麻雀是探索者还是追随者, 都将放弃当前的食物而移动到一个新的位置。 每代将从种群中随机选择S个个体进行预警行为。 其位置更新公式如式(8)

xi, dt+1=xbi, dt+β(xi, dt-xbi, dt), fi≠fbxi, dt+kxi, dt-xwi, dt|fi-fw|+δ, fi=fb(8)

式(8)中, β 为标准正态分布的随机数, k为[-1, 1]之间的均匀随机数, δ 是一个防止分母为1的很小的数, fw为最差位置的麻雀适应度, fb为当前最优位置的适应度。

1.3 SSA-KELM

通过麻雀搜索算法与KELM相结合, 避免了人工进行参数寻优的复杂过程, 不仅节省了大量调参时间, 还能够保证模型参数的有效性和预测结果的准确性, 使得模型拥有更加强的泛化性能。

SSA-KELM建模流程如图1所示, 将测试集误差作为SSA算法的适应度函数, 利用麻雀搜索算法对KELM模型中的正则化系数和核参数进行优化求解。 对以上两个参数进行全局寻优, 优化得到各元素定标模型中的正则化系数和核参数。 利用训练集训练最终得到各元素的SSA-KELM模型。

图1 SSA-KELM模型建模流程Fig.1 Modeling process of SSA-KELM

2 实验部分
2.1 试验系统

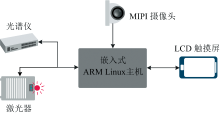
采用自主研发的LIBS废钢成分测试系统, 其结构如图2所示。 实验设备基于瑞芯微RK3399 pro、 Lapa-80激光器(脉冲能量80 mJ可调、 频率0~20 Hz可调), AvaSpec-Mini4096CL小型光纤光谱仪2台(波长范围: 170~300 nm, 290~400 nm), 高精度光路探头, 非同轴光路和光纤激光通过光纤聚焦到样品表面2 mm的距离, 以保证检测精度。 整个光谱采集与预处理过程在基于C++的嵌入式高精度分析系统中完成, 该系统集成光谱数据采集控制、 光谱仪多通道数据融合、 光谱数据筛选与背景杂散光过滤、 人机交互控制数据库存储等功能, 实现光谱数据预处理与分析预测一体化。

图2 实验系统结构Fig.2 Experimental system structure

2.2 样品

为了提升模型定标精度, 参考火花直读光谱定标模型中低合金钢样品范围, 选用试验样品均为国家标准样品, 成分见表1。 其中编号1#— 6#为中低合金YSBS23207-97系列的A1至A6号样品; 编号7#— 12#为低合金钢GSB-03-2615系列的1至6号样品, 每个样品在实验前均保持表面洁净。

表1 钢铁样品中的元素含量(wt%) Table 1 Element components of steel samples (wt%)
2.3 方法

为确保便携式LIBS废钢成分检测仪能提供稳定的光谱信号, 需要在实验过程中进行最佳实验条件及参数的调试与设置, 结合现有相关LIBS定量分析研究, 对激光器参数进行多次调试优化与实验对比以及对系统中采集与处理设备进行适配调试后, 最终将激光器的实验参数设定为电压130 V, 脉冲频率2 Hz, 积分时间1.05 ms, 延迟时间1.28 μ s。 为降低实验波动影响, 每个试验样品表面均匀选取28个不同检测位置, 每个位置处激发50个脉冲, 前10次激发的脉冲用于祛除样品表面污渍, 第11— 50次为有效数据。 由于样品在成分与结构上的多样性, 可能导致不同位置的元素分布的差异。 同时, 在激光诱导击穿的过程中, 能量逐渐在样品中传播耗散, 也会使得部分元素的激发受到限制, 进而造成光谱信号的弱化。 而且, 样品中的基体成分也可能引入误差。 为了处理实验过程可能出现的异常值及误差, 需要对每个位置获取的光谱数据进行光谱预处理。 首先将每个光谱数据进行合并拼接, 其次通过利用K值校验方法(K=2.5), 剔除可能产生粗大误差的异常数据, 并将剩余数据进行平均处理, 以改善由激光器波动造成的光谱数据不稳定影响, 进而提高定量分析的准确性与可靠性。 最终每个样品得到28个平均光谱数据, 12个样品共336组数据。 为了验证模型的预测性能, 将YSBS23207-97和GSB-03-2615两个系列的第4号样品, 即4#和10#样品作为测试集用于对Si、 Cr、 C、 Mn、 Ni、 Cu、 Ti、 V、 Al元素模型进行测试, 其余10组样品作为校正集用于模型的训练与验证。

3 结果与讨论
3.1 光谱预处理

3.1.1 基线校正处理

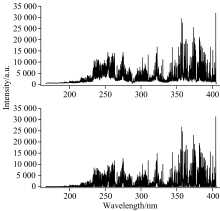
在等离子光谱生成过程中, 等离子体受到多种内部因素的影响, 如黑体辐射、 韧致辐射和复合辐射等, 同时, 激光器能量的不可避免的波动、 样品表面不均匀和透镜与样品的距离等一些外部因素也会产生影响, 导致光谱产生连续背景, 并使光谱的基线发生波动, 这些波动会对数据的稳定性产生影响, 不利于实验的稳定进行。 为了使实验效果更加准确, 首先对获得的光谱进行基线校正处理, 使基线保持稳定, 采用了文献[22]中的基线校正方法, 获取全谱所有极小值点集合, 首先计算全部极小值点的平均值与相对标准差的比值, 将此比值乘以一定的因子用以修正极小值筛选的阈值。 其次, 计算当前极小值点与后一个极小值点的方差比, 通过比较相邻两个极小值点的方差比与筛选阈值来剔除不合理的极小值, 最后使用线性差值法扩大极小值估计点, 同时使用多项式函数进行拟合, 得到估计背景并进行校正。 图3为基线校正前后的光谱数据图对比, 可以看出基线在处理后变得更加平稳。

图3 光谱数据基线校正前后对比Fig.3 Comparison of spectral data before and after baseline correction

3.1.2 特征谱线筛选

因元素的含量与其所对应的波长的谱线强度具有相关性, 所以筛选出待测元素的各个特征谱线的波长作为输入特征。 此外, 由于废钢内多种元素之间相互作用和影响, 元素含量与谱线强度之间并非完全呈线性关系。 为了更准确的模拟实际情况, 需要选择基体元素的多条特征谱线, 以引入一定程度的非线性关系。 我们参考美国国家标准与技术研究院(NIST)谱线数据库, 结合获得的光谱数据, 选择明显的峰值谱线作为最终确定的特征谱线。 表2列出了经过筛选的谱线, 选取了Al、 C、 Si等9种待测元素与基体元素铁(Fe)的特征谱线共66条, 用于后续处理。

表2 实验所用各元素及对应的特征谱线 Table 2 Characteristic lines of elements used in the experiment

与其他光谱技术一样, 激光诱导击穿光谱技术容易受到信号波动的影响。 得到的光谱在各个波长上的强度值分布范围相差较大。 如果不进行任何处理, 分析结果容易产生较大差异。 因此, 需要对特征谱线进行处理。 在建立定量分析模型之前, 对筛选得到的谱线进行归一化处理, 以确保定量模型的稳定性。 在LIBS研究中, 常用内标法作为校正与标定方法, 即将与分析元素相关的发射线的峰强度除以与内标元素相关的选定发射线的谱线强度, 以进行样品的定量测量。 内标法的主要目的是消除样品之间的成分差异和仪器响应的变化, 从而提高定量分析的准确性, 内标法的效果与所选用与被测元素的内标谱线的接近程度相关, 选择越接近的谱线效果越好。 根据在分析线附近选择内标线的概念与表2中元素谱线的分布情况, 我们选择Fe 354.10 nm谱线归一化其余65谱线, Fe 354.10 nm不作为模型的输入。 将归一化后的65条谱线作为模型输入, 用来建立V、 Ti、 Al模型。 同样, 选择Fe 271.44 nm谱线归一化其余65谱线, 使用归一化后的谱线作为输入建立Si、 Cr、 C、 Mn、 Ni、 Cu元素模型。

3.2 单变量内标法模型

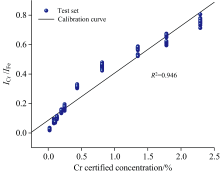
使用铁元素271.44 nm谱线作为内标法的标准谱线, 建立了包含9种元素的内标法准校正模型。 图4展示了Cr的校准曲线, 决定系数表明浓度与相对强度之间存在强烈的关系。 该模型展示了元素浓度与强度之间的良好线性关系, 尤其是在低元素浓度中几乎不受基体效应和自吸收的影响。 然而, 随着元素浓度的增加, 基体效应和自吸收变得更加强烈, 出现非线性关系。 使用单变量建模各元素的评估指标列在表3中, 很明显, 单变量模型分析结果的不确定性波动较明显。

图4 Cr元素校准曲线Fig.4 Cr calibration curve

表3 内标法各元素模型的评估指标结果 Table 3 Evaluation indicators of models for each element using internal standard method
3.3 SSA-KELM模型训练与验证

使用经过预处理后的65条谱线作为KELM模型的输入, 将建模元素的含量作为模型的输出。 按4∶ 1随机划分谱线为训练集和验证集分别用于模型的训练与验证。 KELM模型中的正则化系数C和核参数s是决定模型稳健性的重要参数; 手动调整参数不仅困难耗时, 而且容易陷入局部最优解。 为了解决这一问题, 将SSA算法与KELM结合进行参数寻优, 找到最优解, 利用SSA算法更加快速高效, 模型泛化能力更好。

将预测集的误差被用作SSA算法的适应度函数, 用于对KELM模型中的两个参数C和s进行全局搜索。 训练集用于训练KELM模型。 根据实验结果, SSA方法将样本大小设置为200, 最大迭代次数设置为500, 警告值设置为0.8, 参数搜索优化设置为1到1 000。 经过对9个元素的模型进行寻优后, 均得到了最优的核参数和正则化系数。 精确模型参数搜索的结果显示在表4中。

表4 麻雀搜索算法寻优后的各元素模型参数 Table 4 Model parameters of each element after sparrow search algorithm optimization

为了判断模型的训练效果, 以相关决定系数(R2)、 验证均方根误差(RMSEC)和测试均方根误差(RMSEP)作为评估指标对模型进行测试。 评估指标的计算公式如式(9)和式(10)

R2=1-∑i=1n(c^i-ci)2∑i=1n(ci-c-)2(9)

$\text { RMSE }=\sqrt{\frac{\sum_{i=1}^{n}\left(c_{i}-\hat{c}_{i}\right)^{2}}{n}}$(10)

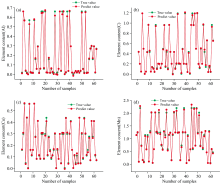
式(9)和式(10)中, n为样本数, ci为元素真实的浓度, c^i为对应的元素预测浓度, c-为个样本中所有浓度值的平均值。 验证集RMSE指标为RMSEC; 测试集的则为RMSEP。

图5为部分元素模型验证集的含量预测值与实际值偏差情况, 表5为各元素模型在评估指标下的结果。 从图5和表5可以得出, SSA算法优化后的KELM模型的预测能力较好, 利用SSA-KELM得到的V元素的R2在0.98以上, 其他元素的R2均在0.99以上, 呈现出良好的拟合性能, 具有较高的准确性。 验证集和测试集的RMSE也较为出色, 相比于单变量校正模型, 预测能力有明显的提升。 使用多变量模型能够利用其优秀的非线性拟合能力进一步减弱各元素之间的影响、 基体效应波动和自吸收效应所产生的无法表示的非线性误差, 对多种元素谱线建立的模型能够显示出良好的非线性关系, 且效果较好, 同时也证明了SSA-KELM模型应用在便携式LIBS废钢检测的可行性。

图5 部分元素模型验证集的预测结果Fig.5 The prediction results of some element models on the validation set

表5 各元素模型的评估指标结果 Table 5 Evaluation indicators for each element model

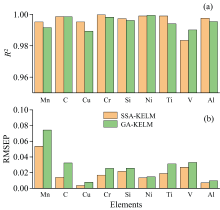
为了验证SSA-KELM的预测能力, 还采用了遗传算法(GA)优化的KELM模型进行对比, 设定相同的实验条件, 并设置算法参数: 种群数量为200, 最大迭代次数为500, 交叉变异概率为0.7和0.1, 以轮盘赌进行选择。 针对多种元素建立GA-KELM校正模型。 比较SSA-KELM和GA-KELM两种模型的R2、 RMSEP、 建模速度, 如图6所示。 在平均建模速度上, SSS-KELM为32.6 s, GA-KELM为47.1 s。 可以得出, 麻雀搜索算法的快速收敛性, 使得SSA-KELM模型建模速度更快。 同时, 麻雀搜索算法不易陷入局部最优解, 与KELM的结合使得模型更能够准确表现基体效应和自吸收效应所产生的非线性关系, 尽管这种非线性关系在实际应用中很难被明确描述。

图6 各元素模型的R2 (a)和RMSEP (b)对比Fig.6 Comparison of each element model on (a) R2 and (b) RMSEP

4 结论

LIBS技术与多变量校正法结合已经成为各行业为消除自吸收效应和基体效应而广泛使用的方式。 为提高钢企中废钢利用效率, 快速检测废钢中元素含量, 引入了一种新方法SSA-KELM结合便携式LIBS技术。 实验提取了各检测元素和基体元素的多条特征谱线进行建模测试, 并利用麻雀搜索算法对网络参数进行高效寻优, 得到了良好的定量模型。 同时针对待测元素建立了单变量校正模型和GA-KELM校正模型, 对比显示, 利用SSA-KELM结合便携式LIBS能够有效针对谱线的非线性关系进行良好的拟合, 弱化自吸收效应和基体效应, 且建模速度更快, 效果更优。 建模结果显示C、 Mn、 Cu、 Si、 Ni、 Ti、 V、 Al元素模型验证集的相关决定系数分别为0.995 2、 0.998 6、 0.995 2、 0.999 7、 0.997 3、 0.999、 0.999、 0.983 4、 0.997 6, 测试集的RESEP分别为0.213、 0.014、 0.003、 0.016、 0.021、 0.013、 0.018、 0.026、 0.007。 表明, SSA-KELM模型与便携式LIBS相结合能够为钢铁企业提供一种便携的快速检测方法, 用于废钢回收过程中的现场实时分析, 有效提高废钢利用效率。

参考文献
[1] Xuan Y, Yue Q. Resources, Conservation and Recycling, 2017, 120: 186. [本文引用:1]
[2] Dworak S, Fellner J. Resources, Conservation and Recycling, 2021, 173: 105692. [本文引用:1]
[3] Schroeder W W, Van Niekerk J J, Dicks L, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 1971, 26(6): 331. [本文引用:1]
[4] Prosr P, Polansky R, Pihera J. Proceedings of 2013 IEEE International Conference on Solid Dielectrics (ICSD), 2013: 740. [本文引用:1]
[5] Pereira G R, Rocha H S, Anjos M J, et al. Proceedings of 2006 IEEE Nuclear Science Symposium Conference Record, 2006, 6: 3932. [本文引用:1]
[6] Díaz D, Hahn D W, Molina A. Spectrochimica Acta Part B: Atomic Spectroscopy, 2017, 136: 106. [本文引用:1]
[7] Li X, Yang S, Fan R, et al. Optics & Laser Technology, 2018, 102: 233. [本文引用:1]
[8] Kim Y, Fabre C, Cauzid J. Spectrochimica Acta Part B: Atomic Spectroscopy, 2022, doi: 10.1016/j.sab.2022/106397. [本文引用:1]
[9] Bhatt C R, Goueguel C L, Jain J C, et al. Applied Optics, 2017, 56(28): 7789. [本文引用:1]
[10] Court A. Raman-LIBS, a Journey From Mars to Earth Via the Moon. 2019 IEEE Aerospace Conference, 2019, 1, doi: 10.1109/AERO.2019.8741619. [本文引用:1]
[11] Ruan F, Qi J, Yan C, et al. Journal of Analytical Atomic Spectrometry, 2017, 32(11): 2194. [本文引用:1]
[12] Sezer B, Unuvar A, Boyaci I H, et al. Journal of Cereal Science, 2022, 104: 103435. [本文引用:1]
[13] Afgan M S, Hou Z, Wang Z. Journal of Analytical Atomic Spectrometry, 2017, 32(10): 1905. [本文引用:1]
[14] Sheng L, Zhang T, Wang K, et al. Chemical Research in Chinese Universities, 2015, 31(1): 107. [本文引用:1]
[15] Zhu C, Lv J, Liu K, et al. Microchemical Journal, 2021, 168: 106408. [本文引用:1]
[16] Rifai K, Özcan L, Doucet F, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2020, 165: 105766. [本文引用:1]
[17] GUO Zhi-wei, SUN Lan-xiang, ZHANG Peng, et al(郭志卫, 孙兰香, 张鹏, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(1): 278. [本文引用:1]
[18] Mei Y G, Cheng S S, Hao Z Q, et al. Plasma Science and Technology, 2019, 21(3): 171. [本文引用:1]
[19] Huang G B, Zhu Q Y, Siew C K. Neurocomputing, 2006, 70(1-3): 489. [本文引用:1]
[20] Huang G B, Ding X, Zhou H. Neurocomputing, 2010, 74(1-3): 155. [本文引用:1]
[21] Xue J, Shen B. Systems Science & Control Engineering, 2020, 8(1): 22. [本文引用:1]
[22] Sun L, Yu H. Spectrochimica Acta Part B: Atomic Spectroscopy, 2009, 64(3): 278. [本文引用:1]