Kubelka-Munk(KM)模型由Kubelka和Munk于1931年提出^[17], 适用于半透明或者不透明介质。 KM模型假设光线在传到介质表面时大部分被完全散射, 小部分在介质中继续传播, 且这两种运动方向都垂直于界面。 假设介质厚度无限大, KM模型的公式可简化为

f(R∞)=(1-R∞)22R∞=KS(1)

式(1)中, R_∞ 为光谱反射率, f(R_∞ )为吸收散射比, K和S分别为吸收系数和散射系数。

根据KM理论, 吸收系数和散射系数适用于加和性原理。 混合物中的每个成分都有唯一确定的吸收系数和散射系数, 彼此独立, 互不影响。

颜料识别采用计算未知颜料K/S曲线与标准颜料K/S曲线的相似度实现。 常用的匹配算法包括基于波形特征的匹配、 基于光谱编码的匹配和基于统计指标的匹配。 本文结合颜料K/S曲线光谱角余弦算法与归一化欧氏距离算法, 对未知颜料K/S曲线进行识别。

1.2.1 相似度计算方法

(1) 光谱角余弦

光谱角余弦计算两条曲线的相似性, 是将K/S曲线看作是n维空间的向量, 两个向量的广义夹角越小, 光谱角余弦越接近1, 说明越相似。 对于具有n个波段的K/S曲线x=(x₁, x₂, …, x_n)和y=(y₁, y₂, …, y_n), 光谱角余弦定义为

$SAC\left( x, y \right)=\frac{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\,{{x}_{i}}{{y}_{i}}}{\sqrt{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\,x_{i}^{2}}\sqrt{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\,y_{i}^{2}}}$(2)

式(2)中, x_i和y_i分别为未知K/S曲线和标准K/S曲线在第i波段的数值, n为K/S曲线波段数, 光谱角余弦越接近1, 两条曲线的形状越相似。

(2) 归一化欧氏距离

归一化欧氏距离是从幅度计算曲线的相似性, 主要描述了K/S曲线之间幅值的差异。 归一化欧氏距离越小, K/S曲线之间相似度越大, 对于具有n个波段的K/S曲线x=(x₁, x₂, …, x_n)和y=(y₁, y₂, …, y_n), 归一化欧氏距离的数学定义为

$Ed\left( x, y \right)=\sqrt{\frac{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\,{{({{x}_{i}}-{{y}_{i}})}^{2}}}{n}}$(3)

1.2.2 光谱角余弦与归一化欧氏距离结合

将光谱角余弦进行翻转, (1-SAC)与归一化欧氏距离有相同的取值范围, 经过实验验证, 对光谱角余弦和归一化欧氏距离分别赋以0.6和0.4的权重识别效果最好, 光谱角余弦-归一化欧氏距离计算相似度的公式可表示为

dSAC, Ed(x, y)=(1-SAC(x, y))×0.6+Ed(x, y)×0.4(4)

式(4)中, d_{SAC, Ed}(x, y)的取值范围为[0, 1], 匹配原则为“ 值越小, 光谱曲线越相似” 。

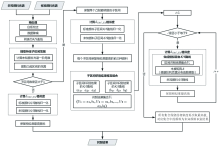
基于KM理论的光谱分段识别方法, 根据未知颜料光谱一阶导数曲线的“ 凸起” 提取未知颜料K/S曲线的子区间; 采用式(4), 计算子区间范围内未知颜料与标准颜料K/S曲线的相似度; 子区间识别结果相互组合, 结合丰度矩阵生成模拟混合K/S曲线, 计算与未知颜料K/S曲线的相似度得到最终识别结果, 具体步骤如下:

(1) 获取未知颜料与标准颜料的光谱数据并进行预处理, 运用式(1), 将未知颜料光谱与标准颜料光谱转换为K/S曲线;

(2) 对未知颜料光谱进行一阶导数计算, 导数曲线具有明显“ 凸起” 的部分, 视作特征子区间的光谱范围, 按照该范围提取出未知颜料K/S曲线的特征子区间, 用于后续的分段识别;

(3) 若子区间数等于1, 则认为未知颜料为纯净颜料, 在全波段范围内运用d_{SAC, Ed}(x, y)计算未知颜料与标准颜料K/S曲线的相似度, 相似度最高的标准颜料视为识别结果, 跳转到第7); 否则, 则保留两个“ 凸起” 最明显的子区间, 在子区间范围内, 对未知颜料与标准颜料的K/S曲线进行最大最小值归一化计算, 并运用d_{SAC, Ed}(x, y)计算未知颜料与标准颜料K/S曲线在区间范围内的相似度, 每个子区间的识别结果保留相似度最高的前三种颜料;

(4) 从区间Ⅰ 保留的识别结果(Result_Ⅰ ={a₁, a₂, a₃}), 和子区间Ⅱ 保留的识别结果(Result_Ⅱ ={b₁, b₂, b₃})中依次取出一种颜料的K/S曲线, 两两组合成包含9个元素的识别结果集合(U₁={a₁, b₁}, U₂={a₁, b₂}, …, U9={a₃, b₃});

(5) 根据狄利克雷分布函数得到2× 1 000维的丰度矩阵A, 与区间识别结果集合中的2条标准颜料K/S曲线生成1 000条不同丰度混合而成的模拟混合K/S曲线, 再次运用d_{SAC, Ed}(x, y)计算未知颜料K/S曲线与1 000条模拟混合K/S曲线的相似度, 保留相似度最高值。

(6) 对区间识别结果集合中的9个组合元素均进行步骤(5)的运算, 在保留的9个相似度中再次取最高值, 对应集合中的标准颜料为混合颜料的组成成分。

(7) 给出颜料识别结果。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 颜料识别流程图Fig.1 Pigment identification flow chart

从颜料标准样本库中选用壁画中常见的石青、 石绿、 石黄和朱砂, 制作纯净颜料样本, 再将四种纯净颜料按50∶ 50的质量比两两混合, 制作六组混合颜料样本。 按照如下步骤制作样本: 取出适量明矾颗粒, 用冷水浸泡, 明矾颗粒膨胀透明后缓慢加入少量沸水, 用玻璃棒搅拌至明胶完全溶解; 将颜料粉末放入调色碟中, 用滴管将胶液少量多次滴入到调色碟, 同时用手指研磨搅拌, 直至胶液与颜料粉末混合均匀; 最后用笔刷蘸满颜料, 在宣纸上绘制4 cm× 4 cm的正方形。 图2和图3分别为制作的4组纯净颜料样本和6组混合颜料样本, 使用实验室构建的标准颜料光谱库对制作的颜料样本进行分析。 光谱库中的标准颜料来源于姜思序堂、 天雅、 金源阳光三个品牌, 通过文献查阅、 颜料分析专家咨询, 首批选用了壁画中常见的矿物颜料96种、 植物颜料6种、 合成颜料13种与樱花牌墨汁1种, 为了解粒径的不同对于光谱的影响, 矿物颜料中包含7种不同粗细程度的石青和石绿颜料, 以及3种不同粗细程度的朱砂颜料。 对选择的116种颜料均用刷子进行1次、 2次、 3次绘制, 分别得到三种不同厚度的颜料样本, 作为颜料识别的参考样本。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 纯净颜料样本 (a): 石青; (b): 石绿; (c): 石黄; (d): 朱砂Fig.2 Pure pigment samples (a): Azurite; (b): Malachite; (c): Orpiment; (d): Cinnabar

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 混合颜料样本 (a): 50%石青+50%石绿; (b): 50%石青+50%石黄; (c): 50%石青+50%朱砂; (d): 50%石绿+50%石黄; (e): 50%石绿+50%朱砂; (f): 50%石黄+50%朱砂Fig.3 Mixed pigment samples (a): 50%Azurite+50%Malachite; (b): 50%Azurite+50%Orpiment; (c): 50%Azurite+50%Cinoabar; (d): 50%Malachite+50%Orpiment; (e): 50%Malachite+50%Cinnabar; (f): 50%Orpiment+50%Cinnabar

采用美国Themis Vision System公司的VNIR400H型高光谱成像仪, 单景画幅大小为1 392像元× 1 000像元, 光谱分辨率为2.8 nm, 可覆盖400~1 000 nm波长的光谱范围, 包含了可见光与近红外一共1 040个波段。 对样本进行成像数据采集, 进行白板校正及降噪预处理后, 提取出4组纯净样本和6组混合样本的光谱曲线, 如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 颜料样本光谱曲线 (a): 纯净颜料样本光谱曲线; (b): 混合颜料样本光谱曲线Fig.4 Pigment samples spectra (a): Spectra of pure pigment samples; (b): Spectra of mixed pigment samples

2.3.1 一阶导数

特征波段选择采用一阶导数方法, 可以去除部分噪声对目标光谱的影响, 并有助于突出光谱曲线在某波长处细微的变化。 若λ 为波长, R为反射率, 一阶导数可用式(5)表示为

$R\left( {{\lambda }_{i}} \right)'=\frac{\text{d}R}{\text{d}\lambda }=\frac{\ \ \ \ {{R}_{{{\lambda }_{i+1}}}}\ \ \ -\ \ \ {{R}_{{{\lambda }_{i}}}}\ \ \ \ }{ \Delta \lambda }$(5)

2.3.2 最大最小值归一化

最大最小值归一化是将每个点减去所在变量列的最小值后, 除以所在变量列最大值与最小值的差。 很多情况下, 由于外界光照强度的不同, 同种物质的K/S曲线存在尺度上的变化。 因此, 对数据进行最大值最小值归一化可以减小数据尺度差异过大带来的影响, 如式(6)

${{R}_{N}}=\frac{R\ \ \ -\ \ \ {{R}_{\text{min}}}}{\ \ \ \ \ \ {{R}_{\text{max}}}\ \ \ -\ \ \ {{R}_{\text{min}}}\ \ \ \ \ }$ (6)

式(6)中, R为原始数据, R_min为数据最小值, R_max为数据最大值, R_N为最大最小值归一化的数据, 取值范围为[0, 1]。

一般用于壁画分析的成像光谱仪的光谱范围都在可见近红外波段, 波长大约为400~1 000 nm, 以石黄和朱砂的混合光谱为例, 混合颜料的反射率光谱和一阶导数曲线如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 石黄朱砂混合光谱曲线与一阶导数曲线 (a): 混合光谱: 50%石黄和50%朱砂; (b): 一阶导数曲线: 50%石黄和50%朱砂Fig.5 Reflectance spectral and 1st curve of Orpiment and Cinnabar (a): Mixed spectra: 50%Orpiment and 50% Cinnabar; (b): 1st curve: 50%Orpiment and 50% Cinnabar

从图5可以看出, 在混合颜料的一阶导数曲线上, 有两个明显的“ 凸起” , 即430~560和561~865 nm区域, 表征着石黄与朱砂的混合光谱在相应波段范围反射率明显上升, 之后保持大概稳定或缓慢上升。 在后续分区间的识别计算中, 根据未知颜料光谱一阶导数曲线的“ 凸起” 确定出各个子区间的范围。 六组混合颜料的特征子区间如表1所示。

表1

Table 1

表1(Table 1)

表1 混合颜料样本特征子区间 Table 1 Mixed pigment samples characteristics interval 混合颜料 子区间1/nm 子区间2/nm 石青石绿 400~525 790~985 石青石黄 440~605 800~1 000 石青朱砂 400~515 516~660 石绿石黄 430~700 745~1 000 石绿朱砂 400~575 576~650 石黄朱砂 430~560 561~865

表1 混合颜料样本特征子区间 Table 1 Mixed pigment samples characteristics interval

在400~1 000 nm范围内, 六组混合样本都可提取出两个子区间, 在子区间范围内, 对混合颜料和标准颜料的K/S曲线用式(6)进行最大最小值归一化处理, 再按式(4)对处理后的光谱进行相似度计算, 六组混合颜料的区间识别结果如表2所示, 其中加粗颜料是与混合颜料真值一致的识别结果。

表2

Table 2

表2(Table 2)

表2 混合颜料样本的区间识别结果 Table 2 Interval identification results of mixed pigment samples 混合颜料 子区间1识别结果 子区间2识别结果 石青石绿 石青、 绿玛瑙、 白方解 石绿、 头青、 银粉 石青石黄 珍品石黄、 雌黄、 珍珠粉 石绿、 石青、 二绿 石青朱砂 石青、 头青、 石青粉 胭脂膏、 朱砂、 胭脂 石绿石黄 珍品石黄、 雌黄、 雌黄粉 二绿、 头绿、 珍品石绿 石绿朱砂 石绿、 蛤粉、 水晶末 朱砂、 红珊瑚、 胭脂膏 石黄朱砂 雌黄、 石黄、 雌黄粉 漂净朱砂、 朱砂、 朱砂粉

表2 混合颜料样本的区间识别结果 Table 2 Interval identification results of mixed pigment samples

通过将子区间的识别结果与已知真值对比分析, 可知每个子区间的识别结果均至少包含一个真值, 证明子区间可以有效提取出混合颜料中纯净颜料的特征。

根据Bioucas-Dias方法等的^[18], 利用区间识别结果集合与丰度矩阵, 由线性光谱模型得到模拟混合K/S曲线。 区间识别结果集合U的大小为2n, 其中n为波段数; 丰度矩阵A的大小为2× 1 000, 由狄利克雷分布函数得到。 以石黄和朱砂的混合样本为例, 根据每个区间保留的三种识别结果, 可以得到九个区间识别结果集合。 按式(4)对每个子集生成的1 000条混合数据与混合颜料的K/S曲线进行识别计算, 相似度取最大值。 石黄和朱砂混合样本九个区间识别结果集合保留的最大相似度如表3所示。

表3

Table 3

表3(Table 3)

表3 石黄朱砂混合颜料样本识别结果集合保留的相似度 Table 3 Similarity of retention of endmember subsets of Orpiment and Cinnabar mixed pigment samples 识别结果 漂净朱砂 朱砂 朱砂粉 雌黄 0.957 2 0.958 6 0.953 8 石黄 0.965 1 0.969 5 0.958 2 雌黄粉 0.966 9 0.965 1 0.954 4

表3 石黄朱砂混合颜料样本识别结果集合保留的相似度 Table 3 Similarity of retention of endmember subsets of Orpiment and Cinnabar mixed pigment samples

通过对表3的分析可知, 在所有保留的相似度中, 包含石黄和朱砂的区间识别结果集合的相似度最高, 说明石黄和朱砂是混合样本组分颜料的可能性最大。 六组混合样本的识别结果如表4所示。

表4

Table 4

表4(Table 4)

表4 混合颜料样本的最终识别结果 Table 4 Final identification results of mixed pigment samples 混合颜料 识别结果 石青石绿 石青、 石绿 石青石黄 石青、 珍品石黄 石青朱砂 石青粉、 朱砂 石绿石黄 头绿、 珍品石黄 石绿朱砂 石绿、 红珊瑚 石黄朱砂 石黄、 朱砂

表4 混合颜料样本的最终识别结果 Table 4 Final identification results of mixed pigment samples

通过分析六组混合样本的识别结果可以发现, 除石绿朱砂混合样本, 其余五组混合样本均识别正确。

为了验证提出方法的有效性, 对包含混合颜料与纯净颜料的模拟壁画进行颜料识别。 识别点位分布如图6, 识别结果如表5, 将各个点位的识别结果与模拟壁画各个区域的真值对比, 除橙色区域3中的朱砂颜料外, 全部识别正确。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 模拟壁画中进行颜料识别的位置Fig.6 Simulating the location of pigment identification in a mural

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 混合颜料未知光谱与模拟光谱对比 (a): 模拟光谱: 雌黄和真银珠; (b): 模拟光谱: 漂净朱砂和石青Fig.7 Comparison of mixed pigments unknown spectra and simulated spectra (a): Simulated spectra: Orpiment1 and Vermilion; (b): Simulated spectra: Cinnabar1 and Azurite

表5

Table 5

表5(Table 5)

表5 模拟壁画颜料识别结果 Table 5 Identification results of pigment in a mural 点号 识别结果 真值 1 花青 花青 2 石绿 石绿 3 雌黄、 真银朱 雌黄粉、 朱砂 4 石青、 漂净朱砂 石青、 朱砂 5 石青、 漂净朱砂 石青、 朱砂

表5 模拟壁画颜料识别结果 Table 5 Identification results of pigment in a mural