引用本文
张秀全, 马世兴, 李志伟, 郑德聪, 宋海燕. 褐土全氮含量Vis/NIRS组合预测模型的构建[J]. 光谱学与光谱分析, 2024,44(8): 2310-2317.
ZHANG Xiu-quan, MA Shi-xing, LI Zhi-wei, ZHENG De-cong, SONG Hai-yan. Prediction of Total Nitrogen Content in Brown Soil Based on Hyperspectral and Combined Prediction Model[J]. Spectroscopy and Spectral Analysis, 2024,44(8): 2310-2317.
Doi:10.3964/j.issn.1000-0593(2024)08-2310-08  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
褐土全氮含量Vis/NIRS组合预测模型的构建
张秀全1, 马世兴1, 李志伟2,*, 郑德聪1, 宋海燕1
1.山西农业大学农业工程学院, 山西 太谷 030801
2.山西农业大学信息科学与工程学院, 山西 太谷 030801
*通讯作者 e-mail: lizhiweitong@163.com

作者简介: 张秀全, 1980年生, 山西农业大学农业工程学院讲师 e-mail: zhangxiuq1980@126.com

收稿日期: 2023-04-17 修回日期: 2023-09-21
基金: 国家重点研发计划子课题(2021YFD1600301-4), 中央引导地方科技发展资金项目(YDZJSX20231C009), 校学术恢复项目(2023XSHF2)资助
摘要

准确掌握农田土壤全氮含量对于评估土壤肥力, 合理施用氮肥具有重要意义。 为综合利用各个单预测模型的优势, 提升整体预测性能、 降低模型方差, 提高鲁棒性, 以农田褐土土壤为研究对象, 基于近红外-可见光高光谱数据, 提出了一种基于标准差的预测有效度组合预测模型(CPM), 用于预测土壤全氮含量。 对原高光谱数据采用Savitzky-Golay平滑和一阶微分变换, 采用树模型进行特征波段提取, 利用决策树回归(DTR)(模型1)、 高斯核回归(GKR)(模型2)、 随机森林回归(RF)(模型3)、 LASSO回归(模型4)、 多层感知器回归(MLP)(模型5)5个单预测模型, 通过单预测模型的线性组合建立组合预测模型。 结果表明: (1)通过广义简约梯度优化算法求得组合预测模型中5个单预测模型的权重分别为ω1*=0.407,ω2*=0.378,ω3*=0.215,ω4*=0,ω5*=0; (2)对于所有数据, 基于5种单预测模型和组合预测模型对土壤全氮含量预测的预测有效度分别为 M1=0.855, M2=0.856, M3=0.847, M4=0.785, M5=0.796, MCPM=0.880; 与单模型预测有效度最大值相比, 组合预测模型预测有效度提高了2.924%; (3)对于所有数据, 基于5种单预测模型和组合预测模型对土壤全氮含量预测的预测精度和标准差分别为 E( A1)=0.924, σ( A1)=0.075, E( A2)=0.928, σ( A2)=0.077, E( A3)=0.923, σ( A3)=0.082, E( A4)=0.882, σ( A4)=0.109, E( A5)=0.889, σ( A5)=0.104, E( ACPM)=0.937, σ( ACPM)=0.066, 与单模型预测精度最大值相比, 组合预测模型预测精度提高了0.970%, 模型稳定性提高了12.000%, 且为优性组合预测。 组合预测模型可用于可见光-近红外光谱数据的农田褐土土壤全氮含量的有效估测, 可为农田土壤全氮含量的快速监测提供依据和参考。

关键词: 可见光-近红外; 高光谱预测; 全氮含量; 组合预测模型
中图分类号:S153.621 文献标志码:A
Prediction of Total Nitrogen Content in Brown Soil Based on Hyperspectral and Combined Prediction Model
ZHANG Xiu-quan1, MA Shi-xing1, LI Zhi-wei2,*, ZHENG De-cong1, SONG Hai-yan1
1. College of Agricultural Engineering, Shanxi Agricultural University, Taigu 030801, China
2. College of Information Science and Engineering, Shanxi Agricultural University, Taigu 030801, China
*Corresponding author
Abstract

Accurately grasping the total nitrogen content of farmland soil is significant for evaluating soil fertility and applying nitrogen fertilizer reasonably. To comprehensively utilize the advantages of each single prediction Model, improve the overall prediction performance, reduce the variance of the model, and improve the robustness, this study takes farmland brown soil as the research object, and based on near-infrared and visible hyperspectral data, puts forward a Combined prediction model based on standard deviation. CPM was used to predict soil total nitrogen content. Savitzky-Golay smoothing and first-order differential transformation are applied to the original hyperspectral data, and a tree model is used for feature band extraction. Using five single prediction models, Decision Tree Regression (DTR) (Model 1), Gaussian Kernel Regression (GKR) (Model 2), Random Forest Regression (RF) (Model 3), LASSO Regression (Model 4), and Multi-Layer Perceptron (MLP) (Model 5), a combination prediction model is established through a linear combination of single prediction models. The results indicate that: (1) The weights of the five single prediction models in the combined prediction model are obtained by generalized reduced gradient optimization algorithm:ω1*=0.407,ω2*=0.378,ω3*=0.215,ω4*=0,ω5*=0; (2) For all data, the predictive effectiveness of five single prediction models and combined prediction models for predicting soil total nitrogen content is M, respectively M1=0.855, M2=0.856, M3=0.847, M4=0.785, M5=0.796, MCPM=0.880, compared to the maximum predictive validity of a single model, the predictive validity of the combination prediction model has increased by 2.924%; (3) For all data, the prediction accuracy and standard deviation of soil total nitrogen content based on five single prediction models and combined prediction models are E( A1)=0.924, σ( A1)=0.075, E( A2)=0.928, σ( A2)=0.077, E( A3)=0.923, σ( A3)=0.082, E( A4)=0.882, σ( A4)=0.109, E( A5)=0.889, σ( A5)=0.104, E( ACPM)=0.937, σ( ACPM)=0.066, compared to the maximum prediction accuracy of a single model, the combination prediction model has improved prediction accuracy by 0.970% and model stability by 12.000%, making it an optimal combination prediction model. The combined prediction model can effectively estimate the total nitrogen content of farmland brown soil based on visible-near-infrared spectral data and can provide a basis and reference for the rapid monitoring of the total nitrogen content of farmland soil.

Keyword: Visible-near infrared; Hyperspectral estimation; Total nitrogen content; Combination prediction model
引言

氮素是作物生长的重要营养元素之一, 低氮不利于作物的生长, 但过度施氮也会损害作物生长, 破坏生态环境。 因此, 快速、 高效监测土壤氮含量对评价土壤肥力和合理施氮至关重要[1]。 传统的土壤氮含量测定具有破坏性、 耗时耗力、 实效差、 代表性不足, 较难满足实际生产的需求[2, 3]。 可见光-近红外光谱技术因其快速、 非破坏性和成本效益高等特点, 在土壤养分含量估算中已得到广泛应用[4, 5, 6]。

近年来, 针对土壤氮含量的可见光-近红外光谱预测进行了大量研究, 并逐渐探索组合预测模型以提高预测精度和稳健性。 目前的研究主要集中在利用各种光谱数据处理技术和统计方法, 结合特征提取技术与机器学习或深度学习模型, 以充分利用高光谱数据中的信息来提高预测精度。 例如, 结合S-G平滑、 各阶微分、 倒数微分、 散射校正、 小波分析等光谱数据处理与主成分分析(PCA)、 偏最小二乘回归(PLSR)、 竞争性自适应加权算法(CARS)、 连续投影算法(SPA)、 无信息变量消除(UVE)、 随机森林特征选择算法(RFFS)等方法提取的特征与支持向量机(SVM)、 随机森林(Random Forest)、 极限学习机(ELM)、 反向传播神经网络(BPNN)、 梯度提升决策树(GBDT)和极端梯度提升(XGBoost)等机器学习算法和卷积神经网络(CNN)等深度学习算法, 构建组合预测模型从而提高土壤氮含量的预测性能[5, 6, 7, 8, 9, 10, 11, 12, 13, 14]。 陈昊宇等[9]基于分数阶微分结合支持向量机和BP神经网络模型建立了土壤全氮反演模型, 结果表明利用1.1阶微分处理与BP神经网络模型精度最佳; 杨梅花等[10]对可见光-近红外土壤光谱采用PCA、 UVE和UVE-SPA三种变量特征选择方法建立了PLSR、 LS-SVM、 BPNN和遗传算法优化的反向传播神经网络(GA-BPNN)土壤全氮含量预测模型, 结果显示, 结合UVE-SPA的特征选择和LS-SVM模型估算土壤全氮含量表现较好。 Shi等[11]对土壤光谱反射率进行一阶和二阶导数变换, 并利用逐步多元回归(SMLR)、 PLSR和SVMR估算土壤总氮含量, 发现PLSR和SVMR方法获得了相似的估计精度, 并且都优于SMLR方法, 且光谱的一阶导数比二阶导数得到了更准确的结果。 Wang等[12]比较了四种光谱预处理方法(基线校正、 平滑、 降维和特征选择)结合3种传统的机器学习方法(PLSR、 RF、 ELM)构建的土壤总氮预测模型, 结果表明基线校正和平滑的ELM模型效果较好, 并对3种传统机器学习与深度学习方法(CNN)比较, 发现具有卷积神经网络(CNN)结构的深度学习模型显示出比传统机器学习方法更高的准确性。

已有研究多采用单一的机器学习或深度学习模型来构建土壤氮含量预测模型。 为减少单一模型可能存在的偏差, 获得更为准确和稳定的预测结果, 研究者们探索了基于Bagging、 Boosting、 stacking等集成学习方法构建的预测模型和基于加权方法构建的融合模型, 通过整合不同模型的优势, 实现更准确的预测效果。 例如, 张秀全等[15]利用4种单预测模型构建的堆叠泛化模型在预测土壤有机质含量中表现出较好的精度。 集成学习模型虽然利用了多个单一模型在结构和预测上的差异程度, 但未考虑多个模型在集成堆叠模型中的贡献程度。 关于模型加权融合在土壤氮含量预测方面的研究较少。 且已有研究中土壤氮含量预测精度多以决定系数和误差作为评价标准[6, 7, 8, 9, 10, 11, 12, 13, 14, 15], 组合模型的精度评价以误差平方和、 误差绝对值之和为目标函数, 考虑误差的分布情况较少。 因此, 本研究提出了一种组合预测模型, 该组合预测模型建立在多个单项预测模型的基础上, 构建考虑预测精度标准差的预测有效度的组合模型并以构建的预测有效度模型最大作为目标, 采用规划求解思想求得各单预测模型的权重, 以此权重进行加权构建组合预测模型。 该组合预测模型综合利用了各单项预测模型的信息, 可以更加有效地提高预测精度, 以期为农田土壤表层全氮含量的高光谱快速定量估算提供方法、 为科学决策分析提供依据。

1 实验部分
1.1 土壤样本采集与处理

在2021年10月初, 作物收割之后, 选定太谷区内、 大豆玉米种植试验农田作为采样区, 土壤类型均为褐土, 按照规划的路线, 在每个采样单元的相对中心位置, 按照等量、 随机以及五点混合的原则采集土壤样本, 以确保所获取的土壤数据兼具精确性和代表性, 共采集246个土壤样本。 为减小土壤水分含量对光谱的影响, 经过手工清理杂物并自然风干后, 所有土壤样本被分为两份, 一份经过研磨并过筛, 以便进行土壤全氮含量的精确测定; 另一份则用于高光谱图像的采集, 以捕捉样本的详细光谱特性。

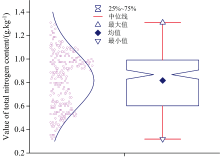
土壤全氮含量测定采用蒸馏后滴定法。 土壤全氮含量的统计结果如图1所示, 246个样本的全氮含量最小值达到0.319 g· kg-1, 最大值为1.311 g· kg-1, 反映了土壤氮含量的丰富变化。 平均值为0.818 g· kg-1, 反映了整体氮含量的中等水平。 中位数为0.868 g· kg-1, 进一步强调了大多数样本氮含量的集中趋势。 此外, 标准差为0.138 g· kg-1, 显示出氮含量分布的离散程度。 变异系数为29.112%, 揭示了氮含量在不同样本间的相对变化率。

图1 土壤全氮含量统计Fig.1 Statistics of total nitrogen content in soil samples

1.2 土壤光谱数据测定及预处理

在室内采用美国Headwall Photonics公司的Starter Kit扫描平台对246个土壤样本进行了近红外-可见光高光谱反射率的测定。 光谱范围为379.663~1 704.28 nm, 共计1 029个波段。 其中, 可见光光谱的分辨率为0.727 nm, 而近红外光谱的分辨率则为4.715 nm, 物距精确设置为20 nm, 并将移动速度控制在15.55 mm· s-1, 曝光时间设定为0.9 ms。

将扫描得到的可见光-近红外高光谱图像导入ENVI5.3软件进行处理。 在ENVI5.3中, 利用感兴趣区域(region of interest, ROI)工具选取土壤样本区域并输出样本区域的光谱反射率平均值, 以此作为该土壤样本的光谱反射率数值。 为了减少光谱测定的误差, 提升反射率数据与土壤全氮含量之间的相关性, 原始光谱进行Savitzky-Golay去噪[图2(a)]、 对去噪光谱数据进行一阶微分光谱变换[图2(b)]。

图2 土壤光谱反射率及一阶微分变换光谱反射率曲线Fig.2 Original spectra (a) and the first derivative spectra of soil samples

由图2(a)可知, 土壤样本反射率在0.07~0.27之间, 各样本的光谱曲线波动形态相似, 光谱反射率均随着波长的增加逐渐增加, 且到1 000 nm处反射率趋于稳定, 在400~880 nm波段内的反射率增加幅度较大, 1 000~1 700 nm反射率变化幅度减缓。 在近红外波段, 受土壤成分有机质、 矿物质等的影响对光的吸收较小, 因此近红外区的反射率较可见光波段高。 由图2(b)可知, 经过一阶微分变换之后的光谱曲线的差异特征更加突出。

1.3 模型构建

1.3.1 决策树回归模型

决策树回归模型(decision tree regressor, DTR)[16]通过递归地将输入空间划分为两个子区域来构建二叉决策树。 为了构建这棵树, 模型通过求解函数$\underset{j, s}{\mathop{\text{min}}}\,[\underset{{{c}_{1}}}{\mathop{\text{min}}}\,\underset{{{x}_{i}}\in {{R}_{1}}\left( j, s \right)}{\mathop \sum }\,{{({{y}_{i}}-{{c}_{1}})}^{2}}+(\underset{{{c}_{2}}}{\mathop{\text{min}}}\,\underset{{{x}_{i}}\in {{R}_{2}}\left( j, s \right)}{\mathop \sum }\,\left( {{y}_{i}}-{{c}_{2}}{{)}^{2}} \right)$, 选择最优切分变量j与切分点s, 并决定相应的输出值。

1.3.2 高斯核回归模型

高斯核回归模型(Gaussian kernel regression, GKR)[17]是一种通过核函数捕捉数据的非线性结构。 在给定训练数据集和新的输入点x* 的情况下, y* 是基于所欲训练数据点的加权平均。 即${{y}_{\text{*}}}=\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,{{w}_{i}}k\left( {{x}_{\text{*}}},{{x}_{i}} \right)$, 其中 kx* , xi=exp-x-x* ‖22σ2, wi是权重。

1.3.3 随机森林模型

随机森林(random forest, RF)[17]是一种集成学习算法, 通过自助采样方法(bootstrap sampling)生成多个独立的决策树模型。 RF的核心目标函数定义为: Cα (Tt)=C(Tt)+α |Tt|, 其中, α 为正则化参数, 用于平衡模型的复杂度与拟合度; |Tt|是子树T的叶子节点数量, 反映了模型的复杂度; C(Tt)为预测误差, 采用最小均方差(mean squared error, MSE)来度量, 体现了模型的拟合程度。

1.3.4 LASSO回归模型

LASSO回归模型(least absolute shrinkage and selection operator, LASSO)[18]在损失函数中引入了L1正则化项, 损失函数为Q(β )=‖ y-Xβ ‖ 2+λ ‖ β ‖ 1, 式中, y是观测值; λ 为控制惩罚程度的调整参数模型参数; β 为参数向量。

1.3.5 MLP模型

MLP即多层感知器(multi-layer perceptron)[19], 它的输入是x, 输出y是hw, b(x), 通过调整其权重w和偏置b拟合已有训练数据(x, y)所反映出来的输入输出关系。 其目标函数为hw, b(x)=f(wx+b), 其中f(· )为激活函数。

1.3.6 CPM模型

组合预测模型(combination prediction model, CPM)采用单预测模型的线性组合构建, 其原理为[式(1)]

ft=ω1f1t+ω2f2t+ω3f3t+ω4f4t+ω5f5t(1)

式(1)中, ft为组合预测模型预测值; f1t、 f2t、 f3t、 f4t和f5t分别为DTR、 GKR、 RF、 LASSO和MLP模型的第t个样本的预测值(t=1, 2, 3, …, 246); ω 1, ω 2, ω 3, ω 4, ω 5分别为DTR、 GKR、 RF、 LASSO和MLP模型的权重系数, 权重系数之和为1。

组合预测模型构建过程如图3所示。

图3 组合预测模型构建过程Fig.3 Construction process of combination prediction model

1.4 模型精度验证

1.4.1 单模型预测精度验证

单模型预测精度采用预测有效度进行评价, 预测有效度计算方法[20]为[式(2)— 式(6)]

Mi=E(Ai)[1-σ(Ai)](2)

式(2)中

$\text{E}\left( {{A}_{i}} \right)=\frac{1}{n}\overset{n}{\mathop{\underset{t=1}{\mathop \sum }\,}}\,{{A}_{it}}$(3)

$\sigma \left( {{A}_{i}} \right)={{\left[ \frac{1}{n}\overset{n}{\mathop{\underset{t=1}{\mathop \sum }\,}}\,{{({{A}_{it}}-E({{A}_{i}}))}^{2}} \right]}^{\frac{1}{2}}}$ (4)

Ait=1-|eit|当|eit|≤10当|eit|≥1(5)

eit=xt-xitxti=1, 2, 3, …, 5; t=1, 2, 3, …, n; n=246(6)

式(3)— 式(6)中, Mi为第i种预测方法的预测有效度, 值越大表示第i种预测方法越有效; E(Ai)为第i种单预测方法的预测精度序列的数学期望, 值越大精度越高; σ (Ai)为第i种预测方法的预测精度序列的标准差, 值越小模型越稳定; t为预测样本数; xt为t个样本的实测值; xit为第i种预测方法第t个样本的预测值; Ait为第i种预测方法在第t个样本的预测精度, 当Ait=0表示第i种预测方法在第t个样本的预测为无效预测。

1.4.2 组合预测模型精度验证

组合预测模型采用预测有效度进行验证, 预测有效度计算方法[20]为[式(7)]

M=E(A)[1-σ(A)](7)

式(7)中, E(A)为组合预测方法的预测精度序列的数学期望, σ (A)为组合预测方法的预测精度序列的标准差, 且E(A)和σ (A)均为单项预测方法加权系数ω 1, ω 2, …, ω 5的函数, 记为M(ω 1, ω 2, …, ω 5), 组合预测模型M的计算方法[17]为[式(8)]

$\begin{align} & \text{maxM}\left( {{\omega }_{1}},{{\omega }_{2}},\ldots ,{{\omega }_{5}} \right)=\frac{1}{n}\overset{n}{\mathop{\underset{t=1}{\mathop \sum }\,}}\,\left[ 1-\left| \overset{5}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,{{\omega }_{i}}{{e}_{it}} \right| \right]\cdot \\ & \left\{ 1-{{\left[ \frac{1}{n}\overset{n}{\mathop{\underset{t=1}{\mathop \sum }\,}}\,{{\left( 1-\left| \overset{5}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,{{\omega }_{i}}{{e}_{it}} \right| \right)}^{2}}-\frac{1}{{{n}^{2}}}{{\left( \overset{n}{\mathop{\underset{t=1}{\mathop \sum }\,}}\,\left( 1-\left| \overset{5}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,{{\omega }_{i}}{{e}_{it}} \right| \right) \right)}^{2}} \right]}^{\frac{1}{2}}} \right\} \\ \end{align}$(8)

式(8)中, t为预测样本数(n=246), i为单预测模型个数, 记Mmin和Mmax分别为5种预测方法的最小和最大预测有效度, M为组合模型的预测有效度, 则有: M< Mmin时, 组合预测模型为劣性组合预测; Mmin< M< Mmax时, 组合预测模型为非劣性组合预测; M> Mmax时, 组合预测模型为优性组合预测。

1.5 广义简约梯度算法

组合预测模型的最优解基于非线性广义简约梯度法(generalized reduced gradient)求得[21]。 优化问题可简化为[式(9)]

minF(X)X∈Ens.t.H(X)=0L≤x≤UL, U∈En(9)

式(9)中, H(x)=[h1(X), h2(X), …, hm(X)]T, L=[l1, l2, …, ln]T, U=[u1, u2, …, un]T。

在求解过程中, 将X的全部向量分解为两部分, 一部分是基向量, 其维度为m; 另一部分是非基向量, 维度为n-m, 即X=[XB, XN]T。 相应地, L=[LB, LN]T, U=[UB, UN]T。

由隐函数存在定理可知, 存在一个连续映射XB=V(XN), 使得原始的n个变量的目标函数转化为低维的n-m个变量的函数f(XN), 该f(XN)在Xk关于XN的梯度即为简约梯度, f(XN)关于XN的简约梯度可表示为∇f( XNk)=∇NF(Xk)-∇N H(Xk)[∇BH(Xk)]-1-∇BF(X2)。

简记简约梯度为∇f( XNk)=[r1, r2, …, rn-m]T, 定义Sk=[s1, s2, …, sn-m]T, 其中, 当 xm+jk=lm+j且rj> 0时, 或当 xm+jk=um+j且rj< 0时 sjk=0, 其余情形 sjk=-rj。 使得 XNk+1= XNk+α Sk, 然后令Y0= XBk, 用下式进行迭代: Yc+1=Yc-[∇BH(Y0 XNk+1)]-1H(Yc, XNk+1), c=1, 2, …, 最后求得满足H(Yc+1, XNk+1)=0的Yc+1, 即可得到优化的值。

2 结果与讨论
2.1 特征波段选取

通过随机森林特征重要度算法实现特征波段的筛选。 在随机森林中, 每棵决策树的每个节点都基于某个特征的条件来判断, 以将数据集按照不同的响应变量划分为两个子集。 为了选择最优的条件, 使用不纯度(impurity)作为模型衡量标准。 在训练决策树时, 计算每个特征对于减少树的不纯度的贡献。 当构建整个随机森林时, 计算每个特征在所有树中平均减少的不纯度, 该平均值作为特征选择的依据, 从而确定各特征的重要性。

特征个数设置了从5到100, 以5为步长, 共20个梯度, 以验证集的决定系数R2和均方误差MSE作为精度验证分析特征个数的最佳选择, 结果如图4所示。 随着特征个数的增加验证集的决定系数R2和均方误差MSE均呈波动趋势, 在特征个数为40时表现出决定系数R2较大, 同时均方根误差MSE较小, 因此选择40个特征波段作为后续的模型构建, 特征重要性估算值结果如图5所示。 筛选出的40个特征波段重要性介于0.21~0.47之间, 特征波段中近红外区域波段数占到75%, 主要分布于1 000~1 100 nm, 1 400和1 600 nm附近, 可见光区域波段数占到25%, 主要分布于510~600 nm、 820 nm附近, 与已有研究结果基本一致[22, 23]。

图4 不同特征波段个数精度验证Fig.4 Accuracy verification of the number of different feature bands

图5 波段重要性衡量Fig.5 Band importance measurement

2.2 模型预测精度

将一阶微分光谱数据集按7∶ 2∶ 1的比例划分为训练集、 验证集和测试集3部分, 以选择的40个波段光谱数据为自变量, 土壤全氮含量为因变量, 运用决策树回归(decision tree regressor, DTR)(模型1)、 高斯核回归(Gaussian kernel regression, GKR)(模型2)、 随机森林回归(random forest regression, RF)(模型3)、 LASSO回归(模型4)、 多层感知器回归(multi-layer perceptron, MLP)(模型5)5个单预测模型分别构建土壤全氮含量预测模型。 使用预测精度数学期望E(A)、 标准差σ (A)和预测有效度M(A)作为精度评价指标, 其中E(A)和M(A)值越大模型拟合程度越好; σ (A)值越小模型越稳定。 预测精度结果如表1所示。

表1 模型预测精度对比分析 Table 1 Comparison of estimation accuracies

基于5种单预测模型的预测结果计算各单预测模型的预测精度序列的数学期望E(Ai)、 标准差σ (Ai)及相关系数ρ ij, 基于组合预测最优化模型[式(8)]中得到组合模型预测有效度最大的目标函数maxM(ω 1, ω 2, …, ω 5)模型, 利用非线性目标规划求解原理进行求解, 对于训练集: ω1* =0.538, ω2* =0.377, ω3* =0.085, ω4* =0, ω5* =0, M( ω1* , ω2* , …, ω5* )=0.916; 对于验证集: ω1* =0.369, ω2* =0.343, ω3* =0.261, ω4* =0, ω5* =0, M( ω1* , ω2* , …, ω5* )=0.816; 对于测试集: ω1* =0.291, ω2* =0.351, ω3* =0.358, ω4* =0, ω5* =0, M( ω1* , ω2* , …, ω5* )=0.852; 对于所有数据: ω1* =0.407, ω2* =0.378, ω3* =0.215, ω4* =0, ω5* =0, M( ω1* , ω2* , …, ω5* )=0.880, 组合预测模型预测有效度提高了2.924%。 对于训练集、 验证集、 测试集和全部数据的单预测模型和组合预测模型均表现为组合预测的有效度M(A)大于单预测模型的最大有效度M(A), 均表现为优性预测模型。 在训练集、 验证集、 预测集和所有数据集上, 组合模型的预测精度E(A)和标准差σ (A)均优于5种单模型。

从单预测模型的预测精度(表1)的结果可以看出, 对于同一组数据集, 不同的预测方法在预测集、 验证集和训练集上的预测精度表现出不一致的现象, 可能会出现欠拟合和过拟合的现象, 为此, 有必要发挥各个单预测模型的优势, 创新性地构建单模型的组合模型。 在利用高光谱技术对土壤全氮含量进行预测时, 评估预测精度的常见指标主要有决定系数(R2)、 平均绝对误差(MAE)和均方根误差(RMSE)等[7, 8, 9, 10, 11, 12], 此类评价指标主要考虑各样本的误差大小, 对于组合模型的评价指标主要有误差平方和、 误差绝对值之和, 均未考虑误差的分布情况。 在已有研究中对于组合预测模型中各单项预测模型的权重系数多通过简单平均法、 误差倒数法为原则进行确定[24, 25], 会带来组合预测模型有可能未达到最优解, 对于所有数据通过算术平均法计算组合权重系数, ω1* =0.207, ω2* =0.207, ω3* =0.205, ω4* =0.190, ω5* =0.191, M( ω1* , ω2* , …, ω5* )=0.855, 组合预测模型有效度0.855不显著大于单预测模型预测有效度的最大值0.856, 预测精度E为0.924小于单模型中的预测精度的最大值0.928, 预测标准差为σ 为0.074小于单模型中的预测标准差的最小值0.075, 该组合模型为非劣性模型; 通过误差倒数法构建的组合预测模型中 ω1* =0.231, ω2* =0.261, ω3* =0.261, ω4* =0.119, ω5* =0.128, M( ω1* , ω2* , …, ω5* )=0.831, 组合预测模型有效度0.831不显著大于单预测模型预测有效度的最大值0.856, 预测精度E为0.921小于单模型中的预测精度的最大值0.928, 预测标准差σ 为0.097大于单模型中的预测标准差的最小值0.075, 该组合模型为非劣性模型; 本研究组合模型中LASSO、 MLP两个单预测模型的权重系数为0, 表明这2个单项预测模型是冗余预测方法, 相比简单平均法和误差倒数法获得的组合预测模型, 提高组合预测模型精度, 且该组合预测模型至少是非劣性预测, 当任意两种单预测模型的预测精度序列的相关系数ρ ij∈ (-1, 1)时, 该组合预测方法是优性组合预测方法, 相关系数ρ ij∈ (-1, 1)此条件一般来说是很容易满足的, 因此该组合预测模型较大程度上利用了各单预测模型提供的信息。 本研究只针对预测模型的组合方式在土壤全氮含量预测中进行了初步分析, 选择的单项预测模型的个数较有限, 对光谱数据的处理也仅采用了一阶微分, 特征提取也仅采用了随机森林特征重要度算法, 下一步可以引入不同分数阶微分处理技术[26]和多种特征提取[10, 13, 23], 选择更多的单预测模型进行对比, 以建立一个更全面、 更合适的组合预测模型, 来提高土壤全氮预测的准确性和泛化性。

进一步对建立的5种模型的土壤全氮真实值与预测值的拟合程度进行分析, 通过决定系数R2对拟合程度进行评价(图6)。 从图6可以看出, 5个模型的拟合决定系数R2分别为0.892、 0.904、 0.907、 0.786、 0.801, 组合预测模型的拟合决定系数R2达到了0.933, 较5种单模型中决定系数最高的0.907提高了2.867%。

图6 各模型土壤全氮实测值与预测值的拟合分布Fig.6 Fitting distribution of measured and predicted soil total nitrogen values for each model

2.3 残差分析

为了进一步对构建的模型进行合理性和可靠性诊断, 分析了各模型的残差分布, 结果如图7所示, 5个单模型和组合模型的残差均表现为随机分布, 不含趋势信息且不存在异方差特征, 表明构建的6个模型均合理, 且组合模型的残差值小于5个单模型。

图7 各模型残差分布图Fig.7 The residual distribution of each model

3 结论

以典型农田褐土土壤样本为研究对象, 对土壤表层全氮的可见光-近红外高光谱特征进行分析, 采用DTR、 GKR、 RF、 LASSO、 MLP 5种单预测模型和基于5种单预测模型的加权线性组合构建的最优组合预测模型, 对土壤全氮含量进行了预测; 分析了5种单预测模型和组合预测模型在土壤全氮含量预测精度的差异性。 主要结论如下:

(1)通过目标规划求解构建的最优组合预测模型中DTR、 GKR、 RF、 LASSO、 MLP单预测模型的加权系数分别为 ω1* =0.407, ω2* =0.378, ω3* =0.215, ω4* =0, ω5* =0; 最优化组合模型中LASSO、 MLP单预测模型方法只提供冗余信息, 且CPM组合模型为优性组合模型。

(2)组合模型预测有效度M(A)为0.880, 较单模型预测有效度M(A)最大值提高了2.924%; 组合模型的稳定性σ (A)为0.066, 较单模型稳定性σ (A)最小值提高了12.000%。 相较于单预测模型, 组合模型在土壤全氮含量的高光谱预测方面展现出了显著的优势。 这一模型不仅提升了预测精度, 还拓宽了机器学习模型在土壤全氮含量预测领域的应用范围。

参考文献
[1] Liu Jun, Cai Haotian, Chen Shan, et al. Agriculture, 2023, 13(4): 743. [本文引用:1]
[2] ZHOU Yang, ZHAO Xiao-min, GUO Xi(周洋, 赵小敏, 郭熙). Acta Pedologica Sinica(土壤学报), 2022, 59(2): 451. [本文引用:1]
[3] Bai Zijin, Xie Modong, Hu Bifeng, et al. Sensors, 2022, 22(16): 6124. [本文引用:1]
[4] ZHANG Yao, CUI Yun-tian, DENG Qiu-zhuo, et al(张瑶, 崔云天, 邓秋卓, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2021, 52(S1): 310. [本文引用:1]
[5] CHEN Wei, XU Zhan-jun, GUO Qi(陈玮, 徐占军, 郭琦). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2022, 38(8): 9. [本文引用:2]
[6] Zhang Xianglin, Xue Jie, Xiao Yi, et al. Remote Sensing, 2023, 15(2): 465. [本文引用:3]
[7] Lin Lixin, Liu Xixi. Computer and Electronics in Agriculture, 2022, 192(0): 106634. [本文引用:3]
[8] ZHANG Xin, YANG Chao, LIU Hong-bin, et al(张鑫, 杨超, 刘洪斌, 等). Tobacco Science & Technology(烟草科技), 2022, 55(8): 20. [本文引用:3]
[9] CHEN Hao-yu, XIANG Lei, GAO He, et al(陈昊宇, 项磊, 高贺, 等). Remote Sensing for Natural Resources(自然资源遥感), 2023, 35(3): 170. [本文引用:4]
[10] YANG Mei-hua, ZHAO Xiao-min, FANG Qian, et al(杨梅花, 赵晓敏, 方倩, 等). Scientia Agricultura Sinica(中国农业科学), 2014, 47(12): 2374. [本文引用:5]
[11] Shi T, Cui L, Wang J, et al. Plant and Soil, 2013, 366: 313. [本文引用:4]
[12] Wang Y, Li M, Ji R, et al. Sensors, 2020, 20(24): 7078. [本文引用:4]
[13] Ma J J, Cheng J, Wang J H, et al. Information Processing in Agriculture, 2022, 9: 566. [本文引用:3]
[14] ZHANG Heng, LIANG Tai-bo, FENG Wen-qiang, et al(张恒, 梁太波, 冯文强, 等). Chinese Tobacco Science(中国烟草科学), 2023, 44(5): 103. [本文引用:2]
[15] ZHANG Xiu-quan, LI ZHi-wei, ZHENG De-cong, et al(张秀全, 李志伟, 郑德聪, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(3): 903. [本文引用:2]
[16] ZHOU Zhi-hua(周志华). Maching Learning(机器学习). Beijing: Tsinghua University Press(北京: 清华大学出版社), 2016. [本文引用:1]
[17] DONG Xue-mei, WANG Jie-wei(董雪梅, 王洁微). Pattern Recognition and Artificial Intelligence(模式识别与人工智能), 2019, 32(7): 589. [本文引用:3]
[18] WANG Lu, SUN Ju-bo(王璐, 孙聚波). Journal of Jilin Engineering Normal University(吉林工程技术师范学院学报), 2021, 37(12): 109. [本文引用:1]
[19] WANG Qiang, HU Rong(王强, 胡荣). Computer Engineering and Design(计算机工程与设计), 2022, 43(12): 3443. [本文引用:1]
[20] CHEN Hua-you, HOU Ding-pi(陈华友, 侯定丕). Journal of Systems Engineering(系统工程学报), 2003, 18(3): 203. [本文引用:2]
[21] MA Wei-biao, WANG Hong-yan, RUI Qiang(马伟标, 王红岩, 芮强). Journal of System Simulation(系统仿真学报), 2012, 24(4): 774. [本文引用:1]
[22] Stenberg B, Viscarra Rossel R A, Mouazen A M. Advances in Agronomy, 2010, 107: 163. [本文引用:1]
[23] WANG Wen-cai, ZHAO Liu, LI Shao-wen, et al(王文才, 赵刘, 李绍稳, 等). Acta Agricultruae Zhejiangensis(浙江农业学报), 2018, 30(9): 1576. [本文引用:2]
[24] Wang Y, Liao Z, Stéphanie Mathieu, et al. Journal of Hazardous Materials, 2021, 404(Pt A): 123965. [本文引用:1]
[25] ZHANG Peng-cheng, LI Wei-juan, WANG Jun(张朋程, 李伟娟, 王军). China Energy and Environmental Protection(能源与环保), 2023, 45(6): 198. [本文引用:1]
[26] Hong Y, Liu Y, Chen Y, et al. Geoderma, 2019, 337: 758. [本文引用:1]