基于W几何形的恒星光谱分子带检测

引用本文

陈奋, 王颖, 刘福窑. 基于W几何形的恒星光谱分子带检测[J]. 光谱学与光谱分析, 2024,44(8): 2279-2283.
CHEN Fen, WANG Ying, LIU Fu-yao. Spectral Molecular Band Detection Based on W Geometry[J]. Spectroscopy and Spectral Analysis, 2024,44(8): 2279-2283.
Doi:10.3964/j.issn.1000-0593(2024)08-2279-05 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于W几何形的恒星光谱分子带检测

陈奋^1,², 王颖^1,^2,^*, 刘福窑^1,²

1.上海工程技术大学数理与统计学院, 上海 201620

2.上海工程技术大学计算物理与应用研究中心, 上海 201620

*通讯作者 e-mail: wangying424524@163.com

作者简介: 陈奋, 女, 1998年生, 上海工程技术大学数理与统计学院硕士研究生 e-mail: chenfen199812@163.com

收稿日期: 2023-04-13 修回日期: 2023-10-20

基金: 国家自然科学基金青年科学基金项目(11803020)和国家自然科学基金项目天文联合基金项目(U2031145)资助

摘要

研究关注由分子内部能级变化引起的光谱分子带的识别和检测, 有助于研究恒星光谱类型和参数估计。首先从分子带的曲线趋势出发, 运用曲线分析对分子带进行识别, 并剔除具备W形但下降趋势明显的伪分子带。借鉴多类型多分类准则的识别思路, 将检测出的分子带尖峰深度、 W形宽度、曲线趋势和回升趋势四个参数作为训练特征。这四个参数综合考虑了始点变化速率、曲线变化趋势、极值点分布和曲线形状因素。其次, 为了验证该方法的可行性与可靠性, 利用LightGBM (light gradient boosting machine)模型分别对F型恒星光谱和分子带特征参数进行识别, 准确率分别为97.62%和99.16%, 进一步验证了所提取分子带的准确性。本工作不仅能挖掘出晚期恒星, 提高数据标签的准确性, 还能在准确识别的基础上, 利用LightGBM机器学习模型检测未知型光谱自动识别晚期恒星, 提高了识别效率并且减少了内存占用。

关键词: W几何形特征; 分子带检测; 曲线趋势; 分类识别; 恒星光谱

中图分类号:P144.1 文献标志码:A

Spectral Molecular Band Detection Based on W Geometry

CHEN Fen^1,², WANG Ying^1,^2,^*, LIU Fu-yao^1,²

1. School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai 201620, China

2. Center of Application and Research of Computational Physics, Shanghai University of Engineering Science, Shanghai 201620, China

*Corresponding author

Abstract

This study focuses on identifying and detecting spectral molecular bands caused by changes in internal energy levels of molecules, which contributes to the research of stellar spectral types and parameter estimation. First, considering the curve trend of molecular bands, pseudo molecular bands that have a W shape but an obvious downward trend should be eliminated by using curve analysis to identify molecular bands. Bringing the identification idea of multi-type and multi-classification criteriainto the model, the four parameters of the detected molecular band peak depth, W-shaped width, curve trend, and rebound trend are adoptedas training features, which consider comprehensivelythe change rate of starting point, change trend of curve, extreme point distribution and the factors of curve shape. Secondly, the LightGBM (Light Gradient Boosting Machine) model is used to identify the spectral and molecular band characteristic parameters of F-type stars with an accuracy of 97.62% and 99.16%, respectively, to verify the feasibility and reliability of this method. This work can not only excavate the late stars and improve the accuracy of data labels but also automatically identify the late stars by using the LightGBM machine learning model to detect the unknown spectrum based on accurate recognition, which improves recognition efficiency and reduces memory occupation.

Keyword: W geometry feature; Molecular band detection; Curve trend; Classification recognition; Spectral classification

文章图片

引言

自大型巡天项目(如LAMOST郭守敬望远镜、 SDSS斯隆数字巡天和GAIA盖亚卫星等)开展以来, 所收集到的恒星光谱已达千万量级^[1]。恒星光谱是恒星的“ 身份” 象征, 它蕴含了有效温度、重力加速度和金属丰度等信息。黄轶琦等^[2]基于已知恒星参数信息的光谱通量数据, 构建纯数据驱动的The Cannon机器学习方法对恒星参数进行测量。 Paunzen等^[3]对汞锰星(CP3)进行证认时利用到了MKCLASS标准光谱库和LAMOST DR4中的光谱数据。挖掘恒星光谱信息不仅对恒星参数进行估计, 还能提高恒星识别和分类的准确性。恒星的光谱是由连续谱及在连续谱中的许多吸收线或发射线组成^[4]。恒星光谱的吸收峰特征客观反映了该恒星的组成元素。而组成元素相同的恒星, 其光谱强度取决于恒星大气层的有效温度和压强。在这一背景下, Gray^[5]研究得到F型恒星在特定的有效温度下, 恒星大气中的某些化学元素可以形成双原子分子, 并能够持续存在, 从而导致分子带的出现, 特别是G波段的CH分子带, 这使得分子带成为了检验晚于F3型恒星的重要判别指标之一。文献[6, 7, 8, 9]运用Lick线指数计算光谱特征, 但不能对光谱次型进行精确分类。

在探索恒星化学丰度和温度时, 吸收峰的提取直观反映了结果的准确性。而分子带是由多个吸收峰组成的带状吸收峰。其形状类似于W形, 两边高, 中间低的结构。中晚期恒星带状吸收峰的存在增加了光谱特征提取和恒星光谱分类的难度。本文旨在辨别真分子带和伪分子带, 提出了基于W形特点的分子带检测。通过该方法可以检测出光谱中是否含有真分子带, 从而能够快速识别出中晚期恒星, 提高恒星分类的准确性。

1 W几何形

设X_i[us, ve]为第i条光谱在波长us与波长ve之间的通量, 记为X_i=(x_i(us), x_i(us+1), …, x_i(ve)), i=0, 1, …, N, us为波段中的起始波长, ve为波段中的截止波长, N为光谱数量, 为避免混淆, 本文中令

$x_{i} (us) = x_{ius}$ (1)

1.1 形状因子

形状因子用来度量波段中是否含有类W形, 初步判断是否含有明显的分子带。在几何图形中, W是由两个V(V₁, V₂)组成, 设ν ₁₁、 ν ₁₀、 ν ₁₂分别为第1个V的左顶点、尖峰点和右顶点所对应的波长, $x_{ν_{11}}$ 、 $x_{ν_{10}}$ 、 $x_{ν_{12}}$ 为其各波长所对应的通量。类W形状因子的判断准则s₁为

$s_{1} = \{\begin{array}{l} 0, & ν_{12} \neq ν_{21} \\ 1, & ν_{12} = ν_{21} \end{array}$ (2)

若初步判断准则s₁=1, 则进一步根据准则s₂确定其是否构成带状, s₂公式为

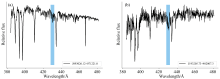
$s_{2} = \{\begin{array}{l} 0, & 其他 \\ 1, & (x_{ν_{11}} > x_{ν_{21}}) 且 (x_{ν_{21}} < x_{ν_{22}}) \end{array}$ (3)

为防止出现伪W形的错误判断[见图1, (a)中粗体黑色曲线为W形, 但整体框架中下降趋势明显, 为伪W形; (b)为真分子带], 对符合以下条件的V形进行整合, 整合后再计算准则s₁和s₂, 具体如下:

	Figure Option View Download New Window
	图1 形状因子中V形整合示例图 (a)和(b)数据分别来自为LAMOST J093026.12+071221.0(obsid为805206193)和LAMOST J193205.73+402007.3(obsid为52803163)恒星光谱Fig.1 V-shape integration example graph in shape factor (a) and (b) side data respectively from LAMOST J093026.12+071221.0 and LAMOST J193205.73+402007.3 stellar spectra

当 $x_{ν_{11}}$ > $x_{ν_{12}}$ 且 $x_{ν_{11}}$ > $x_{ν_{22}}$ 时

$T_{递减} : x_{ν_{10}} > x_{ν_{20}} 且 (x_{ν_{21}} - x_{ν_{20}}) > (x_{ν_{22}} - x_{ν_{20}})$

当 $x_{ν_{21}}$ < $x_{ν_{31}}$ 且 $x_{ν_{22}}$ < $x_{ν_{32}}$ 时

$T_{递增} : x_{ν_{30}} > x_{ν_{20}} 且 0.3 (x_{ν_{22}} - x_{ν_{20}}) > (x_{ν_{31}} - x_{ν_{30}}) 或 x_{ν_{11}} > x_{ν_{22}} 且 (x_{ν_{11}} - x_{ν_{22}}) > (x_{ν_{11}} - x_{ν_{32}})$

1.2 尖峰深度

设w_i₁、 w_i₂、 w_i₃、 w_i₄、 w_i₅为第i条光谱在波段[us, ve]中形状因子W的五个端点所对应的波长, $x_{w_{i 1}}$ 、 $x_{w_{i 2}}$ 、 $x_{w_{i 3}}$ 、 $x_{w_{i 4}}$ 、 $x_{w_{i 5}}$ 为其各波长所对应的通量, 则W形深度d_w的判断准则s₃为

$s_{3} = \{\begin{array}{l} 0, & d_{w 1} > d_{w 2} \\ 1, & d_{w 1} \leq d_{w 2} \end{array}$ (4)

式(4)中, d_w₁和d_w₂分别表示W形最高点 $x_{w_{t}}$ 到中间峰 $x_{w_{i 3}}$ 的深度和中间峰 $x_{w_{i 3}}$ 到W形最低点 $x_{w_{b}}$ 的深度[式(5)— 式(8)]

$x_{w_{b}} = \min (x_{w_{i 2}}, x_{w_{i 4}})$ (5)

$x_{w_{t}} = \max (x_{w_{i 1}}, x_{w_{i 5}})$ (6)

$d_{w 1} = x_{w_{t}} - x_{w_{i 3}}$ (7)

$d_{w 2} = x_{w_{i 3}} - x_{w_{b}}$ (8)

且W形深度d_w参数为

$d_{w} = d_{w 1} + d_{w 2} = x_{w_{t}} - x_{w_{b}}$ (9)

记波段[us, ve]中, 由极大值a₁、 a₂和极小值b组成的V形(即向下尖峰)个数为m, 则第i条光谱的各尖峰深度d_i为

${{d}_{ik}}=\text{max}\left(\ \ {{x}_{{{\nu }_{ik1}}}}\ ,\ {{x}_{{{\nu }_{ik0}}}}\ ,\ {{x}_{{{\nu }_{ik2}}}} \ \ \right)-\text{min}\left(\ \ {{x}_{{{\nu }_{ik1}}}}\ ,\ {{x}_{{{\nu }_{ik0}}}}\ ,\ {{x}_{{{\nu }_{ik2}}}} \ \ \right)$(10)

式(10)中, i=1, 2, …, N; k=1, 2, …, m; ν _ik₁、 ν _ik₀、 ν _ik₂分别是第i条光谱在波段[us, ve]中第k个V形尖峰的左顶点、尖峰点和右顶点所对应的波长, $x_{ν_{ik 1}}$ 、 $x_{ν_{ik 0}}$ 、 $x_{ν_{ik 2}}$ 为其各波长所对应的通量。同时建立判断准则s₄和s₅, 分别判断最深尖峰d_i_max=max(d_ik), k=1, 2, …, m和第二深尖峰d_i_sec=max(d_il), l=C_kargmax[d_ik(k)]是否处于W形的波长范围(其中C表示补集), 从而确定带状深度, s₄和s₅具体如式(11)和式(12)

${{s}_{4}}=\left\{ \begin{array}{*{35}{l}} 0, & {{\nu }_{i\text{argmax}\left( {{d}_{ik}}\ \left( k \right) \right)\eta }}\ \ \not\subset {{w}_{if}} \\ 1, & {{\nu }_{i\text{argmax}\left( {{d}_{ik}}\ \left( k \right) \right)\eta }}\ \ \subset {{w}_{if}} \\ \end{array} \right.$(11)

$s_{5} = \{\begin{array}{l} 0, & ν_{ilη} ⊄ w_{if} \\ 1, & ν_{ilη} \subset w_{if} \end{array}$ (12)

式中的w_if={w_i₁, w_i₂, …, w_i₅}为形状因子W五个端点所对应波长的集合, l表示第二深尖峰的位置, 若第二深尖峰在最深尖峰的左侧, 则l=l; 若位于右侧, 则l=l+1, 即

$l = \{\begin{array}{l} l, & argmax (d_{il} (l)) < argmax (d_{ik} (k)) \\ l + 1, & argmax (d_{il} (l)) \geq argmax (d_{ik} (k)) \end{array}$ (13)

式(13)中, η =1, 0, 2; f=1, 2, …, 5。

1.3 W形宽度

分子带是两边高、中间低的类W兜形。本文利用三阶多项式对离散光谱进行拟合, 得到分子带中的回升部分曲线, 再根据投影映射得出与w_i₁相对应的值, 从而计算出其宽度E, 具体如下:

已知(w_if, $x_{w_{if}}$ ), f=1, …, 5是形状因子W的五个端点, 设端点(w_i₄, $x_{w_{i 4}}$ )到端点(w_i₅, $x_{w_{i 5}}$ )中间含有n₄₅个点, 为

$\underbrace{\left\{\left(\ \ u s_{w_{i4}}\ ,\ x_{{ius}_{w_{i4}}}\ \ \right)\ \left(\ \ u s_{w_{i4}}+1, x_{i\left(u s_{w_{i4}}+1\right)}\ \ \right) \cdots\left(\ \ u s_{w_{i \bar{j}}}\ , \ x_{i u s_{w_{ij}}}\ \right)\right\}}_{n_{45}}$

则

$\hat{x}={{a}_{0}}{{u}^{3}}+{{a}_{1}}{{u}^{2}}+{{a}_{2}}u+{{a}_{3}}$ (14)

再根据残差平方和求得式(14)的拟合系数为

$\varepsilon =\overset{n}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,{{({{\hat{x}}_{i}}-{{x}_{i}})}^{2}}=\overset{n}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,{{[\left( {{a}_{0}}u_{i}^{3}+{{a}_{1}}u_{i}^{2}+{{a}_{2}}{{u}_{i}}+{{a}_{3}} \right)-{{x}_{i}}]}^{2}}$(15)

令 $\partial ε / \partial a_{0} = 0; \partial ε / \partial a_{1} = 0; \partial ε / \partial a_{2} = 0$

且$\frac{\partial \varepsilon }{\partial {{a}_{j}}}=\overset{n}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,2u_{i}^{n-j}\left[ \left( {{a}_{0}}u_{i}^{3}+{{a}_{1}}u_{i}^{2}+{{a}_{2}}{{u}_{i}}+{{a}_{3}} \right)-{{x}_{i}} \right]=0$, 从而可以解出系数 $a_{0}$ 、 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ , 其次将 $x_{w_{i 1}}$ 向右平行投影到拟合曲线上, 设为 ${\vec{x}}_{w_{i 1}}$ , 即可得W形的宽度E为

$E = \{\begin{array}{l} {\vec{w}}_{i 1} - w_{i 1}, & {\vec{w}}_{i 1} \leq w_{i 5} \\ w_{i 5} - w_{i 1}, & {\vec{w}}_{i 1} > w_{i 5} \end{array}$ (16)

其中 ${\vec{w}}_{i 1}$ 表示通量 ${\vec{x}}_{w_{i 1}}$ 所对应的波长, 即

${\vec{w}}_{i 1} = \arg {\vec{x}}_{w_{i 1}}$ (17)

1.4 曲线趋势

由于存在噪声等因素, 使得分子带不再是平滑的类W兜形, 而是夹杂着许多起伏的类W坑形(见图2)。检验曲线趋势可以排除有着明显下降趋势的W形, 有效辨别真分子带和伪分子带。本文从W形波段的始末差距T₁和波段内的变化趋势T₂两个因素作为曲线趋势s_trend的判断依据, 具体如式(18)

$T_{1} = x_{w_{i 1}} - x_{w_{i 5}}$ (18)

	Figure Option View Download New Window
	图2 两图分别表现为平滑的类W兜形和类W坑形 (a): F8型恒星; (b): F3型恒星Fig.2 The two images show a smooth W-like hood and W-like pit, respectively (a): F8 type star; (b): F3 type star

始末差距T₁仅表征了W形波段的两个端点的差距, 不能反馈波段范围内的曲线变化趋势, 故采用累加法所计算得到的波段内递增T_increase和递减部分T_descend的差值绝对值T₂作为曲线趋势参数的参量之一[式(19)— 式(21)], 同时将其对比值作为曲线趋势的判断准则S_trend[式(22)]。

${{T}_{\text{descend}}}=\overset{n-1}{\mathop{\underset{j=1}{\mathop \sum }\,}}\,{{x}_{i\left( j+1 \right)}}-{{x}_{ij}},{{x}_{i\left( j+1 \right)}}-{{x}_{ij}}<0$(19)

${{T}_{\text{increase}}}=\overset{n-1}{\mathop{\underset{j=1}{\mathop \sum }\,}}\,{{x}_{i\left( j+1 \right)}}-{{x}_{ij}},{{x}_{i\left( j+1 \right)}}-{{x}_{ij}}\ge 0$(20)

${{T}_{2}}=\left| {{T}_{\text{descend}}}-{{T}_{\text{increase}}}\ \ \right|$(21)

$s_{trend} = \{\begin{array}{l} 0, & T_{descend} > T_{increase} \\ 1, & T_{descend} \leq T_{increase} \end{array}$ (22)

	Figure Option View Download New Window
	图3 两颗F型恒星的曲线趋势 (a): F0型恒星; (b): F5型恒星Fig.3 Curve trend of two F-type stars (a): F0 star; (b): F5 star

同时考察了截取波段[us, ve]中的曲线变化趋势情况, 以便作为所提取W形波段的参照量。

$T_{se} = x_{us} - x_{ve}; T_{te} = \max (x_{j}) - x_{ve} (j = 1, \dots, n)$ (23)

$T_{tl} = \max (x_{j}) - \min (x_{j})$ (24)

其中T_se、 T_te、 T_tl分别是波段[us, ve]的始末差距、最高点与末端的差距、最高点与最低点的差距, n为第i条光谱在波段[us, ve]中的n个点。

1.5 回升检验

曲线趋势仅表征曲线变化趋势, 为更进一步增加分子带的检测精度, 本文利用极值点分布对类W形进行了回升检验, 从而确保该波段是类W兜形, 具体如下:

根据一阶导数计算公式得x'_i(j)为

$x'_{i} (j) = \frac{x_{i} (j + 1) - x_{i} (j - 1)}{2 Δ λ}$ (25)

式(25)中, Δ λ 为波长间隔, 则极小值 ${\vec{x}}_{\min i}$ 为

${\vec{x}}_{\min i} = (x_{i j_{1}}, \dots, x_{i j_{n_{j}}}), x'_{i} (j) < 0, j \in [w_{i 3}, w_{i 5}]$ (26)

当极小值的个数m_min_i≥ 4时,

$S_{r} = \{\begin{array}{l} 0, & 其他 \\ 1, & \begin{array}{l} x_{i j_{1}} = \max ({\vec{x}}_{\min i}) 且 \\ x_{i j_{m_{\min i}}} = \max (C_{{\vec{x}}_{\min i}} \max ({\vec{x}}_{\min i})) \\ 或 x_{i j_{m_{\min i}}} = \max ({\vec{x}}_{\min i}) \end{array} \end{array}$ (27)

当极小值的个数m_min_i< 4时,

$S_{r} = \{\begin{array}{l} 0, & x_{i j_{m_{\min i}}} \neq \max ({\vec{x}}_{\min i}) \\ 1, & x_{i j_{m_{\min i}}} = \max ({\vec{x}}_{\min i}) \end{array}$ (28)

为了客观量化回升程度, 设r_mm、 r_em分别为回升部分[w_i₃, w_i₅]的最大极小值和最小极小值之差、 ${{x}_{i{{j}_{{{m}_{\ \text{min}i}}}}}}\ \ $和最小极小值之差在波段[us, ve]的最大值和最小值之差中的占比

${{r}_{mm}}=\frac{\text{max}\left( {{{{\vec{x}}}}_{\text{min}i}} \ \ \right)\ -\ \ \text{min}\left( {{{{\vec{x}}}}_{\text{min}i}} \ \ \right)}{\text{max}\left( {{x}_{j}} \right)-\text{min}\left( {{x}_{j}} \right)}, j\in \left[ {{w}_{i3}},{{w}_{i5}} \right]$(29)

${{r}_{em}}=\frac{{{x}_{i{{j}_{{{m}_{\ \text{min}i}}}}}}\ \ \ -\ \ \text{min}\left( {{{ {\vec{x}}}}_{\text{min}i}} \ \ \right)\ \ }{\text{max}\left( {{x}_{j}} \right)-\text{min}\left( {{x}_{j}} \right)}, j\in \left[ {{w}_{i3}},{{w}_{i5}} \right]$ (30)

2 恒星光谱w形分子带识别

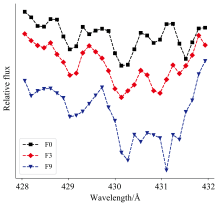
鉴于CH双原子分子引起的G分子带是F3型及晚期F型恒星的重要温度判别依据^[5], 且在恒星光谱型分类研究中, 光谱次型的分类相对光谱型的分类少。次型光谱特征相似度较高, 增加了分类难度, 对提取特征的准确性要求较高。因此选用F次型恒星光谱数据作为本次试验数据。为保证初始的光谱类型是较为准确的, 故实验数据选取了LAMOST DR8和GAIA DR2的F型恒星的交叉验证数据, 采集波段为370~900 nm, 采集样本点为3 748, 在550 nm处的分辨率约为1 800^[10]。本次实验共收集了7 407条光谱, 其中F0型1 602条, 非F0型5 805条。

2.1 W形检测

波段截取窗口大小n的取值范围为[10~100], 间距为10, 根据形状因子判断准则s₁和s₂遍历训练数据, 将每一遍历波段的判别数据作为训练特征对光谱数据中的F0型和非F0型恒星进行二分类, 根据分类准确度, 本文提取准确度较高的428~432 nm波段作为本次实验的检验波段(见图4)。

	Figure Option View Download New Window
	图4 F0型和非F0型在波段[428, 432] nm间的光谱曲线Fig.4 The spectral curves of F0 type and non-F0 type in the band [428, 432] nm

2.2 分子带特征

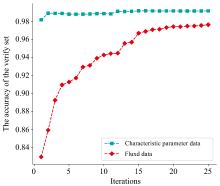
根据上述尖峰深度、 W形宽度、曲线趋势和回升检验四个参数的定义, 分别计算7 407条光谱在波段428~432 nm中的各项参数(训练特征), 再利用LightGBM模型对其进行二分类, 得到了99.16%的准确度, 而若直接使用通量数据作为训练数据, 其准确率仅为97.62%。这也从侧面验证了所提取特征和参数计算的准确性。

	Figure Option View Download New Window
	图5 训练数据分别为分子带特征参数和光谱通量的准确率对比图Fig.5 The training data are accuracy comparison graphs of molecular band characteristic parameters and spectral flux

3 结论与展望

基于W几何形的光谱分子带检测为光谱识别和分类提供了一种新的思路和方向, 根据分子带的形状构型识别出真分子带, 增强了光谱的分子带特征, 提高了恒星分类的准确度。此外对光谱数据采用曲线分析, 还可以达到量化分子带特征的目的, 在提高识别精度的同时, 亦可对比所得结果间各类参数的关系, 方便后续研究特征要素的重要性。

理论上综合考虑的光谱特征越多, 恒星分类准确率越高。本研究在一定程度上依赖于光谱的形状, 面对海量的光谱数据, 后续将结合深度学习模型对分子带进行自动识别和检测, 而不依赖光谱形状, 继续研究纯数据驱动下分子带在光谱中的作用和影响。

参考文献

文献列表

[1]	LI Shan-shan, FAN Dong-wei, CUI Chen-zhou, et al(李珊珊, 樊东卫, 崔辰州, 等). China Science and Technology Resources Review(中国科技资源导刊), 2022, 54(1): 47. [本文引用:1]
[2]	HUANG Yi-qi, ZHONG Jing, HOU Jin-liang(黄轶琦, 钟靖, 侯金良). Progress in Astronomy(天文学进展), 2020, 38(1): 69. [本文引用:1]
[3]	Paunzen E, Hümmerich S, Bernhard K. Astronomy and Astrophysics, 2021, 645: A34. [本文引用:1]
[4]	HUANG Run-qian(黄润乾). Stellar Physics(恒星物理). Beijing: China Science and Technology Press(北京: 中国科学技术出版社), 2006. [本文引用:1]
[5]	Gray R O, Corbally C. Stellar Spectral Classification. Princeton University Press, 2009. [本文引用:2]
[6]	Fan Zhou, Richard de Grijs, Chen Bingqiu, et al. The Astronomical Journal, 2016, 152(6): 208. [本文引用:1]
[7]	Knowles Adam T, Sansom A E, Coelho P R T, et al. Monthly Notices of the Royal Astronomical Society, 2019, 486(2): 1814. [本文引用:1]
[8]	Chen Shuxin, Sun Weimin, He Ying. Research in Astronomy and Astrophysics, 2022, 22(2): 025017. [本文引用:1]
[9]	XUE Ren-zheng, CHEN Shu-xin, HUANG Hong-ben(薛仁政, 陈淑鑫, 黄宏本). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(8): 2624. [本文引用:1]
[10]	Cui Xiangqun, Zhao Yongheng, Chu Yaoquan, et al. Research in Astronomy and Astrophysics, 2012, 12(9): 1197. [本文引用:1]

2022

0.0

... 引言自大型巡天项目(如LAMOST郭守敬望远镜、 SDSS斯隆数字巡天和GAIA盖亚卫星等)开展以来, 所收集到的恒星光谱已达千万量级^[1] ...

2020

0.0

... 黄轶琦等^[2]基于已知恒星参数信息的光谱通量数据, 构建纯数据驱动的The Cannon机器学习方法对恒星参数进行测量 ...

2021

0.0

... Paunzen等^[3]对汞锰星(CP3)进行证认时利用到了MKCLASS标准光谱库和LAMOST DR4中的光谱数据 ...

2006

0.0

... 恒星的光谱是由连续谱及在连续谱中的许多吸收线或发射线组成^[4] ...

2009

0.0

... 在这一背景下, Gray^[5]研究得到F型恒星在特定的有效温度下, 恒星大气中的某些化学元素可以形成双原子分子, 并能够持续存在, 从而导致分子带的出现, 特别是G波段的CH分子带, 这使得分子带成为了检验晚于F3型恒星的重要判别指标之一 ...

... 2 恒星光谱w形分子带识别鉴于CH双原子分子引起的G分子带是F3型及晚期F型恒星的重要温度判别依据^[5], 且在恒星光谱型分类研究中, 光谱次型的分类相对光谱型的分类少 ...

2016

0.0

... 文献[6,7,8,9]运用Lick线指数计算光谱特征, 但不能对光谱次型进行精确分类 ...

2019

0.0

... 文献[6,7,8,9]运用Lick线指数计算光谱特征, 但不能对光谱次型进行精确分类 ...

2022

0.0

... 文献[6,7,8,9]运用Lick线指数计算光谱特征, 但不能对光谱次型进行精确分类 ...

2019

0.0

... 文献[6,7,8,9]运用Lick线指数计算光谱特征, 但不能对光谱次型进行精确分类 ...

2012

0.0

... 为保证初始的光谱类型是较为准确的, 故实验数据选取了LAMOST DR8和GAIA DR2的F型恒星的交叉验证数据, 采集波段为370~900 nm, 采集样本点为3 748, 在550 nm处的分辨率约为1 800^[10] ...