试验于2022年4月至5月在西北农林科技大学农业农村部物联网重点实验室(36° 16'N, 108° 4'E)进行。 以杭茄1号为试验材料, 采用基质育苗方式, 待幼苗生长至三叶一心时期, 选取生长健康、 长势一致的60株幼苗移栽至珍珠岩固体基质中, 进行无土栽培管理。 以日本圆试营养液配方(氮素浓度17.5 mmol· L^-1)为对照, 采用单因素试验设计方法, 设置4组氮素浓度梯度(N0, N1, N2, N3), 分别为0、 8.75、 17.5和26.25 mmol· L^-1, 培养茄子幼苗。 培养期间每2 d更换一次营养液, 保持营养液中各元素相对恒定。 待培养21 d后, 将相同梯度培养下的同一叶位3片叶子作为一个样本, 测定其高光谱信息和氮含量, 样本共计102。

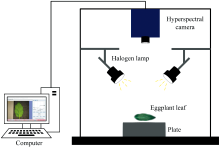
试验使用可见-近红外高光谱成像系统(SOC710-VP, SurfaceOptics, 美国), 可采集光谱范围为370~1 050 nm, 光谱分辨率为1.3 nm, 采集系统如图1所示。 测量前对光源预热30 min, 调整高光谱相机镜头与载物台距离为0.5 m, 卤素灯与载物台距离为0.3 m, 保证采集样本光度曲线在2 000~3 000 counts之间, 以获取具有高信噪比的HSI数据。 设置高光谱图像采集曝光时间为25 ms, 波段数为512, 扫描速度每秒30行, 原始图像分辨率为696像素× 520像素。 由于仪器采集光谱信息的首尾部分波段噪声较大, 所以选取400~1 000 nm的448个波段光谱数据进行后续的分析和处理。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 高光谱成像采集系统Fig.1 Hyperspectral images acquisition system

利用SARnal710e软件对高光谱图像进行灰板校正, 得到原始光谱反射率数据。 选取每个样本叶片光照均匀、 叶面平整的区域作为感兴趣区域(region of interest, ROI), 计算ROI 的平均光谱反射率作为该样本的有效光谱数据。 此外, 随机选取每个样本叶片HSI数据中20个像素级光谱数据作为训练CAE网络的无目标值数据集。

叶片氮含量测定方法采用凯氏定氮法。 将采集光谱信息后的鲜叶, 于105 ℃温度下杀青30 min, 然后调整至75 ℃持续烘干48 h至恒重。 由于检测的最低干重限制(0.1 g), 将烘干后的叶片样本(3片一组)研磨粉碎, 使用全自动凯氏定氮仪(KjeltecTM8400, Foss, 丹麦)测定各样本的氮含量, 共计得到102个叶片氮含量值。

为消除仪器暗电流和噪音以及外界杂散光等因素对特征提取和模型性能的影响, 采用多元散射校正算法(multiplicative scatter correction, MSC)对原始光谱数据进行预处理。 此外, 在样本集划分时为更好的表征样本分布, 提高预测模型的稳定性, 采用共生距离算法(sample set partitioning based on joint x-y distance, SPXY), 将102个样本以4∶ 1的比例划分为训练集和测试集。

原始光谱数据冗余度和共线性高, 需进行特征光谱提取以减少计算量, 降低建模输入变量维度。 采用RF与CARS算法进行特征波长选取, 保留具有代表性的波长作为PLSR输入, 建立茄子叶片氮含量预测模型, 并与利用HSI-CAE特征提取方法建立的预测模型性能进行对比。 其中, RF算法通过迭代循环保留选择概率较大的波长作为特征变量, 设定迭代次数为1 000, 主成分数为10。 CARS算法使用竞争性学习方法自适应调整变量权重, 剔除贡献度较小的变量, 并通过循环迭代最小化交叉验证均方差(root mean square error of cross validation, RMSECV), 确定最优变量子集。 设定抽样次数为50, 并通过十折交叉验证计算RMSECV值。

1.6.1 卷积自编码网络

自动编码网络是一种无监督学习算法, 能够从大量无标签数据中提取有效特征, 实现数据降维。 CAE是自动编码器的一种延伸, 二者的网络结构相似。 CAE在构建编码器时采用卷积层和池化层代替传统编码器的全连接层, 使用反卷积层与上采样层建立解码器以恢复输入数据, 并通过最小化重构数据与原始数据的误差实现网络参数优化^[9]。 其中, 卷积层具有权值共享与局部感知的特点, 能够有效提取原始数据的特征。 池化层能够将提取特征降维, 去除噪声和冗余信息, 减少模型参数, 加快网络模型的计算速度, 提高模型的泛化能力^[10]。

对于输入的无目标值光谱数据, 在编码器网络中通过卷积运算进行非线性映射提取特征, 再通过池化运算降低数据维度, 得到数据深度特征。 对任意一个单通道输入x^k, 其卷积运算的映射为h^k, 池化运算输出深度特征为y^k, f为激活函数, 则卷积运算与池化运算公式分别为

hk=f(w1k* xk+b1k)(1)

yk=f(w2kp(hk)+b2k)(2)

式(1)和式(2)中, * 表示卷积运算, w1k与 b1k为卷积运算权重与偏差。 p(· )表示池化运算, w2k与 b2k为池化运算权重与偏差。

解码器网络是编码器网络的逆过程, 以深度特征为输入, 通过上采样层增加数据维度, 得到与原始数据规模相同的输出${{\hat{g}}^{k}}$, 再通过反卷积层重构输入数据${{\hat{x}}^{k}}$。 上采样运算与反卷积运算公式分别为

${{\hat{g}}^{k}}=f\left( \hat{w}_{2}^{k}u\left( {{y}^{k}} \right)+\hat{b}_{2}^{k} \right)$ (3)

${{\hat{x}}^{k}}=f\left( \hat{w}_{1}^{k}* {{{\hat{g}}}^{k}}+\hat{b}_{1}^{k} \right)$ (4)

式(3)和式(4)中, u(· )表示上采样运算, $\hat{w}_{2}^{k}$与$\hat{b}_{2}^{k}$为上采样运算权重与偏差。$\hat{w}_{1}^{k}$与$\hat{b}_{1}^{k}$为反卷积运算权重与偏差。

1.6.2 网络结构设计

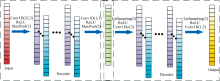
CAE网络由编码器与解码器构成, 编码器实现对输入数据的特征提取与降维, 解码器将提取出的深度特征重构以还原输入数据。 基于tensorflow框架与keras深度学习库搭建一维CAE网络, 如图2所示。 由于网络深度与输出特征维度不同均会影响光谱数据深度特征的提取, 因此需对比不同网络提取深度特征的建模效果, 选择最优CAE网络结构。 设计四种CAE网络, 编码器中卷积层与池化层数分别为5, 4, 3, 2。 解码器结构与编码器对称, 反卷积层数与上采样层数分别为5, 4, 3, 2。 其中, 五层卷积层的滤波器数量依次为32, 16, 8, 4, 1, 五层反卷积层的滤波器数量依次为4, 8, 16, 32, 1, 并设定不同深度CAE网络为依次去掉具有最大滤波器的卷积层与反卷积层, 其输出深度特征维度分别为112, 56, 28, 14。 考虑使用较大卷积核会使网络训练参数增加, 延长网络训练时间, 故卷积核大小均设定为3, 步长为1。 池化层与上采样层窗口大小均设定为2, 步长为1。 在上述每个卷积层后与反卷积层前设置线性整流函数(rectified linear units, ReLU)层以避免梯度消失, 加快网络收敛速度。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 CAE网络模型结构Fig.2 Structure of CAE network model

在网络训练过程中, 采用自适应矩估计(adaptive moment estimation, Adam)优化器, 学习率设定为0.001, 并采用均方误差(mean square error, MSE)作为损失函数, 计算CAE网络重构光谱数据与原始光谱数据之间的差异, 优化模型参数, 提高编码器输出特征的表达能力, 其表达式为

$L\left( \hat{x}, x \right)=\frac{1}{n}\overset{n}{\mathop{\underset{i}{\mathop \sum }\, }}\, {{({{\hat{x}}_{i}}-{{x}_{i}})}^{2}}$ (5)

式(5)中:${{\hat{x}}_{i}}$为重构光谱数据, x_i为原始光谱数据, n为训练样本个数。

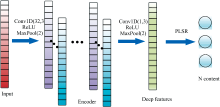
为高效利用高光谱数据, 提取其有效信息, 提出HSI-CAE深度特征提取方法。 首先使用叶片像素级HSI数据训练CAE网络, 使其具备良好的特征提取能力。 之后去掉网络解码器部分, 将叶片ROI区域平均光谱输入编码器, 经卷积与池化运算输出深度特征, 作为PLSR输入, 建立CAE-PLSR氮含量预测模型, 模型结构如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 CAE-PLSR氮含量预测模型Fig.3 CAE-PLSR prediction model of N content

PLSR是多因变量与多自变量建模分析中常用的多元线性回归方法, 处理高维度、 小样本光谱数据的表现优越。 PLSR具有主成分分析与典型相关性分析的特点, 能够同时将自变量光谱矩阵与因变量浓度矩阵分解, 分别投影到低维空间, 通过寻找最大协方差项获取多个潜在变量, 建立回归预测模型^[11]。

为评估建立模型的预测精度及泛化能力, 采用决定系数(coefficient of determination, R²)与均方根误差(root mean square error, RMSE)来综合评价, 其计算方法如式(6)和式(7)所示

${{R}^{2}}=1-\frac{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\, {{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}}{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\, {{({{y}_{i}}-{{{\bar{y}}}_{i}})}^{2}}}$ (6)

$\text{RMSE}=\sqrt{\frac{\overset{n}{\mathop{\mathop{\sum }_{i=1}}}\, {{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}}{n}}$ (7)

式(6)和式(7)中, n为样本个数, y_i、${{\hat{y}}_{i}}$、${{\bar{y}}_{i}}$分别是样本的实测值、 预测值和平均值。

采集四个施氮梯度培养下的茄子叶片作为试验样本集, 通过凯氏定氮法测定叶片样本氮含量, 采用SPXY算法按4∶ 1比例划分建立模型的训练集与测试集。 对各样本集氮含量进行统计分析, 其分布结果如图4所示。 总样本集氮含量分布基本符合正态分布, 训练集与测试集的氮含量中位数与均值相近。 此外, 测试集分布均匀, 表明SPXY算法划分的样本集具有良好的差异性与代表性, 有利于提高氮含量预测模型的稳定性与鲁棒性。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各样本集氮含量分布Fig.4 Nitrogen content distribution of each set

计算各样本ROI区域平均光谱值作为该样本有效光谱数据, 所有样本光谱曲线如图5(a)所示。 各叶片光谱曲线表现出相似的趋势, 在550 nm附近处的反射峰是由于叶绿素对绿光具有较强的反射作用, 470~510和650~700 nm两处的波谷分别是由叶绿素对蓝光和红光的强吸收造成, 750~900 nm的高反射率平台是由短波近红外光在叶片内部多次散射引起。 光谱反射率是反映叶片营养状况的重要指标, 由于氮素营养缺乏会引起叶片色素沉积变化与结构变形, 所以四个氮素梯度培养下的样本平均光谱曲线存在显著差异, 如图5(b)所示。 其中, N0与N1梯度培养下的样本由于缺乏氮素导致叶绿素、 类胡罗卜素等合成受阻, 使得叶片对可见光的吸收作用减小, 故光谱反射率较高^[12]。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 茄子叶片光谱曲线 (a): 原始光谱曲线; (b): 平均光谱曲线; (c): MSC预处理Fig.5 Spectral curve of eggplant leaves (a): Raw spectra samples; (b): Mean spectra of samples; (c): Spectra preprocessed with MSC

MSC预处理将样本集的平均光谱作为标准光谱, 对各光谱曲线进行校正处理, 消除由散射水平不同造成的光谱差异, 减小噪声影响, 得到更为集中的反射光谱, 如图5(c)所示。

利用CARS算法筛选特征波长结果如图6(a, b)所示。 随着采样次数的增加, 基于变量子集建立的PLSR模型的RMSECV值逐渐减小。 在第27次采样时, RMSECV达最小值3.077, 表明在采样过程中剔除了大量与预测目标值无关的变量和部分共线变量。 第27次采样后, RMSECV值波动上升, 表明光谱数据中某些关键信息被剔除, 导致PLSR模型预测精度下降。 因此, 将第27次采样选取的特征波长作为建立氮含量预测模型的最优变量子集, 共计24个波段。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 CARS特征波长提取结果 (a): RMSECV变化; (b): 特征波长分布Fig.6 Results of characteristic wavelength selection by CARS (a): Variation of RMSECV; (b): Characteristic wavelengths distribution

利用RF算法筛选特征波长结果如图7(a, b)所示。 为提高选取特征波长组合的可靠性, 计算1 000次迭代循环中各波长被选择的平均概率作为选择依据, 降低随机初始化变量子集的影响。 由于波长被选概率高代表其具有较高的适应度, 设定特征波长选择概率阈值为0.2, 最终选取特征波段数量共计30个。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 RF特征波长提取结果 (a): 各波段选择概率; (b): 特征波长分布Fig.7 Results of characteristic wavelength selection by RF (a): Selection probability of each wavelength; (b): Characteristic wavelengths distribution

CARS与RF算法选取的特征波段主要分布在“ 绿峰” (近550 nm), “ 红谷” (近680 nm), “ 红边” (680~760 nm)和近红外波段(800~1 000 nm)。 光谱400~1 000 nm不存在对叶片氮含量具有直接光吸收敏感性的波段, 但所选特征波段与类胡萝卜素、 叶绿素以及叶片的含水率密切相关^{[13, 14, 15]}, 可通过其反射率变化间接反演叶片的氮含量。

在CAE网络训练过程中, 首先将2 040个像素级光谱数据进行标准化预处理, 缩放原始数据特征并消除量纲影响, 然后按7∶ 3比例将其分为训练集与验证集作为网络训练的无目标值输入。 编码器利用卷积层提取光谱数据的特征, 并通过卷积后的池化运算减少特征数量, 实现深度特征的提取。 在解码器中, 采样反卷积与上采样运算将深度特征重构为全波段光谱数据。 以四层CAE为例, 其编码器网络结构为448-224-112-56-28。 设定迭代次数为600, 训练初期MSE快速下降, 当迭代次数大于100后, 训练集与验证集误差值均趋于收敛, 最终验证集误差为0.046, 如图8(a)所示。 将重构光谱数据反标准化, 还原为原始数据量级, 并绘制原始平均光谱曲线与重构平均光谱曲线, 如图8(b)所示。 可见重构平均光谱曲线与原始平均光谱曲线几乎重合, 重构误差较小, 表明训练后的编码器具有良好的特征提取与降维能力, 提取的深度特征能够有效表征原始数据。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 CAE训练结果 (a): 训练重构误差; (b): 重构光谱与原始光谱Fig.8 Training results of CAE (a): Reconstruction error of training; (b): Original and reconstructed mean spectra

将样本的有效光谱数据作为训练后编码器网络的输入, 实现光谱数据的特征提取与降维。 四种CAE网络提取深度特征数量分别为112、 56、 28、 14, 其特征曲线如图9(a— d)所示。 深度特征曲线随CAE编码器网络深度的增加与输出特征的减少变得更加抽象简单。 为确定最优CAE网络结构, 并验证提取的特征变量含有叶片氮含量相关信息, 需利用各维度深度特征分别建立预测模型并比较模型性能。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 CAE编码器输出特征Fig.9 Output features of CAE encoders

将各深度CAE编码器输出深度特征作为自变量, 氮含量值作为因变量, 建立PLSR预测模型, 并通过R²与RMSE评价模型的精度及泛化能力, 结果如表1所示。 基于不同深度特征数量建立的模型均有较高的预测精度R²> 0.85, 其中以28维特征建立的模型测试集R²为0.910 2, RMSE为3.118 9 mg· g^-1, 预测性能最优。 表明CAE提取的深度特征中含有与叶片氮含量高度相关的信息, 验证了HSI-CAE特征提取方法的可行性。 当输出特征维度进一步减小时, 测试集精度下降, 可能是编码器过度的池化运算剔除了有效信息, 所以CAE编码器最优结构为448-224-56-28。

表1

Table 1

表1(Table 1)

表1 CAE输出深度特征PLSR建模结果 Table 1 Results of PLSR with different CAE Output deep features 特征 数量 训练集 测试集 R2 RMSE/ (mg· g-1) R2 RMSE/ (mg· g-1) 112 0.933 8 2.390 9 0.863 9 3.838 3 56 0.938 1 2.311 0 0.882 3 3.570 2 28 0.942 4 2.229 3 0.910 2 3.118 9 14 0.935 6 2.361 5 0.868 8 3.584 2

表1 CAE输出深度特征PLSR建模结果 Table 1 Results of PLSR with different CAE Output deep features

传统特征波长提取方法与CAE网络均实现了对原始光谱数据的降维。 通过CARS、 RF算法提取特征波长后, 全波段光谱数据由448维降低到24维与30维。 采用CAE编码器提取光谱数据的深度特征共计28个。 将全波长光谱数据、 特征波长和深度特征分别作为PLSR的输入, 建立氮含量预测模型, 结果如表2示。

表2

Table 2

表2(Table 2)

表2 不同特征提取方法PLSR建模结果 Table 2 Modeling results of PLSR with different feature selection methods 方法 特征 数量 训练集 测试集 R2 RMSE/ (mg· g-1) R2 RMSE/ (mg· g-1) Full 448 0.922 7 2.581 9 0.847 8 4.059 3 CARS 24 0.942 5 2.228 5 0.868 9 3.766 9 RF 30 0.947 5 2.128 1 0.877 0 3.649 1 CAE 28 0.942 4 2.229 3 0.910 2 3.118 9

表2 不同特征提取方法PLSR建模结果 Table 2 Modeling results of PLSR with different feature selection methods

由表2可以看出, 全波段光谱数据建立的氮含量预测模型受噪声及无关变量影响, 精度最差, 测试集R²为0.847 8, RMSE为4.059 3 mg· g^-1。 采用CARS与RF特征波长提取算法, 模型自变量个数分别减少了94.64%与93.30%, 有效去除了光谱数据中的冗余信息, 保留了与叶片氮含量密切相关的波段, 降低了模型的计算量。 同时, CARS-PLSR和RF-PLSR模型训练集R²在0.94以上, 测试集R²达0.85以上, 预测精度有所提高, 但模型泛化能力较差, 存在轻微过拟合现象。

利用CAE编码器提取的深度特征建立CAE-PLSR预测模型, 其测试集R²为0.910 2, RMSE为3.118 9 mg· g^-1, 预测精度显著高于CARS-PLSR和RF-PLSR模型。 这是由于CAE是一种非线性降维方法, 利用卷积运算能够有效捕捉光谱数据各波段间的相关性, 保留光谱数据真实内在结构信息。 同时, 卷积运算将光谱相邻波段的数据平滑, 降低了特征提取时噪声及冗余信息干扰。 CAE编码器交替进行卷积运算与池化运算, 在提取主要特征的同时降低数据维度, 获取了能够良好表达光谱信息的深度特征。 其次, 利用大量随机像素级光谱数据训练CAE网络, 充分考虑了叶片局部光谱特征, 有助于揭示HSI数据的全局信息, 避免网络产生过拟合现象, 提高了编码器的特征提取能力。 因此, CAE-PLSR模型具有较强的泛化能力, 测试集表现优于CARS-PLSR和RF-PLSR模型。