LIF系统或装置中的激光源发射激光到乳化液上, 在某个λ 波长会接收到激发的荧光。 LIF探测器在λ 波长接收到的油膜激发的荧光强度K可通过式(1)计算^[6]

K=ηP0{1-exp[-(ke+kλ)d]}(1)

式(1)中, P₀为激光入射能量, k_e和k_λ 分别为乳化液在激发光波长和λ 波长的消光系数, d为油膜厚度, η 为在波长λ 处的水包油乳化液的荧光转换效率。

然而通过我们的验证, 此公式并不能较准确地对深度较大的水包油乳化液进行描述, 因此本文推导出一个新的计算方法。

在水包油乳化液中, 受到吸收的影响, 达到深度x的激光强度减弱为

Px=P0(1-ρae)exp[-αex](2)

式(2)中, ρ _ae为大气和水包油乳化液界面的反射系数, α _e为乳化液在激发光波长的吸收系数。 考虑到荧光的发射具有各向同性, 导致散射的光也可能产生荧光被LIF探测器接收到, 因此这里没有使用消光系数(吸收系数和散射系数之和)。

设ρ _q为量子荧光产率, p(x)为接收器接收到的荧光占所有荧光的比例。 则激光在x处激发的在接收器接收角度范围内的荧光为

Kx=P0(1-ρae)exp[-αex]ρqp(x)(3)

距离水包油乳化液和海水界面距离为x的荧光传播到水面, 光强度变换为

K=Kxexp[-αλx](4)

式(4)中, α _λ 为乳化液在λ 波长的吸收系数。 这里没有使用消光系数的原因同样是荧光发射的各向同性, 有荧光被散射出接收范围, 同样有原本在接收范围之外的荧光被散射进接收范围。

对于厚度为d的水包油乳化液层, 探测器接收到的总荧光

K=∫0dP0(1-ρae)exp[-αex]ρqp(x)exp[-αλx]dx=∫0dP0(1-ρae)ρqp(x)exp[-(αe+αλ)x]dx(5)

水包油乳化液和海水的界面处会对光线形成反射, 水包油乳化液和空气界面也会对荧光反射, 这两者在一定程度上会相互抵消, 因此这里不纳入对反射的计算。 真实环境中, 光线甚至可能会多次反射, 这里通过简化计算而尽可能准确地描述真实环境中的情况。

设探测器接收范围的直径为l, 在给定弦长l和弦到圆心距离x时, 可求得圆的半径r为

$r=\sqrt{{{x}^{2}}+\frac{{{l}\ ^{2}}}{4}}$(6)

由于荧光发射的各向同性, 球冠面积所占整个球面积的比例, 即为探测器接收的荧光占全部荧光的比例

$p\left( x \right)=\frac{2 \pi r\left( r-x \right)}{4 \pi {{r}^{2}}}=\frac{1}{2}-\frac{x}{2\sqrt{{{x}^{2}}+\frac{{{l}\ ^{2}}}{4}}}$(7)

代入式(5)可得

$K=\underset{0}{\overset{d}{\mathop \int }}\,{{P}_{0}}\left( 1-{{\rho }_{ae}} \right){{\rho }_{q}}\left( \frac{1}{2}-\frac{x}{2\sqrt{{{x}^{2}}+\frac{{{l}\ ^{2}}}{4}}} \right)\cdot \text{exp}\left[ -\left( {{\alpha }_{e}}+{{\alpha }_{\lambda }} \right)x \right]\text{d}x$(8)

对于同种油品, α _e、 α _λ 与乳化时间、 波长、 浓度有关, 与厚度d无关。

当乳化液层的厚度d增大时, K会增大。 厚度d增大到一定程度时, K/P₀几乎不再变化, 此时荧光强度K出现饱和。 设饱和因子s=(K/P₀)', 当s小于ε 时荧光强度基本不再有变化, 从而出现饱和。 称s=ε 时的厚度为饱和厚度。

$s=\{\underset{0}{\overset{d}{\mathop \int }}\,(1-{{\rho }_{ae}}){{\rho }_{q}}\left( \frac{1}{2}-\frac{x}{2\sqrt{{{x}^{2}}+\frac{{{l}\ ^{2}}}{4}}} \right)\cdot \text{exp}\left[ -\left( {{\alpha }_{e}}+{{\alpha }_{\lambda }} \right)x \right]\text{d}x\}'$(9)

根据微积分第一基本定律, 可得

$s=\left( 1-{{\rho }_{ae}} \right){{\rho }_{q}}\left( \frac{1}{2}-\frac{d}{2\sqrt{{{d}^{2}}+\frac{{{l}\ ^{2}}}{4}}} \right)\text{exp}\left[ -\left( {{\alpha }_{e}}+{{\alpha }_{\lambda }} \right)d \right]$(10)

设l为10 mm, ε 为10^-9。 荧光量子产率ρ _q作为油品的参数, 与深度无关。 计算出当前乳化液在激发波长和λ 波长的吸收系数α _e、 α _λ , 即可求得出现荧光强度饱和的乳化液厚度。

使用1号油、 2号油和海水的参数, 由米氏散射(Mie scattering)理论计算得出水包油乳化液油滴粒子在不同波长、 不同乳化时间的吸收效率, 然后根据吸收效率和水包油乳化液的浓度计算出水包油乳化液的吸收系数^[7]。 得到α _e和α _λ 之后, 即可根据上述公式求得饱和厚度。

求出1号油和2号油在不同浓度和乳化时间下水包油乳化液的饱和厚度, 如表1和表2所示。 其中浓度单位为10^-6体积分数。 由表1、 表2中的数据可以看出: 饱和厚度随着浓度的增加而降低, 随着乳化时间的增加而降低, 随着油品透明度的增加而增加。

表1

Table 1

表1(Table 1)

表1 不同浓度和乳化时间下的1号油乳化液的饱和厚度 Table 1 Saturation thickness of No.1 oil emulsion under different concentrations and emulsification time 浓度 /10-6 乳化0天 /m 乳化1天 /m 乳化2天 /m 乳化7天 /m 1 1.85 1.60 1.52 1.38 2 1.35 1.13 1.05 0.94 3 1.08 0.89 0.83 0.73 4 0.92 0.74 0.68 0.60 5 0.80 0.64 0.59 0.52 10 0.50 0.39 0.36 0.31 20 0.30 0.23 0.21 0.18 50 0.15 0.11 0.10 0.09

表1 不同浓度和乳化时间下的1号油乳化液的饱和厚度 Table 1 Saturation thickness of No.1 oil emulsion under different concentrations and emulsification time

表2

Table 2

表2(Table 2)

表2 不同浓度和乳化时间下的2号油乳化液的饱和厚度 Table 2 Saturation thickness of No.2 oil emulsion under different concentrations and emulsification time 浓度 /10-6 乳化0天 /m 乳化1天 /m 乳化2天 /m 乳化7天 /m 1 3.65 3.56 3.54 3.52 2 3.37 3.23 3.20 3.17 3 3.14 2.96 2.93 2.89 4 2.94 2.74 2.71 2.66 5 2.77 2.55 2.52 2.47 10 2.17 1.93 1.90 1.85 20 1.56 1.34 1.31 1.26 50 0.90 0.75 0.73 0.70

表2 不同浓度和乳化时间下的2号油乳化液的饱和厚度 Table 2 Saturation thickness of No.2 oil emulsion under different concentrations and emulsification time

不同波长对饱和厚度有影响。 比如表3列出了给定乳化时间为0天, 不同浓度和一部分波长下的1号油乳化液的饱和厚度。

表3

Table 3

表3(Table 3)

表3 乳化时间为0天, 不同浓度和λ 波长下的1号油乳化液的饱和厚度 Table 3 Saturation thickness of No.1 oil emulsion with emulsification time of 0 days at different concentrations and λ wavelengths 浓度 /10-6 波长 450 nm /m 波长 500 nm /m 波长 550 nm /m 波长 600 nm /m 波长 650 nm /m 波长 700 nm /m 1 1.63 1.74 1.85 1.83 1.80 1.67 2 1.15 1.24 1.33 1.35 1.34 1.27 3 0.9 0.98 1.05 1.08 1.08 1.04 4 0.75 0.81 0.88 0.91 0.91 0.89 5 0.65 0.70 0.76 0.79 0.80 0.78 10 0.39 0.43 0.47 0.49 0.50 0.49 20 0.23 0.26 0.28 0.29 0.30 0.30 50 0.11 0.12 0.14 0.14 0.15 0.15

表3 乳化时间为0天, 不同浓度和λ 波长下的1号油乳化液的饱和厚度 Table 3 Saturation thickness of No.1 oil emulsion with emulsification time of 0 days at different concentrations and λ wavelengths

如表3中所示, 相同浓度和乳化时间的1号油乳化液, 通常随着波长的增加呈现饱和深度先上升后下降的趋势。 表1和表2中列出的是450~700 nm波段全部达到饱和厚度时计算出的数值。

从表1中的数据可以看出: 所有条件下的1号油水包油乳化液的饱和厚度小于2 m。 根据Cormack等的研究结果^[8]: 水体被油膜污染2小时后水体污染厚度约为2~15 m; 20 h后水体污染厚度约为2 m。 对比上述数据可知, 海中更常见的深色石油的水包油乳化液, LIF接收到的荧光强度通常会出现饱和。

基于蒙特卡洛方法对海面溢油进行仿真研究是一种公认的有效的方法^{[7, 9, 10, 11]}。 激光照射水包油乳化液激发的荧光, 受油品、 乳化时间、 浓度、 厚度等的影响。 影响因素较多导致全面的实验较为困难, 仿真方法提供了对水包油乳化液进行分析的一个途径。

激光照射激发的荧光, 可由双向反射再辐射分布函数(BRRDF)表征。 相同探测接收条件下, 在某一接收波长处, LIF探测系统接收到的光功率与X_BRRDFcosθ _rcosθ _i成正比^{[7, 9]}。 其中X_BRRDF表示水包油乳化液在不同探测参数下计算出的BRRDF, θ _r为出射天顶角, θ _i为入射天顶角。 令$\widetilde{K}={{X}_{B}}RRDF\cos {{\theta }_{r}}\cos {{\theta }_{i}}$, 用于表示仿真的LIF探测系统接收到的荧光强度。

本文参照张晓丹等^[9]给出的相关油品数据以及仿真方法和对水包油乳化液BRRDF模型进行仿真, 对前面计算出的结果进行验证。 激发波长设定为400 nm, λ 波长设定为在[450 nm, 700 nm]区间内的26个数值(每间隔10 nm取1个), 每束光的光子数量设定为10⁷个。 计算出表1和表2中列出的所有浓度和乳化时间条件下, [0.01 m, 4.0 m]范围内60个采样厚度的水包油乳化液的荧光强度$\widetilde{K}$。

荧光强度$\widetilde{K}$的计算中, 每束光的光子数量有限(设定为10⁷个), 会有小的误差, 因此不足以支持非常精确的饱和厚度的计算。 然而, 通过对比各个波长下的饱和深度数据和相应条件下荧光强度$\widetilde{K}$随不同厚度的变化曲线, 可以看出结果全部符合。

比如图1中显示了两个条件下荧光强度$\widetilde{K}$随不同厚度变化的曲线。 图1(a)为条件A(1号油, 乳化时间0天, 浓度3× 10^-6, λ 波长450 nm)下乳化液厚度与$\widetilde{K}$的关系。 图1(b)为条件B(1号油, 乳化时间0天, 浓度50× 10^-6, λ 波长700 nm)下乳化液厚度与$\widetilde{K}$的关系。

图1

Fig.1

	Figure Option ViewDownloadNew Window
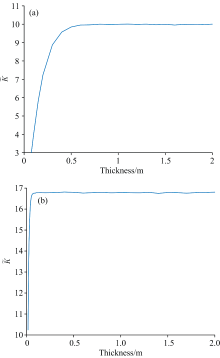	图1 不同条件下的乳化液厚度与$\widetilde{K}$的关系 (a): 条件A; (b): 条件BFig.1 Relationship between emulsion thickness and $\widetilde{K}$ under different conditions (a): Condition A; (b): Condition B

从图1(a)中可以看出, 在厚度0.9 m附近$\widetilde{K}$开始饱和; 从图1(b)中可以看出, 在厚度0.15 m附近$\widetilde{K}$开始饱和。 这两个结果与表3中的数据相符合。 本文的ε 的取值很小, 从图中可以看出, 达到饱和厚度时人眼基本看不出荧光强度曲线的明显变化了。

荧光出现饱和之后, 不同浓度乳化液的光谱的独特程度是否可以用来鉴别不同浓度的乳化液。 为了验证这一点, 本文设计了一个全连接神经网络。 深层神经网络具有优秀的特征发现能力, 可以较好地分辨出光谱是否具有鉴别能力, 然而过多的层次会带来过拟合现象的发生。 因此这里使用了一个适中的四层神经元的神经网络对水包油乳化液荧光光谱的识别能力进行分析。 本文设计的神经网络如图2所示。 输入层的输入为26个λ 波长(450~700 nm, 每间隔10 nm取1个)的$\widetilde{K}$数值。 第一个隐藏层50个神经元, 第二个隐藏层5个神经元, 第三个隐藏层10个神经元。 输出层只有一个神经元, 其输出值表示浓度。 三个隐藏层的激活函数使用ReLU, 输出层无激活函数。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 神经网络结构Fig.2 Neural network structure

对于全连接神经网络, 如果不考虑样本的特征的干扰因素, 那么两层神经元(一层隐藏层加一层输出层)的网络能够以任意精度逼近连续分类函数; 三层神经元的网络能够以任意精度逼近任意分类函数。 由于通常无法判断出样本的分布规律以及最适合的分类函数形式, 因此可以采用最少三层神经元的网络结构。 如果考虑到不同特征之间可能存在相关性等干扰因素, 需要再增加层次从而增加网络自动发现特征的能力。 此神经网络的作用是验证荧光光谱的识别能力, 如果神经网络的表示能力不足会影响对荧光光谱识别能力的判断。 因此这里使用了三层隐藏层, 从而对特征进行一定的自动编码。 神经网络的训练数据使用一系列厚度{0.05, 0.5, 1.9 m}和浓度{1× 10^-6, 2× 10^-6, 3× 10^-6, 4× 10^-6, 5× 10^-6, 10× 10^-6, 20× 10^-6, 50× 10^-6}组合条件对应的$\widetilde{K}$数据作为神经网络的输入, 这些数据下的真实浓度作为神经网络的目标输出。 测试使用厚度{0.06, 0.07, 0.08, 0.09, 0.1, 0.15, 0.2, 0.3, 0.4, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8 m}和浓度{2× 10^-6, 3× 10^-6, 4× 10^-6, 20× 10^-6}组合条件下的$\widetilde{K}$数据作为网络的输入, 这些数据对应的真实浓度作为神经网络的目标输出。 此处没使用浓度超过50× 10^-6的样本, 这是因为真实环境中很少出现如此高浓度的水包油乳化液^[8]。

对上述数据进行筛选, 去除那些没有达到饱和厚度的数据, 保留那些达到饱和厚度的数据。 使用这些训练数据对神经网络进行训练之后, 统计出神经网络对测试数据计算输出的浓度与目标输出(即真实浓度)的差值。 训练之后使用测试数据进行分类, 这个过程重复三次, 得到的误差率分别为: 1.23%、 1.42%、 1.89%。 预测浓度和实际浓度的误差率较小, 说明达到或超过饱和厚度的水包油乳化液的荧光光谱对浓度具有较好的鉴别能力。

如果在筛选前面的数据时, 去除那些接近或达到饱和厚度的数据, 保留那些距离饱和厚度较远的数据(s> 10^-5)。 使用这些训练数据对神经网络进行训练之后, 统计出神经网络对测试数据计算输出的浓度与目标输出的差值。 训练之后使用测试数据进行分类, 这个过程重复三次, 得到的误差率分别为: 66.04%、 67.67%、 64.59%。 这样大的误差率说明未达到饱和厚度的水包油乳化液的荧光光谱对浓度的鉴别能力较差。

根据上面的实验数据可以得出结论: 不同浓度的水包油乳化液, 只要达到或超过饱和厚度, 其荧光光谱就具有较好的鉴别能力, 可以用来区分不同浓度的水包油乳化液。

如果可以根据光谱准确计算出饱和因子s, 那么可以确定此水包油乳化液是否达到饱和厚度。

继续使用图3所示的神经网络结构。 不同之处在于, 之前的神经网络的输出层神经元的输出值表示浓度, 而此处的输出层神经元的输出值表示1-s。 这里不直接输出s的原因是饱和因子可能接近0导致算出的误差率为无穷大。

神经网络的训练数据使用一系列厚度{0.05, 0.06, 0.07, 0.09, 0.1, 0.15, 0.2, 0.3, 0.5, 0.6, 0.7, 0.9, 1.0, 1.1, 1.3, 1.4, 1.5, 1.7, 1.8, 1.9 m}和浓度{1× 10^-6, 5× 10^-6, 10× 10^-6, 50× 10^-6}组合条件下的$\widetilde{K}$数据为神经网络的输入, 这些数据对应的真实饱和因子作为神经网络的目标输出。 测试使用厚度{0.08, 0.4, 0.8, 1.2, 1.6 m}和浓度{2× 10^-6, 3× 10^-6, 4× 10^-6, 20× 10^-6}组合条件下的$\widetilde{K}$数据为神经网络的输入, 这些数据对应的真实饱和因子作为神经网络的目标输出。

使用这些训练数据对神经网络进行训练之后, 统计出神经网络对测试数据计算输出的饱和因子与目标输出(即真实饱和因子)的差值。 训练之后使用测试数据进行分类, 这个过程重复三次, 得到的误差率分别为: 0.19%, 0.52%, 0.60%。

虽然误差率较小, 但是不足以准确判断乳化液是否达到饱和厚度。 这是因为在饱和因子小于10^-9时乳化液达到饱和厚度, 而10^-9比神经网络计算的误差值小得多。 然而对于那些饱和因子比较大的样本, 神经网络计算结果的准确率足以说明此乳化液未达到饱和厚度。