2022年12月, 在辽宁省大连市大连海事大学校内空地模拟油污染海冰反射光谱多角度观测实验, 为了减少外界因素反射太阳光对实验结果造成干扰, 参与本研究的成员需身着深色服装, 实验场景在户外晴朗天气下进行, 为保证试验数据的准确性, 选择在晴朗无云的中午前后进行。

反射光谱测量仪器采用ASD FieldSpec3地物光谱仪, 光谱范围为350~2 500 nm, 采样间隔为1.4 nm(350~1 000 nm)和2 nm(1 000~2 500 nm)。 考虑到试验布油, 观测及回收的可操作性, 本研究选取深约30 cm、 长50 cm、 宽40 cm的硬质塑料箱作为围油设备。 箱子内壁涂有哑光漆, 以减少内壁反光对反射率数据测量造成的影响。 其中多角度观测架由支架、 转轴、 传动杆和波谱仪探头支架杆组成, 传动杆可以以转轴为中心, 支架立面沿平面旋转, 从而达到改变观测天顶角的目的; 实验装置如图1所示。 在试验进行之初, 在半圆形转轴里面标记好角度, 保证在观测过程中, 能够以稳定的观测角度观测目标。 每间隔10°采集一次数据, 共设11个观测天顶角: -50°、 -40°、 -30°、 -20°、 -10°、 0°、 10°、 20°、 30°、 40°、 50°。 地物光谱仪采用光纤传输信号, 采用枪型探头对准观测目标, 其中光前探头的视场角为8°, 溢油充满整个视场。 为避免移动观测物标, 在转动试验容器过程中对研究场景造成破坏, 仅对采集装置的位置进行调整。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 实验概念图Fig.1 Experimental concept diagram

数据采集前, 仪器自动进行暗电流校正, 测量过程中每隔3~5 mins进行一次优化, 测量时探头距观测表面30 cm垂直向下; 参考板采用与ASD FieldSpec3配套的漫反射标准参考板, 每十次数据平均后生成一次有效数据并重复10次, 剔除异常曲线后得到反射亮度平均值DN_obj(λ); 在前后准同步测量参考板反射太阳辐射的平均值DN_ref(λ)。 通过比值法计算测量目标的反射率^[11]

Robj=DNobj(λ)DNref(λ)×Rref(1)

式(1)中, R_obj、 R_ref分别为海冰或者污染海冰和参考板的反射率; DN_obj、 DN_ref分别为海冰或者污染海冰和参考板反射亮度的平均值; λ为波谱采样点的中心波长。

在进行试验过程中, 首先将观测架立面正对着太阳入射方向即入射平面与主平面垂直, 通过旋转转动杆来调整波谱仪的观测天顶角从而获得相对方位角90°及270°的反射光谱, 后将支架旋转90°让入射平面与立面平行, 采取同样的方法, 获得相对方位角0°及180°的采样间隔数据, 这样就获得了一组冰面物标在主平面、 垂直主平面多角度的反射光谱数据。 试验结束后, 需要对溢油进行清理, 此次试验所用油量较小, 直接使用吸油毡对油污进行回收。

特征提取是光谱数据挖掘中的重要的一部分, 它可以针对光谱测量反射率数据中的有效成分进行操作, 并提取出有效数据。 特征波段的提取与后续光谱数据处理的质量与准确程度有着密切的关系, 选用光谱标准偏差特征分析方法处理数据以提取特征波段。

由于同一地物在不同观测角度下具有相似的光谱特征, 很难直接从原始光谱中选取特征波段。 故首先采用包络线去除法获取可分性光谱范围, 后利用光谱标准偏差特征分析方法处理。 光谱标准偏差特征分析方法是基于原始测量光谱数据的波段选择方法, 通过给定的准则对光谱曲线选择, 根据在光谱波长λ处, 海冰i与溢油j的光谱反射率差值的绝对值|σλ, i, j¯|大于两种观测物标在波段λ处的光谱反射率标准偏差S_{λ, i}和S_{λ, j}之和

$\begin{array}{ccc}|&\sigma_{\lambda,i,j}&|&(S_{\lambda,j}+S_{\lambda,i})\end{array}$(2)

在满足这种情况下, 我们就可以认为两种地物在波长λ处能够根据光谱曲线对其进行区分, 波长λ就是区分两种地物的高光谱特征波段, 选取适当的核驱动模型函数对光谱数据进行拟合。

地物在各个方向的反射率具有差异性, 描述地物反射率并不能简单用单一方向上的反射率来表述。 对非朗伯体而言, 它对太阳的短波辐射的反射不仅随波长而变, 也同样随着空间特征如观测角度、 方位角改变。 BRDF可以完整地描述一个表面的方向性反射率特性, 且与入射辐射亮度的空间分布函数有着稳定的函数关系。 BRDF被广泛的用于多角度遥感中, 但在实际测量上困难较大, 通常采用测量二向性反射因子(BRF)来代替BRDF的测量。 在观测视场足够小的情况下, BRF在数值上等于BRDF的π倍^[12]

R(θs, θv, φ, λ)=πf(θs, θv, φ, λ)(3)

多角度反射光谱观测数据采用基于植被辐射传输模型推导得出的体散射核与几何光学和的线性加权进行重建和拟合^[4]

R(θs, θv, φ, λ)=fiso(λ)+fvol(λ)Kvol(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ)(4)

式(4)中, R(θ_s, θ_v, φ , λ)代表在太阳天顶角θ_s、 观测方位角θ_v、 相对方位角为φ 、 波长为λ下的二向反射因子(BRF), K_vol(θ_s, θ_v, φ )以及K_geo(θ_s, θ_v, φ )分别为体散射核和几何光学核, 核系数f_iso(λ)、 f_vol(λ)、 f_geo(λ)为各向同性散射, 体散射核以及几何光学散射核函数三部分所占的权重, 即各项核系数, 最初拟合的体散射核函数为Ross Thick(罗斯厚层)核[式(5)], 几何光学核函数为Roujean核[式(6)]

Kvol(θs, θv, φ, λ)=(π/2-ξ)cosξ+sinξcosθs+cosθv-π4(5)

Kgeo=12π[(π-φ)cosφ+sinφ]tanθstanθv-1π[tanθs+tanθv+Δ(θs, θv, φ)](6)

ξ=arccos(cosθscosθv+sinθssinθssinθvcosφ)(7)

Δ(θs, θv, φ)=tan2θstan2θv+2tanθstanθvcosφ(8)

式中, ξ 为散射相角, Δ(θ_s, θ_v, φ )量化了太阳和视图方向之间的水平距离。 通过计算确定了体散射核和几何光学核。 根据多角度反射率数据, 利用最小二乘法反演出最优的3个权重系数f_iso(λ)、 f_vol(λ)、 f_geo(λ), 然后利用3个权重系数计算任意入射方向和观测角度的反射率。

传统的线性核驱动模型多是在植被基础之上建立的地表辐射传输模型, 而在冰雪覆盖的表面具有前向散射强的特征, 这是传统核驱动模型难以描述的。 因此基于瞿瑛等^[10]所引入前向散射核函数的基础上, 构建新的组合模型对冰面反射光谱进行拟合, 构建的传统线性核驱动模型拓展为以下形式[式 (9)]

R(θs, θv, φ, λ)=fiso(λ)+fvol(λ)Kvol(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ)+ffwk(λ)Kfwk(θs, θv, φ)(9)

式(9)中, K_fwk(θ_s, θ_v, φ )为前向散射核函数, 海冰表面散射相函数存在前向散射较强的特点, 且由于冰面吸收入射辐射较少, 入射光多次反射明显时, 就形成了海冰表面前向散射优势的反射特征。 本研究所选用的RPV辐射传输模型^[10]中将k和g两个参数的取值调整为前向散射占优的典型值, 忽略热点的影响, 并取固定值, g=0.066 7, k=0.846, 便得到修正之后的RPV核函数(r-RPV) [式(10)], 并作为前向散射参数核增加到原有的线性核驱动模型之中。

Kfwd=cosk-1θscosk-1θv(cosθs+cosθv)1-k1-g2(1-g2-2gcos(π-ζ))1.5+1+g21+k(1-g)2(10)

式(10)中, θ_s, θ_v, φ 分别为太阳天顶角、 观测天顶角和相对方位角。

为了比较多个线性核驱动模型对冰面反射各向异性的拟合效果, 采用传统半经验的线性核驱动模型对采集数据进行拟合分析, 各个线性核驱动拟合模型见表1, 其中半经验核函数方法有Ross Thick-Li Sparse、 Ross Thick-Li Sparse R、 Ross Thick(QU)-Roujean、 Ross Thick(QU)-Li Sparse R-r-RPV, 和本研究构建的核函数组合Ross Thick-Roujean-r-RPV。

表1

Table 1

表1(Table 1)

表1 海冰表面BRDF拟合方法 Table 1 Fitting method of sea ice surface bidirectional reflection factor Name Method Reference Ross Thick-Li Sparse R(θs, θv, φ, λ)=fiso(λ)+fvol(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ) [13] Ross Thick(QU)-Roujean R(θs, θv, φ, λ)=k0+k1fvol(λ)+k2fgeo(λ) [14] Ross Thick-Li Sparse S R(θs, θv, φ, λ)=fiso(λ)+fvol(λ)Kvol(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ) [5] Ross Thick(QU)-Li Sparse R-r-RPV R(θs, θv, φ, λ)=fiso(λ)+fvol(λ)Kvol(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ)+ffwk(λ)Kfwk(θs, θv, φ) [10] RossThick-Roujean-r-RPV R(θs, θv, φ, λ)=fiso(λ)+fvol(λ)K(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ)+ffwk(λ)Kfwk(θs, θv, φ) /

表1 海冰表面BRDF拟合方法 Table 1 Fitting method of sea ice surface bidirectional reflection factor

由于光谱数据所处通道受到水蒸气的强吸收和光谱仪剪接点偏移的影响, 在1 350~1 450、 1 800~2 050以及2 300~2 500 nm波段的光谱数据出现严重偏差^[15], 对特征波段的选择意义不大, 故被删除。

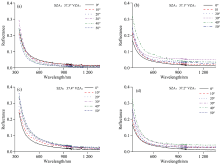
图2为清洁海冰不同方位角的反射光谱曲线, 从图像中可以了解到, 海冰的反射光谱曲线整体趋势是随着波长增加逐渐降低, 在近红外波段存在一个波峰, 在1 013~1 196 nm范围内表现为高反射。 后向光谱如图2(c), 在整个波段范围内, 反射率随观测角度的增加逐渐降低, 与图2(a)所示的前向光谱是截然相反的, 前向情况下, 随着观测角度的增加, 反射率逐渐上升。 因此在相对方位角不同时, 海冰反射率随观测角度变化的趋势不同。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 清洁海冰不同观测几何条件下反射光谱 (a): φ =0°; (b): φ =90°; (c): φ =180°; (d): φ =270°Fig.2 The reflection spectra of clean sea ice under different observation geometric conditions (a): φ =0°; (b): φ =90°; (c): φ =180°; (d): φ =270°

在主平面时如图2(b)和(d), 海冰反射曲线趋势表现为先上升后降低, 在350~1 000 nm波段区间, 在观测天顶角为40°最大随后降低。

图3是油污染海冰的不同观测几何反射光谱曲线, 从图中可以看出, 光谱曲线随观测角度变化依然存在但是变化幅度减少, 污染海冰和清洁海冰的反射率曲线相似, 整体趋势均随着波段的增大而减小, 在可见光波段下降较快, 在近红外波段反射率趋于平缓, 在单一方位角情况下, 如图3(b)和(d), 污染海冰在主平面随着观测角度的增大而增加, 在观测天顶角40°测量到最大值, 随后降低。 在垂直主平面时, 如图3(c), 前向方向时随着观测天顶角的增加而增大, 在后向方向时如图3(a), 反射率值随着观测天顶角的增加而逐渐降低。 在可见光-近红外波段可以看出受溢油污染后的海冰反射光谱并无明显特征, 与清洁海冰相比污染过后的反射率值在相同条件下有所降低, 油污染海冰的反射率值随角度变化不明显, 差异降低。 在波段1 013~1 196 nm范围内的波峰也不再明显。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 油污染海冰不同观测几何条件下反射光谱 (a): φ =0°; (b): φ =90°; (c): φ =180°; (d): φ =270°Fig.3 Reflection spectra of oil-contaminated sea ice under different observation geometry conditions (a): φ =0°; (b): φ =90°; (c): φ =180°; (d): φ =270°

海冰被油污染前后在不同观测角度下的反射光谱曲线具有相似的特征, 需要获得的特征波段即是在该波段随观测角度变化清洁海冰和油污染海冰的反射率值差异最大。 为此, 利用光谱反射率差值作为选取特征波段的方法。 光谱反射率差为海冰受污染前后采集的反射率的差值。 污染海冰反射率在可见光至1 300 nm波段低于清洁海冰。 在波长为560 nm附近反射率差值最大, 故选取560 nm波段作为特征波段进行BRDF拟合。

为了描述冰面BRDF, 利用采集的海冰受污染前后多角度反射率数据, 利用多个线性核驱动模型对其进行拟合对比分析。 实验开始时间为2022年12月, 实验所地处经纬度分别为: 121.5°E、 38.3°N; 太阳天顶角范围为36°~57.3°, 相对方位角分别选取0°、 90°、 180°和270°, 在这些方位角下, 采集多个观测角度的反射率数据。 将特征波段560 nm处反射光谱数据分别代入Ross Thick-Li sparse、 Ross Thick-Li sparse R、 RossThick(QU)-Roujean、 Ross Thick(QU)-Li sparse R-r-RPV、 Ross Thick-Roujean-r-RPV等模型中进行拟合。 将实测数据以不同形状的数据点表示, 所选用的半经验线性核驱动模型用折线形式显示其拟合结果, 拟合结果如图4所示。 图4(a)为垂直主平面中核驱动模型拟合结果, 可以观察到传统模型Ross Thick-Li Sparse R、 Ross Thick-Li Sparse、 和Ross Thick(QU)-Roujean拟合曲线偏离数据点, 不能够完整表达出海冰BRDF。 本工作构建的核驱动模型Ross Thick-Roujean-r-RPV通过绘制BRDF, 能够较好对反射特性进行拟合。 在图4(b)主平面拟合中, RossThick-Roujean模型拟合精度较差, 相比于垂直主平面, 其他各模型拟合效果相似, 更适用于主平面。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各模型拟合结果 (a): 垂直主平面; (b): 主平面Fig.4 Fitting results of each model (a): Vertical main plane; (b): Main plane

为了研究拟合数据R_fitting和实测数据R_observed的差异, 选择用差值对拟合效果进行分析。 计算公式如式(11)

Δ=|Rfitting-Robserved|(11)

将主平面和垂直主平面的差值绝对值绘制成曲线, 如图5所示。 对比图5(a)垂直主平面中各核驱动模型的差异, 其中Ross Thick-Roujean-r-RPV拟合的BRDF数据与实测数据差异最小, 差值随观测天顶角变化趋于直线, 几乎不随角度变化, 能直观表明在垂直主平面方向本文所构建模型拟合精度最高。 观察图5(b)差异数据, 各模型的拟合差值随观测角度变化上下浮动较大, 不能直观评价在该平面的拟合差异大小和拟合精度。 利用均方根误差(RMSE)对各模型在整个平面的拟合精度进行评估。 均方根误差是预测值x_i与真实值x_j偏差的平方与观测次数n比值的平方根, 用来衡量观测值同真值之间的偏差。

RMSE=(xi-xj)2/n(12)

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 拟合数据与实测数据差异 (a): 垂直主平面; (b): 主平面Fig.5 Difference between fitting data and measured data (a): Vertical main plane; (b): Main plane

不同模型的RMSE如表2所示, 在垂直主平面可以发现传统的核驱动模型Ross Thick-Li sparse R、 Ross Thick-Li sparse、 Ross Thick(QU)-Roujean 核拟合均方根误差值相近, 分别为0.025 18、 0.026 63、 0.031 74, Ross Thick(QU)-Li sparse R-r-RPV的均方根误差相对于其他传统的核函数相对较小, 本工作构建的Ross Thick-Roujean-r-RPV模型的RMSE更小, 为0.004 16, 明显低于其他传统核驱动模型, 拟合精度最高。 在主平面上, 传统模型RMSE相差较小, 本研究构建的模型依然优于其他传统模型, RMSE为0.004 62, 相比于同样引入前向散射核函数的Ross Thick(QU)- Li sparse R-r-RPV, RMSE降低了0.6%, 提高了拟合精度。

表2

Table 2

表2(Table 2)

表2 不同拟合方法的均方根误差(RMSE) Table 2 Root mean square error (RMSE) of different fitting methods Method Vertical main plane Main plane Ross Thick-Li sparse R 0.025 18 0.005 79 Ross Thick-Li sparse 0.026 63 0.005 31 Ross Thick(QU)-Roujean 0.031 74 0.011 28 Ross Thick-Roujean-r-RPV 0.004 16 0.004 62 RossThick(QU)-Li sparse R-r-RPV 0.021 29 0.004 65

表2 不同拟合方法的均方根误差(RMSE) Table 2 Root mean square error (RMSE) of different fitting methods

油污染海冰的反射吸收特征会受到观测几何的影响。 为了指导实际工作, 单一方向的BRDF图形并不能很好的描述全方位的反射特征, 利用选取的特征波段, 获得该波段油污染海冰前后在半球空间各方向反射率差值, 得到反射率差值空间分布极坐标云图, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 特征波长(560 nm)反射率差值极坐标云图Fig.6 Polar cloud map of reflectivity difference at characteristic wavelength (560 nm)

图6表明受污染前后海冰的反射率发生变化且随着观测几何的不同而存在差异。 油污染海冰前后反射率值差距较大即在特征波长表现出在该方向反射能量较大, 更能够区分出海冰是否被油污染。 从图中可以了解到在垂直主平面上受污染前后海冰反射率差值较小, 而在主平面上相对方位角250°~290°范围内, 观测天顶角50°的差值最大, 整体趋势表现出随着观测天顶角越大, 差值反射率越大, 因此在相对方位角250°~290°范围内, 较大观测角度更适合用于监测油污染海冰。