MERSI-ⅡL1B数据产品为每个反射太阳波段, 提供了一组辐射定标系数(k₀, k₁), 其中k₀为偏移量, k₁为增益系数。 利用这两个系数, 结合某个波段处的仪器观测信号值DN, 可以获得该波段处地球场景在大气层顶的表观反射率ρ_TOA

ρTOA(λ)cos(θs)d2=k1(λ)DN(λ)+k0(λ)(1)

ρTOA(λ)=[b1(λ)DN(λ)+k0(λ)]d2/cos(θs)(2)

式(1)和式(2)中, λ为MERSI的通道波长, DN为MERSI观测计数值, k₁和k₀为辐射定标系数斜率项和截距项, d和θ_s分别是MERSI观测时刻的日地距离和太阳入射天顶角。

使用相同的定标系数, 对于稳定目标上空的卫星观测, t时刻大气反射率与t₀时刻大气顶反射率的比值可反映仪器辐射响应衰减情况, 定义衰减率F如式(3)

F(λ, t)=ρTOA(λ, t)ρTOA(λ, t0)(3)

式(3)中, 若仪器的辐射响应不衰减, 对稳定目标而言, t时刻的大气顶反射率计算值与t₀时刻的计算值相等, 即F(λ, t)=1。 否则, t时刻的大气顶反射率计算值小于t₀时刻的计算值, 即F(t)<1。 因此, 需要提高定标系数补偿仪器的衰减, 使得t时刻大气辐射计算值与t₀时刻的一致, 即

ρTOA, TURE(λ, t)=ρTOA(λ, t0)(4)

将式(3)代入式(4)得到

ρTOA, TURE(λ, t)=1F(t)ρTOA(λ, t)(5)

再将式(1)和式(2)代入式(5)得到基于辐射衰减估计的辐射定标模型

ρTOA, TURE(λ, t)=1F(λ, t)(k1(λ)DN(λ, t)+k0(λ))d(t)2/cos(θs(t))(6)

式(6)中, DN(λ, t)为t时刻, MERSI波段λ观测计数值, k₀(λ), k₁(λ)为波段λ初始定标系数, 即为MERSI在轨初期的辐射定标系数。 d(t)与θ_s(t)为t时刻的日地距离因子和太阳入射天顶角。 式(6)中, 除了参数F, 其他参量DN, 初始定标系数, 太阳入射天顶角可以从仪器观测预处理后的L1数据中获得, 日地距离因子可根据仪器观测时间进行计算得到。 因此, 获得t时刻实际的大气顶反射率的关键在于获取仪器辐射衰减参量F。

参照星载光学遥感器件在太空环境中呈指数衰减假设^[9], MERSI-Ⅱ的辐射响应随时间的变化可表示为

F(λ, t)=H(λ)exp(A(λ)t)(7)

式(7)中, H和A是辐射衰减模型的系数, 本工作采用稳定目标衰减跟踪方法得到。 即, 通过遥感仪器观测稳定目标的大气顶反射率随时间的变化来推算仪器的辐射响应的变化。 这些目标主要包括亚热带沙漠、 极地冰盖和深对流云^{[10, 11, 12]}。

这里选取了国际上常用的Libya4和DCC两类稳定目标。 这两类目标各自适用于MERSI的部分反射太阳波段, 不能完全覆盖所有波段。 如DCC在海色波段容易饱和, 因为海色通道因动态范围设置小; 沙漠目标在水汽吸收波段的表观反射率随时间序列具有较大的波动性^[7]。 因此, 需要综合使用这两种目标来获取MESRI所有反射太阳波段的辐射响应衰减情况。

Libya4沙漠(28.6°N, 23.4°E)是地球观测卫星委员会(CEOS)和可见光学传感器组(IVOS)推荐的六个参考准不变定标场地(PICS)的其中之一, 具有高表面反射率(~40%)、 高空间均匀性、 良好的辐射稳定性(可见光和近红外小于2%)、 低气溶胶含量和较少的云层覆盖, 被认为是卫星发射后用于卫星光学仪器辐射定标和验证的最佳稳定目标之一^{[13, 14, 15, 16]}。

本工作选取了Libya4目标中心20×20 km²的区域, 统计出该区域的DN、 太阳角度、 卫星角度均值, 利用在轨初期的辐射定标系数, 采用式(1)和式(2)推算出研究区内的表观反射率均值, 作为Libya4目标的大气顶表观反射率。 为了确保只使用晴空的反射率来评估仪器稳定性, 采用了空间和时间均一性判据, 剔除受云污染的数据。 具体云去除判据可参考文献[6, 19]。

除了云对表观反射率大小的影响, 目标的BRDF效应也会对表观反射率的大小带来影响。 因此, 本文限制了观测天顶角VZA<20°来最小化BRDF效应。 针对云去除和卫星观测角度控制后的表观反射率时间序列, 利用式(3), 可以得到Libya4场景上的表观反射率比值时间序列F(t)

FLibya4(λ, t)=ρTOA, Libya4(λ, t)ρTOA, Libya4(λ, t0) =HLibya4(λ)·exp(ALibya4(λ)t)(8)

式(8)中, F_Libya4表示基于Libya4目标获取的仪器辐射响应衰减因子。 H_Libya4(λ)和A_Libya4(λ)表示基于Libya4目标获得的波段λ处的辐射响应衰减模型系数, 对Libya4的表观反射率比值时间序列, 使用最小二乘拟合法得到。

深对流云(DCC)是位于热带地区对流层顶部的伪不变目标, 受到水蒸气和气溶胶的影响最小, 同时也是最亮的地球稳定目标, 在可见波长上具有较高的信噪比^[20]。 DCC被广泛用于监测卫星光学遥感仪器在轨辐射响应稳定性, 如热带降雨测量任务卫星TRMM上的CERES, Aqua和Terra卫星上的MODIS, NPP和J1卫星上的VIIRS^{[17, 18]}, 以及FY-3A卫星上的MERSI^[12]。

在DCC事件发生的频率最高的热带西太平洋区域(TWP: 120°E—160°E, 20°N—20°S)进行 DCC目标像元的识别。 首先, 针对MERSI在TWP区域的观测数据, 使用11 μm亮度温度(BT)小于205.0°K实现DCC目标像元的初步识别。 其次, 为了避免DCC边缘部分、 薄云和小尺度对流单体的影响, 利用以下空间标准差滤波器对识别出的DCC目标像元进行过滤, 筛选出满足σ _BT(11 μm)<1.0°K和σ _ρ(0.65 μm)<3%的像元, 其中σ _BT(11 μm)和σ _ρ(0.65 μm)分别为11和0.65 μm波段, DCC目标像元周围3×3像素区域的标准差。 再次, 为了更多的利用DCC反射率近似朗伯体特性, 对筛选出的DCC目标像元利用SZA<40°, VZA<40°, 10°<RAA<170°进行进一步过滤, 并利用Hu等^[21]提出的DCC反射率角分布模型(ADM)对过滤后的DCC反射率进行各向异性校正[式(9)], 将所有的DCC反射率归一化到一组相同的观测几何条件下。 最后, 对归一化后的DCC反射序列, 计算每月的概率分布函数(PDFs)(图1), 统计出DCC月度返射率PDF众数, 并使用DCC月度反射率PDF众数进行MERSI辐射响应稳定性的跟踪。

RTOA, DCC(λ)=ρTOA, DCC(λ)ADM(SZA, VZA, RAA)(9)

式(9)中, ρ_{TOA, DCC}是DCC场景上的表观反射率, 使用MERSI-Ⅱ在轨初期的辐射定标系数, 结合MERSI-Ⅱ观测DN值, 利用式(1)和式(2)计算得到。 SZA, VZA和RAA分别是MERSI-Ⅱ观测DCC时对应的太阳天顶角、 观测天顶角和相对方位角。

图1

Fig.1

	Figure Option ViewDownloadNew Window
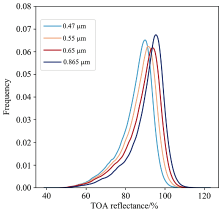	图1 2021年12月FY-3D/MERSI通道1—4 DCC大气层顶反射率PDFFig.1 DCC top reflectance PDF of FY-3D/MERSI Band 1—4 in December 2021

基于DCC月度反射率众数时间序列, 获取MERSI的辐射响应衰减模型系数过程与Libya4方法类似, 首先利用式(3)建立DCC月度反射率众数的比值序列, 然后使用最小二乘拟合法得到辐射响应衰减模型模型参数A和H

FDCC(λ, t)=RTOA, Libya4(λ, t)(RTOA, Libya4(λ, t0)=HDCC(λ)exp(ADCC(λ)t) (10)

式(10)中, F_DCC表示基于DCC目标获取的仪器辐射响应衰减因子。 H_DCC(λ)和A_DCC(λ)表示基于DCC目标获得的波段λ处的辐射响应衰减模型系数。

基于Libya4和DCC建立仪器辐射响应衰减模型, 可计算时间t₁到时间t₂期间(t₂>t₁), 仪器的总衰减率(%)和年衰减率(%)

Dtotal, PICS=F̂PICS(t2)-F̂PICS(t1)F̂PICS(t1)×100(11)

Dannual, PICS=Dtotal, PICSt2-t1×365×100(12)

式(11)和式(12)中, D_{total, PICS}和D_{annual, PICS}分别是使用Libya4或DCC方法获得的MERSI辐射响应的总衰减率和年衰减率, 单位为%,F̂PICS(t₂)和F̂PICS(t₁)分别是t₂和t₁时刻, DCC或Libya4稳定目标建立的辐射衰减跟踪监测模型计算值。

为了得到最佳的衰减率估计, 采用逆方差加权平均方法, 综合Libya4和DCC方法计算结果, 得到MERSI最终的辐射响应衰减率

Dtotal, comb=∑wiDtotal, i(13)

Dannual, comb=∑wiDannual, i(14)

wi=1/CVi∑1/CVi(15)

式(13)—式(15)中, w_i为目标i的权重系数, 由目标反射率比值时间序列的波动性大小计算得到。 这里使用变异系数(也被称为离散系数)(coefficient of variation, CV)来衡量时间序列的波动性, CV由时间序列的标准差与时间序列的均值比值计算得到。

类似的, 根据式(6), 式(8)和式(10)可以得到t时刻, 基于Libya4方法、 DCC方法及综合两种方法的MERSI的辐射定标系数

kPICS(t)=F̂PICS(t)k(t0)(16)

kcomb(t)=∑wiki(t)(17)

式(16)和式(17)中, k_PICS(t)是基于Libya4方法或DCC方法计算得到的t时刻MERSI辐射定标系数, 包括斜率和截距。 K(t₀)是MERSI初始时刻的辐射定标系数。 K_comb(t)是综合两种方法获得的t时刻MERSI辐射定标系数。 W_i为权重系数, 计算方法见式(15)。

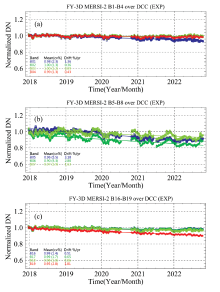
图2和图3分别展示的自2017年12月到2022年9月, 在Libya4与DCC目标上空, FY-3D MERSI-Ⅱ长时间序列的表观反射率比值, 以及辐射响应衰减模型F(t)拟合线。 F(t) 模型参数A和H列在表1中。 由于DCC在反射太阳波段的反射率较高(>80%), 而MERSI-Ⅱ的通道8—15为海色波段, 最大反射率动态范围为30%, 观测高亮度的DCC目标时, 这些波段会饱和, 所以对于海色通道采用Libya4方的结果。 但是, 海色通道在Libya4目标上空的大部分时间的观测也会饱和, 仅在冬季太阳天顶角较大时, 存在有效观测。 对于海色波段, 后期可以考虑使用低亮度的月球目标(反射率<10%)进行辐射响应衰减跟踪的研究, 以获得更为可靠的结果。 需要说明的是, 对于通道15, Libya4方法仅有两个有效观测, 因为对于通道8—15这些海色通道, Libya4方法的可信度较低, 不予以考虑。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 2017年12月—2022年9月MERSI-Ⅱ在Libya4上空的大气顶反射率时间序列及其辐射响应衰减估计 (a): 通道1—4; (b): 通道5—7; (c): 通道8—11; (d): 通道12—15; (e): 通道16—19Fig.2 Time series of reflectance of the atmospheric top of MERSI-Ⅱover Libya4 and the drift estimation in its radiometric response from December 2017 to September 2022 (a): Bands 1—4; (b): Bands 5—7; (c): Bands 8—11; (d): Bands 12—15; (e): Bands 16—19

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 2017年12月—2022年9月MERSI-Ⅱ在DCC上空的大气顶反射率时间序列及其辐射响应衰减估计 (a): 通道1—4; (b): 通道5—7; (c): 通道16—19Fig.3 Time series of reflectance of the atmospheric top of MERSI-Ⅱover DCC and the drift estimation in its radiometric response from December 2017 to September 2022 (a): Bands 1—4; (b): Bands 5—7; (c): Bands 16—19

表1

Table 1

表1(Table 1)

表1 辐射响应衰减模型参数 Table 1 Parameters of radiometric response degradation model CH CW A H CH CW A H L4 DCC L4 DCC L4 DCC L4 DCC 1 0.47 -4.78×10-5 -3.85×10-5 0.996 1.011 11 0.555 -5.75×10-6 - 1.011 - 2 0.55 -1.31×10-5 -9.92×10-6 1.002 1.006 12 0.67 2.56×10-6 -0.982 - 3 0.65 1.02×10-6 -2.45×10-6 1.002 1.000 13 0.709 1.28×10-5 - 0.990 - 4 0.865 -1.30×10-5 -1.20×10-5 1.008 1.003 14 0.746 5.90×10-8 - 0.981 - 5 1.38 - 9.45×10-5 - 1.044 15 0.865 - - - - 6 1.64 -7.89×10-5 -8.25×10-5 1.022 0.970 16 0.905 -6.32×10-6 -1.43×10-5 0.930 0.999 7 2.13 -4.57×10-5 -4.65×10-5 1.081 1.013 17 0.936 -1.64×10-5 -1.79×10-5 1.163 1.005 8 0.412 1.32×10-4 - 0.995 - 18 0.94 -2.90×10-5 -2.39×10-5 1.138 1.003 9 0.443 -6.74×10-5 - 0.991 - 19 1.03 -5.75×10-5 -5.20×10-5 1.000 0.994 10 0.49 -2.79×10-5 - 0.997 -

表1 辐射响应衰减模型参数 Table 1 Parameters of radiometric response degradation model

两个方法的时间序列波动性大小(表2中的CV值)表明, 对于水汽吸收波段(通道16—18), Libya4方法的波动性明显大于DCC方法。 如, 940 nm附近的强水汽吸收波段(通道17—18), Libya4方法的CV值约为DCC方法的10倍。 这与沙漠目标位于地球表面, 大气顶反射率会受到地表的水汽影响有关。 而DCC目标位于对流层顶部, 其反射率受大气中的水汽和气溶胶吸收影响非常小, 因此DCC更加适合用于水汽吸收光谱波段辐射性能分析, 这也是本研究为何需要综合使用多种目标的原因。 通道5(1.38 μm)是卷云波段, 大部分的能量基本被云所吸收, 无法到达地面, 所以对于该通道Libya4的有效观测仅有两个, 结果的可信度较低, 该通道也使用DCC方法的结果。 综上所述, 对于海色波段(通道8—15单独使用Libya4方法的结果, 而对于水汽吸收波段(通道16—18)和卷云波段(通道5), 单独使用DCC方法的结果。 对于其他波段, 采用1.4节所述的方法, 综合使用Libya4和DCC两种方法的结果。 各个波段的辐射衰减率计算结果列于表2中。 由表2可以看出, 两个方法计算的年衰减率具有较好的一致性, 除了通道7的差异约为1%外, 其他通道的差异在0.5%以内。

表2

Table 2

表2(Table 2)

表2 FY-3D MERSI-Ⅱ反射太阳波段辐射衰减率* Table 2 Radiometric degradation rate in reflective solar bands of FY-3D MERSI-Ⅱ CH Annual Drift/% CV/% Diff/% Annual Drift/% CH Annual Drift/% CV/% Diff/% Annual Drift/% L4 DCC L4 DCC combine L4 DCC L4 DCC combine 1 1.68 1.36 4.5 2.3 0.32 1.47 11 0.21 - 2.4 - - 0.21 2 0.47 0.36 3.0 1.3 0.11 0.39 12 -0.09 - 1.9 - - -0.09 3 -0.04 0.09 2.4 1.2 -0.13 0.05 13 -0.47 - 2.2 - - -0.47 4 0.47 0.43 2.3 1.3 0.04 0.44 14 0 - 1.8 - - 0.0 5 - 3.18 - 5.5 - 3.18 15 -1.68 - 1.3 - - - 6 2.69 2.80 4.9 5.3 -0.11 2.74 16 0.23 0.51 6.1 1.4 -0.28 0.51 7 1.60 2.63 4.4 3.9 -1.03 2.15 17 0.59 0.65 15.1 1.7 -0.06 0.65 8 4.3 - 7.9 - - 4.30 18 1.03 0.86 11.9 1.8 0.17 0.86 9 2.32 - 5.3 - - 2.32 19 2.0 1.81 3.3 2.8 0.19 1.90 10 0.99 - 3.5 - - 0.99 注: * 水汽吸收波段(通道16—18)及卷云波段采用DCC方法的结果; 海色波段(通道8—15)采用Libya4的结果; 其他波段综合使用两种方法的结果。 由于通道15Libya4的有效观测仅有2个, 衰减结果可信度不高。 Note: The data is obtained by using DCC method for water vapor absorption bands (channel 16 to 18) and cirrus band (channel 5); Libya4 method is used for ocean color channels (8~15); The combination of DCC and Libya4 is applied to remaining channels. The data is not very reliable in channel 15 sinca only two observations are obtained over Libya4.

表2 FY-3D MERSI-Ⅱ反射太阳波段辐射衰减率* Table 2 Radiometric degradation rate in reflective solar bands of FY-3D MERSI-Ⅱ

以年衰减率1%作为仪器辐射响应是否存在明显衰减的参考阈值。 选用年衰减1%作为参考阈值的原因是, 国际上MODIS和VIIRS辐射定标稳定的仪器, 年衰减率一般低于1%^{[18, 22, 23, 24]}。 根据表2中列出的各个通道衰减率结果, 可以发现年衰减率超过1%的通道主要有7个, 分别是通道1(470 nm), 通道5—7(1 380~2 130 nm), 通道8—9(412~443 nm)以及通道19(1 030 nm), 接近1%的有1个, 即通道10(490 nm)。 这些具有明显衰减的通道主要是<500 nm的蓝光波段, 1 000~2 100 nm的近红外与短波红外波段。 波长500~1 000 nm波段基本没有明显的衰减, 年衰减低基本于0.5%。 对于具有明显衰减的7个通道, 其衰减率大小与波长存在一定的关系。 具体而言, 对于波长<500 nm的3个通道, MERSI-Ⅱ的辐射响应变化与波长大小呈负相关的关系, 即, 波长最短的通道8(412 nm)衰减率最大, 年衰减为4.3%; 波长相对较长的通道1(470 nm), 年衰减最低为1.47%; 波长介于两者之间的通道9(443 nm), 衰减率介于两者之间, 为2.32%/年。 对于波长>1 100 nm的3个短波红外波段(通道5—7), 衰减率与波长大小也呈现负相关的关系。 即, 衰减最大的为通道5(1 380 nm), 年衰减率为3.18%; 其次是通道6 (1 640 nm), 衰减最小的是波长相对较长的通道7(2 030 nm), 年衰减为2.15%。

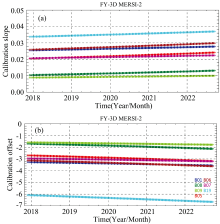
MERSI-Ⅱ自2017年11月在轨至今, 仅在2019年1月份进行了业务辐射定标系数更新, 距今已有四年。 对于存在明显衰减的通道, 长时间不更新其辐射定标系数, 其辐射定标精度难以保持在5%的指标要求范围内, 影响着后续地表、 大气等二级产品的精度及定量化应用水平。 本研究对2.1节中发现的7个具有明显衰减的通道, 使用1.4节的方法计算了其在轨至今的逐日辐射定标系数, 结果如图4所示, 定标系数斜率k₁随时间逐渐增大, k₁增大的幅度越大, 对应辐射响应衰减越大。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 重新计算的2017年12月—2022年9月FY-3D MERSI辐射定标系数斜率k1(a)及辐射定标系数截距k0(b) 加号为逐日值, 圆圈为月均值Fig.4 The recalculated FY-3D MERSI radiometric calibration slope k1 (a) and radiometric calibration intercept k0 (b) from December 2017 to September 2022 The “+”represents the daily value and the circle is the monthly mean

2.3.1 L1级产品精度

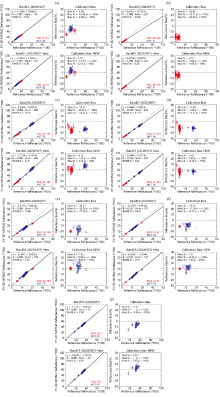
定标精度验证采用了综合检验方法^[7], 该方法融合SNO(MODIS)、 多场地(沙漠、 海洋)样本进行定标精度检验。 验证时间从2022年8月1日—2022年9月30日。 其中, SNO选取当天的交叉匹配样本, 多场地采用当天往前30天的样本。 图5给出了9月27日的定标验证结果(通道5在该天没有验证结果, 给出了9月17日的验证结果)。 从图5可以看出, 业务定标结果偏低, 其中通道5和通道8偏离1: 1线的程度最为明显, 即定标偏差最大。 使用新定标系数后, 定标验证样本拟合线较业务验证的拟合线有所提升, 更接近1∶1线。 具体定标精度见定标偏差图(图名为Calibration Bias)中rbias的统计值。 通道5的辐射定标偏差由-20.42%(业务定标)降低至-4.51%(新定标), 通道8由-18.79%降低至1.99%。 对于其他通道, 新定标系数的定标偏差较之业务定标偏差低, 基本在± 5%以内。

图5

Fig.5

Figure Option ViewDownloadNew Window

图5 2022年9月27日综合定标验证示意图 (a): 通道1; (b): 通道5; (c): 通道6; (d): 通道7; (e): 通道8; (f): 通道9; (g): 通道19 每个通道的结果图中由四个图组成; 上半边为业务验证结果, 下半边为新定标系数验证结果; 左边为定标验证散点图, 右边为定标偏差统计图; 红色点为交叉定标验证样本, 蓝色点为多场地验证样本Fig.5 Comprehensive calibration validation results on September 27, 2022 (a): Band 1; (b): Band 5; (c): Band 6; (d): Band 7; (e): Band 8; (f): Band 9; (g): Band 19 The resulting graph for each band consists of four graphs. The upper two graphs are the operational validation result, and the lower two are the new calibration coefficient validation result. The scatterplot of calibration verification is on the left, and the statistical plot of calibration deviation is on the right. The red dots are SNO samples, and the blue dots are multi-site validation samples

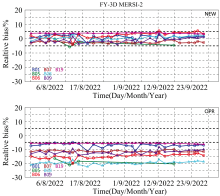
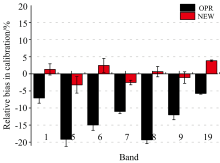
2022年8月—9月所有时间的验证结果如图6所示。 在两个月的时间内, 业务定标偏差与新定标系数的定标偏差随时间变化较平缓。 7个具有明显衰减的通道, 业务定标偏差超过了± 5%的范围, 其中通道5和8偏差最大, 约为-20%; 使用新定标系数后, 定标偏差在± 5%的范围内。 辐射衰减最大的通道8, 业务定标偏差最大, 为-19.3%; 其次是衰减仅次于通道8的短波红外波段——通道5, 为-16.6%; 对于衰减相对较小的通道19和通道1, 其业务定标误差也超过± 5%的定标精度要求。 使用新定标系数后, 这7个通道的定标精度明显提升, 通道5—7, 19的定标偏差绝对值降低到2%~4%, 其他3个通道降低到2%以内(图7)。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 2022年8月1日—2022年9月30日新的辐射定标系数(a)及业务辐射定标系数(b)对应的定标精度时间序列Fig.6 Time series of calibration accuracy corresponding to new radiometric calibration coefficient (NEW) and operational radiometric calibration coefficient (OPR) from August 1, 2022 to September 30, 2022

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 基于综合检验获取的2022年8月—9月业务和新定标系数的定标精度均值 误差线为标准差Fig.7 Average calibration accuracy of operational and new calibration coefficients for August—September 2022 obtained from comprehensive validation method The error line is standard deviation

为了检验辐射定标方法在更长时间尺度上的辐射定标精度稳定性, 这里以CEOS推荐使用的另外一个沙漠稳定目标Mauritania2(20.85N, 8.78W)为例^[15], 对采用业务定标系数以及新定标系数计算的该目标上方大气顶反射率的精度进行对比。 图8左半栏给出的是2018年1月—2022年9月该目标上空, 衰减比较大的两个蓝光波段(通道8—9)的大气顶反射率计算结果。 可以看出, 采用业务定标系数计算的大气顶反射率(图中蓝色的点)随时间存在减小的趋势, 衰减率最大的通道8尤为明显。 而使用新定标系数计算的大气顶反射率(图中红色的点)则表现出较好的稳定性。

图8

Fig.8

Figure Option ViewDownloadNew Window

图8 通道8和通道9在Mauritania2上空的大气顶反射率及辐射定标精度时间序列 (a), (c): 使用新定标系数及业务定标系数获得的通道8大气顶反射率; (b), (d): 基于辐射定标系数计算的大气顶反射率与6SV模拟计算的大气顶反射率的对比Fig.8 Time series of atmospheric top reflectance (left panel) and radiometric calibration accuracy (right panel) of bands 8—9 over Mauritania2 (a), (c): Atmospheric top reflectance of band 8 obtained using new calibration coefficient and operational calibration coefficient; (b), (d): Comparison between the reflectance of the atmospheric top calculated using the radiometric calibration coefficient and the reflectance calculated from the 6SV simulation

图8右半栏是以辐射传输模式6sv模拟计算的大气顶反射率为验证参考, 对采用不同的辐射定标系数计算的大气顶反射率进行精度验证。 从精度验证结果可以看出, 通道8与通道9的业务定标精度呈明显的逐渐下降的趋势, 并且分别从2019年下半年和2019年底, 两者的定标精度已经超过了± 5%的要求, 到2022年9月份, 两者的辐射定标误差分别接近-18%和-10%。 而使用新定标系数计算的结果则表现出较好的稳定性和精度, 通道8和通道9的辐射定标误差时间序列标准差均在1%以内, 分别保持在2.65%± 0.9%(均值± 标准差)和0.83%± 0.9%附近。 由此可见, 本研究的提出的辐射定标方法对维持辐射定标精度的长时间稳定性具有一定的优势, 从而确保后续地表、 大气等二级产品的定量化应用效果。

2.3.2 L2级产品精度改进效果验证

这里以MERSI-Ⅱ的L2级为例说明本研究的方法对辐射定标精度的提升情况, 包括气溶胶光学厚度和海色产品两类产品。 气溶胶光学厚度产品的获取需要输入通道1(470 nm), 通道3(650 nm)和通道7(2 130 nm)的L1级产品数据。 气溶胶光学厚度反演算法中, 地表反射率的估计是气溶胶反演至关重要的一步, 是影响气溶胶反演精度的主要因素之一。 根据短波红外2.1 μm波段受气溶胶影响较小的假设, 由通道7的L1级辐射产品数据, 利用统计的波段比值关系, 实现0.65 μm红光波段和0.47 μm蓝光波段的地表反射率的估计^[25]。 因此, 通道7的辐射定标精度对气溶胶产品精度至关重要。 MERSI-Ⅱ的海色产品采用深度学习+贝叶斯最优估计理论, 获取通道8—15的归一化离水辐亮度^[26]。

图9和图10分别给出的是定标更新前后, 气溶胶光学厚度产品和海色产品的精度验证结果。 结果显示, 定标系数更新后, 两类产品精度的提升均具有正向效果。 对于气溶胶光学厚度产品, 在定标系数更新前, 该产品存在低估问题, AOD的整体误差范围为-0.05~-0.08, 落在MODIS指标 EE 范围之外, 样本数仅为51%~65%。 但在定标系数更新后, 整体误差范围降至-0.01~0.01之间, 同时样本数显著增加, 达到了65%~82%, 落入了MODIS指标EE范围内。 对于海色产品, 通道8(412 nm)和通道9(443 nm)的定标系数更新后, 412 nm波段的MERSI-Ⅱ产品与VIIRS产品的相关系数R从0.24提升至0.78, 产品误差bias约从0.01降低至0.004。 443 nm波段的 MERSI-Ⅱ产品与VIIRS产品的相关性R从0.59提升至0.68, 产品误差bias约从0.007降低至0.003。

图9

Fig.9

Figure Option ViewDownloadNew Window

图9 定标更新前后气溶胶光学厚度产品精度对比 从左往右依次为2023年3月15日, 2023年3月16日, 2023年3月21日段产品验证结果(a): 使用业务定标系数(定标更新前); (b): 使用新定标系数(定标更新后)Fig.9 Comparison of aerosol optical thickness product accuracy before and after calibration update From left to right are the results of March 15, 2023, March 16, 2023, and March 21, 2023 (a): Using the operational calibration coefficient (before calibration update); (b): Using the new calibration coefficient (after calibration update)

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 定标更新前后412 nm(左)和443 nm(右)处离水辐射产品精度对比(20230316日产品) (a): 使用业务定标系数(定标更新前); (b): 使用新定标系数(定标更新后Fig.10 Comparison of the precision of out-of-water radiation products at 412 nm (left) and 443 nm (right) before and after calibration update (2023/03/16) (a): Using the operational calibration coefficient (before calibration update); (b): Using the new calibration coefficient (after calibration update)