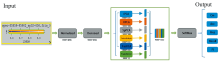
SATS是一个拥有输入层、 归一化层、 去噪层、 特征提取层和SoftMax输出层5层网络架构的算法。 SATS算法结构如图1所示。 结构图中的数字是该层输出数据的维度。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 SATS算法结构图Fig.1 SATS algorithm structure diagram

本文选用的实验数据如下: ①LAMOST-DR8数据集中r波段信噪比大于30的高质量F、 G、 K型恒星光谱, 其中F、 G、 K型恒星光谱各3000条; ②SDSS恒星光谱模板库中的F、 G、 K型恒星光谱, 其中F、 G型恒星光谱各10条, K型恒星光谱13条。 恒星光谱在不同波长位置处流量差异巨大, 在有吸收线的位置流量值往往较低。 对机器学习算法而言, 数据自身较大的差异会使算法学习到过多无用特征, 导致最终结果不佳。 对恒星光谱进行归一化处理, 使光谱流量处于同一数量级, 不仅消除了光谱自身一些较大的差异, 还使算法收敛的更快。 本文使用式(1)所示的线性归一化函数, 来对光谱做归一化处理。

Fluxn=flux-fluxminfluxmax-fluxmin(1)

式(1)中, flux为原始光谱流量, flux_max和flux_min分别为原始流量的最大值和最小值, Flux_n表示归一化后的流量。

SVD算法有较好的零相移特性和稳定性, 可以很好地抑制窄带噪声。 本文舍弃了光谱去噪领域较为流行的小波变换去噪算法, 转而使用SVD算法来对光谱做去噪处理。 详见第2.1节。 SVD去噪分三个步骤进行。 首先将恒星光谱构造为一个Henkle矩阵, 如式(2)

H=y(1)y(2)…y(L)y(2)y(3)…y(L+1)︙︙⋱︙y(N-L+1)y(N-L+2)…y(N)(2)

式(2)中, N为光谱数据个数, L为窗长度。 然后对H矩阵进行奇异值分解, 如式(3)

H=SVDT=u1σ1vT1+u2σ2vT2+…+uPσPvTP(3)

式(3)中, S为HH^T的左奇异矩阵; D为HH^T的右奇异矩阵; V是奇异值的对角矩阵。 最后, 对奇异值进行处理并重构信号。 将对应奇异值处理后, 可以得到新对角矩阵V', 设重构后的Henkle矩阵为H', 则有式(4)

H'=SV'DT(4)

对重构矩阵H'做反对角平均处理, 以实现抑制窄带噪声。

包含六个模块的特征提取层是SATS算法的核心控制层。 传统的PCA模块将全部数据一次性放入内存进行计算, 对海量高维数据来说, 这显然会降低硬件的运行效率并缩短硬件的使用寿命。 IPCA模块将海量数据分为若干小块, 每次只对其中的一块数据进行计算。 这样不仅可以用来处理更大规模的数据集, 同时也方便了在线处理。 为了更好地提取数据的“非线性”特征, 使用非线性映射将原始光谱数据投射到高维特征空间, 然后在这个高维特征空间中使用PCA, 这就是KPCA。 众所周知, 传统的PCA模块可解释性较差, SparsePCA模块即是为了解决此问题而产生的算法。 SparsePCA将主成分系数变得稀疏, 换言之, 即把部分系数变为0, 以这样一种方式将主成分的主要部分凸显出来, 这样主成分就会变得容易解释。 FastICA是近几年出现的算法, 其原理基于递推算法, 它最大的优势就是适用于各种各样的数据。 FastICA在每一次迭代中均有大量数据参与运算, 即它以批处理的形式对数据进行处理。 从并行处理的角度看, FastICA可以看作是神经网络算法, 这也就让它具有众多神经网络算法的优点: 并行的、 分布的、 计算简单、 占用内存少。 Factor Analysis是PCA的延伸和拓展应用, 其定义如式(5)

X-μ=Af+ε(5)

式(5)中, X为光谱数据, f为潜在变量, A为因子载荷, ε 是误差项。 A为X和f之间的相似性, 因子变量值越大, X和相应因子间的相似性就越高。 使用多种Analysis模块对恒星光谱进行特征提取, 自然就包含了多种计算方式下的光谱特征, 从而使原始光谱特征损失更少。

Transformer特征提取模块包含四个小模块, 连续谱拟合模块、 连续谱归一化模块、 谱线积分模块和Transformer特征学习模块。 谱线特征是LAMOST产出光谱最有效的特征, 为了获取谱线信息, 需要拟合光谱的连续谱, 本文使用7阶多项式来拟合连续谱。 连续谱归一化是剔除连续谱特征获得谱线信息的有效手段。 设拟合连续谱流量为F″, 去噪后的光谱流量为F', 则归一化后的光谱F可表示为式(6)

F=F'F″(6)

本文将整个波长区间进行10等分, 使用梯形积分法对光谱谱线信息进行数值积分。 最后每条光谱对应产生10个积分值, 这10个积分值即为恒星光谱的新特征。 最后, 使用Transformer实践应用算法BERT对10个积分值进行特征学习。 Transformer模型的计算核心是Attention函数, 其计算过程如式(7)所示

MultiHead(Q, K, V)=Concat(head1, …, headh)WQ(7)

其中, head_i=Attention(Q WiQ, K WiK, V WiV),WiQ∈Rdmodel×dk,WiK∈Rdmodel×dk,WiV∈Rdmodel×dv, W^O∈Rdmodel×hdv。

大气湍流等自然因素以及观测设备自身的一些漏洞, 导致LAMOST产出光谱掺杂了一定的噪声。 为了避免噪声对科研任务的影响, 需要对光谱做去噪处理。 小波变换是恒星光谱去噪领域最常用的方法, 但是通过本文的实验, 我们发现SVD算法更适合应用于恒星光谱的去噪任务。 因为LAMOST没有较精准的模板光谱, 所以使用SDSS恒星光谱模板库中的恒星光谱作为实验数据。 假定模板光谱不含有任何噪声, 人工为其添加高斯白噪声、 均匀白噪声和泊松噪声后, 使用小波变换和SVD算法对添加噪声后的光谱分别做去噪处理, 以去噪前后光谱的信噪比衡量去噪算法的性能。 其中, 高斯白噪声的信噪比为3 dB, 均匀白噪声的均值和方差分别为: 0, 0.1, 泊松噪声的常系数为0.1。 信噪比的计算, 如式(8)—式(10)。 在本节中, 信噪比作为一种指标, 只为衡量两种去噪算法的去噪能力, 1.2节所述信噪比来自LAMOST, 其经过了复杂的计算, 对天体光谱来说, 更科学、 更符合天体的物理化学性质, 和本节信噪比没有联系。 恒星光谱掺杂的噪声多以随机噪声的形式存在, 故本实验主要考察两种算法剔除随机噪声的能力。 实验结果如表1, 表2所示。 需要说明的是, 我们虽然指定了噪声的生成参数, 但噪声产生的随机性, 还是让恒星光谱的信噪比不尽相同。

S=∑iL|flux(i)|2L(8)

N=∑i, jL|flux(j-i)|2L(9)

SNR=10×log10SN(10)

其中, S为原始恒星光谱的功率, N为噪声功率, flux为光谱流量。

表1

Table 1

表1(Table 1)

表1 SVD去噪前后模板光谱的信噪比 Table 1 Signal to noise ratio of SVD template spectrum before and after denoising SVD 加入高斯白噪声 加入均匀白噪声 加入泊松噪声 去噪前S/N 去噪后S/N 去噪前S/N 去噪后S/N 去噪前S/N 去噪后S/N Spec_1 0.467 3 10.394 8 7.711 1 17.537 3 7.694 0 14.981 4 Spec_2 0.524 9 10.957 4 7.574 9 17.485 7 7.312 3 14.259 5 Spec_3 0.795 6 11.210 3 7.787 4 17.979 5 7.535 3 14.518 4

表1 SVD去噪前后模板光谱的信噪比 Table 1 Signal to noise ratio of SVD template spectrum before and after denoising

表2

Table 2

表2(Table 2)

表2 小波变换去噪前后模板光谱的信噪比 Table 2 Signal to noise ratio of template spectrum before and after wavelet transform denoising Wavelet 加入高斯白噪声 加入均匀白噪声 加入泊松噪声 去噪前S/N 去噪后S/N 去噪前S/N 去噪后S/N 去噪前S/N 去噪后S/N Spec_1 0.630 4 9.348 4 7.643 8 16.270 5 7.254 9 13.466 2 Spec_2 0.619 3 9.556 4 7.544 8 16.455 0 6.795 4 12.773 6 Spec_3 0.684 3 9.471 8 7.782 5 16.644 5 7.653 7 13.951 8

表2 小波变换去噪前后模板光谱的信噪比 Table 2 Signal to noise ratio of template spectrum before and after wavelet transform denoising

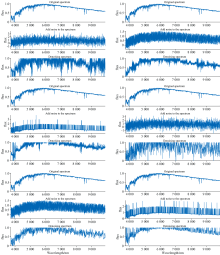
添加不同类型的噪声后, 模板光谱的信噪比出现了不同程度的变化。 由表1、 表2可以看出, SVD算法去噪后的光谱, 其信噪比更高。 对于添加高斯白噪声的光谱, 小波变换为其去噪后, 光谱的信噪比不到10, 而SVD超过10; 对于添加均匀白噪声的光谱, 小波变换为其去噪后, 光谱的信噪比不到17, 而SVD超过17; 对于添加泊松白噪声的光谱, 小波变换为其去噪后, 光谱的信噪比不到14, 而SVD超过14。 图2为一条光谱去噪前后的展示图, 上方3图使用的是SVD算法, 下方3图使用的是Wavelet算法。 其中, 左侧图处理的是高斯噪声、 中间图处理的是均匀噪声、 右侧图处理的是泊松噪声。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 SVD和小波变换去噪前后的模板光谱图Fig.2 SVD and wavelet transform before and after denoising template spectra

从图2左侧图可以看出, SVD算法剔除高斯噪声后, 保留了恒星光谱的吸收线、 发射线结构, 而Wavelet算法将全谱范围内的谱线拉长、 “变稀”; 从图2可以看出, SVD算法虽然改变了谱线的宽度, 但是很好地凸显出了主要谱线特征, 反观Wavelet算法, 其将谱线处理的过于稀疏, 让恒星光谱在全谱范围内保持了某种波动规律; 从图2右侧图可以看出, 由于添加噪声的扰动过大, 导致光谱蓝端出现了较大误差, 但是从全谱范围内来看, SVD算法很好地保留了光谱的发射线、 吸收线结构, 而Wavelet算法除保留了部分蓝端谱线外, 基本丢失掉了恒星光谱的吸收线和发射线结构。 基于以上论述, 我们认为SVD算法更适合用于剔除光谱的随机噪声。 由于对恒星光谱做了归一化处理, 因此, 本节仅关注[0, 1]区间内的数据, 可以肯定, 超出此区间范围的数据一定是噪声。

在上面的论述中, 我们比较了SVD、 Wavelet两种算法剔除光谱随机噪声的能力。 但是, 上面的论述只使用了一条恒星光谱进行实验, 实验结果或许有一定的随机性。 在接下来的论述中, 我们从SDSS恒星光谱模板库挑选了F、 G、 K型恒星光谱各10条进行实验。

恒星光谱去噪前后的‘ 差异性’ , 是衡量一个去噪算法性能的重要参考标准, 本次实验, 为添加噪声的恒星光谱做去噪处理后, 我们将其同原始恒星光谱进行了比较, 计算了整个波长区间内流量的绝对误差, 计算公式如式(11)。 实验结果如表3。

Error* =∑iFlux(i)-flux(i)|(11)

式(11)中, Flux为去噪后的光谱流量, flux为原始光谱流量。

表3

Table 3

表3(Table 3)

表3 SVD、 Wavelet去噪前后光谱流量的绝对误差 Table 3 Absolute error of spectral flux before and after SVD and Wavelet denoising F G K Total 1 SVD 90.145 63 114.538 1 106.355 6 311.039 3 2 87.611 01 103.087 3 108.852 2 299.550 5 3 85.745 16 101.491 5 103.402 3 290.638 9 4 90.491 53 108.358 8 99.675 86 298.526 2 5 81.236 7 105.502 9 103.742 8 290.482 4 6 88.678 43 99.318 42 103.672 7 291.669 5 7 90.212 13 107.575 3 110.059 7 307.847 2 8 84.164 09 107.395 1 114.985 3 306.544 5 9 90.562 79 99.461 35 112.934 2 302.958 3 10 85.047 9 98.089 09 108.686 9 291.823 8 11 Mean 87.389 54 104.481 8 107.236 7 299.108 1 12 Variance 10.379 27 26.542 17 22.526 59 59.448 03 13 Wavelet 112.305 5 122.716 8 117.060 5 352.082 7 14 111.788 3 113.767 2 118.138 343.693 4 15 109.477 106.585 1 117.776 4 333.838 5 16 113.500 8 118.211 9 110.495 2 342.207 9 17 106.080 4 113.858 1 118.466 2 338.404 6 18 110.118 111.437 1 118.868 3 340.423 4 19 112.196 116.636 4 121.908 9 350.741 3 20 101.889 5 121.120 2 128.351 5 351.361 2 21 114.722 4 115.952 8 125.802 1 356.477 3 22 108.522 5 107.627 6 124.777 8 340.927 8 23 Mean 110.06 114.791 3 120.164 5 345.015 8 24 Variance 14.607 73 27.905 94 26.737 82 69.251 49

表3 SVD、 Wavelet去噪前后光谱流量的绝对误差 Table 3 Absolute error of spectral flux before and after SVD and Wavelet denoising

在表3中, 1—10行是SVD算法去噪后的光谱流量同原始光谱流量的绝对误差; 13—22行是Wavelet算法去噪后的光谱流量同原始光谱流量的绝对误差。 从表3可以看出, F型恒星光谱经SVD算法处理后, 产生了10个绝对误差数据, 这10个数据的均值和方差是87.389 56和10.379 27; F型恒星光谱经Wavelet算法处理后, 产生了10个绝对误差数据, 这10个数据的均值和方差是110.06和14.607 73, 这说明, Wavelet算法处理后的恒星光谱同原始恒星光谱相比‘ 差距’ 更大, 而且稳定性不如SVD算法, 对于G、 K型恒星光谱可以得出相同的结论。 F、 G、 K型恒星光谱经SVD算法处理后, 产生了30个绝对误差数据, 这30个数据的均值和方差是299.108 1、 59.448 03, F、 G、 K型恒星光谱经Wavelet算法处理后, 产生了30个绝对误差数据, 这30个数据的均值和方差是345.015 8、 69.251 49, 这说明SVD算法去噪后的恒星光谱同原始恒星光谱相比, 差异性更小, 稳定性更高。 因此, 我们认为SVD算法更适合用于剔除光谱的随机噪声。

在2.1节中, 我们证实了SVD算法可以很好地应用于恒星光谱去噪任务, 然而对恒星光谱做去噪处理真的会提高分类正确率吗? 本节实验用来回答这个问题, 我们使用SVD去噪算法进行本次实验。 采用对比实验的形式进行本次实验: (1)将归一化处理后的F、 G、 K型恒星光谱直接输入至SoftMax层进行分类; (2)将归一化后的光谱做去噪处理后, 再输入至SoftMax层进行分类。 通过前后两次实验结果的比较, 来考察对光谱做去噪处理是否真的会提高分类正确率。 在本文中, SoftMax层的损失函数是数据集损失和正则项损失的加和。 实验结果如表4所示, 其中Ⅰ代表第一次实验, Ⅱ代表第二次实验。

表4

Table 4

表4(Table 4)

表4 去噪效果评估的实验结果 Table 4 The experimental results of denoising effect evaluation Acc Prec Recall F1 Test_acc F 0.86 0.82 0.74 0.78 Ⅰ G 0.77 0.65 0.64 0.65 0.76 K 0.9 0.81 0.91 0.86 F 0.93 0.89 0.89 0.89 Ⅱ G 0.8 0.71 0.71 0.71 0.8 K 0.87 0.81 0.81 0.81

表4 去噪效果评估的实验结果 Table 4 The experimental results of denoising effect evaluation

可以看出, 使用去噪的恒星光谱进行实验, 其实验结果的绝大数指标是更优的。 此外, 测试集分类准确率也由0.76提高至0.8。 因此得出结论: 对恒星光谱做去噪处理是必要的。

PCA作为经典的特征降维算法, 在恒星光谱降维领域已广泛应用。 IPCA、 KPCA、 SparsePCA、 FactorAnalysis和FastICA作为独立的模块, 同样可以对恒星光谱做特征降维处理。 本节实验旨在考察: 使用不同的Analysis模块对恒星光谱分类任务的影响。 本节实验的工作机制如下: IPCA、 KPCA、 SparsePCA、 FactorAnalysis和FastICA五个特征降维模块, 对SVD算法去噪后的恒星光谱分别做特征降维后, 输入到SoftMax层进行自动分类。 实验结果如表5所示。

表5

Table 5

表5(Table 5)

表5 使用单一特征提取模块进行分类的实验结果 Table 5 Experimental results of classification using a single feature extraction module Acc Prec Recall F1 Test_acc F 0.87 0.82 0.78 0.8 IPCA G 0.81 0.7 0.74 0.72 0.81 K 0.94 0.91 0.91 0.91 F 0.88 0.86 0.81 0.83 KPCA G 0.84 0.72 0.8 0.76 0.84 K 0.96 0.95 0.91 0.93 F 0.9 0.89 0.81 0.85 SparsePCA G 0.86 0.75 0.85 0.8 0.86 K 0.96 0.95 0.92 0.94 F 0.9 0.88 0.85 0.86 FactorAnalysis G 0.87 0.78 0.81 0.8 0.87 K 0.96 0.93 0.94 0.94 F 0.88 0.82 0.82 0.82 FastICA G 0.84 0.76 0.76 0.76 0.84 K 0.96 0.94 0.93 0.93

表5 使用单一特征提取模块进行分类的实验结果 Table 5 Experimental results of classification using a single feature extraction module

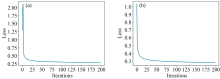
由表5可以看出, 使用FactorAnalysis模块对恒星光谱做特征提取是最有效的, 该次实验的大部分分类指标均优于其他实验。 其次是SparsePCA模块, 使用该模块对恒星光谱做特征提取后再分类, 分类正确率达到了0.86。 使用IPCA模块、 KPCA模块、 SparsePCA模块和FactorAnalysis模块进行的分类实验, 其所对应的收敛曲线如图3所示, 其中图3(a)为使用IPCA模块进行的实验, 图3(b)为使用KPCA模块进行的实验, 图3(c)为使用SparsePCA模块进行的实验, 图3(d)为使用FactorAnalysis模块进行的实验。 将特征降维后的前两个‘ 特征数据’ 作为横坐标、 纵坐标的数据分布图, 如图4所示, 其中图4(a)为使用IPCA进行实验的数据分布图, 图4(b)为使用KPCA进行实验的数据分布图, 图4(c)为使用SparsePCA进行实验的数据分布图, 图4(d)为使用FactorAnalysis进行实验的数据分布图。 图中3种颜色代表F、 K、 G三种光谱, 即用特征向量的两个特征值代表一条光谱。

图3

Fig.3

	Figure Option ViewDownloadNew Window
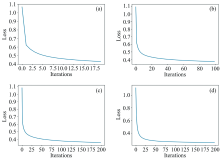	图3 使用IPCA、 KPCA、 SparsePCA、 FactorAnalysis特征提取模块进行实验的收敛曲线图Fig.3 Use IPCA, KPCA, SparsePCA, FactorAnalysis feature extraction modules to carry out the convergence diagram of the experiment

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 ‘ 特征’ 数据分布图Fig.4 ‘ Feature’ data distribution map

从2.3节可以看出, 使用单一Analysis模块, 对恒星光谱做特征降维后再分类, 其测试数据集的分类正确率已经在0.8以上。 如果将各Analysis模块结合使用, 会不会有更优的实验效果? 本节实验旨在说明这个问题。

首先将各Analysis模块进行横向组合。 即对一条4 096维的恒星光谱来说, 将使用一个1500维的新“光谱”代替。 实验结果如表6所示。

表6

Table 6

表6(Table 6)

表6 特征提取模块组合使用的实验结果 Table 6 Experimental results of the combination of feature extraction modules Acc Prec Recall F1 Test_acc Analysis模块 横向组合 F 0.96 1 0.86 0.93 G 0.92 0.87 0.88 0.87 0.91 K 0.95 0.88 0.98 0.93 Analysis模块 纵向组合 F 0.95 0.91 0.93 0.92 G 0.89 0.84 0.84 0.84 0.89 K 0.94 0.92 0.9 0.91 Analysis+ Transformer模块 横向组合 F 0.95 0.96 0.89 0.92 G 0.95 0.88 0.95 0.91 0.93 K 0.95 0.94 0.94 0.94

表6 特征提取模块组合使用的实验结果 Table 6 Experimental results of the combination of feature extraction modules

然后将各Analysis模块进行纵向组合。 即对一条4 096维的恒星光谱来说, 将使用一个300维的新“光谱”代替。 需要说明的是, 此300维的新“光谱”是各Analysis模块产出数据的加和。 实验结果如表6所示。

由表6可以看出, 将Analysis模块结合使用, 对恒星光谱分类任务是有益的。 Analysis模块横向组合、 纵向组合后, 其测试集分类正确率均高于只使用单一Analysis模块的分类正确率。 FactorAnalysis作为最优的Analysis模块, 其测试集分类正确率为0.87; 而将Analysis模块横向组合、 纵向组合后, 测试集准确率达到了0.91、 0.89。 两次实验的收敛曲线如图5所示, 其中图5(a)为Analysis模块横向组合的收敛曲线图, 图5(b)为Analysis模块纵向组合的收敛曲线图。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 Analysis模块结合使用的收敛曲线图Fig.5 Convergence graphs used in combination with analysis modules

将Analysis模块结合使用, 可以优化恒星光谱分类任务的实验效果。 本次实验, 将NLP领域大放光彩的Transformer实践应用算法‘ BERT’ 作为特征提取模块, 同Analysis模块结合使用, 来进一步优化恒星光谱分类任务的实验效果。 由2.4节可以看出, 将Analysis模块横向组合可以有更好的实验结果, 因此, 本节将Transformer模块同Analysis模块继续横向组合。 本次实验结果如表6所示。

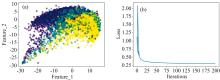
本次实验, 我们进一步提高了测试集的分类正确率, 测试集分类正确率由0.91提高至0.93, 其他实验指标也有不同程度的优化。 SATS算法由此产生。 本次实验的数据分布图和收敛曲线图如图6所示, 图中3种颜色代表F、 K、 G三种光谱, 也即用特征向量的两个特征值代表一条光谱。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 Transformer、 Analysis模块结合使用的 收敛曲线图和数据分布图Fig.6 Convergent graphs and data distribution diagrams used in combination with Transformer and Analysis modules

本节实验的工作机制如下: SVD算法对归一化恒星光谱做去噪处理后, 输入至卷积神经神经网络(CNN)^[16]中进行特征提取, 再输入至贝叶斯算法(Bayes)、 K近邻算法(KNN)、 支持向量机算法(SVM)、 Adaboost算法和随机森林算法(RF)中进行分类。 最后, 将混合深度学习算法的分类正确率, 同SATS算法的实验结果进行比较, 以此来考察SATS算法的分类性能。 实验结果如表7所示。

表7

Table 7

表7(Table 7)

表7 对比算法的分类正确率 Table 7 Classification accuracy of comparison algorithm 算法 CNN+Bayes CNN+KNN CNN+SVM CNN+Adaboost CNN+RF 分类正确率 0.86 0.88 0.89 0.87 0.89

表7 对比算法的分类正确率 Table 7 Classification accuracy of comparison algorithm

由表7可以看出, 混合深度学习算法的分类正确率最高为0.89, 低于SATS算法0.93的分类正确率。 由此也证明了SATS算法可以胜任恒星光谱分类任务, 它是有效的、 是优异的。