高分辨率罗兰圆光学系统的色差校正方法研究

引用本文

陈吉文, 陈作儿. 高分辨率罗兰圆光学系统的色差校正方法研究[J]. 光谱学与光谱分析, 2024,44(7): 2011-2017.
CHEN Ji-wen, CHEN Zuo-er. Research on Chromatic Aberration Correction Method for High-Resolution Roland Circle Optical System[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 2011-2017.
Doi:10.3964/j.issn.1000-0593(2024)07-2011-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

高分辨率罗兰圆光学系统的色差校正方法研究

陈吉文, 陈作儿

北方工业大学电气与控制工程学院, 北京 100144

作者简介: 陈吉文, 1971年生,北方工业大学电气与控制工程学院教授 e-mail: chenjiwen@ncut.edu.cn

收稿日期: 2023-07-05 修回日期: 2023-10-25

基金: 科技部重点研发计划项目(2021YFF0700102)资助

摘要

罗兰圆光学系统优点众多, 但系统中因平凸透镜的使用, 导致各特征波长色散后的成像点在罗兰圆附近产生了一定量的偏移量, 使得各波长成像点依次排列在一条曲面上。由于目前新型采集器件线阵CMOS或CCD的使用, 而这类传感器的感光面是一个平面, 因此导致结果产生较严重的色差。提出了一种使用加权最小二乘法拟合像面的色差校正方法, 并计算出系统像面的中心偏移距和偏移倾斜角这两个校正参数, 将其引入原本罗兰圆光学系统进行色差校正, 从而确定线阵光电传感器像面的最佳位置, 实现高分辨率。此外在真空紫外光谱中C、 P和S等元素非常重要, 可使用本文提出的基于加权最小二乘法的色差校正方法, 通过增加这类元素权值占比, 实现最优分辨率。最后通过Zemax软件进行光学仿真, 完成了罗兰圆光学系统的仿真以及优化。并给出170~410 nm波段点列图的成像宽度仿真以及各元素特征波长在CMOS传感器上所采集到的光谱图, 推算出其实际应用中的分辨率, 其照度光谱图显示其分辨率均可保持在0.02 nm, 接近系统理论最佳分辨率。研究结果表明基于加权最小二乘法拟合像面的方法, 可实现罗兰圆光学系统的色差校正, 实现高分辨率。

关键词: 罗兰圆光学系统; 平凸透镜; 色差校正; 高分辨率; 加权最小二乘法

中图分类号:TH744 文献标志码:A

Research on Chromatic Aberration Correction Method for High-Resolution Roland Circle Optical System

CHEN Ji-wen, CHEN Zuo-er

School of Electrical and Control Engineering, North China University of Technology, Beijing 100144, China

Abstract

The Roland circle optical system has many advantages. Still, due to using a planoconvex lens in the system, the imaging points that have undergone dispersion also generate a certain amount of offset distance near the Roland circle, resulting in the imaging points of each characteristic wavelength arranged sequentially on a curved surface. Due to the current use of new collection devices such as linear array CMOS or CCD, where the photosensitive area of these sensors is a flat surface, serious chromatic aberration is caused in the results. This article proposes a chromatic aberration correction method using the weighted least squares method to fit the image plane and calculate the two correction parameters of the center offset distance and offset tilt angle of the system image plane. Based on the original Roland circle optical system, these two correction parameters are introduced for chromatic aberration correction, thereby determining the optimal position of the linear array photoelectric sensor image plane and achieving high resolution. In addition, elements such as C, P, and S are very important in the VUV spectrum. The chromatic aberration correction method based on weighted least squares proposed in this article can achieve optimal resolution by increasing the weight proportion of characteristic wavelengths of such elements. Finally, optical simulation was conducted using Zemax software to complete the simulation and optimization of the Roland circle optical system. The imaging width simulation of spot diagrams in the 170~410 nm wavelength range and the spectral images of each element’s characteristic wavelengths collected on CMOS sensors were provided. The resolution in practical applications was calculated, and the illuminance spectral images showed that their resolution could be maintained at 0.02 nm, close to the optimal theoretical resolution of the system. The research results of this article indicate that using the weighted least squares method to fit the image plane can achieve chromatic aberration correction for Roland circle optical systems and achieve high resolution.

Keyword: Roland circle optical system; Planoconvex lens; Chromatic aberration correction; High resolution; Weighted least squares method

文章图片

引言

火花与电弧发射光谱仪的主要工作波长范围在170~410 nm, 其在钢铁冶金、有色地矿、化学化工等众多领域都有广泛的应用^[1]。目前光谱仪根据分光系统的不同可分为C-T型系统、罗兰圆系统、中阶梯系统。其中罗兰圆光学系统将凹面光栅作为色散元件, 这类光栅同时具备色散和聚焦的作用, 这使得系统具有光路简洁、光强度损失小、各特征波长在全谱范围内可实现相同的分辨率等优点。但在该光学系统中由于平凸透镜的使用, 使得各特征波长最终无法完美地成像于线阵CMOS或CCD这类传感器的平面感光面上, 从而给系统产生了较严重的色差。

分辨率是各类光学系统最主要的技术指标之一。为了实现高分辨率常规方法就是使用高刻线数和大曲率半径的光栅, 但这会导致设备的成本较高且不利于小型化。或者减小狭缝宽度提升分辨率, 然而这会减弱光通量, 从而降低设备总体的光灵敏度^[2]。本研究所设计的光学系统就是以2 400 L·mm^-1刻线密度、曲率半径为401.56 mm的全息凹面光栅作为色散元件的罗兰圆光学系统。为了满足分析行业中高分辨率的要求, 本研究提出了一种结合加权最小二乘法进行像面拟合的色差校正方法, 优化像面的相对位置与倾斜角使系统色差的影响降到最低。此外在实际检测中, 分布在170~200 nm波段范围内的C、 P和S等这类元素常作为重点检测的对象。因此需要重点优化这类元素的分辨率^{[3, 4]}。本研究所采用的加权最小二乘法拟合像面的色差校正方法可通过对目标元素波长权值占比进行设定, 从而调节相对应波长的分辨率。经过文献调研, 未见相关研究报道。

1 罗兰圆光学系统的色差来源

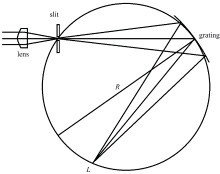
图1所示为以罗兰圆理论为基础建立的罗兰圆光学系统。根据罗兰圆理论, 当狭缝和凹面光栅都在罗兰圆上时, 通过凹面光栅进行衍射和聚焦后的各波长成像点都依次排列在罗兰圆上^[5]。

	Figure Option View Download New Window
	图1 罗兰圆光学系统Fig.1 Rowland circle optical system

在罗兰圆光学系统中需要使用平凸透镜将光线聚焦到狭缝上, 然而各波长的光线在同一种材料中折射率不同, 这使各波长的光线具有不同的焦距且各自的焦点产生了一定的偏移, 最终聚焦于狭缝前后的位置。最终导致色散后的各波长成像点也在罗兰圆附近同样也产生了一定量的偏移量, 使得各特征波长的成像点排列在一条曲面上, 由于新采集器件线阵CMOS或CCD这类平面感光面传感器代替光电倍增管的使用, 最终给系统产生了较严重的色差。

2 系统理论分辨率的分析

本文将光栅的固有分辨率和狭缝引起的增宽相结合, 计算出本系统在不考虑平凸透镜的影响下成像在罗兰圆上的理论最佳分辨率。该分辨率也是无色差情况下的理论最佳分辨率。之后该值与优化后的实际分辨率进行对比, 从而验证本研究所提及优化方法的科学性。首先根据瑞利判据, 当两个相差Δλ波长的光正好可分辨时, 其满足

$Δ λ = \frac{Δ λ}{Δ l} Δ l = \frac{d λ}{d l} Δ l = \frac{d λ}{d l} r$ (1)

式(1)中, r为光斑半径, 当Δl=r时系统正好处于可分辨的情况。光斑半径r可定义为^[6]

$r = r_{1} + r_{2} + r_{3}$ (2)

式(2)中, r₁为衍射宽度, r₂为狭缝像宽, r₃则是由几何位置产生的像差所增加的像宽。由于只计算成像于罗兰圆上的理论分辨率, 因此不考虑离焦像差, 故此r₃=0。其中r₁和r₂满足^{[6, 7]}

$r_{1} = f \cos β Δ β$ (3)

$r_{2} = s \frac{d λ}{d l}$ (4)

式(3)中, 半角宽Δβ 满足

$Δ β = \frac{λ}{Nd \cos β}$ (5)

通过式(5), 式(3)可化简为

$r_{1} = \frac{fλ}{Nd}$ (6)

式(6)中, f为凹面光栅的曲率半径401.56 mm, d为光栅常数1/2 400 mm, N为光栅总刻线数, Nd为光栅直径35 mm。波长λ可定为170~410 nm, 因此可计算得衍射像宽r₁的范围为1.950~4.704 μm。另外式(4)中, S为狭缝宽度20 μm, i为入射角42°, 级次m为1, 根据光栅光程可得到式(7), 由其可计算出衍射角β 的取值为-15.137°~18.353°。

$β = \arcsin (mλ 10^{- 6} \times 2 400 - \sin 42 °)$ (7)

此外关于式(1)和式(4)中的线色散率dl/dλ可定义为

$\frac{d l}{d λ} = f \frac{d β}{d λ} = \frac{fm}{d \cos β} = \frac{0.964}{\cos β}$ (8)

由式(8)计算出角色散率的倒数取值范围为0.985~1.038, 代入式(4)可确定狭缝像宽r₂为19.698~20.753 μm。因此光斑半径r为21.648~25.457 μm。

将光斑半径r代入式(1)便可确定波长170~410 nm范围内最终成像在罗兰圆上的分辨率为0.021~0.026 nm。

基于以上结论, 可以推导出单波长的理论分辨率的计算公式为

$Δ λ = (0.012 λ \cos β + 21.535 co s^{2} β) \times 10^{- 3}$ (9)

式(9)中, β 为各波长λ对应的衍射角, 通过该公式可计算出一些重要元素的最佳理论分辨率。如P元素分辨率为0.022 3 nm、 S元素分辨率为0.022 4 nm以及C元素分辨率为0.022 9 nm。

3 系统色差校正

为了优化第一章描述的系统色差, 本文提出了一种基于加权最小二乘法拟合像面的方法。

第一步, 根据式(7)得到各特征波长的衍射角如表1所示。

表1 各波段内特征波长相关参数 Table 1 Related parameters of characteristic wavelengths in each spectral band

第二步, 进行波段的划分以及中心波长的设定, 如表1所示, 系统共划分了七个波段。关于波段划分的主要判据为衍射角跨度保持在2°左右即可, 这将关系到最终的优化效果。随之将每个波段中最大和最小波长衍射角的均值作为该波段的中心波长衍射角。

第三步, 透镜参数优化。以第一波段内所有特征波长作为参数, 在Zemax中对以CaF₂为材料的平凸透镜进行波前优化(Wavefront), 其曲率半径的优化结果为53.626 mm。并且各波长在CaF₂玻璃中折射率n(λ)的Schott公式可表示为

$\{\begin{array}{l} n (λ) = \sqrt[]{a_{0} + a_{1} λ^{2} + a_{2} λ^{- 2} + a_{3} λ^{- 4} + a_{4} λ^{- 6} + a_{5} λ^{- 8}} \\ a_{0} = 2.040 \\ a_{1} = - 5.197 \times 10^{- 9} \\ a_{2} = 6.041 \times 10^{3} \\ a_{3} = 6.361 \times 10^{7} \\ a_{4} = - 5.744 \times 10^{10} \\ a_{5} = 1.605 \times 10^{16} \end{array}$ (10)

第四步, 计算各波长在聚焦时产生的偏移量。图2为本系统平凸透镜聚焦光学系统的上半部分, 光线从曲面Ah入射, 从平面CX出射。

	Figure Option View Download New Window
	图2 平凸透镜聚焦系统示意图Fig.2 Schematic diagram of a plano-convex lens focusing system

A点为光斑边界在子午面上的投影点, 直线oA为边界入射光线的法线。通过几何关系可得到边缘入射光线在透镜曲面的入射角i₁为

$i_{1} = acrsin \frac{D / 2}{r_{1}}$ (11)

式(11)中, r₁为曲率半径53.626 mm, D为通光孔径10 mm, 可得入射角i₁为5.35°。由于在同一个平凸透镜中各波长焦距不同, 因此可得焦距EFL是一个关于λ的方程, 其满足

$\{\begin{array}{l} EFL (λ) = X - r_{1} + \\ \sqrt[]{r_{1}^{2} - {(\frac{D}{2})}^{2}} + \frac{\frac{D}{2} \sqrt[]{1 - n^{2} M^{2}} \sqrt[]{1 - M^{2}}}{nM} - \\ \frac{\sqrt[]{1 - n^{2} M^{2}} (X - r_{1} + \sqrt[]{r_{1}^{2} - {(\frac{D}{2})}^{2}})}{n} \\ M = \frac{\frac{D}{2} \sin i_{1}}{r_{1} n} (\sqrt[]{{(\frac{n}{\sin i_{1}})}^{2} - 1} - \sqrt[]{{(\frac{r_{1}}{D / 2})}^{2} - 1}) \end{array}$ (12)

式(12)中, X为透镜厚度2.660 mm, r₁为透镜曲率半径53.626 mm, D为入孔的通光孔径10 mm, n为各波长λ对应的折射率, M为一个关于波长λ的表达式。

通过平凸透镜聚焦, 焦点正巧位于狭缝中心处的波长焦距EFL为105.710 mm, 该波长的焦距与其他波长焦距之差称为偏移距。 170~410 nm之间所有相关元素特征波长的偏移距如表1中的偏移距相关参数所示。通过透镜聚焦产生的偏移也导致原本各波长应聚焦在罗兰圆上的成像点位置发生了一定量的偏移。表1中偏移距大于0的波长其最终成像点沿着光线传播方向发生偏移, 反之则往相反方向偏移。

第五步, 像面拟合。图3给出了以第一波段为例的像面偏移轨迹图, 图中蓝色曲线为各波长最终成像点偏移后所形成的轨迹曲线, 黑色曲线为罗兰圆边界线。其中P、 S和B元素偏移量小于0, 因此这三种元素的波长成像点从罗兰圆上偏移到罗兰圆内侧。相反, 其余4种元素偏移到了罗兰圆外侧。

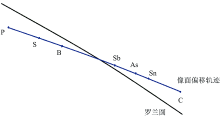	Figure Option View Download New Window
	图3 第一波段各波长成像点偏移轨迹图Fig.3 Trajectory diagram of imaging point shift for each wavelength in the first band

如图3所示, 像面偏移轨迹最终呈现一个曲面, 而所用传感器感光面是一个平面, 因此可用最小二乘法将第一波段内所有特征波长偏移后的成像点拟合成一条直线, 以该直线作为传感器感光面在子午面上的投影。但在工业领域中某些元素常常被作为检测对象, 例如在第一波段中的C、 P和S三种元素, 然而使用最小二乘法拟合像面往往无法突出这些元素的分辨率。

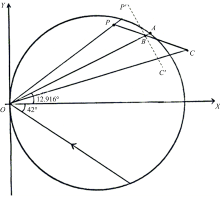
为了解决此问题, 本研究对像面采用了加权最小二乘法进行拟合, 该方法可以根据波长权值占比的大小对某些元素进行针对性的色差校正。为此建立一个以光栅中心为圆心的相对坐标系模型, 如图4所示。其中PC表示为拟合后的像面, OA是该波段中心波长的衍射光。中心偏移距AB就是该波段中心波长的衍射光在引入校正量后的偏移距离, 偏移倾斜角∠PBP'则是引入校正量后的旋转角, 二者都是在Zemax中仿真以及实际设计中进行色差校正的关键参数。

	Figure Option View Download New Window
	图4 第一波段衍射相对坐标系Fig.4 Relative coordinate system of diffraction for the first band

为了得到各波长的校正参数, 需要得出各波长最终成像点的相对坐标。为此需计算各波长偏移后的衍射光程Offset_DifPath(λ), 其满足

$Offset_DifPath (λ) = L_{β} + EFL (λ) = R \cos (β) + EFL (λ)$ (13)

式(13)中, L_β为各波长偏移前的衍射光程, R为光栅曲率半径, β 为各特征波长对应的衍射角。

结合各波长的偏移衍射光程和衍射角作为极坐标, 用来确定各波长成像点的相对位置, 然后通过基本三角函数式(14)将其转换为直角坐标。

$\{\begin{array}{l} X (λ) = Offset_DifPath (λ) \cos (β) \\ Y (λ) = Offset_DifPath (λ) \sin (β) \end{array}$ (14)

式(14)中, X(λ)和Y(λ)分别为不同波长成像点的横纵坐标。在使用加权最小二乘法进行拟合前, 需要为各波段中所有波长进行一个权值的分配。以第一波段为例, 该波段范围内各元素特征波长的权值设置为

$\begin{array}{l} Weight [0.33, 0.33, 0.002 5, 0.002 5, \\ 0.002 5, 0.002 5, 0.33] \end{array}$ (15)

式(15)中, 权值0.33为第一波段范围内P、 S和C三种较为重要的元素的权值比重, 0.002 5则是该波段内其他剩余元素。结合权值计算横纵坐标的加权平均值X_WeiMean和Y_WeiMean可表示为

$\{\begin{array}{l} X_WeiMean = \overset{n}{\sum_{i = 1}} X (λ_{i}) Weight (i) \\ Y_WeiMean = \overset{n}{\sum_{i = 1}} Y (λ_{i}) Weight (i) \end{array}$ (16)

每个横纵坐标相对于加权平均值的偏差ΔX(λ_i)和ΔY(λ_i)可表示为

$\{\begin{array}{l} Δ X (λ_{i}) = X (λ_{i}) - X_WeiMean \\ Δ Y (λ_{i}) = Y (λ_{i}) - Y_WeiMean \end{array}$ (17)

最后通过式(18)计算通过加权最小二乘法拟合像面后结果的斜率k和截距b。

$\{\begin{array}{l} k = \frac{\overset{n}{\sum_{i = 1}} Δ X (λ_{i}) Δ Y (λ_{i}) Weight (i)}{\overset{n}{\sum_{i = 1}} Weight (i) Δ X (λ_{i})^{2}} \\ b = Y_WeiMean - kX_WeiMean \end{array}$ (18)

使用MATLAB对第一波段各波长进行加权最小二乘法的拟合仿真, 得到斜率k和截距b分别为-1.262和568.621。拟合仿真结果如图5所示, 其中蓝色曲线为各波长偏移后实际成像点所在的曲线, 红色直线为最终的拟合结果, 该直线也是实际CMOS光电传感器感光面在子午面上的投影位置。图中呈现出P、 S和C三种元素的特征波长相比于其他波长明显具有更好的色差校正效果。

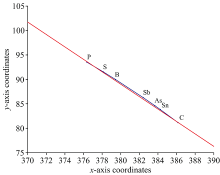	Figure Option View Download New Window
	图5 第一波段加权最小二乘法拟合像面示意图Fig.5 Schematic diagram of image plane for weighted least squares fitting in the first band

在得到拟合像面的斜率和截距后, 在以图4所示的坐标系参考下, 中心偏移距AB和偏移倾斜角∠PBP'满足

$\{\begin{array}{l} AB = \pm \sqrt[]{{(f co s^{2} (θ_Cen λ) + \frac{b}{\tan (θ_Cen λ) + k})}^{2} + {(\frac{1}{2} f \sin (2 θ_Cen λ) + \frac{b \tan (θ_Cen λ)}{\tan (θ_Cen λ) + k})}^{2}} \\ ∠ PBP' = \pm (\arctan \frac{k + \tan (θ_Cen λ)}{1 - k \tan (θ_Cen λ)} - 90 °) \end{array}$ (19)

式(19)中, f为光栅的曲率半径401.56 mm, 角θ_Cenλ为表1中各波段的中心波长衍射角, 并且k和b为像面拟合后的斜率和截距。由式(19)计算得到光学系统的各波段校正参数中心偏移距和偏移倾斜角的值如表2所示, 这两个参数主要用于Zemax仿真以及在实际设计时起到色差校正的作用。

表2 各波段色差校正参数 Table 2 Chromatic aberration parameters for each band

4 Zemax中的仿真结果

基于上述分析, 本文所设计的罗兰圆光学系统的基础参数如表3所示。以表中参数为基础建立罗兰圆光学系统, 再结合表3中的参数对系统进行色差校正后输入到Zemax光学软件中进行光线追迹仿真。

表3 罗兰圆光学系统性能参数 Table 3 Roland circular optical system performance parameters

并通过仿真得到的点列图及其变化曲线, 以及和光谱成像图这几个方面对系统设计的结果进行评价分析。图6(a)—(g)分别为七个波段的光程图; 图7为第一波段内各波长的点列图; 图8(a)和(b)分别为光学系统170~200 nm波段和200~410 nm波段范围内点列图在子午方向上的成像宽度关于波长的变化曲线。其中170~200 nm范围内的特征波长成像在第一波段的像面内, 在该波段内成像位于两端的P、 S和C三种元素较为重要, 使用加权最小二乘法拟合后这三种元素成像宽度达到最小(7 μm左右), 分辨率达到最佳。而位于第一波段靠近中心波长的B、 Sb两种元素的子午方向成像宽度虽然较大, 但基本也能保持在16 μm左右。形成图8中曲线走势的主要原因是第一波段包含的特征元素较多, 而重要元素成像点位于像面两端导致。而200~410 nm波段范围内的子午方向成像宽度基本保持在7~9 μm的范围内, 并没有太大的起伏。图9、 10分别为170~200和200~410 nm波长范围内线阵CMOS光电传感器上的全谱光谱图, 从该谱图结果可知各元素的特征波长与其相距0.02 nm的波长成像明显可以被分开。此结果表明各元素对应的特征波长的分辨率可以保持在0.02 nm左右, 此结果接近于由式(9)计算得到的各波长理论分辨率, 并且在第一波段中P、 S和C三种元素被分开的程度明显优于该波段其余元素。以上结果说明加权最小二乘法拟合像面对于消除色差的科学性。

	Figure Option View Download New Window
	图6 各波段的光程图 (a): 第1波段; (b): 第2波段; (c): 第3波段; (d): 第4波段; (e): 第5波段; (f): 第6波段; (g): 第7波段Fig.6 The optical path diagram for each wavelength band (a): Band 1; (b): Band 2; (c): Band 3; (d): Band 4; (e): Band 5; (f): Band 6; (g): Band 7

	Figure Option View Download New Window
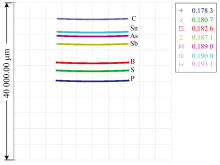	图7 第1波段P、 S、 B、 Sb、 As、 Sn和C元素特征波长的点列图Fig.7 Spot diagrams of characteristic wavelengths for elements P, S, B, Sb, As, Sn, and C in wavelength band 1

	Figure Option View Download New Window
	图8 各波长成像宽度变化曲线 (a): 170~200 nm波段; (b): 200~410 nm波段Fig.8 Curve of imaging width variation for each wavelength (a): 170~200 nm band; (b): 200~410 nm band

	Figure Option View Download New Window
	图9 线阵CMOS上的170~200 nm光谱图Fig.9 Spectral graph of 170~200 nm on a linear CMOS array

	Figure Option View Download New Window
	图10 线阵CMOS上的200~410 nm光谱图Fig.10 Spectral graph of 200~410nm on a linear CMOS array

基于上述讨论, 本罗兰圆光学系统能在170~410 nm范围内全谱成像于7片感光面为0.2 mm×28.67mm的线阵CMOS光电传感器上(HAMAMATSU公司的S13496), 满足最初设定的光谱仪分辨率0.02 nm的性能指标。

5 结论

以罗兰圆理论为基础的光学色散系统成像点依次排列在罗兰圆上, 其本身属于曲面成像。由于CMOS或CCD这类传感器的感光面是一个平面, 因此结果具有一定的色差。此外由于平凸透镜引起的成像点偏移, 这二者叠加使最终成像的色差加剧。利用加权最小二乘法拟合像面的方法对系统的色差进行校正, 并通过同一波段内各特征波长权值的设定, 可以对特定元素波长进行突出色差校正。最终实现在170~410 nm紫外波段范围内各特征波长分辨率保持在0.02 nm, 基本接近于本系统无色差影响下的理论最佳分辨率。本文提出的校正方法对光学系统存在严重色差时提供一个最优的解决方案。

参考文献

文献列表

[1]	HUANG Liang-kun, WEN Quan, WEN Zhi-yu, et al(黄良坤, 温泉, 温志渝, 等). Laser & Optoelectronics Progress(激光与光电子学进展) , 2020, 57(5): 053003. [本文引用:1]
[2]	MO Xiang-xia, WEN Zhi-yu, ZHANG Zhi-hai, et al(莫祥霞, 温志渝, 张智海, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2011, 31(12): 3412. [本文引用:1]
[3]	XU Yong-lin, LIANG Xiao, ZHANG Dong-sheng(徐永林, 梁潇, 张东生). Metallurgical Analysis(冶金分析) , 2013, 33(10): 19. [本文引用:1]
[4]	GUO Fei-fei, XU Peng, CUI Fei-peng, et al(郭飞飞, 徐鹏, 崔飞鹏, 等). Metallurgical Analysis(冶金分析), 2020, 40(12): 94. [本文引用:1]
[5]	LU Yi, REN Wan-jie, GUO Guo-jian, et al(鲁毅, 任万杰, 郭国建, 等). Journal of Applied Optics(应用光学), 2022, 43(3): 415. [本文引用:1]
[6]	YU Chang-qing, LIU Jie, LI Jia-ze(于常青, 刘杰, 李家泽). Optical Technique(光学技术), 2001, (2): 97. [本文引用:2]
[7]	CHEN Jian-bo, YANG Xiao-hu, SUN Yu-lai, et al(陈建波, 杨小虎, 孙昱来, 等). Chinese Journal of Scientific Instrument(仪器仪表学报), 2023, 44(2): 59. [本文引用:1]