引用本文
李荣, 曹冠龙, 蒲源, 邱波, 王晓敏, 闫静, 王坤. TDSC-Net: 一种基于注意力机制与特征融合的二维恒星光谱分类模型[J]. 光谱学与光谱分析, 2024,44(7): 1968-1973.
LI Rong, CAO Guan-long, PU Yuan, QIU Bo, WANG Xiao-min, YAN Jing, WANG Kun. TDSC-Net: A Two-Dimensional Stellar Spectra Classification Model Based on Attention Mechanism and Feature Fusion[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1968-1973.
Doi:10.3964/j.issn.1000-0593(2024)07-1968-06  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
TDSC-Net: 一种基于注意力机制与特征融合的二维恒星光谱分类模型
李荣1, 曹冠龙1,*, 蒲源2,*, 邱波1, 王晓敏1, 闫静1, 王坤1
1.河北工业大学, 天津 300400
2.广东白云学院, 广东 广州 510450
*通讯作者 e-mail: caoguanlong@hebut.edu.cn; puyuan@baiyunu.edu.cn

作者简介: 李 荣,女, 1997年生,河北工业大学硕士研究生 e-mail: 964907771@qq.com

收稿日期: 2023-05-22 修回日期: 2023-09-18
基金: 天津市自然科学基金项目(22JCYBJC00410),国家自然科学基金委员会-中国科学院天文联合基金项目(U1931134)资助
摘要

面对信噪比较低的天体, 传统一维光谱的分类效果很差。 因此, 从二维光谱出发, 提出了结合注意力机制的特征融合模型TDSC-Net(two-dimensional spectra classification network)用于恒星分类。 TDSC-Net通过完全相同的特征提取层分别对恒星蓝端和红端的二维光谱图像进行特征提取, 之后针对这些特征进行融合, 然后进行分类。 本文实验中的恒星光谱数据选自LAMOST(the large sky area multi-object fiber spectroscopic telescope)数据库, 预处理采用Z-score进行光谱归一化, 以减少由于光谱流量值差别大造成的模型收敛困难问题。 使用精确率(Precision)、 召回率(Recall)、 F1-score和准确率(Accuracy)四个指标来评估模型性能。 实验包括: 第一部分利用TDSC-Net进行A、 F、 G、 K、 M型恒星分类, 以验证利用二维光谱对恒星多分类的可靠性; 第二部分将二维光谱按照不同的信噪比区间进行分类, 以探究信噪比对分类准确率的影响。 第一部分的结果表明, 进行五分类总的准确率达到84.3%。 其中, A、 F、 G、 K、 M各自的分类精度分别为87.0%, 84.6%, 81.2%, 87.4%, 89.7%, 均优于自行抽谱后的一维光谱分类结果。 第二部分的结果表明, 即使在SNR<30的低信噪比区间, 二维光谱分类准确率仍然可以达到78.9%; 而当SNR>30之后, 信噪比对光谱分类的影响就不明显了。 由此证明了低信噪比时使用二维光谱分类的重要性以及TDSC-Net对恒星光谱分类的有效性。

关键词: 恒星分类; 卷积神经网络; 注意力机制; Two-dimensional spectra classification network
中图分类号:P157.2 文献标志码:A
TDSC-Net: A Two-Dimensional Stellar Spectra Classification Model Based on Attention Mechanism and Feature Fusion
LI Rong1, CAO Guan-long1,*, PU Yuan2,*, QIU Bo1, WANG Xiao-min1, YAN Jing1, WANG Kun1
1. Hebei University of Technology, Tianjin 300400, China
2. Guangdong Baiyun University, Guangzhou 510450, China
*Corresponding authors
Abstract

Traditional one-dimensional spectra perform poorly when classifying celestial objects with a low signal-to-noise ratio (SNR). Therefore, the paper uses two-dimensional spectra and proposes a feature fusion model called TDSC-Net (Two-Dimensional Spectra Classification Network), incorporating an attention mechanism for stellar classification. TDSC-Net employs identical feature extraction layers to get features from the two-dimensional spectra of stars, specifically from the blue and red ends. The extracted features are fused and employed for the classification task. The stellar spectral data in this experiment is selected from the LAMOST (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope) database. They are using Z-score normalization on the spectra to reduce convergence difficulties caused by significant variations in spectral flux values and evaluating the model performance by four metrics: Precision, Recall, F1-score, and Accuracy. The experiments consist of two parts: In the first part, TDSC-Net is employed to classify A, F, G, K, and M-type stars to validate the reliability of using two-dimensional spectra for multi-class stellar classification. In the second part, the two-dimensional spectra are classified based on different SNRs to investigate the impact of SNRs on classification accuracy. The first part’s results show that the five-class classification accuracy reaches 84.3%. The classification accuracies of A, F, G, K, and M types are 87.0%, 84.6%, 81.2%, 87.4%, and 89.7%, respectively. These accuracies are higher than the results obtained from one-dimensional spectra classification after spectra extraction. The results of the second part indicate that even in the low SNR (SNR<30), the accuracy of two-dimensional spectra classification can still reach 78.9%. Once the SNR surpasses 30, the impact of SNR on spectra classification becomes less significant. These provide evidence for the importance of using two-dimensional spectra classification in low SNR and demonstrate the effectiveness of TDSC-Net in stellar spectra classification.

Keyword: Stellar classification; Convolutional neural network; Attention mechanism; Two-dimensional spectra classification network
引言

随着科学技术的水平不断提高, 多个巡天项目获取天文数据的数量呈指数趋势增加。 我国的大天区面积多目标光纤光谱天文望远镜(LAMOST)成功应用“多目标光谱光纤”[1]观测技术, 可以在一次曝光获得4 000多个光谱, 成为世界上光谱获取率最高的望远镜。 如何高效地对如此海量的数据进行信息挖掘成为天文学家面对的挑战。 光谱中包含着许多有价值的天文信息, 其中利用光谱对恒星进行准确分类是对天文数据研究的一项重要内容。 广泛使用的一种传统恒星分类算法是基于MK(Morgan-Keenan)系统[2]进行分类的, MK系统主要依照恒星的温度对其进行分类, 在这一标准下, 根据温度由高到低, 可以将恒星分为O、 B、 A、 F、 G、 K、 M七种类型。

MK系统中, 几乎所有的恒星都是通过人眼辨别的, 这种处理方法在处理大量数据时效率低下, 已经不能满足如今的大数据时代。 近些年随着机器学习的发展, 尤其是深度学习的出现, 国内外的研究人员在对星体进行自动分类的方法做出了诸多尝试。 屠良平[3]等提出基于局部均值的K-近质心近邻(local mean-based K-nearest centroid neighbor, LMKNCN)算法, 对恒星、 星系以及类星体进行分类, 平均准确率超过K-近邻、 K-近质心近邻算法, 达到了98.1%。 Xing[4]等首先利用小波去噪去除恒星光谱的噪声, 之后利用支持向量机(support vector machine, SVM)进行分类, 分类效果优于单独使用SVM或SVM结合PCA降维法。 Li[5]等利用基于随机森林(random forest, RF)的光谱分类算法来进行恒星分类, 最终表现出较良好的分类性能。 Zhao[6]等设计了ECNN(ensemble convolutional neural network)来对恒星进行分类, 分类精度可以达到95%, 超过了经典的主成分分析法和支持向量机模型。 洪舒欣[7]等提出了基于卷积神经网络的CSSL_CNN(classification model of stellar spectral type and luminosity type based on convolution neural network)模型, 用来实现恒星光谱型和光度型的二元分类, 准确率为83.19%, 在算法性能上优于模板匹配法。 Zou[8]等设计了RAC-Net(A residual and attention based convolutional network)模型, 通过引入残差模块, 解决由于网络层数过多引起的梯度消失或者梯度爆炸的问题, 在进行恒星、 星系、 类星体的分类任务时, 实验结果表明, RAC-Net的分类效果要优于无残差模块的卷积神经网络。

目前大多数的学者都是使用一维光谱进行相关研究, 不容忽视的是, 二维光谱得到一维光谱时, 需要进行抽谱以及在一维层面的波长定标和减天光等操作, 由二维降到一维的过程, 必然会丢失二维光谱本身的信息。 一维光谱使用一维卷积对其进行处理, 也不能够充分利用卷积神经网络在图像分类识别上的优势[9]。

本文搭建了恒星分类模型TDSC-Net, 该模型可以直接利用二维光谱图像对恒星进行分类, 之后还探究了二维光谱的信噪比对分类准确率的影响。

1 二维光谱数据和预处理
1.1 二维光谱数据

LAMOST天文望远镜可以观测的光谱波长覆盖范围为370~900 nm, 进入到光谱仪中的光束会被LAMOST装置中的分色镜分为蓝端(370~590 nm)和红端(570~900 nm)[10]。

同一条光谱的信息被分到不同波长区间的蓝端和红端, 两端光谱经过合并后可以得到一条包含完整信息的光谱。 当光纤瞄准目标天体曝光后得到的光谱图像称为目标谱, 如图1所示。 目标谱中包含250根光纤光谱, 由于不同光谱之间排列紧密, 所以会出现交叉污染的现象, 特别是当光谱附近有强星等的光纤光谱时, 这一现象将更加严重。 单根光纤光谱对应的长度为4 136像素, 宽度为15像素。 在目标谱中截取部分长度的一根二维光谱的示意图如图2, 在宽度方向上, 像素块的明亮程度由中心向两边递减。 本文为了尽可能多地保留二维光谱所包含的信息, 同时减少相邻光谱间交叉污染现象带来的不良影响, 在单根光谱的长度方向上像素值为4 136, 在宽度方面, 仅利用中间较为明亮的11个像素作为输入数据。

图1 目标谱Fig.1 The spectrum of object

图2 单根二维光谱图Fig.2 A single image of two-dimensional spectrum

1.2 预处理

对于不同的二维光谱, 在相同的波长点下对应的光谱流量值可能差别非常大, 这样的差异会影响后续的分类效果。 因此, 需要对二维光谱图像进行归一化, 消除由于流量值变化区间处于不同数量级造成的问题。 本文采用零均值归一化Z-score, 使最终的数据满足均值为0, 方差为1的正态分布, 归一化的公式为

z=x-μσ(1)

式(1)中, x是原始数据, μ是原始数据的均值, σ 是原始数据所对应的方差, z是经过归一化后的数据。

2 网络结构
2.1 二维光谱恒星分类网络(TDSC-Net)

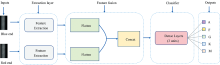
本文提出了基于二维光谱图像的恒星分类网络TDSC-Net。 在LAMOST二维光谱中, 同一天体有蓝端和红端两种分别分布在不同波长范围的数据。 只是依靠某一端图像的信息不足以得到足够的信息, 故为充分利用处于不同波长光谱包含的信息, 获得更高的分类精度, 利用蓝端和红端进行特征级融合的思想搭建了本文的TDSC-Net, 该网络由三个主要部分组成, 结构如图3所示。

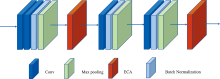
图3 TDSC-Net模型Fig.3 The structure of TDSC-Net

第一部分为特征提取网络, 如图4所示。 具体的网络结构介绍如下: 特征提取网络由四个卷积层、 三个归一化网络层以及三个最大池化层构成。 其中, 卷积层用来提取输入数据的特征, 池化层对经过卷积后得到的特征图进行压缩, 在提取主要特征的同时减小特征图的尺寸。 同时为了使模型更加关注有用的信息, 在第一个和最后一个池化层的后面添加了ECA(efficient channel attention)注意力模块, 有效提高了分类网络的准确率。

图4 特征提取层Fig.4 Feature extraction layer

第二部分为特征融合层, 本文设计的TDSC-Net是一个对称的网络模型。 蓝端和红端的光谱图像分别经过特征提取层后, 将得到的特征图展平后融合, 进而获得新的、 更易于分类的特征。

第三部分为全连接层, 将前面获得的特征送入到该层, 为了防止过拟合, 三个全连接层之间使用Dropout机制, 使训练时的神经元以0.5的概率随机失活, 提高模型的鲁棒性。

2.2 ECA-Net

ECA-Net[11]是一个通道注意力模块, 结构如图5所示。 它不同于以往其他以复杂度换取优良性能的注意力模块, 可以仅利用少量的参数, 就实现明显的性能提升, 属于轻量级的模块。 首先利用全局平均池化GAP(global avg pooling)得到1×1×C大小的特征图, 然后计算得到自适应的卷积核大小, 之后将该卷积核应用到一维卷积中, 获得特征图中每个通道对应的权重, 最后将权重与原特征图相乘, 使网络集中在重要的特征并加以挖掘。

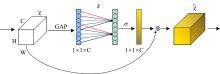图5 ECA模块[11]Fig.5 The structure of ECA

2.3 特征级融合

在利用卷积神经网络提取特征后, 有四种特征融合的方式: 特征级融合、 模型级融合、 决策级融合以及混合级融合。 LAMOST二维光谱图像包含蓝端和红端数据, 如果只是利用其中一端的图像将不能对一个天体进行全面的分析。 另一方面, 深度学习的训练可以认为是一个寻找全局最优解的过程, 而一些超参数却会导致模型陷入局部最优, 从而影响模型进一步优化, 特征级融合的方式有助于减少该问题的发生。 因此, 本文使用了特征级的融合方式。

3 结果与讨论

所有程序均采用python语言编写, 学习框架为pytorch1.7。 实验运行在Intel Core I5处理器, 16GRAM, 为了提高算法的运算速度, 使用RTX 2080 Ti在64位的windows系统下加速计算。

实验中使用的数据是来自LAMOST的恒星二维光谱。 第一部分的实验数据集共包括953个A型恒星, 4 362个F型恒星, 6 912个G型恒星, 4 407个K型恒星, 1 390个M型恒星。 第二部分实验中, 统计目前已有单根二维光谱数据分布在不同信噪比区间的恒星数量如图6所示, 可以看到M型恒星在SNR>60的区间只有64个样本, 与其他类型的恒星数量相差悬殊, 为充分利用已有的二维光谱, 因此第二部分实验仅对A、 F、 G、 K四类恒星进行分类。 信噪比区间分为SNR<30, 30<SNR<60, SNR>60。 在每个信噪比区间内, 选取A型恒星的数据量为200, F型、 G型、 K型恒星的数据量依次为700、 1 500和1 100。 以上恒星均有蓝端和红端光谱图像。 在实验时将数据集按照8∶1∶1的比例分别划分为训练集、 验证集和测试集。

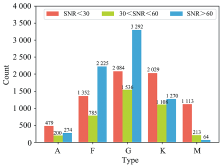图6 不同信噪比区间二维光谱的数量Fig.6 The number of two-dimensional spectra in different signal-to-noise ratio intervals

为了解决数据集的不平衡问题, 实验过程采用带权重的交叉熵损失函数, 给样本较少的类赋予更多的权重, 在网络预测出错的时候, 就会受到更多的惩罚, 对于样本较多的类则给较小的权重。 交叉熵损失函数的公式如式(2)

loss(x, class)=weight[class](-x[class]+log(∑jexp(x[j])))(2)

在本文中, 这里的weight[class]以各自样本数的倒数作为权重。

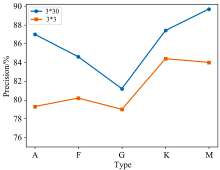
在深度学习领域中, 通常采用的卷积核大小为3×3, 或者5×5等正方形卷积核, 但本文处理的二维光谱图像的大小为11×4 136, 长宽比非常悬殊, 常用大小的卷积核无法满足充分提取图像特征的需求。 图7为分别采用3×3和3×30的卷积核得到的分类情况, 分类结果表明, 对于长宽比悬殊的单根二维光谱, 相较于3×3的卷积核, 使用3×30的卷积核可以获得更高的分类准确率, 有着更好的感受野, 可以充分利用区域中的上下文信息, 有效提取出有利于图像分类的特征。

图7 使用不同大小的卷积核对应的分类精确率Fig.7 Classification precision using convolutional kernels of different sizes

二维光谱经过归一化预处理之后, 将其放入TDSC-Net模型中训练, 进行恒星A、 F、 G、 K、 M分类。 图8(a)和(b)分别展示了训练过程中训练集和测试集的损失值和准确率的变化曲线, 从图中可以明显地看到, 迭代60次可以使准确率稳定, 前10次准确率快速增长, 之后准确率呈现缓慢增长的趋势。 本文提出的TDSC-Net可以使恒星二维光谱分类达到较高的准确率。 分类得到的精确率、 召回率、 F1-score和准确率如表1所示。

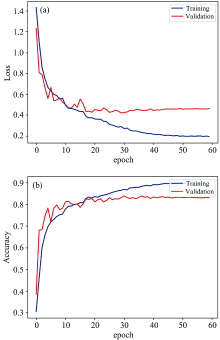图8 TDSC-Net训练集和验证集的损失函数曲线和准确率
(a): 损失函数曲线; (b): 准确率Fig.8 Curves of TDSC-Net’ s loss and accuracy for the training set and validation
(a): Loss curves; (b): Accuracy

表1 TDSC-Net的精确率、 召回率、 F1-score和准确率 Table 1 The precision, recall, F1-score, and accuracy of TDSC-Net

由表1的实验结果可知, 二维光谱可以用于恒星光谱的多分类, 不需要像一维光谱要经过复杂的抽谱等过程, 在二维图像层面上便可以有效地进行分类。 在表1中, TDSC-Net对M型恒星的分类精确率最高, 达到89.7%, A型恒星和K型恒星的分类精确率较高, F型恒星次之, 而G型恒星的分类结果相对较差, 分类精确率为81.2%。

为了说明ECA注意力模块对整个模型的影响, 本文做了消融实验作为对比。 利用测试集预测后得到的混淆矩阵如图9所示。 其中每一行表示样本的真实标签, 每一列指分类预测后所属的类别。 通过混淆矩阵可以看出, 预测结果大部分都沿主对角线呈现, 误分类的恒星主要集中在相邻的类型, 主对角线上的数量依次为1 519和1 496。 在测试集相同的基础上, 图9(a)中沿对角线分布的数量高于图9(b), 意味着同时使用蓝端和红端二维光谱并加入ECA注意力模块, 达到了最优的分类性能。 这说明ECA模块的加入, 可以使模型的特征提取能力变得更强, 使分类准确率更高。

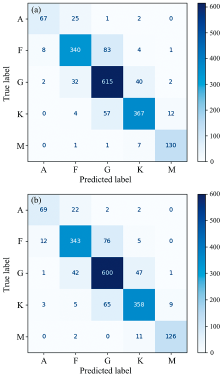图9 分类混淆矩阵
(a): TDSC-Net混淆矩阵; (b): 无ECA的混淆矩阵Fig.9 Classification confusion matrix
(a): Confusion matrix of TDSC-Net; (b): Confusion matrix of TDSC-Net without ECA

本文进行了与用一维光谱的对比实验进一步说明二维光谱用于分类的优越性。 利用孔径抽谱法[12]对二维光谱抽谱得到一维光谱, 没有进行后续的波长定标以及减天光等复杂的步骤。 采用RAC-Net[8]和1D SSCNN[13](1D stellar spectra convolutional neural network)对一维光谱进行分类, 实验结果如表2所示。 可以看到A、 F、 G、 K、 M五类恒星在二维光谱的分类精度均高于一维光谱。

表2 分类精确率实验结果比较 Table 2 Comparison of experimental results of classification precision

为了研究不同信噪比对于TDSC-Net分类性能的影响, 本文选取了处于不同信噪比区间SNR<30, 30<SNR<60, SNR>60的A、 F、 G、 K型四类恒星进行分类。 在不同的信噪比区间内, 对应的分类准确率分别为78.9%, 85.1%, 86.6%, 每一类恒星具体的分类结果如图10所示。

图10 不同信噪比区间的分类结果Fig.10 Classification results of different SNR intervals

二维光谱可能由于信噪比太低而无法获得有效的一维光谱, 之前只用一维光谱研究的思路可能会丢弃此类光谱, 造成资源浪费。 图10的实验结果表明, 即使在SNR<30的低信噪比区间, A、 F、 G、 K的分类精度也可以达到相对不错的水平, 其中K型恒星的分类精度可达86.0%。 在30<SNR<60和SNR>60的信噪比区间, 整体的分类准确率差别变化小, 仅为1.1%。 其中可能的原因是当信噪比高于30左右时, 分类时二维光谱受到自身背景的影响变小, 从而最终的分类准确率变化不大。

4 结论

尝试直接利用二维光谱进行恒星的多分类, 打破以往只用一维光谱进行分类的固有思维。 结合LAMOST二维光谱图像分为蓝端和红端的特点, 搭建了TDSC-Net, 该模型由两个支路构成, 分别提取蓝端和红端的特征后再进行融合。 实验结果表明, 得到的特征是可以有效地对A、 F、 G、 K、 M类型的恒星进行多分类的, 分类准确率为84.3%, 相较一维光谱更高, 验证了二维光谱的优越性。 本文还对处于不同信噪比区间的A、 F、 G、 K类型的恒星分类, 可以看到在SNR<30的低信噪比区间也可以得到较高的准确率。 总之, 二维光谱相较一维光谱可以保留更多的信息, 利用TDSC-Net对二维恒星光谱分类是有效的。

未来, 我们计划将减天光的相关工作应用于二维光谱中, 以期在低信噪比区间达到更高的分类准确率。

参考文献
[1] Lu Y, Luo A L, Wang L L, et al. Astronomy and Computing, 2021, 36: 100485. [本文引用:1]
[2] Kheirdastan S, Bazarghan M. Astrophysics and Space Science, 2016, 361(9): 304. [本文引用:1]
[3] TU Liang-ping, WEI Hui-ming, WANG Zhi-heng, et al(屠良平, 魏会明, 王志衡, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(4): 1103. [本文引用:1]
[4] Xing F, Guo P. Advances in Neural Networks-ISNN 2004, PT1, 3173: 616. [本文引用:1]
[5] Li X R, Lin Y T, Qiu K B. Research in Astronomy and Astrophysics, 2019, 19(8): 111. [本文引用:1]
[6] Zhao Z, Wei J Y, Jiang B. Advances in Astronomy, 2022, 2022: 4489359. [本文引用:1]
[7] HONG Shu-xin, ZOU Zhi-qiang, XU Ling-zhe(洪舒欣, 邹志强, 徐灵哲). Acta Astronomica Sinica(天文学报), 2021, 62(5): 16. [本文引用:1]
[8] Zou Z Q, Zhu T C, Xu L Z, et al. Publications of the Astronomical Society of the Pacific, 2020, 132(1010): 044503. [本文引用:2]
[9] He K, Zhang X, Ren S, et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 770. [本文引用:1]
[10] Cui X Q, Zhao Y H, Chu Y Q, et al. Research in Astronomy and Astrophysics, 2012, 12(9): 1197. [本文引用:1]
[11] Wang Q, Wu B, Zhu P, et al. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020: 11531. [本文引用:1]
[12] Cui B, Ye Z, Bai Z. Chinese Astronomy and Astrophysics, 2009, 33(1): 99. [本文引用:1]
[13] Liu W, Zhu M, Dai C, et al. Monthly Notices of the Royal Astronomical Society, 2019, 483(4): 4774. [本文引用:1]