引用本文
王安, 崔佳诚, 宋惟然, 侯宗余, 陈祥, 陈斐. 基于激光诱导击穿光谱与半监督学习的煤质定量分析研究[J]. 光谱学与光谱分析, 2024,44(7): 1940-1945.
WANG An, CUI Jia-cheng, SONG Wei-ran, HOU Zong-yu, CHEN Xiang, CHEN Fei. Quantitative Analysis of Coal Properties Using Laser-Induced Breakdown Spectroscopy and Semi-Supervised Learning[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1940-1945.
Doi:10.3964/j.issn.1000-0593(2024)07-1940-06  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于激光诱导击穿光谱与半监督学习的煤质定量分析研究
王安1, 崔佳诚2, 宋惟然2, 侯宗余2,3,*, 陈祥4, 陈斐4
1.国能常州发电有限公司, 江苏 常州 213001
2.新型电力系统运行与控制全国重点实验室, 清华大学能源与动力工程系, 教育部低碳清洁能源创新国际合作联合实验室, 北京 100084
3.清华大学山西清洁能源研究院, 山西 太原 030032
4.南京国电环保科技有限公司, 江苏 南京 210061
*通讯作者 e-mail: houzy@tsinghua.edu.cn

作者简介: 王 安, 1981年生,国能常州发电有限公司高级工程师 e-mail: wanga2003@sina.com

收稿日期: 2022-10-03 修回日期: 2023-10-11
基金: 国家自然科学基金项目(51906124)资助
摘要

激光诱导击穿光谱(LIBS)是一项新兴的原子光谱分析技术, 具有无需复杂样品制备, 快速、 原位、 多元素同时测量等优点, 在煤质分析领域展现出良好的应用前景。 近年来, 化学计量学和机器学习模型被广泛用于煤质分析。 而这些模型通常依赖于一定数量的训练样本来确保分析结果的精度和可靠性。 由于获取煤样的真实的成分含量信息(标签)需要复杂、 耗时的化学分析, 训练样本数量不足, 导致模型性能欠佳。 针对小样本情况下基于LIBS技术的煤质分析, 提出了多模型集成的半监督学习方法提升定量分析性能。 首先根据初始训练集建立5个基线模型, 包括多元线性回归(MLR)、 偏最小二乘回归(PLSR)、 局部加权偏最小二乘回归(LW-PLSR)、 支持向量回归(SVR)、 核极限学习机(K-ELM); 利用5个模型处理无标签数据, 得到5组预测值; 对于每个无标签样本, 计算5个预测值的标准差, 并将最小标准差对应的无标签样本加入训练集, 其伪标签为5个预测值的平均值; 通过迭代循环来扩充训练集, 并更新、 优化训练模型; 最后对测试样本进行分析。 提出的方法在LIBS煤质分析数据集上进行了测试, 包含20个训练样本、 39个测试样本、 280个无标签样本。 结果表明, 提出的半监督学习方法将固定碳、 灰分、 挥发分含量的预测拟合系数( R2)分别提高了0.033、 0.102和0.118。 在训练样本数量不足的条件下, 半监督学习能够有效提升了LIBS定量化模型的准确度和可靠性。

关键词: 激光诱导击穿光谱; 半监督学习; 煤炭; 定量分析
中图分类号:O657.38 文献标志码:A
Quantitative Analysis of Coal Properties Using Laser-Induced Breakdown Spectroscopy and Semi-Supervised Learning
WANG An1, CUI Jia-cheng2, SONG Wei-ran2, HOU Zong-yu2,3,*, CHEN Xiang4, CHEN Fei4
1. Guodian Changzhou Power Generating Co., Ltd., Changzhou 213001, China
2. State Key Lab of Power Systems, International Joint Laboratory on Low Carbon Clean Energy Innovation, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
3. Shanxi Research Institute for Clean Energy, Tsinghua University, Taiyuan 030032, China
4. Nanjing Guodian Environment Protection Technology Co., Ltd., Nanjing 210061, China
*Corresponding author
Abstract

Laser-induced breakdown spectroscopy (LIBS) is an emerging atomic spectroscopy technique that has the advantages of low sample pre-treatment and rapid, in situ, and simultaneous multi-element measurements. LIBS demonstrates good prospects in the field of coal analysis. In recent years, chemometric and machine learning models have been widely used to improve the quantitative accuracy of LIBS in coal analysis. Generally, these models rely on a certain number of training samples to ensure the reliability of the prediction results. However, obtaining the certified content (label information) of coal samples used for model training requires traditional chemical analysis, which is complex and time-consuming. This may lead to insufficient training samples and poor model performance. To tackle the small sample problem in LIBS-based coal analysis, this work proposes a semi-supervised learning method based on the ensemble of multiple models. 5 baseline models are first established based on the initial training set, including multiple linear regression (MLR), partial least squares regression (PLSR), locally weighted partial least squares regression (LW-PLSR), support vector regression (SVR), and kernel extreme learning machine (K-ELM). The unlabelled data are processed using the 5 models, and 5 prediction values are obtained. For each unlabelled sample, the standard deviation of the 5 prediction values is calculated, and the unlabelled sample corresponding to the smallest standard deviation is added to the training set. Its pseudo label is the average of the 5 prediction values. As the training set is iteratively expanded, its corresponding training model is updated. The final training model is optimized and used to analyse the test samples. The proposed method is tested on a coal dataset containing 20 training samples, 39 test samples and 280 unlabelled samples. The results show that the proposed method improves the coefficient of determination ( R2) for content prediction of fixed carbon, ash, and volatile by 0.033, 0.102 and 0.118, respectively. Therefore, if the number of training samples is insufficient, semi-supervised learning can effectively improve the accuracy and reliability of LIBS quantification.

Keyword: Laser-induced breakdown spectroscopy; Semi-supervised learning; Coal; Quantitative analysis
引言

煤炭是支撑我国国民经济和社会发展的重要基础能源, 在未来一段时期内仍将作为我国的主导能源。 在“双碳”背景下, 煤炭的清洁、 高效、 低碳利用对保障能源安全、 实现能源结构平稳转型发挥关键作用。 快速煤质分析是指对煤炭的灰分、 挥发分、 固定碳、 热值、 硫分等性能指标进行测量, 有利于提高煤炭利用效率、 确保煤电机组安全生产。 传统的煤质分析主要基于离线的化学分析, 需要人工采样、 制样、 检测等过程, 操作复杂且耗时长、 获取煤质信息滞后, 无法对煤炭燃烧和煤电机组运行提供实时指导[1]。 目前常用的煤质快速分析技术包括X 射线荧光光谱法(XRF)、 中子瞬发γ射线活化分析法(PGNAA)等[2]。 然而XRF法无法检测低原子序数的元素, PGNAA法存在辐射危害且维护成本高等问题。

激光诱导击穿光谱(LIBS)是一项新兴的原子发射光谱技术。 该技术采用高能脉冲激光激发样品产生等离子体, 并探测等离子体发射光谱中元素的特征谱线强度。 LIBS具有快速、 原位、 多元素同时分析等优势, 且无需复杂的样品预处理, 能够满足煤质快速分析的需求。 近年来, 基于LIBS技术的煤质分析系统通过完善制样、 测量来提升定量分析性能, 在电力行业得到示范应用[3]。 原煤经过制粉和压饼等处理, 以降低物理基体效应、 提高采样的代表性[4, 5]。 同时, 光束整形、 空间约束、 光谱联用等技术提高了光谱信号的稳定性[6, 7, 8], 优化对煤质的分析。 尽管如此, 较高的测量不确定性和测量误差制约了LIBS技术的精确定量化以及在煤质分析中大规模商业化[9]。

目前, 化学计量学和机器学习模型在提高LIBS对煤质分析的准确度方面发挥了重要作用。 线性模型如偏最小二乘回归(PLSR)、 最小绝对值收敛和选择算子(LASSO)能够有效地从高维光谱数据中提取重要的成分信息[10, 11], 非线性模型如支持向量回归(SVR)、 核极限学习机(K-ELM)、 卷积神经网络(CNN)能够有效地处理光谱强度与分析物含量之间的复杂关系[12, 13]。 化学计量学和机器学习模型通常需要一定数量的训练数据, 以确保分析结果的可靠性。 然而在实际的LIBS定量分析中, 获取煤样的真实的成分含量信息(标签)依赖于复杂、 耗时且昂贵的化学分析, 这导致训练集样本数不足、 模型性能下降。 迁移学习和半监督学习是常用于解决小样本问题的机器学习方法。 迁移学习使用源域中大量的有标签数据, 为不同但相关的目标域建立模型。 由于需要大量有标签的源域数据, 迁移学习尚未被广泛应用于LIBS定量分析。 半监督学习结合了监督学习和无监督学习, 能够同时使用少量的有标签数据和大量的无标签数据来进行定性、 定量分析。 例如, Wang等[14]采用LIBS对爆炸物与含有类似成分的塑料进行测量, 并基于K-最近邻(K-NN)算法建立半监督学习模型对数据分类, 取得了优于类比的软独立模型(SIMCA)的准确度。 Li等[15]基于最小二乘支持向量机(LS-SVM)和共同训练策略建立半监督的LIBS定量模型, 对高合金钢样品中的铬浓度进行分析, 其均方根误差低于PLSR和SVR。

针对基于LIBS技术的煤质分析, 大量的无标签光谱数据为无监督学习提供了应用条件。 本文利用LIBS结合半监督学习方法对煤样中的固定碳、 灰分、 挥发分含量进行预测。 本文提出了多模型集成的半监督学习方法, 通过分析无标签数据、 扩充训练集, 提高小样本条件下LIBS定量分析的准确度。

1 实验部分
1.1 样品与仪器

实验所用339份煤样收集于不同矿区和发电厂。 煤样经过研磨后的粒径小于0.2 mm, 每份样本中约3 g煤粉被压饼机(压力为20 t, 处理时间为10 s)制成直径为30 mm、 厚度为3 mm的表面光滑煤饼。 待测的煤质成分包括固定碳(%)、 灰分(%)、 挥发分(%), 预先由标准的化验分析获得(GB/T 212—214), 其含量的均值、 标准差、 最大值、 最小值如表1所示。

表1 煤质分析样本成分含量分布表 Table 1 Content distribution of samples for coal analysis

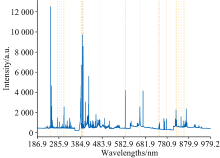
实验所用仪器为集成式LIBS系统(ChemReveal LIBS Desktop Elemental Analyzer 3766)。 激光光源为输出波长1 064 nm的Nd∶YAG激光器, 脉冲能量为90 mJ, 光谱积分时间为0.5 μs。 样品烧蚀产生的等离子体通过光纤收集到7通道光谱仪, 波长范围为186.87~979.23 nm, 光谱分辨率为0.09 nm。 为了降低信号不稳定性, 实验中每个样品在不同位置采集了176个光谱, 取平均值用于定量分析。 煤样的平均光谱如图1所示。 对于固定碳、 灰分、 挥发分含量分析, 结合NIST数据库, 信号较强的特征线包括C Ⅰ(247.86 nm)、 Ca Ⅱ(393.37 nm)、 Al Ⅰ(394.4 nm)、 N Ⅰ(821.63 nm)、 O Ⅰ(844.67 nm)等[16]。

图1 煤质分析样品平均光谱图Fig.1 Average spectrum of samples for coal analysis

1.2 建模方法

1.2.1 基线模型

本文采用的基线模型包括多元线性回归(MLR)、 PLSR、 局部加权偏最小二乘回归(LW-PLSR)、 SVR、 K-ELM。 MLR在多个自变量和单个因变量之间建立线性关系, 是常用于LIBS定量化的统计学方法。 PLSR是一种常用的统计分析方法, 用于处理多个自变量之间存在共线性或高度相关性的情况。 相较于传统的MLR, PLSR引入了潜在变量的概念, 通过最小化自变量与因变量之间的协方差来构建模型。 PLSR的核心思想是将原始自变量空间转换为潜在变量空间, 以降低变量间的相关性。 通过解决共线性问题, PLSR能够更加有效地分析自变量对因变量的影响。 LW-PLSR是PLSR的一种扩展形式, 它在建立模型时考虑了样本之间的权重差异。 对于每个训练样本, 根据其与待测样本之间的相似度, 赋予不同的权重, 该权重值决定了该样本对模型的贡献程度。 样本权重的计算通常基于核函数, 相似度越高的样本权重越高。 SVR通过在高维特征空间中搜索最佳的回归超平面并使结构风险最小化, 使误差控制在一定阈值内。 SVR通过引入核函数来实现非线性回归, 核函数能够将原始特征映射到高维空间, 使得原始非线性问题在高维空间中变为线性可分的问题。 极限学习机(ELM)是单隐含层前馈神经网络, 其输入权重随机生成。 K-ELM采用核函数替代隐含层的特征映射来提高ELM的稳定性。 此外, K-ELM模型还具有较快的训练速度和良好的泛化能力。

1.2.2 多模型集成的半监督学习

本工作提出多模型集成的半监督学习方法, 该方法包括初始训练、 数据更新、 模型测试三个步骤, 如图2所示。

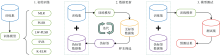图2 多模型集成半监督学习的流程图Fig.2 Flowchart of semi-supervised learning based on the ensemble of multiple models

(1) 初始训练: 根据训练集建立多个回归模型, 包括MLR、 PLSR、 LW-PLSR、 SVR、 K-ELM模型。 通过10折交叉验证, 确定每个模型的最优参数。

(2) 数据更新:

① 利用上面5种训练模型处理无标签数据, 得到该数据的5组预测值;

② 对于每个无标签样本, 计算其5个预测值的标准差;

③ 将最小标准差对应的无标签样本加入训练集, 并将其预测值的平均值作为伪标签;

④ 从无标签数据集中移除该样本, 并更新训练集和训练模型。

⑤ 重复①—④步骤, 直至将k个无标签样本加入训练集。

(3) 模型预测: 根据步骤(2)获得的数据集(训练集和伪标签数据集), 采用单独的回归方法建立模型。 通过10折交叉验证, 确定模型的最优参数。 利用该模型处理测试集样本, 得到预测结果。

2 结果与讨论
2.1 数据划分与预处理

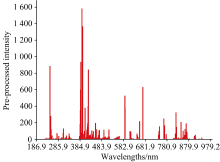
针对基于半监督学习的小样本数据分析, 总计339个煤样被随机划分为20个训练样本、 39个测试样本、 280个无标签样本。 为提高定量分析的准确度和避免模型过拟合, 原始光谱数据经过识别谱峰、 去除基线、 计算谱峰面积等预处理, 数据维数由12 990降为500。 首先, 识别原始光谱中强度最高的500个极大值位置, 并作为谱峰的中心波长。 然后, 对各谱峰连接中心波长紧邻的两个极小值位置, 作为谱峰基线, 计算基线上方的谱峰面积。 预处理后的平均光谱如图3所示。

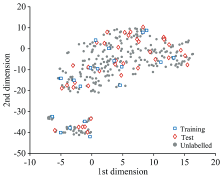
图3 预处理后的平均光谱Fig.3 Average spectrum after pre-processing

预处理后光谱数据经过t-分布随机近邻嵌入(t-SNE)降维处理, 所有样本在二维空间的分布和相似性如图4所示。 映射后的样本可分为两个聚类。 训练样本所占比例偏小(20/339), 与部分测试样本的距离相对较远。 因此训练模型的适用域无法很好地覆盖测试样本, 可能造成模型的预测结果欠佳。 而无标签样本所占比例极高(280/339), 其分布区域较好地覆盖了测试样本。

图4 t-SNE降维后LIBS数据的散点图Fig.4 The projected LIBS data using t-SNE

2.2 结果对比

本工作对比了半监督模型与基线模型在煤质分析任务上的准确度, 结果如表2所示。 半监督模型中引入无标签样本k的数量设置为50、 100、 150、 200、 250, 基线模型未采用无标签样本(k=0)。 MLR模型选取的谱线与文献[12]中一致。 针对测试样本的预测结果, 模型性能评价指标包括均方根误差(RMSE)和拟合系数(R2)。

表2 半监督学习模型和基线模型的预测结果比较(k为无标签样本数量) Table 2 Comparison of the prediction results of the semi-supervised learning model and the baseline models (k represents the number of unlabelled samples)

对于固定碳含量预测, 基线模型中K-ELM得到的RMSE最低, 为2.602。 横向对比, 半监督模型中基于K-ELM的预测结果多数优于基线K-ELM, 其中最小的RMSE为2.527 (k=150)。 其余的半监督模型在引入无标签样本后, 在大多数情况下优于对应的基线模型。 此外, 在引入较多数量的无标签样本后(k=200, 250), 半监督模型的性能无法进一步提升。 这表明, 采用远多于训练样本的无标签样本及其伪标签, 会使模型决策依赖于无标签样本及其伪标签, 导致定量分析可靠性降低。 对于灰分含量预测, MLR在基线模型中得到最低的RMSE, 为1.148。 而基于MLR的半监督模型在引入多于50个无标签样本后, 结果优于基线MLR, 其中最小的RMSE为1.045 (k=200)。 基于PLSR、 LW-PLSR、 SVR的半监督模型均展现出RMSE下降, 而基于K-ELM的半监督模型结果欠佳。 在该分析任务上, 半监督模型需引入较多的无标签样本(k>100)以提升性能。 对于挥发分含量预测, 基线模型中K-ELM得到最低的RMSE, 为1.316。 尽管基于K-ELM的半监督模型能够将RMSE降至1.285, 但基于LW-PLSR的半监督模型得到的RMSE最低, 为1.198 (k=50)。 除基于SVR的半监督模型外, 所有半监督模型都有效地降低了RMSE。

由上可见, 半监督学习在小样本情况下能够有效提升基于LIBS的煤质分析的准确度。 基线模型与半监督模型在煤质分析任务上的预测效果如图5所示, 固定碳、 灰分、 挥发分含量预测的R2分别从0.775、 0.404、 0.31上升为0.788、 0.506、 0.428, 对应的最佳模型分别为K-ELM (k=150)、 MLR (k=200)、 LW-PLSR (k=50)。 在15组横向对比(5个回归算法×3个分析任务)中, 13组半监督模型优于基线模型, 表明本文提出的方法在提高小样本LIBS数据定量分析准确度的同时, 具有较好的泛化能力。

图5 基线模型(上)与半监督学习模型(下)在煤质分析任务上的预测效果Fig.5 Prediction performance of baseline models (top) and semi-supervised learning model (bottom) on coal analysis tasks

3 结论

针对小样本问题, 提出了多模型集成的半监督学习方法, 并在基于LIBS的煤质分析数据上进行测试。 在训练样本数量不足的条件下, 该方法通过利用大量的无标签样本, 有效地提升LIBS定量化性能。 多模型集成的半监督学习方法将固定碳含量预测的RMSE从2.602降至2.527, 灰分含量预测的RMSE从1.148降至1.045, 挥发分含量预测的RMSE从1.316降至1.198。 该结果表明, 半监督学习是提升小样本LIBS数据定量分析性能的可行方案, 可以为相关LIBS应用提供一定的技术参考。

参考文献
[1] Sheta S, Afgan M S, Hou Z, et al. J. Anal. At. Spectrom. , 2019, 34(6): 1047. [本文引用:1]
[2] Dong M, Wei L, Lu J, et al. J. Anal. At. Spectrom. , 2019, 34(3): 480. [本文引用:1]
[3] Song W, Hou Z, Gu W, et al. Fuel. , 2021, 306: 121667. [本文引用:1]
[4] Redoglio D, Golinelli E, Musazzi S, et al. Spectrochim Acta Part B-At. Spectrosc. , 2016, 116: 46. [本文引用:1]
[5] Yao S, Xu J, Zhao J, et al. Energy & Fuels, 2017, 31(5): 4681. [本文引用:1]
[6] Hou Z, Afgan M S, Sheta S, et al. J. Anal. At. Spectrom. , 2020, 35(8): 1671. [本文引用:1]
[7] Wang Z, Hou Z, Lui S, et al. Opt. Express, 2012, 20(S6): A1011. [本文引用:1]
[8] Yao S, Qin H, Wang Q, et al. Spectrochim Acta Part A-Mol. Biomol. Spectrosc. , 2020, 239: 118492. [本文引用:1]
[9] Wang Z, Afgan M S, Gu W, et al. TrAC-Trends. Anal. Chem. , 2021, 143: 116385. [本文引用:1]
[10] Song W, Hou Z, Afgan M S, et al. J. Anal. At. Spectrom. , 2021, 36(1): 111. [本文引用:1]
[11] Li W, Dong M, Lu S, et al. Anal. Methods, 2019, 11(35): 4471. [本文引用:1]
[12] Song W, Afgan M S, Yun Y H, et al. Expert. Syst. Appl. , 2022, 205: 117756. [本文引用:2]
[13] Li L, Liu X, Yang F, et al. Spectrochim Acta Part B-At. Spectrosc. , 2021, 180: 106183. [本文引用:1]
[14] Wang Q, Teng G, Li C, et al. J. Hazard Mater. , 2019, 369: 423. [本文引用:1]
[15] Li X, Lu H, Yang J, et al. Plasma. Sci. Technol. , 2019, 21(3): 034015. [本文引用:1]
[16] Song W, Hou Z, Gu W, et al. Spectrochim Acta Part B-At. Spectrosc. , 2022, 195: 106490. [本文引用:1]