基于可见/近红外光谱和函数型线性回归模型的成熟期苹果可溶性固形物含量预测

引用本文

黄华, 刘亚, 马毅航, 向思函, 何佳宁, 王诗婷, 郭俊先. 基于可见/近红外光谱和函数型线性回归模型的成熟期苹果可溶性固形物含量预测[J]. 光谱学与光谱分析, 2024,44(7): 1905-1912.
HUANG Hua, LIU Ya, MA Yi-hang, XIANG Si-han, HE Jia-ning, WANG Shi-ting, GUO Jun-xian. Prediction of Soluble Solid Contents in Apples Using Vis-NIRS and Functional Linear Regression Model[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1905-1912.
Doi:10.3964/j.issn.1000-0593(2024)07-1905-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于可见/近红外光谱和函数型线性回归模型的成熟期苹果可溶性固形物含量预测

黄华¹, 刘亚², 马毅航¹, 向思函¹, 何佳宁¹, 王诗婷¹, 郭俊先^3,^*

1.新疆农业大学数理学院, 新疆乌鲁木齐 830052

2.新疆农业科学院综合试验场, 新疆乌鲁木齐 830013

3.新疆农业大学机电工程学院, 新疆乌鲁木齐 830052

*通讯作者 e-mail: junxianguo@163.com

作者简介: 黄华, 1981年生,新疆农业大学数理学院副教授 e-mail: 18899511151@163.com

收稿日期: 2023-04-01 修回日期: 2023-08-27

基金: 国家自然科学基金项目(61367001),新疆维吾尔自治区科技创新团队(天山创新团队)项目(2022TSYCTD0011),新疆农业大学2023年度自治区级大学生创新项目资助

摘要

可溶性固形物含量(SSC)是反映苹果品质和成熟度的重要指标, 能够用于苹果品质分析和成熟度预测。以新疆阿克苏冰糖心红富士苹果为研究对象, 从果实膨大定形期至完熟期, 以3 d等间隔周期采摘样本, 采集其380~1 110 nm的可见/近红外光谱, 测定其SSC, 共552个样品。然后, 利用基函数平滑方法将采集的可见/近红外光谱离散数据转化为光谱曲线, 即函数型数据, 并以可见/近红外光谱曲线、一阶导曲线、二阶导曲线为函数型解释变量, SSC为标量响应变量, 分别建立函数型线性回归模型。为了验证和分析模型的性能, 根据原始光谱离散数据, 经过移动平滑、一阶导和二阶导预处理后, 分别建立偏最小二乘回归(PLSR)、核支持向量机(KSVM)、随机森林(RF)、梯度提升树(GBM)和深度神经网络(DeepNN)。结果表明, 在建立的18个模型中, 针对训练集, PLSR-dNIR模型、 KSVM-dNIR模型、 RF-dNIR模型、 GBM-dNIR模型和Deep NN-d2NIR模型都优于FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型, 且Deep NN-dNIR模型最优( r_c=0.999 6,Rc2=0.998 6, RMSEC=0.074 0, RPDC=27.436 6); 针对测试集, FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型均优于其他所有模型, 且FunLR-NIR模型最优( r_v=0.953 4,Rv2=0.907 7, RMSEV=0.585 6, RPDV=3.301 7)。综合训练集和测试集的结果来看, 核支持向量机模型、随机森林模型、梯度提升树模型和深度神经网络模型容易过拟合, 而函数型线性回归模型具有更好的普适性。此外, 从三个函数型线性回归模型(FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型)的预测效果看, 模型均具有良好的鲁棒性和较高的预测精度。试验结果表明, 结合可见/近红外光谱技术与函数型数据分析构建的函数型线性回归模型, 可成功、有效地实现成熟期苹果的可溶性固形物含量预测。

关键词: 苹果; 可溶性固形物含量; 可见/近红外光谱; 函数型数据分析; 函数型线性回归模型

中图分类号:O657.3 文献标志码:A

Prediction of Soluble Solid Contents in Apples Using Vis-NIRS and Functional Linear Regression Model

HUANG Hua¹, LIU Ya², MA Yi-hang¹, XIANG Si-han¹, HE Jia-ning¹, WANG Shi-ting¹, GUO Jun-xian^3,^*

1. College of Mathematics and Physics, Xinjiang Agricultural University, Urumqi 830052, China

2. Comprehensive Testing Ground, Xinjiang Academy of Agricultural Sciences, Urumqi 830013, China

3. Mechanical and Traffic College, Xinjiang Agricultural University, Urumqi 830052, China

*Corresponding author

Abstract

Soluble solid contents (SSC) are an important indicator of apple quality and maturation and can be used for quality analysis and ripeness prediction. In this paper, 552 samples of Sugar Core Red Fuji apples from Aksu of Xinjiang Province were picked at equal intervals of three days from the fruit swelling and setting stage to the complete mature stage, the visible near-infrared spectroscopy (vis-NIRS) of the samples at 380 to 1 110 nm were collected respectively, and the SSC were measured. Then, the collected discrete data of vis-NIRS were transformed into spectral curves using the basis function smoothing method, i. e., function-type data, and respectively, the functional linear regression model was established with Vis-NIRS curves, first-order derivative curves, and second-order derivative curves as functional explanatory variables and SSC as scalar response variables. To confirm and analyze the performance of the model, partial least squares regression (PLSR), kernel support vector machine (KSVM), random forest (RF), gradient boosting tree (GBM) and deep neural network (DeepNN) were established by the original spectral discrete data after moving smooth, first-order derivative and second-order derivative pre-processing. The results show that among the 18 models, for the training set, the PLSR-dNIRmodel, KSVM-dNIR model, RF-dNIR model, GBM-dNIR model, and Deep NN-d2NIR model were outperformed the FunLR-NIR model, FunLR-dNIR model and FunLR-d2NIR model, and the Deep NN-d2NIR model was optimal ( r_c=0.999 6,Rc2=0.998 6, RMSEC=0.074 0, RPDC=27.436 6). For the test set, the FunLR-NIR model, FunLR-dNIR model, and FunLR-d2NIR model outperformed all other models, and the FunLR-NIR model was optimal ( r_v=0.953 4,Rv2=0.907, RMSEV=0.585 6, RPDV=3.301 7). The results of the training sets and test sets show that the kernel support vector machine model, random forest model, gradient boosting tree model, and deep neural network model are prone to overfitting. In contrast, the functional linear regression model has better generalizability. Besides, the prediction results of the three functional linear regression models (FunLR-NIR model, FunLR-dNIR model, and FunLR-d2NIR model) showed that all the models have good robustness and high prediction accuracy. The experimental results showed that the functional linear regression models combined with vis-NIR spectroscopy and functional data analysis could successfully and effectively achieve the prediction of soluble solid contents of apples at the ripening stage.

Keyword: Apple; Soluble solid content; Visible near-infrared spectroscopy; Functional data analysis; Functional linear regression model

文章图片

引言

苹果是一种常见的水果, 富含丰富的糖类、维生素和矿物质等营养物质, 营养价值高, 深受人们喜爱。苹果的成熟期是其生长的一个关键生命期, 是决定果实品质的关键生长期, 对水果的品质和市场价值具有关键作用^[1]。可溶性固形物含量(soluble solids content, SSC)是反映和决定水果品质和成熟度的主要指标之一, 测定SSC是农副产品加工和食品营养研究的基础问题^[2]。研究一种快速、准确、无损的SSC检测方法对监测苹果个体的品质和成熟状况, 指导苹果的采收后分级加工和提升苹果商品化效益具有重要意义和经济价值。

针对水果内部品质检测, 国内外比较常用的是近红外光谱技术, 它是利用可见/近红外光谱区光子与有机分子中的含氢官能团的倍频和合频吸收原理, 对被测物质进行定量和定性分析的一种现代、无损检测技术, 具有快速简便、无试剂、过程无污染、多组分同时测定等优点, 已广泛应用于农业、食品等领域^{[3, 4, 5]}。国内外学者利用可见/近红外光谱技术对苹果内部品质检测开展了大量的研究。在光谱采集模式方面, 使用漫反射、半透射、漫透射、拉曼光谱及多模式获取光谱信号, 用于检测苹果内部品质^{[6, 7]}。在SSC预测模型研究方面, 不同的光谱预处理方法, 结合不同的特征波长选择和特征提取算法, 研究建立主成分回归^[8]、偏最小二乘回归^{[9, 10, 11, 12, 13]}、支持向量机回归^[14]、机器学习^{[15, 16]}、神经网络^[17]、深度学习^[18]和集成学习^[19]等模型。从已有的研究可以发现, 利用可见/近红外光谱技术进行苹果品质检测研究多针对成熟采摘后的果实, 而对生长成熟期内苹果SSC的光谱无损检测研究较少。同时, 建立苹果SSC预测模型都是将可见/近红外光谱看作多变量进行建模, 没有充分考虑隐含在光谱曲线中的空间信息, 而将可见/近红外光谱看作连续曲线(或函数), 基于函数型数据分析思想建立苹果SSC预测模型鲜有研究报道。

基于此, 以成熟期内新疆阿克苏冰糖心红富士苹果为研究对象, 在等间隔采摘周期, 采摘一定数量的苹果, 采集苹果可见/近红外光谱数据, 测定SSC, 然后, 从函数型数据分析视角出发^[20], 将采集的可见/近红外光谱离散数据转化为函数型数据, 并以可见/近红外光谱曲线、一阶导曲线、二阶导曲线为函数型解释变量, SSC为标量响应变量, 分别建立苹果SSC的函数型线性回归预测模型, 以期提高模型的普适性、鲁棒性和预测精度, 为光谱技术在苹果成熟期大田管理、采摘期预测、内部多品质检测和成熟度判别等提供基础支撑。

1 实验部分

1.1 材料

试验区位于新疆阿克苏市红旗坡农场(41°15'N, 80°18'E), 试验样本选取新疆阿克苏冰糖心红富士苹果, 采摘和测定时间为2015年8月20日—10月30日, 该时段为苹果果实膨大定形期至果实成熟采收期。

试验中, 采摘的苹果样品均于当日在当地完成光谱采集和SSC测定。光谱采集设备选用美国海洋光学公司Maya2000Pro可见/近红外光纤光谱仪(波长范围198~1 118 nm, 波长点数2 068个, 光学分辨率0.035 nm, 采样间隔0.42 nm), 配以高能量连续宽波段HL-2000型20 W卤钨灯, 通过光纤连接光源与光谱仪, 将样品放置于支架的样品池中; 进行光谱采集前, 开机预热30 min, 之后在配套Ocean Options Spectra Suite采集软件上选择反射测量模式, 开启软件的电子暗噪声校正和杂散光校正, 用标准聚四氟乙烯漫反射白板为背景进行参考光谱校正和遮光方式进行暗场校正, 校正完成后采集光谱。采集环境参数: 室温(22± 2)℃, 湿度50%± 3%; 光谱采集参数: 平滑度3, 平均次数10, 波长范围: 380~1 110 nm。光谱采集点选取果实赤道面上120°均匀分布且无缺陷的3点, 每个测点采集3条光谱曲线, 取其平均光谱作为单个苹果的光谱曲线。

可溶性固形物含量测定选用ATAGO PR-101型数字折光仪(Tokyo, Japan, 精度± 0.1°Brix)。在完成光谱采集后, 按NY/T2637—2014《水果和蔬菜制品可溶性固形物的测定折射法》, 逐个测定每个样品的可溶性固形物含量。测定时, 分别剜取3个光谱采集点附近体积为15 mm×15 mm×15 mm的果肉组织(含果皮), 用榨汁器获取汁液, 滴于ATAGO PR-101型数字折光仪的样液池中, 测定苹果的可溶性固形物含量。每次使用榨汁器和数字折光仪前, 用纯净水和吸水纸清洗干净, 取3次测量的平均值作为单个苹果的可溶性固形物含量值。

1.2 方法

1.2.1 函数型数据预处理

函数型数据是指对定义在希尔伯特空间L²上的函数型随机变量X={X(t), t∈ T}进行n次具体实现所构成的数据集{x_i(t), i=1, 2, …, n}, 其中T=[a, b]是一个实值可测区间, 可以是时间区间, 也可以是其他变量, 比如波长区间。函数型数据的离散观测值可表示为{x_i(t_j), i=1, 2, …, n; j=1, 2, …, m}, 其中, x_i(t_j)表示函数型数据x_i(t)在网格点t_j∈ T处的实际观测值^[20]。

在函数型数据分析时, 首先需要对离散数据通过插值或平滑来重构隐含在数据中的本征函数。由于实测数据通常会有误差, 因此, 常常基于基函数系统(傅里叶基、样条基、径向基、小波基等), 利用平滑方法进行处理, 且通过最小二乘法或粗糙惩罚法等来估计基函数的对应系数。比如, 试验获取的每个苹果样品的可见/近红外光谱离散数据, 通过基函数平滑预处理, 则可获得该苹果样品的函数型数据, 也即是一条可见/近红外光谱曲线。

1.2.2 函数型线性回归模型

采用的函数型线性回归模型是一种自变量(解释变量)为函数型、响应变量(因变量)为标量的线性回归模型, 其表达式可表示为^{[21, 22, 23]}

$Y = \int_{T} X (t) β (t) d t + ε$ (1)

式(1)中, Y为标量响应变量; X(t), β (t)分别表示定义在连续区间T上的函数型解释变量和参数函数; ε 表示误差项。

响应变量是苹果可溶性固形物含量, 记作SSC, 函数型解释变量是可见/近红外光谱曲线、一阶导曲线、二阶导曲线, 分别记作NIR, dNIR, d2NIR, 连续区间T是波长区间, 仍用T表示。则建立如式(2)—式(4)几类函数型线性回归模型

$SSC = \int_{T} NIR (t) β (t) d t + ε$ (2)

$SSC = \int_{T} dNIR (t) β (t) d t + ε$ (3)

$SSC = \int_{T} d 2 NIR (t) β (t) d t + ε$ (4)

上述模型的参数函数均利用基于基函数展开的广义最小二乘法完成估计^{[24, 25, 26]}。

1.2.3 模型精度评价指标

利用训练集的相关系数r_c、判决系数 $R_{c}^{2}$ 、均方根误差RMSEC和相对分析误差RPDC, 测试集的相关系数r_v、判决系数 $R_{v}^{2}$ 、均方根误差RMSEV和相对分析误差RPDV来评价模型的性能。相关系数、判决系数、均方根误差和相对分析误差的计算公式如式(5)—式(8)

$r = \frac{\overset{n}{\sum_{i = 1}} (y_{ac t} - {\bar{y}}_{act}) (y_{pred} - {\bar{y}}_{pred})}{\sqrt[]{\overset{n}{\sum_{i = 1}} (y_{act} - {\bar{y}}_{act})^{2} (y_{pred} - {\bar{y}}_{pred})^{2}}}$ (5)

$R^{2} = 1 - \frac{\overset{n}{\sum_{i = 1}} (y_{act} - y_{pred})^{2}}{\overset{n}{\sum_{i = 1}} (y_{act} - {\bar{y}}_{act})^{2}}$ (6)

$RMSE = \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} (y_{act} - y_{pred})^{2}}$ (7)

$RPD = \frac{SD}{RMSE}$ (8)

式(5)—式(8)中, y_act为实测值; y_pred为预测值; ${\bar{y}}_{act}$ 为实测值的均值; ${\bar{y}}_{pred}$ 为预测值的均值; n为样本量; SD为样本标准差; 一般情况下, 若r大于0.9或R²大于0.8, 表示模型拟合效果或预测效果较好; 若RPD>2.0, 认为模型具有较高的可靠性, 能够用于模型分析。

2 结果与讨论

2.1 苹果SSC统计特征

试验实测23 d, 每天测定24个苹果, 共有552个苹果样品。样本的SSC均值± 标准差等于(13.333± 1.999)°Brix, SSC最小值等于8.8°Brix, 最大值等于19.4°Brix。按照7∶3的比例随机将苹果样本划分为训练集和测试集, 其中训练集的样本量为386, SSC范围为8.8~19.433 3°Brix, 均值± 标准差等于(13.324 4± 2.030 6)°Brix; 测试集的样本量为166, SSC范围为9~18.633 3°Brix, 其均值± 标准差等于(13.354 4± 1.933 4)°Brix, 表明训练集和测试集数据的分布良好。

2.2 可见/近红外光谱分析

在获取的苹果可见/近红外光谱离散数据基础上进行函数型数据分析时, 首先需要对离散数据进行平滑处理, 重构每个苹果样品的本征函数, 也即是转化为函数型光谱数据。

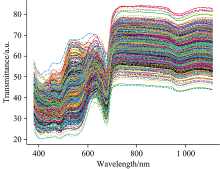
选取的基函数为B-样条基, 且norder等于4, breaks等于553, nbasis等于555。如图1所示, 为苹果样本的平均光谱散点图和对应的平滑曲线图。如图2所示, 为成熟期苹果样本预处理后的可见/近红外光谱曲线。从图形可以看出, 光谱曲线在380~1 110 nm范围内反射率值差异较大, 变化趋势基本一致, 呈现高—低—高—低—高的走势。

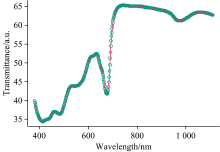	Figure Option View Download New Window
	图1 平均光谱散点图和对应的平滑曲线图Fig.1 The scatter plot of the average spectrum and the corresponding smoothed curve

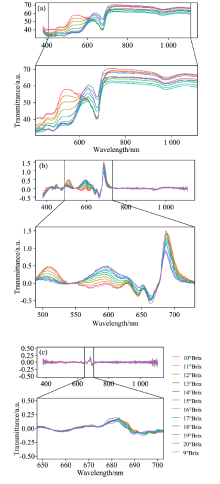
	Figure Option View Download New Window
	图2 苹果样本的可见/近红外光谱曲线Fig.2 Vis-NIRS curves of the apple samples

进一步, 基于原始光谱曲线及一阶导、二阶导曲线, 计算SSC的每个1°Brix所对应的平均光谱曲线, 并分析其与SSC之间的差异。如图3(a)所示, 不同SSC值对应的平均光谱曲线呈现比较明显的差异, 尤其是在440~1 110 nm波长范围; 如图3(b)所示, 基于一阶导曲线, 不同SSC值对应的平均光谱曲线, 在500~720 nm波长范围具有一定的差异; 如图3(c)所示, 基于二阶导曲线, 不同SSC值对应的平均光谱曲线, 在650~700 nm波长范围也具有一定的差异, 但不显著。

	Figure Option View Download New Window
	图3 每一度Brix变化所对应的原始(a)、一阶导(b)和二阶导(c)的光谱平均透射率Fig.3 Corresponding average transmittance of original (a), 1st derivative (b) and 2nd derivative (c) spectra for every change of one degree Brix (the bottom subplot is a local zoomed-in graph of the wavelength subinterval))

2.3 函数型线性回归模型

以苹果可溶性固形物含量SSC为响应变量, 以预处理后的可见/近红外光谱曲线NIR、一阶导曲线dNIR、二阶导曲线d2NIR为函数型解释变量, 分别建立函数型线性回归模型。建模过程中, 选取B-样条基作为参数函数和函数型解释变量的基函数, 且通过广义相关交叉验证(generalized correlated cross-validation, GCCV)来确定基函数的个数, 最后, 利用广义最小二乘法估计参数函数β (t)。

首先, 建立基于函数型变量NIR的函数型线性回归模型(简记为FunLR-NIR)。利用训练样本, 通过GCCV确定基函数的个数为52, 并基于GLS算法估计出参数函数β (t), 如图4(a)所示。可以看出, 波长范围555~635 nm所对应的|β |较大, 说明该波长区间的光谱对预测苹果SSC具有较大的效应和影响。

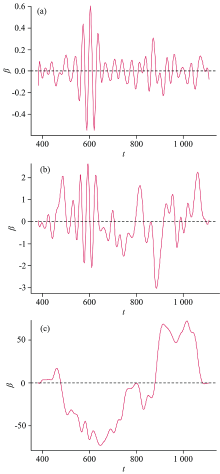	Figure Option View Download New Window
	图4 FunLR-NIR (a)、 FunLR-dNIR (b)、 FunLR-d2NIR (c)模型的参数函数β (t)估计Fig.4 Parameter function β (t) estimation for the FunLR-NIR (a), FunLR-dNIR (b), and FunLR-d2NIR (c) models

其次, 建立基于函数型变量dNIR的函数型线性回归模型(简记为FunLR-dNIR)。同样, 利用训练样本, 通过GCCV确定基函数的个数为51, 并基于GLS算法估计出参数函数β (t), 如图4(b)所示。可以看出, 在波长范围425~1 065 nm的一阶导光谱曲线对预测苹果SSC具有较大的效应和影响。

最后, 建立基于函数型变量d2NIR的函数型线性回归模型(简记为FunLR-d2NIR)。类似地, 利用训练样本, 通过GCCV确定基函数的个数为50, 并基于GLS算法估计出参数函数β (t), 如图4(c)所示。可以看出, 在波长范围450~1 065 nm的二阶导光谱曲线对预测苹果SSC具有较大的效应和影响。

2.4 模型精度分析

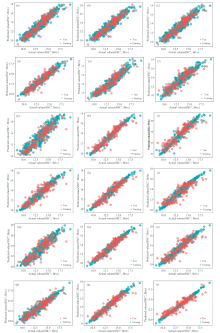
在完成函数型线性回归模型估计后, 将训练集和测试集分别代入FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型, 得出对应的SSC预测值, 如图5(a)—(c)所示, 分别为三个模型的SSC实测值与预测值的对比图。同时, 计算出训练集的r_c、 $R_{c}^{2}$ 、 RMSEC和RPDC, 测试集的r_v、 $R_{v}^{2}$ 、 RMSEV和RPDV, 见表1。此外, 便于模型对比分析, 基于原始光谱离散数据, 利用移动平滑、一阶导和二阶导方法进行预处理, 然后分别建立偏最小二乘回归(PLSR)、核支持向量机(KSVM)、随机森林(RF)、梯度提升树(GBM)和深度神经网络(DeepNN), 其对应的SSC实测值与预测值的对比图, 如图5(d)—(r)所示, 对应的r_c、 $R_{c}^{2}$ 、 RMSEC、 RPDC、 r_v、 $R_{v}^{2}$ 、 RMSEV和RPDV, 见表1。

Figure Option
View Download New Window

图5 不同模型的SSC实测值与预测值的对比图
(a)FunLM-NIR; (b): FunLM-dNIR; (c): FunLM-d2NIR; (d): PLSR-NIR; (e): PLSR-dNIR; (f): PLSR-d2NIR; (g)KSVM-NIR; (h): KSVM-dNIRl; (i): KSVM-d2NIR; (j): RF-NIR; (k): RF-dNIR; (l): RF-d2NIR; (m): GBM-NIR; (n): GBM-dNIR; (o): GBM-d2NIR; (p): DeepNN-NIR; (q): DeepNN-dNIR; (r): DeepNN-d2NIRFig.5 Comparison of the SSC actual values and SSC predicted values for different models
(a)FunLM-NIR; (b): FunLM-dNIR; (c): FunLM-d2NIR; (d): PLSR-NIR; (e): PLSR-dNIR; (f): PLSR-d2NIR; (g)KSVM-NIR; (h): KSVM-dNIRl; (i): KSVM-d2NIR; (j): RF-NIR; (k): RF-dNIR; (l): RF-d2NIR; (m): GBM-NIR; (n): GBM-dNIR; (o): GBM-d2NIR; (p): DeepNN-NIR; (q): DeepNN-dNIR; (r): DeepNN-d2NIR

表1 不同模型的SSC预测精度结果对比 Table 1 Comparison of SSC prediction accuracies of different models

模型	参数	训练集				测试集
模型	参数	r_c	$R_{c}^{2}$	RMSEC	RPDC	r_v	$R_{v}^{2}$	RMSEV	RPDV
FunLR-NIR	nbasis.x=52, nbasis.b=52	0.955 0	0.912 0	0.601 5	3.375 9	0.952 0	0.904 4	0.596 0	3.244 0
FunLR-dNIR	nbasis.x=51, nbasis.b=51	0.953 2	0.908 6	0.613 1	3.312 0	0.953 4	0.907 7	0.585 6	3.301 7
FunLR-d2NIR	nbasis.x=50, nbasis.b=50	0.951 8	0.906 0	0.621 8	3.265 6	0.951 1	0.902 9	0.600 7	3.218 4
PLSR-NIR	ncomp=30	0.975 8	0.949 7	0.443 8	4.576 0	0.928 5	0.859 7	0.739 8	2.613 6
PLSR-dNIR	ncomp=6	0.954 9	0.903 4	0.602 0	3.373 2	0.940 1	0.874 5	0.662 7	2.917 6
PLSR-d2NIR	ncomp=5	0.955 3	0.904 2	0.599 5	3.387 1	0.893 6	0.776 8	0.875 6	2.208 2
KSVM-NIR	kernel=“radial”, sigma=4.454 3×10^-3, C=1	0.937 0	0.841 1	0.716 3	2.834 8	0.910 4	0.768 8	0.813 9	2.375 6
KSVM-dNIR	kernel=“radial”, sigma=3.654 3×10^-3, C=1	0.934 2	0.833 0	0.731 4	2.776 3	0.913 8	0.778 9	0.798 6	2.421 1
KSVM-d2NIR	kernel=“radial”, sigma=9.947 6×10^-4, C=1	0.979 3	0.943 2	0.437 5	4.641 8	0.899 4	0.723 3	0.851 1	2.271 8
RF-NIR	mtry=33, ntree=600	0.982 6	0.952 4	0.403 5	5.032 6	0.886 4	0.713 0	0.893 3	2.164 4
RF-dNIR	mtry=33, ntree=600	0.987 8	0.966 4	0.342 4	5.929 9	0.930 1	0.829 1	0.712 0	2.715 3
RF-d2NIR	mtry=551, ntree=600	0.983 1	0.940 0	0.433 4	4.685 4	0.882 4	0.642 9	0.922 9	2.095 0
GBM-NIR	n.trees=150, interaction.depth=2	0.951 7	0.882 6	0.629 7	3.224 7	0.876 6	0.699 0	0.929 5	2.080 0
GBM-dNIR	n.trees=150, interaction.depth=3	0.994 3	0.987 7	0.219 4	9.255 5	0.940 4	0.872 6	0.657 6	2.940 1
GBM-d2NIR	n.trees=150, interaction.depth=3	0.982 1	0.957 1	0.393 1	5.165 4	0.889 8	0.742 2	0.879 8	2.197 4
DeepNN-NIR	hidden=c(200, 200), epochs=200	0.965 6	0.930 2	0.529 5	3.834 7	0.920 2	0.839 3	0.768 1	2.517 0
DeepNN-dNIR	hidden=c(200, 200), epochs=200	0.999 6	0.998 6	0.074 0	27.436 6	0.938 6	0.865 0	0.666 9	2.899 2
DeepNN-d2NIR	hidden=c(200, 200), epochs=200	0.999 2	0.998 3	0.082 5	24.600 4	0.925 9	0.823 5	0.729 8	2.649 4

表1 不同模型的SSC预测精度结果对比 Table 1 Comparison of SSC prediction accuracies of different models

结合表1和图5可知, 对于训练集而言, PLSR-dNIR模型、 KSVM-dNIR模型、 RF-dNIR模型、 GBM-dNIR模型和Deep NN-d2NIR模型都优于FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型, 且Deep NN-dNIR模型最优(r_c=0.999 6, $R_{c}^{2}$ =0.998 6, RMSEC=0.074 0, RPDC=27.436 6); 对于测试集而言, FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型均优于其他所有模型, 且FunLR-NIR模型最优(r_v=0.953 4, $R_{v}^{2}$ =0.907 7, RMSEV=0.585 6, RPDV=3.301 7)。综合训练集的拟合效果和测试集的预测性能来看, 核支持向量机模型、随机森林模型、梯度提升树模型和深度神经网络模型容易过拟合, 而函数型线性回归模型具有更好的普适性。

此外, 从三个函数型线性回归模型(FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型)可以看出, 以预处理后的可见/近红外光谱曲线NIR、一阶导曲线dNIR、二阶导曲线d2NIR为函数型解释变量, 建立的SSC函数型线性回归模型, 均具有良好的普适性、鲁棒性和较高的预测精度。综合上述分析结果表明, 结合可见/近红外光谱技术与函数型线性回归模型构建的成熟期苹果可溶性固形物预测模型具有可行性。

3 结论

结合可见/近红外光谱技术, 基于函数型数据分析的统计建模思想, 建立函数型线性回归模型, 实现新疆冰糖心红富士苹果的可溶性固形物含量估测, 得到如下主要结论:

(1)将采集的可见/近红外光谱离散数据转化为函数型数据, 能充分挖掘和利用隐含在光谱曲线中的空间信息, 对光谱回归建模具有重要价值;

(2)以可见/近红外光谱曲线、一阶导曲线、二阶导曲线为函数型解释变量建立的苹果SSC函数型线性回归模型。从参数函数估计结果得出, 基于FunLR-NIR模型, 波长区间555~635 nm的光谱对预测苹果SSC具有较大的效应和影响; 基于FunLR-dNIR模型, 波长范围425~1 065 nm的一阶导光谱曲线对预测苹果SSC具有较大的效应和影响; 基于FunLR-d2NIR模型, 波长范围450~1 065 nm的二阶导光谱曲线对预测苹果SSC具有较大的效应和影响;

(3)结合可见/近红外光谱, 建立了18个苹果SSC预测模型。结果表明, 训练集中, PLSR-dNIR模型、 KSVM-dNIR模型、 RF-dNIR模型、 GBM-dNIR模型和Deep NN-d2NIR牛型都优于FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型, 且Deep NN-d2NIR模型最优; 测试集中, FunLR-NIR模型、 FunLR-dNIR模型、 FunLR-d2NIR模型均优于其他所有模型, 且FunLR-NIR模型最优。综合来看, 核支持向量机模型、随机森林模型、梯度提升树模型和深度神经网络模型容易过拟合, 而函数型线性回归模型具有更好的普适性, 且三个函数型线性回归模型均具有良好的鲁棒性和较高的预测精度, 可成功、有效地实现成熟期苹果的可溶性固形物含量预测。

然而, 本工作建立的3个苹果SSC函数型线性回归模型, 并没有充分运用和融合函数型数据内部蕴含的曲线信息, 若将可见/近红外光谱曲线、一阶导曲线和二阶导曲线进行深度融合, 建立一个广义的函数型线性回归模型或集成学习模型是否更加有效, 是一个值得深入研究的问题; 此外, 从函数型线性回归模型的建模角度出发, 选择合适的波长区间也是一个值得关注的问题。

参考文献

文献列表

[1]	Pavlina D D, Georgios P. Scientia Horticulturae, 2011, 129(4): 752. [本文引用:1]
[2]	Patricia P, María-Teresa S, Dolores P, et al. Computers and Electronics in Agriculture, 2009, 69(1): 24. [本文引用:1]
[3]	Ma T, Xia Y, Inagaki T, et al. Postharvest Biology and Technology, 2021, 173: 111417. [本文引用:1]
[4]	Ma T, Zhao J, Inagaki T, et al. Postharvest Biology and Technology, 2022, 186: 111841. [本文引用:1]
[5]	Maii M N, Wang S, Mohamed A F. Trends in Food Science & Technology, 2022, 123: 290. [本文引用:1]
[6]	Olga M, Nils K A, Svein H K, et al. Postharvest Biology and Technology, 2021, 180: 111620. [本文引用:1]
[7]	LIU Yan-de, WANG Jun-zheng, JIANG Xiao-gang, et al(刘燕德, 王军政, 姜小刚, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(7): 2064. [本文引用:1]
[8]	MENG Qing-long, SHANG Jing, HUANG Ren-shuai, et al(孟庆龙, 尚静, 黄人帅, 等). Storage and Process(保鲜与加工), 2020, 20(5): 185. [本文引用:1]
[9]	Wang F, Zhao Y, Zheng J, et al. Computers and Electronics in Agriculture, 2021, 191: 106492. [本文引用:1]
[10]	RAO Li-bo, CHEN Xiao-yan, PANG Tao(饶利波, 陈晓燕, 庞涛). Chinese Journal of Luminescence(发光学报), 2019, 40(3): 389. [本文引用:1]
[11]	Guo Z, Wang M, Agyekum A A, et al. Journal of Food Engineering, 2020, 279: 109955. [本文引用:1]
[12]	Zhao X, Zhao X, Huang M. Chemometrics and Intelligent Laboratory Systems, 2021, 217: 104426. [本文引用:1]
[13]	Xia Y, Fan S, Li J, et al. Chemometrics and Intelligent Laboratory Systems, 2020, 201: 104017. [本文引用:1]
[14]	Zhang D, Xu Y, Huang W, et al. Infrared Physics & Technology, 2019, 98: 297. [本文引用:1]
[15]	Zhang M, Zhang B, Li H, et al. Infrared Physics & Technology, 2020, 111: 103529. [本文引用:1]
[16]	Lee A, Shim J, Kim B, et al. Journal of Food Engineering, 2022, 321: 110945. [本文引用:1]
[17]	Huang Y, Wang J, Li N, et al. Pattern Recognition Letters, 2021, 151: 76. [本文引用:1]
[18]	Bai Y, Xiong Y, Huang J, et al. Postharvest Biology and Technology, 2019, 156: 110943. [本文引用:1]
[19]	Tian X, Fan S, Li J, et al. Biosystems Engineering, 2020, 197: 64. [本文引用:1]
[20]	Ramsay J O, Silverman B W. Functional Data Analysis, 2nd ed. , New York: Springer, 2006. [本文引用:2]
[21]	Reiss P T, Ogden R T. Journal of the American Statistical Association, 2007, 102(479): 984. [本文引用:1]
[22]	Goldsmith J, Bobb J, Crainiceanu C, et al. Journal of Computational and Graphical Statistics, 2011, 20(4): 830. [本文引用:1]
[23]	Goldsmith J, Crainiceanu C, Caffo B, et al. Journal of the Royal Statistical Society Series C: Applied Statistics, 2012, 61(3): 453. [本文引用:1]
[24]	Febrero-Band e M, Oviedo de la Fuente M. Journal of Statistical Software, 2012, 51(4): 1. [本文引用:1]
[25]	McLean M W, Hooker G, Staicu A M, et al. Journal of Computational and Graphical Statistics, 2014, 23: 249. [本文引用:1]
[26]	Brockhaus S, Scheipl F, Hothorn T, et al. Statistical Modelling, 2015, 15: 279. [本文引用:1]

2011

0.0

... 苹果的成熟期是其生长的一个关键生命期, 是决定果实品质的关键生长期, 对水果的品质和市场价值具有关键作用^[1] ...

2009

0.0

... 可溶性固形物含量(soluble solids content, SSC)是反映和决定水果品质和成熟度的主要指标之一, 测定SSC是农副产品加工和食品营养研究的基础问题^[2] ...

2021

0.0

... 针对水果内部品质检测, 国内外比较常用的是近红外光谱技术, 它是利用可见/近红外光谱区光子与有机分子中的含氢官能团的倍频和合频吸收原理, 对被测物质进行定量和定性分析的一种现代、无损检测技术, 具有快速简便、无试剂、过程无污染、多组分同时测定等优点, 已广泛应用于农业、食品等领域^[3,4,5] ...

2022

0.0

2022

0.0

2021

0.0

... 在光谱采集模式方面, 使用漫反射、半透射、漫透射、拉曼光谱及多模式获取光谱信号, 用于检测苹果内部品质^[6,7] ...

2021

0.0

... 在光谱采集模式方面, 使用漫反射、半透射、漫透射、拉曼光谱及多模式获取光谱信号, 用于检测苹果内部品质^[6,7] ...

2020

0.0

... 在SSC预测模型研究方面, 不同的光谱预处理方法, 结合不同的特征波长选择和特征提取算法, 研究建立主成分回归^[8]、偏最小二乘回归^{[9,10,11,12,13]}、支持向量机回归^[14]、机器学习^[15,16]、神经网络^[17]、深度学习^[18]和集成学习^[19]等模型 ...

2021

0.0

2019

0.0

2020

0.0

2021

0.0

2020

0.0

2019

0.0

2020

0.0

2022

0.0

2021

0.0

2019

0.0

2020

0.0

2006

0.0

... 基于此, 以成熟期内新疆阿克苏冰糖心红富士苹果为研究对象, 在等间隔采摘周期, 采摘一定数量的苹果, 采集苹果可见/近红外光谱数据, 测定SSC, 然后, 从函数型数据分析视角出发^[20], 将采集的可见/近红外光谱离散数据转化为函数型数据, 并以可见/近红外光谱曲线、一阶导曲线、二阶导曲线为函数型解释变量, SSC为标量响应变量, 分别建立苹果SSC的函数型线性回归预测模型, 以期提高模型的普适性、鲁棒性和预测精度, 为光谱技术在苹果成熟期大田管理、采摘期预测、内部多品质检测和成熟度判别等提供基础支撑 ...

... T处的实际观测值^[20] ...

2007

0.0

... 采用的函数型线性回归模型是一种自变量(解释变量)为函数型、响应变量(因变量)为标量的线性回归模型, 其表达式可表示为^[21,22,23] ...

2011

0.0

... 采用的函数型线性回归模型是一种自变量(解释变量)为函数型、响应变量(因变量)为标量的线性回归模型, 其表达式可表示为^[21,22,23] ...

2012

0.0

... 采用的函数型线性回归模型是一种自变量(解释变量)为函数型、响应变量(因变量)为标量的线性回归模型, 其表达式可表示为^[21,22,23] ...

2012

0.0

... 上述模型的参数函数均利用基于基函数展开的广义最小二乘法完成估计^[24,25,26] ...

2014

0.0

... 上述模型的参数函数均利用基于基函数展开的广义最小二乘法完成估计^[24,25,26] ...

2015

0.0

... 上述模型的参数函数均利用基于基函数展开的广义最小二乘法完成估计^[24,25,26] ...