改进模糊推理分类器进行木材树种近红外光谱开集分类识别研究

引用本文

李振宇, 赵鹏, 王承琨. 改进模糊推理分类器进行木材树种近红外光谱开集分类识别研究[J]. 光谱学与光谱分析, 2024,44(7): 1868-1876.
LI Zhen-yu, ZHAO Peng, WANG Cheng-kun. Tree Class Recognition in Open Set Based on an Improved Fuzzy Reasoning Classifier[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1868-1876.
Doi:10.3964/j.issn.1000-0593(2024)07-1868-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

改进模糊推理分类器进行木材树种近红外光谱开集分类识别研究

李振宇¹, 赵鹏^1,^2,^*, 王承琨³

1.东北林业大学计算机与控制工程学院, 黑龙江哈尔滨 150040

2.广西科技大学计算机科学与技术学院(软件学院), 广西柳州 545006

3.黑龙江科技大学电子与信息工程学院, 黑龙江哈尔滨 150022

*通讯作者 e-mail: bit_zhao@aliyun.com

作者简介: 李振宇, 1988年生,东北林业大学计算机与控制工程学院博士研究生 e-mail: 271955032@qq.com

收稿日期: 2023-10-08 修回日期: 2024-01-10

基金: 国家自然科学基金地区基金项目(62265001),广西科技大学博士启动基金项目(校科博22Z07)资助

摘要

开集分类识别是近10多年来模式识别领域研究的热点, 它能够识别训练集中已知类别的测试样本, 同时还能够有效“拒识”未知类别的测试样本; 这些未知类别样本不包含在训练集中。现有的开集分类识别算法主要是基于Support Vector Machine(SVM)和深度学习网络框架进行改进, 并且主要应用在自然景物图像领域中; 在光谱分析领域中还鲜有报道。将传统的闭集框架下的模糊推理分类器进行模型改进, 提出了开集框架下的改进模糊推理分类器, 并将其应用到木材树种近红外光谱分类识别中。首先, 使用Flame-NIR近红外微型光谱仪采集木材样本横切面的近红外光谱曲线, 采用Metric Learning算法进行光谱向量维度约简降维至4维(4D)。其次, 改进闭集框架下的模糊推理分类器, 根据模糊规则置信度和各维度隶属度概率的乘积构建Generalized Basic Probability Assignment(GBPA), 再根据GBPA进行分类处理。在20个树种的具有不同的Openness指标下的近红外光谱数据集的分类识别对比实验表明, 改进的开集模糊推理分类器(fuzzy reasoning classifier in an open set, FRCOS)优于现有的基于机器学习和深度学习的开集分类识别主流算法, 具有较好的评价指标F-Score, Kappa系数及总体识别率。

关键词: 开集分类识别; 木材树种识别; 模糊推理分类器; 近红外光谱分析

中图分类号:O439 文献标志码:A

Tree Class Recognition in Open Set Based on an Improved Fuzzy Reasoning Classifier

LI Zhen-yu¹, ZHAO Peng^1,^2,^*, WANG Cheng-kun³

1. College of Computer and Control Engineering, Northeast Forestry University, Harbin 150040, China

2. School of Computer Science and Software Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China

3. School of Electronics and Information Engineering, Heilongjiang University of Science and Technology, Harbin 150022, China

*Corresponding author

Abstract

Open set recognition (OSR) has been investigated for approximately 10 years. It can recognize samples from the known classes in the training dataset, whereas it rejects samples from the unknown classes not included in the training dataset. The current OSR schemes are mainly based on Support Vector Machine (SVM) and deep learning neural networks. These OSR schemes are mainly used in natural scenery images and are rarely used in spectral analysis. In this paper, the classical fuzzy reasoning classifier in the closed set is improved with application to tree class spectral classification in the open set. First, a Flame-NIR spectrometer picks up the wood near-infrared (NIR) spectral curve. After metric learning processing, the spectral 4-dimensional (4D) feature vector is used as a classification feature. Second, the fuzzy reasoning classifier is improved for its use in an open set scenario. A new generalized basic probability assignment (GBPA) is used based on the confidence value of a fuzzy rule and the product of membership degree probability in each dimension. The comparison experimental results on wood NIR datasets with different “Openness”values indicate that our proposed scheme (Fuzzy Reasoning Classifier in an Open Set, FRCOS) outperforms the state of the art OSR schemes based on machine learning and deep learning with good performance evaluation measures.

Keyword: Open set recognition; Tree class recognition; Fuzzy reasoning classifier; Near-infrared spectral analysis

文章图片

引言

开集分类识别(open set recognition, OSR)是近10多年来模式识别领域的研究热点和难点, 因为它不仅要有效高精度分类处理已知类别, 而且还要有效“拒识”未知类别的样本。这些未知类别样本不包含在训练集中, 分类器训练时没有这些未知类别的任何先验知识。 Scheirer和Boult^[1]最早系统地开展了这方面的研究, 在单分类SVM的基础上提出了1-vs-Set Machine, 它在原来的单分类平面基础上, 又增加了一个平行的超平面, 定义了开放空间风险, 初步构建了用于OSR的SVM分类器。后来, 他们又提出了Compact Abating Probability (CAP)模型^[2], 特征空间中的点从已知类别区域移动到开放空间时, 该点的类别隶属度概率服从CAP模型。将CAP模型和统计学的极限值理论结合, 提出了Weibull校准的SVM (W-SVM), 进一步提高了OSR处理的精度。类似的, Jain等也使用了极限值理论建模决策界面处的正类训练样本, 提出了PI-SVM分类器^[3], 也采用了阈值分类策略。由于W-SVM和PI-SVM都采用了阈值策略来控制开放空间风险, 阈值选择成为了一个关键问题。

除了主流的基于SVM的OSR方法, Zhang和Patel提出了一种基于稀疏表示的OSR模型^[4]。该模型也使用极限值理论建模重建误差的拖尾分布, 因为该拖尾分布包括了用于OSR的重要信息。 Bendale和Boult扩展了Nearest Class Mean (NCM)分类器, 提出了用于OSR的Nearest Non-Outlier (NNO)算法^[5], 计算被测样本和各已知类别中心的距离, 作为已知类别分类和未知类别拒识的判定依据。另外, 该算法采用了Metric Learning进行特征选择降维, 它可以动态增加新的类别, 仍然使用以前的投影矩阵W。此外, Junior等还提出了最近邻分类器的开集版本^[6], 需要计算被测样本s到最近邻的两个不同类别的样本t, u的距离比值Ratio=d(s, t)/d(s, u)。如果Ratio≤T_R, 那么s就被分类到t所在的类别中; 否则, s就被拒识为未知类别。

随着深度学习网络的快速发展, 也提出了一些基于深度网络的OSR模型。 Bendale和Boult修改了深度网络中常见的SoftMax层, 将其替换为OpenMax层, 再次应用极限值理论和Weibull校准策略, 修正了已知类别和未知类别的隶属度概率, 用来指导被测样本分类^[7]。近几年, Generative Adversarial Nets (GAN)逐渐应用到OSR领域中, 主要归结为两大类方法。第一类方法是改进GAN中的目标函数和discriminator训练过程, 使用生成的已知类别和未知类别样本进行交替训练生成和判决过程。例如, Yang等就采用了这种策略进行人体动作识别的OSR研究^[8], 提出了一种OpenGAN深度网络模型。另一类方法是采用GAN系列网络生成未知类别的负类样本, 使用这些负类样本训练分类器例如OpenMax和SVM等, 从而得到更精准的分类界面, 有效分类已知的正类样本和未知的负类样本; 进一步提升OSR的分类精度^{[9, 10]}。上述的OSR研究主要应用在机器学习和机器视觉领域, 实验的图像数据集主要有字符及自然景物数据集等; 也用于人脸图像数据集中^{[11, 12]}。

另一方面, 光谱分析领域的OSR研究目前还少有报道, 主要集中于闭集框架下的不同物种及材料分类。例如, 木材样本的近红外光谱、太赫兹时域光谱及拉曼光谱被用于木材树种分类识别中^{[13, 14, 15]}。由于处理的是1D数据, 运算速度比较快。因此, 使用木材样本的光谱特征进行木材树种分类的OSR研究就很有意义。

模糊推理分类是模糊数学的一个分支, 它用于模式识别领域有以下特点。首先, 它具有较强的泛化能力, 可以用较小规模的训练集完成分类器的训练, 这点和深度学习网络的大规模训练集相比具有一定的优势。此外, 它比较适合于低维度向量(一般是4D~6D)的分类处理。例如, 传统的闭集框架下的模糊推理分类器曾经应用于木材颜色和缺陷的模糊分类系统中^{[16, 17, 18]}。综合这两点考虑, 模糊推理分类是比较适合于低维的光谱特征向量分类识别处理。此外, 经过大量文献调研, 发现基于模糊推理分类器的OSR研究还少有报道。因此, 本工作改进了闭集框架下的模糊推理分类器, 提出了开集框架下的改进模型, 并且将其应用于木材树种的近红外光谱分类进行实验验证, 取得了较好的效果; 证明了提出的开集框架下的改进模型的有效性。

1 光谱维度约简

使用的近红外光谱仪Flame-NIR spectrometer由美国海洋光学公司生产, 它采集的光谱区间为950~1 650 nm, 光谱分辨率为5.4 nm, 因此获取的光谱向量为128维(128D)。为了消除光谱向量各维度的冗余信息, 同时提高计算速度及降低计算复杂度, 一般需要对光谱向量做降维处理。常用的降维算法有Principal Component Analysis (PCA)和Linear Discriminant Analysis (LDA)等, 它们要求各类别数据符合正态分布, 应用有一定局限性。这里采用Mensink等提出的Metric Learning算法^[19], 该算法学习得到的投影矩阵W可以用于向量降维。另外, 正如作者所强调指出的^[19], 如果增加已知类别的数量, 那么该投影矩阵仍然可以继续使用, 具有很小的误差, 不需要重新进行训练和学习, 提高了向量降维的效率。因此, 选用了作者提出的k最近邻分类时使用的Metric Learning算法^[19], 简单说明如下, 定义3元组的hinge-loss如式(1)所示。

$L_{qpn} = [1 + d_{W} (x_{q}, x_{p}) - d_{W} (x_{q}, x_{n} {)]}_{+}$ (1)

式(1)中, [z]₊=max(0, z); d_W(x, x')=‖ Wx-Wx' $‖_{2}^{2}$ 。该3元组的hinge-loss为零, 如果负类样本x_n与查询样本x_q的距离至少比正类样本x_p与查询样本的距离多一个距离单位; 这里的x_n与x_q分别属于不同的类别, 而x_p与x_q来源于相同类别; 其他情况下的hinge-loss为正数。最终的学习目标函数为所有的3元组的hinge-loss的总和。这里的P_q, N_q分别表示查询样本x_q所对应的正类样本集合以及负类样本集合。

$L=\sum_{{x_{q}}}\sum_{{x_{p}\in P_{q}}}\sum_{{x_{n}\in N_{q}}}L_{qpn}$(2)

关于P_q的设计, 作者给出了两种方案。第一种方案是使P_q包括和x_q相同类别的所有样本, 此种情况下P_q和Metric Learning矩阵W无关。第二种方案是根据当前求得的W, 不断动态更新P_q, 使其包括和x_q相同类别的k个最近邻样本。由于W的不断更新计算, 导致产生的P_q集合也不断更新。

2 传统的闭集框架下的模糊推理分类器

本节简要介绍传统的闭集框架下的模糊推理分类器, 详细说明和解释可参考文献[20, 21]。在这种模糊分类系统中, 使用下面形式的if-then 模糊规则。

$\begin{array}{l} Rule R_{j} : If x_{i 1} is A_{j 1} and \dots x_{in} is A_{jn}; \\ Then Class D_{j} with C F_{j}, j = 1, 2, \dots, N_{rule} \end{array}$ (3)

这里的N_rule是总体的模糊规则数量; 训练样本为x_i=(x_i₁, x_i₂, …, x_in), i=1, 2, …, N_train(N_train表示训练集中的样本数量); A_j₁, …, A_jn是相应的模糊集, 分别对应于x_i₁, …, x_in; D_j是该规则产生的结果类别 (它是N_class个已知类别中的一个类别, 即D_j=C_i, i=1, 2, …, N_class); CF_j是模糊规则R_j的置信度。

2.1 模糊规则生成

训练样本集合x_i=(x_i₁, x_i₂, …, x_in), i=1, 2, …, N_train用于训练模糊分类器生成相应的模糊规则集合。某一条模糊规则R_j的D_j, CF_j经过下面的步骤确定。

(1) 对于类别h, 计算β _Class_h(j) (h=C_i, i=1, 2, …, N_class); μ_ji(·)是隶属度函数值, 它对应于模糊集A_ji。

$\begin{array}{l} β_{Class h} (j) = \sum_{x_{i}} μ_{j} (x_{i}), \\ μ_{j} (x_{i}) = μ_{j 1} (x_{i 1}) \dots μ_{jn} (x_{in}) \end{array}$ (4)

(2) 寻找类别 $\tilde{h}$ , 它具有最大值β _Class_h(j)。

$\begin{array}{l} β_{Class \tilde{h}} (j) = \max_{h = C_{i}} {β_{Class h} (j)}, \\ i = 1, 2, \dots, N_{class} \end{array}$ (5)

(3) 如果唯一的类别 $\tilde{h}$ 取得最大值(对应于模糊规则R_j), 那么令D_j= $\tilde{h}$ ; 同时相应的规则置信度CF_j按照式(6)和式(7)计算。

$C F_{j} = \frac{β_{Class \tilde{h}} (j) - \overset{̅}{β}}{\sum_{h} β_{Class h} (j)}$ (6)

$\bar{β} = \frac{\sum_{h} β_{Class h} (j)}{(N_{class} - 1)}$ (7)

2.2 模糊规则泛化

使用了2.1节的模糊规则生成过程以后, 可以获取N_rule个模糊if-then规则, 如式(3)所示。一个未知的测试样本x=(x₁, …, x_n)就可以用下面的两个步骤进行分类识别^{[20, 21]}(闭集框架下)。

(1) 计算α_Class_h(x), 对应于类别Class h。

$α_{Class h} (x) = \max {(μ_{j} (x) \cdot C F_{j} │ D_{j} = h)}$ (8)

(2) 寻找Class $\vec{h}$ , 它具有最大值α_Class_h(x); 这样x就被归类为Class $\vec{h}$ 。

$α_{Class \vec{h}} (x) = \max_{h = C_{i}} {α_{Class h} (x)}$ (9)

2.3 模糊规则矫正

模糊规则R_j的置信度CF_j可以进行矫正, 从而获得更高的分类精度。当某个样本被模糊规则R_j正确分类时, 我们强化该规则的置信度CF_j。相反的, 当某个样本被模糊规则R_j错误分类时, 相应的CF_j就需要降低, 具体计算参见式(10)和式(11)(此处的θ参数是一个正常数, 取值区间为[0, 1])。经过一轮的模糊规则矫正以后, 所有的训练样本都被处理了一次; 上述的矫正过程可能需要进行几轮迭代。

$\begin{array}{l} C F_{j}^{new} = C F_{j}^{old} - θC F_{j}^{old}, \\ 如果 x_{i} 被模糊规则 R_{j} 错误分类 \end{array}$ (10)

$\begin{array}{l} C F_{j}^{new} = C F_{j}^{old} + θ (1 - C F_{j}^{old}), \\ 如果 x_{i} 被模糊规则 R_{j} 正确分类 \end{array}$ (11)

3 改进的开集框架下的模糊推理分类器

在第2节闭集框架下, 训练样本集用来进行模糊规则生成及模糊规则矫正两个步骤, 从而产生模糊规则集Q。一般来说, 集合Q中的规则数量远远小于完备规则集U中的规则数量。集合U的规则数量为 $\overset{n}{\prod_{v = 1}} Card (T_{v}),$ 此处的n是特征向量的维度 $x_{i} = (x_{i 1}, x_{i 2}, \dots,$ $x_{in});$ 并且Card(T_v)表示第v个特征分量x_iv包括的隶属度函数的数量。对于一个未知的待测样本, 应用第2.2节的模糊规则泛化的两个步骤进行模式分类, 具体步骤参见式(8)和式(9)。

在开集框架下, 上面的模糊规则泛化步骤无法使用; 这里提出一种新颖的模糊规则泛化分类算法。它的具体实现步骤如下所述, 未知待测样本表示为x=(x₁, …, x₄), 因为原始的光谱向量应用Metric Learning进行特征降维至4D^[19]。

(1) 对于一条模糊规则R_j, 设其相应的模糊集为A_ji, i=1, 2, 3, 4。未知待测样本x=(x₁, …, x₄)对应于模糊集A_ji的相应概率计算如式(12)。

$\{\begin{array}{l} P_{x}^{A_{j 1}} = \frac{μ_{j 1} (x_{1})}{\overset{I}{\sum_{i = 1}} μ_{i} (x_{1})}, & 1 \leq i \leq I \\ P_{x}^{A_{j 2}} = \frac{μ_{j 2} (x_{2})}{\overset{L}{\sum_{l = 1}} μ_{i} (x_{2})}, & 1 \leq l \leq L \\ P_{x}^{A_{j 3}} = \frac{μ_{j 3} (x_{3})}{\overset{K}{\sum_{k = 1}} μ_{k} (x_{3})}, & 1 \leq k \leq K \\ P_{x}^{A_{j 4}} = \frac{μ_{j 4} (x_{4})}{\overset{D}{\sum_{d = 1}} μ_{d} (x_{4})}, & 1 \leq d \leq D \end{array}$ (12)

式(12)中, $I, L, K, D$ 分别表示特征分量 $x_{1}, \dots, x_{4}$ 的模糊集数量。这四个概率 $P_{x}^{A_{j 1}}, \dots, P_{x}^{A_{j 4}}$ 是彼此独立的, 满足条件 $\overset{I}{\sum_{j 1 = 1}} P_{x}^{A_{j 1}} = \overset{L}{\sum_{j 2 = 1}} P_{x}^{A_{j 2}} = \overset{K}{\sum_{j 3 = 1}} P_{x}^{A_{j 3}} = \overset{D}{\sum_{j 4 = 1}} P_{x}^{A_{j 4}} = 1$ 。

(2) 假设某条规则R_j具有置信度CF_j, 定义待测样本x属于这条规则的概率。

${P_{x}^{R_{j}}}^{=} P_{x}^{A_{j 1}} P_{x}^{A_{j 2}} P_{x}^{A_{j 3}} P_{x}^{A_{j 4}} C F_{j} = P^{R_{j}} (x) C F_{j}$ (13)

因此, 待测样本x属于某个已知类别C_i, i=1, 2, …, N_class的概率定义如式(14)

$α_{C_{i}} (x) = \max {(P_{x}^{R_{j}} │ D_{j} = C_{i})}$ (14)

(3) 定义待测样本x的GBPA如下, 参见式(15)。注意到每条模糊规则的决策类别D_j只能是一个类别C_i(一条模糊规则不能够同时产生两个及两个以上的类别), 因此有m{C₁, C₂, …, C_r}=0(r≤N_class)。

$\{\begin{array}{l} m {C_{i}} = α_{C_{i}} (x) \\ m {C_{1}, C_{2}, \dots, C_{r}} = 0 (r \leq N_{class}) \end{array}$ (15)

(4) 待测样本x属于未知类别的概率定义如式(16)(未知类别是指不包含在训练集中的类别)。

$m {ϕ} = 1 - \overset{N_{class}}{\sum_{i = 1}} m {C_{i}}$ (16)

(5) 对于待测样本 $x$ , 显然满足条件 $\sum_{U} P^{R_{j}} (x) = 1$ 和 $\sum_{Q} P^{R_{j}} (x) \leq 1$ , 因为Q是U的子集。此外, 由于 $C F_{j} \leq 1, \forall j$ , 所以有下面的结论 $\overset{N_{class}}{\sum_{i = 1}} m {C_{i}} \leq \sum_{Q} α_{C_{i}} (x) \leq \sum_{Q} P^{R_{j}} (x) \leq 1$ 。最后, 应用 $m {C_{i}} (i = 1, 2, \dots, N_{class})$ 和 $m {ϕ}$ 来预测待测样本x的类别; 最终的决策类别对应于 $\max (m {ϕ}, m {C_{i}}) (i = 1, 2, \dots, N_{class})$ 。如果 $m {ϕ}$ 取得最大值, 该待测样本 $x$ 判决为未知类别; 否则, 它判决为某个已知类别C_i。

例如, 木材树种数据集中包括20个树种类别, 选择其中的10个树种作为已知类别, 剩下的10个树种作为未知类别。这种情况下, 模糊规则集Q中的规则数量是318, 完备规则集U的规则数量是157 248。某个待测样本x使用上面的5个步骤进行处理, 从而求得各个类别的GBPA如表1所示。因此, 该待测样本判决为未知类别。此外, 图1给出了本算法FRCOS的整体流程图。

表1 计算求得的 GBPA, 对应于各个类别C_i(i=1, 2, …, 10)和ϕ Table 1 The computed GBPA corresponding to C_i (i=1, 2, …, 10) and ϕ

	Figure Option View Download New Window
	图1 改进的开集模糊推理分类器整体结构流程图Fig.1 The structure and flow graph of our revised FRCOS

4 实验结果与讨论

4.1 木材树种样本数据集

使用的数据集包括20个常见的木材树种, 这些木材树种包括针叶和阔叶树种两大类别。此外, 还包括一些相似树种, 分为视觉纹理相似树种和同属异种相似树种两大类别, 具体信息参见表2和图2。为避免木材样本同质化, 每个树种的板材购买于不同时期及不同市场, 保证每块板材来源于不同树木。经过加工处理后的木材样本为2 cm×2 cm×3 cm的小木块。采用Flame-NIR微型近红外光谱仪采集木材样本横切面的光谱反射率曲线, 采集的光谱曲线区间为950~1 650 nm, 光谱分辨率为5.4 nm, 获取的光谱向量为128D。每个树种包括50个训练样本, 因此总共采集了1 000条光谱曲线。需要说明一下, 木材光谱采集一般应该在相对稳定的实验室环境下进行, 实验室温度控制在(20± 2) ℃; 木材样本含水率控制在10%左右。具体的近红外光谱采集实验装置图参见图3。由于木材样本的横切面具有比较丰富的细胞组织和结构信息(例如管孔、木射线、薄壁组织等等), 因此采集的光谱曲线具有较多的模式可分性信息, 有利于后续的木材树种分类。相比较而言, 木材样本的径切面和弦切面所包含的分类信息较少。采集的20个木材树种样本的典型的近红外光谱曲线参见图4, 可以看出在区间950~1 650 nm, 这些光谱曲线具有一定的可分性信息(特别是在1 100和1 500 nm附近)。

表2 木材树种数据集(20个木材树种) Table 2 The used wood species dataset with 20 species

	Figure Option View Download New Window
	图2 20个木材树种样本横切面(具体顺序和表2中的序号相同)Fig.2 The cross sections of 20 wood species samples with an order as illustrated in Table 2

	Figure Option View Download New Window
	图3 木材样本光谱采集实验装置图 1: 卤素灯; 2: USB电缆; 3: 计算机; 4: 支架; 5: 微型光谱仪; 6: 光纤; 7: 样品; 8: Flame-NIR光谱仪Fig.3 The experimental setup of spectral acquisition of wood samples 1: Halogen lamp; 2: USB cable; 3: Computer; 4: Bracket; 5: Micro-spectrometer; 6: Optical Fiber; 7: Samples; 8: FlameNIR

	Figure Option View Download New Window
	图4 20种木材树种样本近红外光谱曲线Fig.4 The NIR spectral curves of 20 wood species samples

4.2 实验结果对比

模糊推理分类器的一个重要环节是特征向量x=(x₁, …, x₄)的各分量(各维度)的模糊数确定及隶属度函数的设计。前面已经说过, 这项工作一般只有经验丰富的专业人员, 才能够取得较好的效果。也正是因为此原因, 模糊推理分类器一般不适合于高维的特征向量分类任务, 此种情况下人为参与设计工作量很大。作为实例, 图5给出了x₁分量的模糊数及隶属度函数的优化确定及设计结果, 这里选取表2的前10个树种作为已知类别, 后10个树种作为未知类别。 x=(x₁, …, x₄)的各分量的模糊数为Card(T₁)=26, Card(T₂)=21, Card(T₃)=16, Card(T₄)=18。关于木材样本数据集中已知和未知类别的划分, 选取N_class个树种作为训练集中的已知类别(N_class=10, 5, 15, 18, 2); 剩下的树种作为测试集中的未知类别。此外, 对于已知类别, 应用留出法按照7∶3比例划分为训练样本和测试样本。例如, 当N_class=10时候, 总共有500个样本, 选取350个作为训练集, 剩下的150个放进测试集; 此外, 剩下的10个未知树种所有样本全部放进测试集。采用Scheirer等所定义的Openness来表示研究问题中涉及的已知类别和未知类别的相对比例(特征空间的开放程度)^{[1, 2]}, 具体公式定义如下。这样, 上述5种划分方法(N_class=10, 5, 15, 18, 2)的Openness分别计算为0.29, 0.5, 0.13, 0.05, 0.68。本文提出的新算法FRCOS是在Matlab R2021b编程环境下实现的。值得一提的是, 和主流的OSR算法不同^{[1, 2, 3, 5, 6, 7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本)。实际上, 判决阈值的优化选择比较困难, 经常会随着不同类别的数据集而发生改变。本算法是通过计算m{C_i}和m{ϕ }的最大值来实现分类判决, 巧妙地回避了阈值选择这个难点。

$Openness = 1 - \sqrt[]{\frac{| training classes |}{| testing classes |}}$ (17)

	Figure Option View Download New Window
	图5 x₁特征分量的隶属度函数优化设计Fig.5 The optimal design of membership function for the feature x₁

对比实验选取了5种代表性的OSR算法。第一种算法是Weighted Support Vector Data Description (Weighted-SVDD)^[22], 分类过程有两步骤。首先, 经过光谱维度约简以后, 使用Weighted-SVDD进行单类分类, 将待测样本分类成已知类别和未知类别两大类; 参数值为σ =0.1, C=0.75。其次, 对于已知类别, 再使用LibSVM进一步细分为某个具体的树种类别; 参数值为σ =10, C=2.5。它们都使用了Radial Basis Function (RBF)核函数。第二种算法是第1节引言中提到的Junior等提出的最近邻分类器的开集版本(open set version of nearest neighbor classifier, OSNN)^[6], 阈值参数T_R=0.8。这两种算法都使用了第1节的Metric Learning算法^[19]进行光谱维度约简。

第三种和第四种算法是扩展了基于Metric Learning算法^[19]的k最近邻分类器, 具体有3个步骤(这两种算法简称为Metric Learning Cluster (MLC)算法)。首先, 应用原始的Metric Learning算法进行光谱维度约简。其次, 使用密度峰值聚类算法^[23]对于训练集中的各类别样本进行聚类。其中, 第三种算法是通过聚类得到各类别的单个聚类中心; 第四种算法是通过聚类得到各类别的4个子聚类中心(相当于将训练集中的各个类别进一步划分成4个子聚类)。再者, 计算待测样本到训练集中的各类别的聚类中心或者子聚类中心的距离。在第三种算法, 设求得的最近距离为d₁<T₁, 那么该待测样本判决为相应的已知类别; 否则就拒识为未知类别。在第四种算法, 设求得的最近距离为d₂<T₂, 同样做类似判决处理。此处的距离阈值为T₁=0.2, T₂=0.1, 通过网格搜索法求得优化后取值。以上这四种算法都使用了木材树种的近红外光谱数据集。

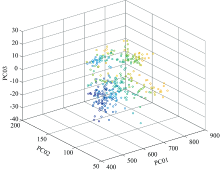
第五种算法采用了深度学习的OSR模型即OpenMax深度网络^[7], 这里的OpenMax网络采用ResNet50作为骨干网络。由于深度网络主要应用在图像领域中, 为了保证算法对比的客观性, 这里采用了木材树种横切面的可见光图像数据集。为此, 搭建了相应的图像采集实验装置, 如图6所示; 主要包括CCD摄像头, LED照明光源及光学显微镜(放大倍率10~100)。采集的原始图像尺寸为1280×960, 相应的放大倍率是50, 然后该图像被裁剪为960×960, 最终压缩为224×224。本方法和这5种算法的对比结果参见图7, 采用的分类识别评价指标为F-Score, Kappa系数以及Overall Recognition Accuracy (ORA)。此外, 还对比了两种经典的用于不同物种和材料分类的光谱分类方法。在这两种方法中, 光谱维度约简使用了PCA算法, 分类器使用了SVM和k最近邻分类器(k-Nearest Neighbor classifier, KNN, 参数k=5), 具体实验结果也参见图7。图8还给出了木材树种样本的光谱特征向量的散点图。各对比算法的时间复杂度及单次运行时间的比较参见表3, 本实验使用的硬件配置参数参见表4。

	Figure Option View Download New Window
	图6 木材树种横切面可见光图像采集实验装置图Fig.6 The experimental setup of visible image of wood cross sections

	Figure Option View Download New Window
	图7 实验结果对比 (a): F-Score vs. Openness; (b): ORA vs. Openness; (c): Kappa系数vs. OpennessFig.7 Experimental result comparisons (a): F-Score vs. Openness; (b): ORA vs. Openness; (c): Kappa coefficient vs. Openness

	Figure Option View Download New Window
	图8 木材树种样本光谱特征向量的散点图(10个已知树种)Fig.8 Scatter graph of wood species sample’ s spectral feature vectors

表3 算法时间复杂度及单次运行时间比较 Table 3 Comparisons of algorithmic time complexity and single running time

算法名称	时间复杂度	单次运行时间/ms
FRCOS	O(n²)	2.23
MLC(1 Center)	O(n²)	0.57
MLC(4 Center)	O(n²)	0.64
OSNN	O(n²)	2.29
Weighted-SVDD	O(n³)	2.61
OpenMax	$O (n \overset{D}{\sum_{l}} P^{2} K^{2} C_{l - 1} C_{l})$	22.99
PCA-SVM	O(n³)	1.27
PCA-KNN	O(n×d)	0.52

表3 算法时间复杂度及单次运行时间比较 Table 3 Comparisons of algorithmic time complexity and single running time

表4 硬件配置表 Table 4 Computer hardware configurations

OSNN算法的运行时间集中在计算欧氏距离。 Weighted-SVDD算法的运行时间主要包括两个部分, 分别是前端Weighted-SVDD单类分类和后端SVM多类分类, 这两个算法的时间复杂度均为O(n³), 单类分类单次运行耗时约为1.35 ms, 多类分类单次耗时约1.26 ms。 OpenMax算法的运行时间主要集中在骨干网络, 本工作使用的骨干网络为Res-Net-50, 其时间复杂度为 $O (n \overset{D}{\sum_{l = 1}} P^{2} K^{2} C_{l - 1} C_{l}), n$ 为样本数, D为网络的卷积层数, l为第l个卷积层, P为卷积核输出特征图的边长, K为卷积核的边长, C_l为网络第l层的输出通道数。由于OpenMax算法使用图像样本, 因此其耗时较高。 PCA-SVM算法的运行时间主要集中在SVM, 其时间复杂度为O(n³)。 PCA-KNN算法的运行时间主要集中在KNN算法上, 其时间复杂度为O(n×d), 其中d是特征维度。操作系统为Windows 11, 编程软件Matlab R2021b, 硬件配置如表4所示。

4.3 实验结果分析

从图7可以看出, 本方法实验结果都优于其他7种对比性算法, 据我们分析, 主要基于以下两点原因。首先, 模糊规则分类机制保证了OSR较高的分类精度。例如, 对于本工作的20种木材树种光谱数据集, 选取10种作为已知类别, 其余10种作为未知类别。此种情况下, 模糊规则集Q包括的规则数量是318, 而完备规则集U的规则数量是157 248。也就是说, 已知类别树种样本对应于模糊规则集Q中的318条规则, 而未知类别树种样本则对应于U\Q中的156 930条规则, 它给未知类别样本预留了很大的模糊规则空间, 从而保证了OSR的模糊规则分类精度。另外, 本实验采集的近红外光谱曲线为128D向量, 它经过Metric Learning光谱降维可以约简到4D。一般来说, 低维度向量(一般是4D~6D)适合于模糊规则的分类处理。高维度向量将导致各维度的模糊数确定和隶属度函数设计过于复杂, 并且模糊规则集Q和完备规则集U中的模糊规则数量呈指数增长, 导致过高的计算复杂度。

5 结论

改进了闭集框架下的模糊推理分类器, 提出了一种开集框架下的模糊推理分类器, 它适用于低维度的特征向量(一般是4D~6D)的OSR分类任务。进一步, 本工作的OSR的模糊推理分类器应用于木材树种近红外光谱数据集, 取得了较高的分类精度, 优于一些主流的OSR的机器学习和深度学习算法。这表明, OSR的模糊推理分类器是比较适合于低维度的光谱特征向量分类处理。本工作只是改进了传统的模糊推理分类器进行OSR分类处理, 近些年模糊推理分类领域出现了一些新的研究模型例如层次化的模糊推理分类模型和模糊关联规则分类模型等, 后期准备改进这些较新的模型应用于OSR领域中。

参考文献

文献列表

[1]	Scheirer W J, Rocha A D R, Sapkota A, et al. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(7): 1757. [本文引用:3]
[2]	Scheirer W J, Jain L P, Boult T E. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11): 2317. [本文引用:3]
[3]	Jain L P, Scheirer W J, Boult T E. Multi-Class Open Set Recognition Using Probability of Inclusion. In Computer Vision—ECCV 2014. Springer, 2014. 393. [本文引用:2]
[4]	Zhang H, Patel V. IEEE Trans Pattern Analysis and Machine Intelligence, 2017, 39(8): 1690. [本文引用:1]
[5]	Bendale A, Boult T E. Towards Open World Recognition. Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR), 2015. 1893. [本文引用:2]
[6]	Junior P R M, Souza R M D, Werneck R D O, et al. Machine Learning, 2017, 106(3): 359. [本文引用:3]
[7]	Bendale A, Boult T E. Towards Open Set Deep Networks. Proceedings of IEEE CVPR, 2016. 1563. [本文引用:3]
[8]	Yang Y, Chun P H, Yue L, et al. Pattern Recognition, 2019, 85: 60. [本文引用:1]
[9]	Ge Z Y, Demyanov S, Chen Z, et al. arXiv, 2017, 1707: 07418. [本文引用:1]
[10]	Geng C X, Huang S J, Chen S C. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(10): 3614. [本文引用:1]
[11]	Deng J, Dong W, Socher R, et al. ImageNet: A Large-scale Hierarchical Image Database. Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition, 2009. 248. [本文引用:1]
[12]	Russakovsky O, Deng J, Su H, et al. International Journal of Computer Vision, 2015, 115(3): 211. [本文引用:1]
[13]	Lavine B K, Davidson C E, Moores A J, et al. Applied Spectroscopy, 2001, 55(8): 960. [本文引用:1]
[14]	WANG Yuan, ZHE Shuai, ZHOU Nan, et al(王远, 折帅, 周南, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(9): 2719. [本文引用:1]
[15]	Ma T, Inagaki T, Tsuchikawa S. Holzforschung, 2021, 75(5): 419. [本文引用:1]
[16]	Bombardier V, Mazaud C, Lhoste P, et al. Computers in Industry, 2007, 58: 355. [本文引用:1]
[17]	Bombardier V, Schmitt E. Engineering Applications of Artificial Intelligence, 2010, 23: 978. [本文引用:1]
[18]	Bombardier V, Schmitt E, Charpentier P. Measurement, 2009, 42(2): 189. [本文引用:1]
[19]	Mensink T, Verbeek J, Perronnin F, et al. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2624. [本文引用:6]
[20]	Nakashima T, Schaefer G, Yokota Y, et al. Fuzzy Sets and Systems, 2007, 158: 284. [本文引用:2]
[21]	Ishibuchi H, Nakashima T. IEEE Transactions on Industrial Electronics, 1999, 46(6): 1057. [本文引用:2]
[22]	Tax D M J, Duin R P W. Machine Learning, 2004, 54(1): 45. [本文引用:1]
[23]	Rodriguez A, Alessand ro L. Science, 2014, 344(6191): 1492. [本文引用:1]

2013

0.0

... Scheirer和Boult^[1]最早系统地开展了这方面的研究, 在单分类SVM的基础上提出了1-vs-Set Machine, 它在原来的单分类平面基础上, 又增加了一个平行的超平面, 定义了开放空间风险, 初步构建了用于OSR的SVM分类器 ...

... 采用Scheirer等所定义的Openness来表示研究问题中涉及的已知类别和未知类别的相对比例(特征空间的开放程度)^[1,2], 具体公式定义如下 ...

... 值得一提的是, 和主流的OSR算法不同^{[1,2,3, 5,6,7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本) ...

2014

0.0

... 后来, 他们又提出了Compact Abating Probability (CAP)模型^[2], 特征空间中的点从已知类别区域移动到开放空间时, 该点的类别隶属度概率服从CAP模型 ...

... 采用Scheirer等所定义的Openness来表示研究问题中涉及的已知类别和未知类别的相对比例(特征空间的开放程度)^[1,2], 具体公式定义如下 ...

... 值得一提的是, 和主流的OSR算法不同^{[1,2,3, 5,6,7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本) ...

2014

0.0

... 类似的, Jain等也使用了极限值理论建模决策界面处的正类训练样本, 提出了PI-SVM分类器^[3], 也采用了阈值分类策略 ...

... 值得一提的是, 和主流的OSR算法不同^{[1,2,3, 5,6,7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本) ...

2017

0.0

... 除了主流的基于SVM的OSR方法, Zhang和Patel提出了一种基于稀疏表示的OSR模型^[4] ...

2015

0.0

... Bendale和Boult扩展了Nearest Class Mean (NCM)分类器, 提出了用于OSR的Nearest Non-Outlier (NNO)算法^[5], 计算被测样本和各已知类别中心的距离, 作为已知类别分类和未知类别拒识的判定依据 ...

... 值得一提的是, 和主流的OSR算法不同^{[1,2,3, 5,6,7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本) ...

2017

0.0

... 此外, Junior等还提出了最近邻分类器的开集版本^[6], 需要计算被测样本s到最近邻的两个不同类别的样本t, u的距离比值Ratio=d(s, t)/d(s, u) ...

... 值得一提的是, 和主流的OSR算法不同^{[1,2,3, 5,6,7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本) ...

... 第二种算法是第1节引言中提到的Junior等提出的最近邻分类器的开集版本(open set version of nearest neighbor classifier, OSNN)^[6], 阈值参数T_R=0 ...

2016

0.0

... Bendale和Boult修改了深度网络中常见的SoftMax层, 将其替换为OpenMax层, 再次应用极限值理论和Weibull校准策略, 修正了已知类别和未知类别的隶属度概率, 用来指导被测样本分类^[7] ...

... 值得一提的是, 和主流的OSR算法不同^{[1,2,3, 5,6,7]}, 本算法没有采用阈值策略来控制开放空间风险(也即判决未知类别样本) ...

... 第五种算法采用了深度学习的OSR模型即OpenMax深度网络^[7], 这里的OpenMax网络采用ResNet50作为骨干网络 ...

2019

0.0

... 例如, Yang等就采用了这种策略进行人体动作识别的OSR研究^[8], 提出了一种OpenGAN深度网络模型 ...

2017

0.0

... 进一步提升OSR的分类精度^[9,10] ...

2021

0.0

... 进一步提升OSR的分类精度^[9,10] ...

2009

0.0

... 也用于人脸图像数据集中^[11,12] ...

2015

0.0

... 也用于人脸图像数据集中^[11,12] ...

2001

0.0

... 例如, 木材样本的近红外光谱、太赫兹时域光谱及拉曼光谱被用于木材树种分类识别中^[13,14,15] ...

2019

0.0

... 例如, 木材样本的近红外光谱、太赫兹时域光谱及拉曼光谱被用于木材树种分类识别中^[13,14,15] ...

2021

0.0

... 例如, 木材样本的近红外光谱、太赫兹时域光谱及拉曼光谱被用于木材树种分类识别中^[13,14,15] ...

2007

0.0

... 例如, 传统的闭集框架下的模糊推理分类器曾经应用于木材颜色和缺陷的模糊分类系统中^[16,17,18] ...

2010

0.0

... 例如, 传统的闭集框架下的模糊推理分类器曾经应用于木材颜色和缺陷的模糊分类系统中^[16,17,18] ...

2009

0.0

... 例如, 传统的闭集框架下的模糊推理分类器曾经应用于木材颜色和缺陷的模糊分类系统中^[16,17,18] ...

2013

0.0

... 这里采用Mensink等提出的Metric Learning算法^[19], 该算法学习得到的投影矩阵W可以用于向量降维 ...

... 另外, 正如作者所强调指出的^[19], 如果增加已知类别的数量, 那么该投影矩阵仍然可以继续使用, 具有很小的误差, 不需要重新进行训练和学习, 提高了向量降维的效率 ...

... 因此, 选用了作者提出的k最近邻分类时使用的Metric Learning算法^[19], 简单说明如下, 定义3元组的hinge-loss如式(1)所示 ...

... 它的具体实现步骤如下所述, 未知待测样本表示为x=(x₁, …, x₄), 因为原始的光谱向量应用Metric Learning进行特征降维至4D^[19] ...

... 这两种算法都使用了第1节的Metric Learning算法^[19]进行光谱维度约简 ...

... 第三种和第四种算法是扩展了基于Metric Learning算法^[19]的k最近邻分类器, 具体有3个步骤(这两种算法简称为Metric Learning Cluster (MLC)算法) ...

2007

0.0

... 2 传统的闭集框架下的模糊推理分类器本节简要介绍传统的闭集框架下的模糊推理分类器, 详细说明和解释可参考文献[20,21] ...

... 一个未知的测试样本x=(x₁, …, x_n)就可以用下面的两个步骤进行分类识别^[20,21](闭集框架下) ...

1999

0.0

... 2 传统的闭集框架下的模糊推理分类器本节简要介绍传统的闭集框架下的模糊推理分类器, 详细说明和解释可参考文献[20,21] ...

... 一个未知的测试样本x=(x₁, …, x_n)就可以用下面的两个步骤进行分类识别^[20,21](闭集框架下) ...

2004

0.0

... 第一种算法是Weighted Support Vector Data Description (Weighted-SVDD)^[22], 分类过程有两步骤 ...

2014

0.0

... 其次, 使用密度峰值聚类算法^[23]对于训练集中的各类别样本进行聚类 ...