太赫兹多维度相位调控反射超表面研究

引用本文

黄若彤, 李九生. 太赫兹多维度相位调控反射超表面研究[J]. 光谱学与光谱分析, 2024,44(7): 1858-1867.
HUANG Ruo-tong, LI Jiu-sheng. Terahertz Multi-Dimensional Phase Regulated Reflection Coding Metasurface[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1858-1867.
Doi:10.3964/j.issn.1000-0593(2024)07-1858-10 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

太赫兹多维度相位调控反射超表面研究

黄若彤, 李九生^*

中国计量大学太赫兹研究所, 浙江杭州 310018

*通讯作者 e-mail: lijsh2008@126.com

作者简介: 黄若彤,女, 1998年生,中国计量大学太赫兹研究所硕士研究生 e-mail: 1452972370@qq.com

收稿日期: 2022-12-29 修回日期: 2023-09-18

基金: 国家自然科学基金项目(61871355, 61831012),浙江省科技厅人才工程项目(2018R52043),浙江省重点研发项目(2021C03153, 2022C03166)资助

摘要

数字编码超表面可以控制电磁波传输, 受到了广泛关注。大多数报道的编码超表面基于几何相位或传输相位实现对反射或者透射线极化波和圆极化波的2π相位覆盖, 限制了太赫兹波调控灵活性。提出传输相位和几何相位相结合排布超表面, 在线极化太赫兹波入射下, 基于传输相位机理设计的超表面产生了涡旋波束。根据几何相位原理, 在圆极化太赫兹波入射下, 设计的超表面产生了反射波束的偏转, 超表面可以在多个频点产生涡旋波束, 在0.9和1.2 THz处产生拓扑荷数 l=1和 l=2的涡旋波束, 通过卷积生成偏折涡旋波束。最后设计聚焦超表面, 实现了反射聚焦。研究结果表明, 设计的超表面提供了一种多自由度的太赫兹波偏振和相位操控方法, 在太赫兹系统具有广阔的应用潜力。

关键词: 太赫兹; 相位调控; 涡旋波束; 波束偏转

中图分类号:O436.3 文献标志码:A

Terahertz Multi-Dimensional Phase Regulated Reflection Coding Metasurface

HUANG Ruo-tong, LI Jiu-sheng^*

Center for THz Research, China Jiliang University, Hangzhou 310018, China

*Corresponding author

Abstract

Terahertz technology has a broad application prospect in communication systems. Digital codingmetasurface can control electromagnetic wave propagation and has been widely concerned. Most of the reported codingmetasurface achieve full 2πphase coverage of reflected or transmitted LP (linearly polarized) and CP (circularly polarized) waves based on PB (geometric phase) or transmission phase, limiting the flexibility of terahertz wave regulation. This paper proposes a metasurface element structure consisting of three layers, from top to bottom: the metal pattern structure layer, intermediate medium layer, and metal base layer. In this paper, a metasurface element is proposed by combining the propagation phase and geometric phase. The metasurface is designed to generate vortex beams based on the transmission phase mechanism under the incident of online polarized terahertz waves, and multi-vortex beams are generated by convolution operation. According to the geometric phase principle, phase coverage in the 2πrange can be achieved by rotating the metal pattern structure layer under the circularly polarized terahertz wave incident. The metasurface is designed to generate vortex beams based on the transmission phase mechanism under the incident of online polarized terahertz waves, and multi-vortex beams are generated by convolution operation. According to the geometric phase principle, phase coverage in the 2πrange can be achieved by rotating the metal pattern structure layer under the circular polarized terahertz wave incident. The metasurface can be properly arranged by using phase coding. The designed metasurface can deflect the reflected beam, showing good flexibility. Secondly, the designed metasurface generates vortex beams at multiple frequency points. At 0.9 THz, vortex beams with topological charges l=1 and l=2 are generated with mode purity of 68.9% and 69.5%. At 1.2 THz, vortex beams with topological charges l=1 and l=2 are generated with mode purity of 91.03% and 87.2%. In addition, the deflection vortex beam is generated by convolution, and the focusing coding metasurface is designed to realize the focusing function. In this paper, we propose a terahertz multi-dimensional phase-controlled reflection metasurface, which combines the propagation phase with the geometric phase to realize the regulation of two independent polarized channels. The results show that the designed metasurface provides a multi-degree-of-freedom method for polarization and phase manipulation of terahertz waves, which has broad application potential in terahertz systems.

Keyword: Terahertz; Phase control; Vortex beam; Terahertz deflection of beam

文章图片

引言

太赫兹技术在未来的通信中具有广阔的应用前景, 太赫兹波束的柔性操纵, 特别是波束形成和波束控制^{[1, 2]}, 已经成为研究热点。超表面是由具有亚波长尺度的二维单元阵列组成的平面人工超材料^[3], 通过对设计单元的几何参数引入不连续的传输相位调控, 可以在操纵电磁波的振幅、相位和偏振状态等方面表现出极大的灵活性^[4]。与传统的超材料相比, 超表面具有更小尺寸、更容易制造和更强大的控制电磁波的灵活性。

2014年, Cui等^[5]提出了数字编码超表面控制电磁波传输的概念, 引起了相当大的关注。数字编码超表面可以实现多种功能; 如平面偏振器^{[6, 7, 8, 9]}、平面透镜^{[10, 11]}、全息图^{[12, 13, 14]}和涡旋^{[15, 16, 17, 18]}等等。 2020年, Tian等^[19]提出了一种全介电Pancharatnam-Berry(几何相位)单元结构, 使用这些具有不同旋转角度的几何相位单元, 可以构建超表面实现波束散射角度的调控和涡旋波束生成等功能。 2022年, Li等^[20]提出了一种具有左右圆偏振和多波束的多功能编码超表面, 透射波的相位通过旋转元件来控制。 Zhang等^[21]提出了基于单层金属超表面的透射太赫兹功率分束器, 实现多分束功能。大多数报道的编码超表面基于PB相位或者传输相位实现对反射或者透射LP(线极化)和CP(圆极化)波的完全2π相位覆盖, 本文所提出的结构在两个不同的频率点独立地实现对太赫兹波的控制。线偏振波入射下, 设计的超表面实现反射波束分裂和涡旋的功能, 圆偏振波入射时, 所提出的超表面具有反射波束偏转、反射偏折涡旋生成和聚焦等功能。研究结果表明, 本文提出传输相位和几何相位相结合排布超表面, 可以实现对两个独立的极化信道进行调控, 为设计控制LP、 CP太赫兹波超表面提供了更大的自由度。

1 单元结构设计和原理分析

1.1 单元结构设计

本文提出的反射式超表面如图1所示, 其中图1(a)为超表面的功能示意图, 超表面单元结构如图1(b)和(c)所示, 单元周期为P=100 μm, 由三层介质组成, 分别为顶部金属图案, 其外径r₁=35 μm, 内径r₂=25 μm, 十字形的长m=25 μm, n=8 μm; 厚度d₁=2 μm, 中间介质层为聚酰亚胺(Polyimide), 其厚度为d₂=30 μm, 底部为金属板薄膜层(厚度h=0.5 μm)。

	Figure Option View Download New Window
	图1 反射式超表面 (a): 反射式超表面的功能示意图; (b): 超表面单元俯视图; (c): 超表面单元三维结构Fig.1 Reflective metasurface (a): Functional diagram of the reflective metasurface; (b): Top view of metasurface unit; (c): Three-dimensional structure of metasurface element

1.2 线偏振波入射下传输相位调控原理

传输相位指的是电磁波在传输的过程中会产生光程差, 利用这一光程差可实现对相位的调控。当波长为λ的电磁波在折射率为n的介质中传输距离d时, 电磁波传输相位可以表示为

$φ = (2 π / λ) nd$ (1)

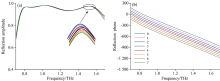
为了实现足够的相移, 超表面的结构单元需要有较大的厚度d。另外, 由于超表面结构厚度通常是均匀的, 需要改变空间每一处微结构的等效折射率n来调节传输相位, 通过改变结构的几何参数来实现。优化所设计单元结构的尺寸参数如表1所示, 利用四种不同的编码单元设计了一个2-bit编码超表面, 它具有4种编码状态00、 01、 10和11, 相位分别为-638.53°、 -533.64°、 -438.38°和-367.45°。四个单元对应的太赫兹波反射幅度和反射相位如图2所示, 从图中可见, 在0.5~1.0 THz之间, 太赫兹波反射幅度均大于0.9, 相邻编码单元的反射相位差接近90°, 满足2-bit编码超表面设计要求。

表1 2-bit编码超表面单元结构示意图和参数 Table 1 Structure diagram and parameters of 2-bit coding metasurface unit

	Figure Option View Download New Window
	图2 线偏振入射时超表面单元的反射振幅和相位 (a): 反射振幅; (b): 反射相位Fig.2 Reflection amplitude and phase of metasurface element under linear polarization incident (a): Reflection amplitude; (b): Reflection phase

1.3 圆偏振入射下PB相位调控原理

几何相位又被称为Pancharatnam-Berry (PB)相位, 通过调整具有相同尺寸结构的面内旋转角来实现全2π相位覆盖, 该相位调控机理仅适用于圆偏振入射光。根据Pancharatnam-Berry (P-B)相位原理, 入射波与反射波之间的反射传输矩阵R可表示为

$R_{θ}^{XY} = R^{- 1} (θ) [\begin{array}{l} r_{xx} & r_{xy} \\ r_{yx} & r_{yy} \end{array}] R (θ)$ (2)

式(2)中, r_xx, r_xy, r_yx和r_yy对应于线偏振波的反射系数, 第一下角标表示反射波的偏振态, 第二下标表示入射波的偏振态, r_xx表示沿x轴正方向的线偏振光入射时, 沿x轴负方向出射的反射系数。

旋转角度为θ时的旋转矩阵

$R (θ) = [\begin{array}{l} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{array}]$ (3)

对于圆偏振光入射到超表面, 反射矩阵表示为

$R_{θ}^{LR} = \frac{1}{2} [\begin{array}{l} 1 & - i \\ 1 & i \end{array}] R_{θ}^{XY} {[\begin{array}{l} 1 & - i \\ 1 & i \end{array}]}^{- 1}$ (4)

将式(2)代入到式(3)中, 可推导出圆偏振波入射下的反射矩阵为 $R_{θ}^{LR}$ = $[\begin{array}{l} r_{LL} & r_{LR} \\ r_{RL} & r_{RR} \end{array}]$ 。

$r_{LL} = \frac{1}{2} [(r_{xx} - r_{yy}) - i (r_{xy} + r_{yx}) e^{- i 2 θ}]$ (5)

$r_{RR} = \frac{1}{2} [(r_{xx} - r_{yy}) + i (r_{xy} + r_{yx}) e^{i 2 θ}]$ (6)

$r_{RL} = \frac{1}{2} [(r_{xx} + r_{yy}) + i (r_{xy} - r_{yx})]$ (7)

$r_{LR} = \frac{1}{2} [(r_{xx} + r_{yy}) - i (r_{xy} - r_{yx})]$ (8)

参数θ为单元结构相对于其中心的旋转角度, LR代表入射光的偏振态, L表示左旋偏振, R表示右旋偏振, $R_{θ}^{LR}$ 表示圆偏振光入射时的反射矩阵。

左旋极化波电场可以表示为E_in= $[\begin{array}{l} 1 \\ i \end{array}]$ , 当太赫兹波入射到超表面后, 反射电场可以描述为

$\begin{array}{l} E_{out}^{r} = R_{θ}^{LR} E_{in} = \frac{1}{2} [(r_{xx} + r_{yy} + r_{xy} + r_{yx}) (\begin{array}{l} 1 \\ i \end{array})] + \\ \frac{1}{2} [(r_{xx} - r_{yy} + r_{xy} - r_{yx}) e^{i 2 θ} (\begin{array}{l} i \\ 1 \end{array})] \end{array}$ (9)

出射波的右旋极化分量携带了2θ相位因子, 而左旋圆极化没有改变。因此, 超表面可以将入射的圆极化波转换为交叉极化波, 并且通过旋转单元结构实现出射相位2π范围覆盖。

表2 圆偏振下的超表面单元 Table 2 The unit cell under circular polarization

	Figure Option View Download New Window
	图3 圆偏振入射下, 超表面单元反射振幅和反射相位 (a): 反射振幅; (b): 反射相位Fig.3 Reflection amplitude and phase of metasurface element under circular polarization incident (a): Reflection amplitude; (b): Reflection phase

2 线偏振入射

2.1 涡旋波束

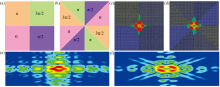
涡旋波通常是由螺旋相板或圆形光栅产生, 为了产生整数拓扑电荷l=1和l=2的涡旋, 需要产生一个以相位因子exp(ilφ )为特征的螺旋波前。将超表面划分为n个相等的角度的2π/n个区域, 相邻区域的反射相位差固定为Δφ , 其中n, l和Δφ 之间的关系为nΔφ =2πl。图4(a)和(c)给出了产生两种涡旋波的超表面原理图, 利用CST仿真得到了两种涡旋波的三维远场图和二维电场图, 如图4(b), (d), (e)和(f)所示, 设计的两种超表面实现了涡旋波束的产生。

Figure Option
View Download New Window

图4 线偏振下涡旋波产生原理图和远场图
(a): l=1涡旋波相位分布图; (b): l=1涡旋波的三维远场图; (c): l=2涡旋波相位分布图; (d): l=2涡旋波的三维远场图; (e): l=1涡旋波的二维电场图; (f): l=2涡旋波的二维电场图Fig.4 Schematic diagram and far-field diagram of vortex wave generation under linear polarization
(a): Phase distribution of vortex wave with l=1; (b): Three-dimensional far-field diagram of vortex wave with l=1; (c): Phase distribution of vortex wave with l=2; (d): Three-dimensional far-field diagram of vortex wave with l=2; (e): Two-dimensional electric field diagram of vortex wave with l=1; (f): Two-dimensional electric field diagram of vortex wave with l=2

2.2 多涡旋波束

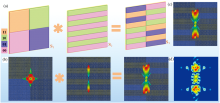
设计的卷积超表面通过卷积涡旋波束和多分束的梯度编码序列生成了多涡旋波束。生成双涡旋波束的卷积过程如图5(a, b)所示, 在0.66 THz处, 利用CST模拟仿真了太赫兹线偏振波法向入射下超表面S₃产生的三维远场和二维电场, 如图5(c, d)所示。从图中可以看出超表面S₃产生了两个具有一定偏转角度的涡旋波束, 其偏转角度与两分束编码序列的反射波束相同。其次, 通过超表面S₁和超表面S₄卷积运算生成的一个超表面S₅, 如图6(a, b)所示, 在0.66 THz线偏振波入射下, 超表面S₅产生了四个反射涡旋波束, 三维远场和二维电场如图6(c, d)所示。

Figure Option
View Download New Window

图5 产生双涡旋波束
(a): 涡旋叠加两分束生成双涡旋波束卷积运算的超表面单元排布; (b): 涡旋叠加四分束生成四涡旋波束的三维远场图; (c): 双涡旋波束的三维远场图; (d): 双涡旋波束的二维电场图Fig.5 Generation of double vortex beam
(a): The superposition of vortices with two beams generates the metasurface element arrangement of the double-vortex beam convolution operation; (b): The superposition of vortices with four beams generates the three-dimensional far-field diagram of the four-vortex beam; (c): The three-dimensional far-field diagram of the double-vortex beam; (d): The two-dimensional electric field diagram of the double-vortex beam

Figure Option
View Download New Window

图6 产生四涡旋波束
(a): 涡旋叠加四分束生成四涡旋波束卷积运算的超表面单元排布; (b): 涡旋叠加四分束生成四涡旋波束的三维远场图; (c): 四涡旋波束的三维远场图; (d): 四涡旋波束的二维电场图Fig.6 Generation of four-vortex beam
(a): Vortex superimposed quadricle generates metassurface-element arrangement of quadricle beam convolution operation; (b): Vortex superimposed quadricle generates three-dimensional far-field diagram of quadricle beam; (c): Three-dimensional far-field diagram of quadricle beam; (d): Two-dimensional electric field diagram of quadricle beam

3 圆偏振入射

3.1 涡旋波束

当平面波垂直入射到超表面阵列时, 要转化成拓扑荷数为l的涡旋波束, 超表面上的相位分布φ 可以表示为

$φ_{m} (x, y) = l \cdot ta n^{- 1} (\frac{y}{x})$ (10)

式(10)中, (x, y)为超表面单元在二维坐标系中的具体位置, 提出的超表面可以划分为N个三角形区域, 每个区域的相位分布可通过式(11)计算

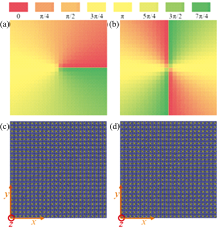
$φ_{m} (x, y) = \frac{2 π}{N} [\frac{l \cdot ta n^{- 1} (y / x)}{2 π / N} + 1]$ (11)

式(11)中, N是超表面被划分的区域数。所提出的超表面生成拓扑荷数l=1和l=2的涡旋波束, 波前相位的覆盖范围是0~2π、 0~4π。图7给出了生成不同拓扑荷数(l=1、 l=2)涡旋波束的超表面相位分布及其相对应排布而成的超表面结构。图7(a)和(b)表示拓扑荷数l=1和l=2时涡旋超表面相位分布, 对应单元结构阵列排布获得超表面如图7(c)和(d)所示。

Figure Option
View Download New Window

图7 圆偏振波入射下, 产生涡旋波束的相位分布和单元阵列排布
(a): 圆偏振下l=1涡旋波束产生的相位分布图; (b): 圆偏振下l=2涡旋产生的相位分布; (c): l=1涡旋单元阵列排布; (d): l=2涡旋单元阵列排布Fig.7 Phase distribution and element array arrangement of vortex beam generated by circularly polarized wave in cident
(a): Phase distribution of vortex beam with l=1 in circular polarization; (b): Phase distribution of vortices with l=2 in circular polarization; (c): l=1 vortex element array arrangement; (d): l=2 vortex element array arrangement

为了定量说明产生涡旋波束的质量, 需要对其产生涡旋波的模态以及纯度进行分析。根据傅里叶变换原理, 方位角φ 是一个周期性的函数, 对应傅里叶共轭是一个离散变量, 通常OAM模式纯度越大, 其相对应的涡旋波束质量越高。相应的傅里叶共轭是涡旋波束谱, 这种关系可以表示为式(12)

$\{\begin{array}{l} Ψ (φ) = \overset{+ \infty}{\sum_{l = - \infty}} A_{l} \cdot \exp (ilφ) \\ A_{l} = \frac{1}{2 π} \int_{-}^{π} d φα (φ) \cdot \exp (ilφ) \end{array}$ (12)

式(12)中, Ψ (φ )是相位的采样, exp(ilφ )是螺旋谐波, A_l表示拓扑荷数为l的光谱模式权重, 产生涡旋波束的模式纯度定义为主模功率与分布在所有模态上的总功率之比。

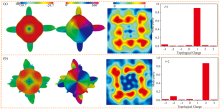
当RCP波束垂直入射到超表面时, 在0.9 THz处可以产生拓扑荷数l=1和l=2的涡旋波束。从图8(a)可以看出, 超表面产生的反射拓扑荷数为l=1太赫兹涡旋波束的远场强度、远场相位、电场振幅和模式纯度。图中的中空环形振幅和2π螺旋相位分布可以看出该超表面结构产生的涡旋波束拓扑荷数为1, 其涡旋波束的模式纯度为68.9%。同样地, 图8(b)表示所设计超表面产生的反射拓扑荷数为l=2涡旋波束的远场强度、远场相位、电场振幅和模式纯度。可见产生l=2涡旋波束与预设排布相符合, 涡旋波束的模式纯度为69.5%。在频率1.2 THz处该超表面也产生了涡旋波束, 超表面产生的l=1和l=2太赫兹反射涡旋波束的远场强度、远场相位、电场振幅和模式纯度如图9(a, b)所示。相比于在0.9 THz处产生的涡旋波束, 在1.2 THz处的涡旋波束模式纯度更高, 拓扑荷数l=1和l=2分别为91.03%和89.2%。

	Figure Option View Download New Window
	图8 频率0.9 THz处涡旋波束在不同拓扑荷数下的远场强度、远场相位、电场强度图和模式纯度 (a): l=1; (b): l=2Fig.8 Far-field intensity, far-field phase, electric field intensity and mode purity of 0.9 THz vortex beam under different topological charges (a): l=1; (b): l=2

	Figure Option View Download New Window
	图9 频率1.2 THz处涡旋波束在不同拓扑荷数下的远场强度、远场相位、电场强度图和模式纯度 (a): l=1; (b): l=2Fig.9 Far-field intensity, far-field phase, electric field intensity and mode purity of 1.2 THz vortex beam under different topological charges (a): l=1; (b): l=2

3.2 太赫兹波异常反射

超表面利用相位突变的梯度进行调控波束异常反射, 我们可以计算出反射角

$θ = \arcsin (λ / Γ)$ (13)

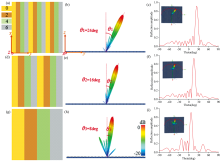
式(13)中, λ是入射波长, Γ 是相位梯度的周期。太赫兹波的反射角可以通过改变特定入射波长和相位梯度周期来调节。排布M₁(Γ ₁=4×2×100 μm=800 μm)、 M₂(Γ ₂=4×3×100 μm=1 200 μm)和M₃(Γ ₃=4×6×100 μm=2 400 μm)如图10(a)、 (d)和(g)所示, 在0.9 THz处圆偏振波入射下, 该超表面的三维远场散射模式如图10(b)、 (e)和(h)所示, 可见, 反射波束与+z轴之间存在一个偏转角θ, 偏转角度为θ₁=24°, θ₂=16°和θ₃=8°。式(13)计算θ₁=24.62°, θ₂=16.12°, θ₃=7.98°, 仿真计算结果与理论预测一致。得到归一化反射光谱如图10(c)、 (f)、 (i)所示, 随着入射波长(编码周期)的变化, 反射幅度最高值所对应的角度在改变, 进一步验证了该太赫兹超表面可以通过改变预先设计的编码序列来产生具有可控制方向的异常反射。

Figure Option
View Download New Window

图10 异常反射偏折波束的生成
(a), (d), (g): 超表面M₁、 M₂、 M₃的单元排布; (b), (e), (h) : M₁、 M₂、 M₃的三维远场图案; (c), (f), (i): M₁、 M₂、 M₃的归一化反射强度能量振幅图Fig.10 Generation of abnormal reflection deflected beam
(a), (d), (g): The element arrangement of coding metasurface M₁, M₂ and M₃; (b), (e), (h): The three-dimensional far-field pattern of M₁, M₂ and M₃; (c), (f), (i): The normalized reflection intensity energy amplitude diagram of M₁, M₂ and M₃

编码超表面可以通过叠加和卷积运算, 可将入射的太赫兹波束反射到任意角度。

$θ = \arcsin (\sqrt[]{si n^{2} θ_{1} \pm si n^{2} θ_{2}})$ (14)

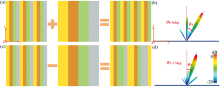
式(14)中, θ₁和θ₂分别对应于卷积运算的两个梯度编码序列的散射角, 这两个序列模式被相加或相减, 卷积过程如图11(a, b)所示。图11(a)可见, M₄是沿y方向的梯度编码序列M₁和沿y方向的梯度编码序列M₃的卷积运算相加得到, 卷积得到的编码序列的三维远场图如图11(c)所示, 单个反射波束的偏转角θ₄=34°, 这与理论预测的33.74°基本一致。类似地, 从图11(b)中可以看出, M₅是沿y方向的梯度编码序列M₁和沿y方向的梯度编码顺序M₃的卷积运算相减得到, 单束散射角约为θ₅=17°, 如图11(d)中三维远场图案所示, 与理论值θ₅=16.64°吻合较好, 进行卷积运算可以更灵活地调整单个波束的偏转角度。

	Figure Option View Download New Window
	图11 异常反射偏折波束的卷积运算 (a): M₁+M₃=M₄; (b): M₁-M₃=M₅; (c), (d): M₄、 M₅的三维远场图Fig.11 Convolution operation of abnormally reflected deflected beam (a): M₁+M₃=M₄; (b): M₁-M₃=M₅; (c), (d): Three-dimensional far-field diagram of M₄ and M₅

3.3 偏折涡旋

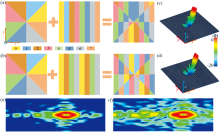
图12(a, b)显示了设计的偏折涡旋波束的卷积运算过程, 使正入射的太赫兹波反射生成具有一定偏转角度的涡旋波束。卷积运算来自于沿x方向的涡旋波束生成编码序列和梯度编码序列“01234567和02460246”的加法, 对卷积运算的编码超表面在CST中进行了模拟仿真, 验证了理论预测结果, 卷积运算编码超表面的涡旋波束散射角为14°和10°, 图12(c—f)表示偏折涡旋波束的三维远场图和二维电场强度图, 仿真得到的三维远场图可以看出涡旋波束距离z轴有一定的偏转角度, 涡旋波束距离中心点有一定的偏移, 可见通过将两个编码序列相加卷积运算可以获得不同的偏转角度的涡旋波束。

Figure Option
View Download New Window

图12 偏折涡旋波束的生成和三维远场图、二维电场图
(a), (b): 涡旋波束偏折的卷积运算; (c), (d): 偏折涡旋波束的三维远场图; (e), (f): 偏折涡旋波束的二维电场图Fig.12 Generation of deflected vortex beam, three-dimensional far-field diagram and two-dimensional electric field diagram
(a), (b): Convolution operation of vortex beam deflection; (c), (d): Three-dimensional far-field diagram of deflected vortex beam; (e), (f): Two-dimensional electric field diagram of deflected vortex beam

3.4 聚焦

为了实现平面结构的聚焦, 该结构需要等相位波前。每个粒子的反射相位应补偿空间相位延迟。对于具有给定焦距f的超表面每个单元的相移φ 满足式(14)

$φ = 2 π (\sqrt[]{x^{2} + y^{2} + f^{2}} - f) / λ$ (14)

式(14)中, f是焦距, (x, y)是每个单元的中心坐标。

为了确定编码单元的中心坐标, 将整个超表面中心定义为绝对坐标(0, 0), 单元的宽度设置为100 μm, 每个单元的水平和垂直坐标可通过相位计算确定。设计焦距f=1 500 μm的聚焦超表面, 相位排布如图13(a)所示, 利用CST进行模拟仿真, 得到的结果如图13(b)和(c)所示。在0.8 THz处太赫兹波入射到超表面时, z=1 500 μm时的x-y截面如图13(b)所示, 可以观察到预设的焦点在中心处显示出来。图13(c)说明了x=0 μm处y-z截面的聚焦, 在z=1 500 μm处具有明显的聚焦效果, 模拟结果与理论预测一致。

	Figure Option View Download New Window
	图13 反射聚焦 (a): 反射聚焦相位排布; (b): z=1 500 μm处x-y截面的二维电场图; (c): x=0处y-z截面的二维电场图Fig.13 Reflection focusing (a): Reflection focusing phase arrangement; (b): Two-dimensional electric field diagram of x-y section at z=1 500 μm; (c): Two-dimensional electric field diagram of y-z section at x=0

4 结论

提出了一种基于多维度相位调控的太赫兹反射超表面, 在0.5~1.7 THz内, 传输相位和几何相位可以独立地操纵反射线偏振和圆偏振波前, 实现了偏振复用。超表面可以在不同极化的平面波入射下实现多分束、异常反射和多反射涡旋波束等多种功能, 当线偏振波入射时, 设计的超表面具有反射波束分裂和涡旋波束的功能, 当圆偏振波入射时, 所提出的超表面可以实现反射波束偏转、反射偏折涡旋波束生成和聚焦的功能。多种功能是通过单元中不同功能序列予以实现, 通过改变入射波极化、入射方向以及频率等自由度来减少不同功能之间的相互干扰。分析研究结果可以发现, 设计的超表面提供了一种多自由度的太赫兹波偏振和相位操控方法, 在太赫兹系统具有广阔的应用潜力。

参考文献

文献列表

[1]	Yang J, Yin M, Gao H, et al. Chinese Journal of Electronics, 2022, 31(3): 581. [本文引用:1]
[2]	Erçağlar V, Hajian H, Serebryannikov A E, et al. Optics Letters, 2021, 46(16): 3953. [本文引用:1]
[3]	Fu X, Shi L, Yang J, et al. ACS Applied Materials & Interfaces, 2022, 14(18): 22287. [本文引用:1]
[4]	Li W, Zhao G, Meng T, et al. Chinese Physics B, 2021, 30(5): 058103. [本文引用:1]
[5]	Cui T J, Qi M Q, Wan X, et al. Light: Science & Applications, 2014, 3(10): e218. [本文引用:1]
[6]	Sorathiya V, Lavadiya S, AlGhamdi A, et al. Journal of Computational Electronics, 2022, 21(1): 280. [本文引用:1]
[7]	Yue Z, Li J, Li J, et al. Opto-Electronic Science, 2022, 1(3): 210014-1. [本文引用:1]
[8]	Lerer A M, Makeeva G S, Golovanov O A. Radiophysics and Quantum Electronics, 2020, 62(10): 700. [本文引用:1]
[9]	Yang Z, Yu D, Zhang H, et al. Nanomaterials, 2021, 11(7): 1851. [本文引用:1]
[10]	Azad A K, Efimov A V, Ghosh S, et al. Applied Physics Letters, 2017, 110(22): 224101. [本文引用:1]
[11]	He X, Yang Y, Deng L, et al. ACS Applied Materials & Interfaces, 2021, 13(17): 20770. [本文引用:1]
[12]	He J, Dong T, Chi B, et al. Microelectronic Engineering, 2020, 220: 111151. [本文引用:1]
[13]	Hu M, Tian Z, Chen X, et al. IEEE Photonics Journal, 2020, 12(4): 5900309. [本文引用:1]
[14]	Liao D, Chan K F, Chan C H, et al. Optics Letters, 2020, 45(10): 2906. [本文引用:1]
[15]	Cheng K, Hu Z, Wang Y, et al. Optics Letters, 2020, 45(21): 6054. [本文引用:1]
[16]	Yang Q, Wang Y, Liang L, et al. Optical Materials, 2021, 121: 111574. [本文引用:1]
[17]	Zhang L, Li J S. Optical and Quantum Electronics, 2022, 54(4): 209. [本文引用:1]
[18]	Li W, Zhao G, Meng T, et al. Chinese Physics B, 2021, 30(5): 058103. [本文引用:1]
[19]	Tian Y, Jing X, Yu H, et al. Optics Express, 2020, 28(21): 32107. [本文引用:1]
[20]	Li S, Li Z, Han B, et al. Front. Mater. , 2022, 9: 854062. [本文引用:1]
[21]	Zhang C, Li C, Fang B, et al. Applied Optics, 2022, 61(14): 4153. [本文引用:1]

2022

0.0

... 引言太赫兹技术在未来的通信中具有广阔的应用前景, 太赫兹波束的柔性操纵, 特别是波束形成和波束控制^[1,2], 已经成为研究热点 ...

2021

0.0

... 引言太赫兹技术在未来的通信中具有广阔的应用前景, 太赫兹波束的柔性操纵, 特别是波束形成和波束控制^[1,2], 已经成为研究热点 ...

2022

0.0

... 超表面是由具有亚波长尺度的二维单元阵列组成的平面人工超材料^[3], 通过对设计单元的几何参数引入不连续的传输相位调控, 可以在操纵电磁波的振幅、相位和偏振状态等方面表现出极大的灵活性^[4] ...

2021

0.0

2014

0.0

... 2014年, Cui等^[5]提出了数字编码超表面控制电磁波传输的概念, 引起了相当大的关注 ...

2022

0.0