引用本文
吕树彬, 杨婉琪, 李福生. 基于主成分分析和宽度学习系统的土壤铅镉重金属元素定量分析[J]. 光谱学与光谱分析, 2024,44(7): 1852-1857.
LÜ Shu-bin, YANG Wan-qi, LI Fu-sheng. Quantitative Analysis of Lead and Cadmium Heavy Metal Elements in Soil Based on Principal Component Analysis and Broad Learning System[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1852-1857.
Doi:10.3964/j.issn.1000-0593(2024)07-1852-06  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于主成分分析和宽度学习系统的土壤铅镉重金属元素定量分析
吕树彬1,2, 杨婉琪1,2, 李福生1,2,*
1.电子科技大学自动化工程学院, 四川 成都 611731
2.电子科技大学长三角研究院(湖州), 浙江 湖州 313001
*通讯作者 e-mail: lifusheng@uestc.edu.cn

作者简介: 吕树彬, 1996年生,电子科技大学自动化工程学院及长三角研究院博士研究生 e-mail: sicrilemy@163.com

收稿日期: 2022-12-10 修回日期: 2023-09-25
基金: 国家自然科学基金项目(62075028)资助
摘要

在土壤重金属元素定量分析研究中, X射线荧光分析(XRF)是一种有效的无损分析技术。 由于受到矩阵效应以及元素干扰的影响, 已有的机器学习方法在利用土壤XRF光谱预测铅(Pb)元素、 镉(Cd)元素浓度时存在性能不足和不稳定的问题。 该工作提出了基于主成分分析(PCA)结合宽度学习系统(BLS)的XRF土壤重金属元素定量分析方法(PCA-BLS), 用于精确、 高效、 稳定测定土壤中Pb元素和Cd元素的浓度。 使用PCA对56个标准土壤数据进行特征降维, 并选取Pb和Cd的前3个主成分作为特征。 将最优主成分特征输入宽度学习系统进行校正和测试, 并使用网格搜索算法确定最佳网络结构。 其中Pb元素和Cd元素对应的BLS的三个最优参数值分别为2, 11, 11和3, 19, 15。 使用支持向量回归(SVR)、 BP神经网络和原始BLS三种模型与PCA-BLS方法进行对比。 PCA-BLS在测定Pb对应的决定系数 R2、 均方根误差RMSE和平均绝对百分比误差MAPE三个指标上取得了0.954、 1.433、 1.014的结果, 在定量Cd实验中取得 R2为0.982、 RMSE为1.215和MAPE为1.059的精度。 网格搜索可视化表明PCA-BLS在预测两种重金属元素时具有稳定的性能。 实验结果表明, PCA-BLS可以有效校正土壤XRF光谱中的矩阵效应和干扰, 在准确预测Pb和Cd元素浓度的同时保持模型稳定性, 是一种具有潜力的XRF光谱定量分析方法。

关键词: 土壤重金属; XRF定量分析; 宽度学习系统; 主成分分析
中图分类号:O434.13 文献标志码:A
Quantitative Analysis of Lead and Cadmium Heavy Metal Elements in Soil Based on Principal Component Analysis and Broad Learning System
LÜ Shu-bin1,2, YANG Wan-qi1,2, LI Fu-sheng1,2,*
1. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China
2. Yangtze River Delta Research Institute, University of Electronic Science and Technology of China (Huzhou), Huzhou 313001, China
*Corresponding author
Abstract

X-ray fluorescence analysis (XRF) is a remarkably effective analytical technique for quantitatively studying heavy metal elements in soils. Due to matrix effects and elemental interferences, existing machine-learning methods suffer from inadequate performance and instability in predicting lead (Pb) and cadmium (Cd) concentrations using soil XRF spectra. Therefore, this paper proposes a PCA-BLS method for the XRF quantitative analysis of heavy metals in soil based on principal component analysis (PCA) combined with the broad learning system (BLS). It can accurately, efficiently, and stably determine concentrations of Pb and Cd in soil. First, the 56 standard soil data are feature-reduced using PCA. The first three principal components of Pb and Cd are selected as features. Then, the optimal principal component features are fed into the width learning system for calibration and testing. Using the grid search determine the optimal network structure. The three optimum parameters for the BLS corresponding to the Pb and Cd elements are 2, 11, 11 and 3, 19, 15, respectively. Using support vector regression (SVR), BP neural network, and the original BLS compared with the PCA-BLS. PCA-BLS achieved performances of 0.954, 1.433, and 1.014 in the R2, RMSE, and MAPE corresponding to Pb. In the quantitative Cd, PCA-BLS obtains the R2 of 0.982, RMSE of 1.215, and MAPE of 1.059. Grid search visualization demonstrates the stable performance of PCA-BLS in predicting two heavy metal elements. The experimental results show that PCA-BLS can effectively correct for matrix effects and interferences in soil XRF. The PCA-BLS is a promising method for quantitative XRF spectroscopy that accurately predicts Pb and Cd elemental concentrations while maintaining model stability.

Keyword: Soil heavy metals; XRF quantitative analysis; Broad learning system; Principal component analysis
引言

随着经济水平的提高, 频繁的工业、 农业活动使得土壤受到了不同程度的污染, 这不仅破坏了人类生存的环境, 同时还威胁到人类自身的健康, 土壤污染是一个亟待解决的现实问题[1]。 如何评估土壤污染程度, 特别是对土壤中重金属元素的测量和估计是一个复杂的问题。 土壤中的重金属存在滞后性和积累性, 因此很难及时发现[2]; 工业、 农业等人类活动使得土壤污染评估更加困难[3]。 传统的化学分析技术存在较多限制, 很难满足实际应用需求。 因此, 高效、 精确、 稳定测定土壤中重金属元素含量, 对土壤状态的评估和土壤的治理具有非常重要的意义[4]。

X射线荧光分析(XRF)作为一种无损元素检测技术, 现已广泛应用于环境、 农产品等无机元素的测定。 由于其多元素测定、 制样方法简单和便携等特性, 在土壤重金属元素含量测定中具有显著的优势。 在利用该技术定量分析重金属元素浓度时, 容易受到基体效应的影响, 使得重金属元素的测定, 尤其是铅(Pb)、 镉(Cd)等元素的测定结果受到严重干扰。 由于基体效应是一种非线性关系, 传统的实验校正和数学校正方法均难以取得令人满意的结果[5]。 随着神经网络、 启发式优化算法等新型人工智能方法的不断涌现, 精确元素定量分析已经成为可能[6]。 江晓宇等将竞争性自适应重加权算法(CARS)和偏最小二乘方法(PLS)用于江西鄱阳湖地区土壤中铅砷两种重金属元素的浓度测定[7]。 受到土壤样本数量以及方法拟合能力的影响, 现有的定量分析方法无法充分拟合不同元素强度和浓度之间的非线性关系, 浓度测定精度有限。

主成分分析(PCA)是一种将原始数据转换到新的坐标参考系统的统计方法[8], 它可以减少冗余特征, 缓解高维数据中存在的多重共线性问题, 降低定量分析难度。 Yang等将PCA、 方差分析(ANOVA)和支持向量回归(SVR)方法结合, 实现了土壤中V、 Cr、 Cu等重金属元素的精确定量[12]。 宽度学习系统(BLS)是一种新颖的神经网络结构, 可以同时利用线性逼近和非线性逼近的优势提升方法的拟合能力[9, 10]。 依靠简单的扁平式结构建模, 宽度学习系统可以在显著提升计算效率的同时, 获得令人满意的精度[11]。 乔继红等将宽度学习系统用于近红外光谱的国外奶粉产地识别研究, 实现了国外奶粉产地的准确鉴别[13]。

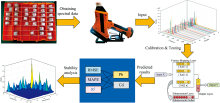
本文提出一种使用PCA和BLS结合的XRF土壤重金属元素定量分析方法, 用于标准土壤样品中Pb和Cd元素的浓度测定。 使用PCA方法对原始光谱数据进行降维, 以减少光谱样本中的噪声信息。 将降维后的光谱数据输入宽度学习系统进行校正和测试, 并使用网格搜索确定最优网络结构。 使用决定系数(R2)、 均方根误差(RMSE)和平均绝对百分比误差(MAPE)评估方法性能, 并与支持向量回归(SVR)、 反向传播神经网络(BPNN)进行比较。 本工作的完整流程如图1所示。

图1 土壤Pb、 Cd元素定量分析流程图Fig.1 Flow chart for quantitative analysis of soil Pb and Cd elements

1 实验部分
1.1 土壤样本

所使用的56个土壤样本均采购于中国标准物质网, 其中包括26个土壤标准物质(GSS系列)、 26个水系沉积物标准物质(GSD系列)、 4个系列土壤成分分析标准物质(GBW(E)系列)。 不同样本均按照采集、 风干、 研磨、 过筛的步骤进行处理[12], 并使用TS-XH4000型号的ED-XRF光谱仪进行XRF荧光光谱的测定。 所获取的在0~45 keV能量范围内的光谱数据共包含2 048个通道数。 为了便于观察, 只选取前600个通道的谱图, 所有土壤样品主要光谱信息如图2(a)所示。 以GBW07384(GSD-33)土壤样本为例, 该样本的谱图如图2(b)所示。 其中用于定量分析的元素Pb和Cd的统计信息如表1所示。

图2 土壤XRF光谱可视化
(a): 56个土壤样品对应的XRF光谱图; (b): GBW07384(GSD-33)样本的元素信息Fig.2 Soil XRF spectroscopy visualization
(a): XRF spectra corresponding to 56 soil samples; (b): Elemental information for sample GBW07384 (GSD-33)

表1 土壤样品中Pb和Cd的统计信息 Table 1 Statistical information of elemental Pb and elemental Cd in soil samples
1.2 主成分分析(PCA)

在对高维光谱数据进行定量分析时, 变量个数太多会增加定量分析模型的复杂性, 影响定量分析的效果[8]。 主成分分析作为一种广泛使用的多元统计方法, 利用坐标变换将存在相关性的原始变量转换为主成分, 可以显著减少变量的个数, 同时保证降维后的特征尽可能反映原有变量的内部结构信息。 使用时将数据划分为校正集和测试集, 并根据校正集的方差累计贡献率确定主成分个数。 在测试阶段, 将测试集数据与训练集的投影矩阵相乘并获得测试集特征。 其中方差贡献率越大说明该主成分包含的有效信息越多。 因此, PCA在提取XRF光谱中的有效信息时具有优势。

1.3 宽度学习系统(BLS)

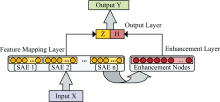
宽度学习系统主要由三个基本部分组成, 特征映射层、 增强层和输出层。 特征映射层提取数据中的有效特征, 同时使用多个稀疏自编码器构建特征映射层的稀疏特征以达到进一步降维的目的。 稀疏自编码器(SAE)是一种无监督降维方法, 可以利用编码输出与原输入的误差提取输入数据中的有效信息[9]。 增强层主要对特征映射层的输出执行非线性变换, 使得方法具有更强的非线性逼近能力。 输出层用于复用特征映射层的输出以及增强层的输出, 使得宽度学习系统可以通过伪逆算法更新两层的权重。 宽度学习系统同时具备线性映射和非线性映射能力, 可以有效对复杂数据, 尤其是高维数据进行建模。 宽度学习系统具有浅层和快速重构的特性, 因此相比其他机器学习和深度学习方法具有更加显著的计算效率优势。 宽度学习系统的流程图如图3所示。

图3 宽度学习系统流程图Fig.3 Flow chart of the broad learning system

2 结果与讨论
2.1 光谱预处理

为了归纳和统一样本的统计分布特性, 提升机器学习模型的拟合效率, 首先使用标准化方法对光谱数据进行预处理, 确保特征可以缩放到合理的范围。 将所获得的56个标准土壤样品按照8∶2的比例随机划为校正集和测试集。

2.2 主成分分析(PCA)降维结果

将经过预处理的样本进行主成分分析, 以进一步提取土壤样本的有效信息。 每个土壤样品总共包含2 048个通道的光谱变量, 使用主成分分析提取特征。 图4为校正集土壤XRF光谱在经过PCA主成分分析方法后, 不同主成分方差贡献率排序的碎石图。 其中Pb元素对应的3个主成分方差贡献率分别为52.301 9%, 33.167 2%和8.594 7%, 其余主成分之和为5.936 2%。 Cd元素对应的3个主成分方差贡献率为50.061 8%, 34.473%, 10.071 7%, 其余主成分之和为5.393 5%。 土壤光谱数据的有效信息主要集中在前3个主成分, 而后续成分所包含的有效信息相对较少。 为了减少光谱中的无关信息, 选择方差累计贡献较大的前三个主成分作为Pb和Cd元素定量分析的特征, 用于后续浓度测定。

图4 Pb元素和Cd元素的主成分碎石图
(a): Pb; (b): CdFig.4 Principal component scree plot of Pb and Cd
(a): Pb; (b): Cd

2.3 宽度学习系统定量分析

2.3.1 指标和参数选择

将PCA处理后的Pb和Cd元素数据输入宽度学习系统, 执行浓度校正和测试。 用于性能对比的机器学习方法包括SVR[14]、 BP神经网络[15]和原始BLS。 所使用的评估指标包括决定系数(R2), 均方根误差(RMSE)以及平均绝对百分比误差(MAPE), 具体指标计算公式如式(1)—式(3)所示

R2=1-∑i=1N(Yi-Ŷ)2∑i=1N(Yi-Y¯)2(1)

RMSE=1N∑i=1N(Yi-Ŷi)2(2)

MAPE=100%/N∑i=1N|(Ŷi-Yi)/Yi|(3)

式(1)—式(3)中,Ŷ为土壤元素预测浓度, Yi土壤元素真实浓度。 N为样本数量。 校正集中的特征节点数量NumFeature、 特征节点组数量NumGroup和增强节点数量NumEnhan三个超参数使用网格搜索进行寻优, 并指定搜索范围分别为[1, 20], [1, 20]和[1, 200]。 经过网格搜索, 最终确定Pb元素和Cd元素对应的三个最优超参数值分别为2, 11, 11和3, 19, 15。 为了进一步展示PCA-BLS的稳定性, 将增强节点数量固定为15, 并在特征节点数量和特征节点组数量范围为[1, 20]内进行网格搜索, 评价指标选择RMSE。 最终Pb和Cd元素对应的超参数网格搜索RMSE结果如图5(a, b)所示。 从图5可以看出, PCA-BLS性能对于超参数的变化较为稳定, 不会出现极端性能变差的情况。 当特征节点数量和特征节点组数量小于5时, 模型性能会出现一定程度的波动。 随着特征节点数和特征节点组数的上升, PCA-BLS可以使Pb和Cd的RMSE维持在较低的RMSE。 由此可见, PCA-BLS在预测Pb元素和Cd元素浓度时, 其性能可以保持良好的稳定性。

图5 网格搜索可视化
(a): Pb元素的网格搜索结果; (b): Cd元素的网格搜索结果Fig.5 Grid search visualization
(a): Grid search results for the Pb; (b): Grid search results for the Cd

2.3.2 Pb和Cd元素定量分析

采用SVR、 BPNN、 BLS和PCA-BLS建立了两种不同元素的预测模型, 模型的最优结构均使用网格搜索, 各模型的Pb、 Cd元素浓度预测结果如图6(a, b)所示。 为了进一步比较这些方法在定量分析中的有效性, 表2为不同方法在Pb元素和Cd元素定量测定中的性能表现。 结果表明, PCA-BLS在Pb元素定量测定实验中取得了最优校正精度和最优测试精度。 其中在测试集中, R2为0.954, RMSE为1.433, MAPE为1.014。 相比于BLS方法, PCA-BLS具有更加优越的性能, 说明PCA和SAE提取了光谱数据中的有效信息。 而与其他机器学习方法相比, PCA-BLS取得了显著优于其他方法的性能。 PCA-BLS在测试集上的R2分别比SVR和BPNN高0.247和0.239, 在测试集上的RMSE分别比SVR和BPNN低2.897和2.648, 在测试集上的MAPE分别比SVR和BPNN低1.427和1.323。 可以看出, BLS在Pb定量测定中具有更好的逼近能力和变量解释能力。 在Cd元素的定量分析实验中, PCA-BLS在校正集的R2指标上取得了0.966的精度, 在测试集的R2上取得了0.982的精度优势。 由于Cd元素在土壤样品中浓度较低, 并且不同样品的Cd元素浓度差异较大, 因此在使用机器学习方法进行校正对会容易过拟合。 而BLS对测试集的拟合能力和变量解释能力显著优于其他机器学习方法, 因此并没有出现严重的过拟合现象。 BLS在校正集上可以获得最优精度, 而PCA-BLS在测试集上的性能更好。 在对更加复杂的重金属元素光谱数据建模中, BLS有潜力获得更好的拟合能力和泛化能力。

图6 SVR、 BPNN、 BLS和PCA-BLS的预测结果
(a): Pb元素预测结果; (b): Cd元素预测结果Fig.6 Predicted results for SVR, BPNN, BLS, and PCA-BLS
(a): Predicted results for Pb; (b): Predicted results for Cd

表2 Pb和Cd元素定量测定结果 Table 2 Quantitative determination results of Pb and Cd elements
3 结论

尝试构建了新的用于定量分析XRF土壤重金属元素的机器学习方法, 基于主成分分析的宽度学习系统。 首先, 使用PCA主成分分析对56个标准土壤XRF光谱数据降维, 根据方差累计贡献率确定了前3个最佳主成分。 然后, 将PCA提取的特征输入BLS, 网格搜索算法确定了Pb和Cd对应的最佳BLS结构参数为2, 11, 11和3, 19, 15。 使用经过网格搜索优化的SVR、 BPNN和BLS与PCA-BLS方法进行性能比较。 其中PCA-BLS在测试阶段Pb和Cd的R2指标取得了0.954和0.982的最优拟合精度。 实验结果表明, PCA方法有效缩减了土壤样品的变量数量, 简化了BLS的复杂性。 相比于其他机器学习方法, PCA-BLS在浓度测定实验中具有更好的校正能力、 泛化能力和稳定性。 上述方法满足了基于XRF的土壤重金属元素精确、 高效、 稳定定量分析的需求, 为重金属元素定量分析方法的拓展提供了新的方向。

参考文献
[1] Li F, Yang W, Ma Q, et al. Measurement Science and Technology, 2021, 32(10): 105501. [本文引用:1]
[2] Bai B, Xu T, Nie Q, et al. International Journal of Heat and Mass Transfer, 2020, 153: 119573. [本文引用:1]
[3] Sergeev A P, Buevich A G, Baglaeva E M, et al. Catena, 2019, 174: 425. [本文引用:1]
[4] Zhou W, Yang H, Xie L, et al. Catena, 2021, 202: 105222. [本文引用:1]
[5] Pessanha S, Guilherme A, Carvalho M L. Applied Physics A, 2009, 97(2): 497. [本文引用:1]
[6] Marini F, Walczak B. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 153. [本文引用:1]
[7] JIANG Xiao-yu, LI Fu-sheng, WANG Qing-ya, et al(江晓宇, 李福生, 王清亚, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(5): 1535. [本文引用:1]
[8] Abdi H, Williams L J. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433. [本文引用:2]
[9] Chen C L P, Liu Z. IEEE Transactions on Neural Networks and Learning Systems, 2017, 29(1): 10. [本文引用:2]
[10] Chen C L P, Liu Z, Feng S. IEEE Transactions on Neural Networks and Learning Systems, 2018, 30(4): 1191. [本文引用:1]
[11] Wang J, Lyu S, Chen C L, et al. Journal of Intelligent Manufacturing, 2023, 34(4): 1779. [本文引用:1]
[12] Yang W, Li F, Zhao Y, et al. Analytical Methods, 2022, 14(40): 3944. [本文引用:2]
[13] QIAO Ji-hong, YUAN Xi-yan, WU Jing-zhu, et al(乔继红, 苑希岩, 吴静珠, 等). Journal of Food Safety & Quality(食品安全质量检测学报), 2023, 14(5): 9. [本文引用:1]
[14] Cheng J, Yu D, Yang Y. Mechanical Systems and Signal Processing, 2007, 21(3): 1197. [本文引用:1]
[15] Goh A T C. Artificial Intelligence in Engineering, 1995, 9(3): 143. [本文引用:1]