基于虚像相位阵列的光谱检测中角色散均匀性的研究

引用本文

纪文杰, 谭中伟. 基于虚像相位阵列的光谱检测中角色散均匀性的研究[J]. 光谱学与光谱分析, 2024,44(7): 1827-1834.
JI Wen-jie, TAN Zhong-wei. Research on Angular Dispersion Uniformity Based on the Virtual Image Phase Array Used in Spectral Detection[J]. Spectroscopy and Spectral Analysis, 2024,44(7): 1827-1834.
Doi:10.3964/j.issn.1000-0593(2024)07-1827-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于虚像相位阵列的光谱检测中角色散均匀性的研究

纪文杰, 谭中伟^*

北京交通大学电子信息工程学院光波技术研究所, 北京 100044

*通讯作者 e-mail: zhwtan@bjtu.edu.cn

作者简介: 纪文杰,女, 1995年生,北京交通大学电子信息工程学院硕士研究生 e-mail: 20120057@bjtu.edu.cn

收稿日期: 2022-11-21 修回日期: 2023-10-20

基金: 国家自然科学基金项目(61827818, 61875008)资助

摘要

随着光谱学的不断发展, 光谱检测作为一种快速无损的检测手段逐渐被应用于越来越多的领域中。而随着对信息精度要求的不断提高, 如何得到高分辨率和低波长误差的光谱信息, 是设计光谱检测系统时必须解决的问题。传统的色散元件如衍射光栅, 虽然有较大的波长响应范围, 但是通常只能提供nm量级的分辨率而无法满足当下的高光谱分辨率的要求。虚像相位阵列(VIPA)具有大角度色散特性, 可以有效提高系统的光谱分辨率, 因而近年来不断被用于精细光谱检测的研究。但其波长和色散角度对应关系存在非线性, 而且同一波长易产生多个衍射级次的光斑, 从而造成额外的光能损失。因此, 本文主要基于VIPA的交叉色散光路就如何降低VIPA色散的非均匀性的问题进行了理论分析和实验验证。首先基于傍轴理论的色散定律展开理论分析探讨了入射光腰尺寸、入射角度等参数对于VIPA色散的非线性程度和衍射级次数量的影响。然后通过进行仿真记录了宽光谱光源在不同VIPA倾斜角度条件下各波长衍射级次的数量, 以及各波长对应的光斑质心的坐标值。计算各情况下的质心坐标与拟合曲线之间的距离均差, 比较了不同角度条件下线性度的好坏。最后根据理论分析和仿真实验的结果进行实验。实验中记录了VIPA的交叉色散光路在不同的VIPA倾斜条件下出现的衍射级次数量, 并利用一个波长可变的激光器得到了不同波长的光源在VIPA倾斜2°的实验条件下各衍射级次光斑的质心坐标。同样通过计算不同衍射级次光斑的质心与拟合曲线之间的距离均差分析不同衍射级次的线性度好坏。实验证明通过控制入射光束参数, 可以一定程度上降低VIPA色散的非均匀性。 VIPA倾斜角度越大且越靠近探测器中央位置的衍射级次线性度越好。

关键词: 虚像相位阵列; 光谱检测; 线性度; 衍射级次

中图分类号:O433.1 文献标志码:A

Research on Angular Dispersion Uniformity Based on the Virtual Image Phase Array Used in Spectral Detection

JI Wen-jie, TAN Zhong-wei^*

Institute of Lightwave Technology, School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China

*Corresponding author

Abstract

As a fast and nondestructive detection method, spectral detection is gradually applied in more and more fields. With the continuous improvement of information accuracy requirements, obtaining spectral information with high resolution and low wavelength error is a primary challenge that researchers must face when designing spectral detection systems. Studying a new type of dispersive element becomes a feasible scheme. Traditional dispersive elements, such as diffraction gratings, have an extensive wavelength response range but usually can provide a resolution of the order of nm and cannot meet the requirements of the current hyperspectral resolution. Virtual Image Phased Array (VIPA) has the characteristics of large angular dispersion and high spectral resolution, which can effectively improve the spectral resolution of the system. Therefore, it has been continuously used in the research of fine spectral detection in recent years. However, the corresponding relationship between the wavelength and the dispersion angle is nonlinear, and the same wavelength is prone to generate multiple diffraction orders, resulting in additional light energy loss. Therefore, based on the cross-dispersion optical path of VIPA, this paper conducts theoretical analysis and experimental verification on how to reduce the dispersion nonuniformity of VIPA. Firstly, based on the dispersion law of paraxial theory, the influence of the incident waist size, incident angle and other parameters on the nonlinearity of VIPA dispersion and the number of diffraction orders is analyzed theoretically.The number of diffraction orders of each wavelength and the calibration value of the spot centroid corresponding to each wavelength of the broad spectrum light source at different VIPA tilt angles are recorded through simulation. The linearity under different angles is compared by calculating the average distance difference between the centroid coordinate and the fitting curve in each case. Finally, the experiment is carried out according to the theoretical analysis and the simulation results. The number of diffraction orders of the cross-dispersion optical path of VIPA under different VIPA tilt conditions was recorded in the experiment, and the centroid coordinates of each diffraction order spot of different wavelength light sources under the experimental condition of VIPA tilt of 2°are obtained by using a variable wavelength laser. Similarly, the linearity of different diffraction orders is analyzed by calculating the distance average between the centroid of different diffraction orders and the fitting curve. The results show that the nonuniformity of VIPA dispersion can be reduced to some extent by controlling the parameters of the incident beam.The larger the tilt angle of VIPA and the closer to the center of the detector, the better the diffraction order linearity.

Keyword: Virtual image phase array; Optical spectral analyzer; Linearity; Diffraction order

文章图片

引言

虚像相位阵列(virtually imaged phased array, VIPA)是一种新型的色散元件。相比于传统色散元件(如衍射光栅), VIPA具有更大的角度色散和更高的光谱分辨率^[1], 但与之伴随的问题是光谱级次重叠严重。 VIPA和衍射光栅组合的结构^[2], 使周期性混叠的光谱在与VIPA色散方向相垂直的方向进行了二次色散, 从而使光谱在二维空间展开, 极大地扩展了VIPA的应用前景。得益于其优秀的光学性能, 基于VIPA的高光谱分辨率仪器在多个领域得到应用, 如波分解复用^[3], 天文行星的物质信息检测^{[4, 5]}、激光雷达的二维光束控制^[6]、布里渊光谱成像^{[7, 8]}、光脉冲整形^[9]、相干层析成像^[10]以及高分辨率光谱仪^{[11, 12]}等。

VIPA的大角度色散特性使其在光谱检测领域得到了广泛应用, 但同一级次中波长与色散角之间的对应关系有一定的非线性^[3], 因此在应用中往往存在各种问题。例如, 当VIPA应用于光谱检测系统时, 这种非线性会导致系统测定波长和实际波长之间存在一定的误差; 应用在空间色散(如作为波分解复用)的相关领域中时, 会对光耦合造成困难, 造成额外的光能损失。目前为了减少这种非线性对系统的影响, 主要的解决方案可以分为两类: 第一类是通过改变光路中的元件或者参数使接收平面处的光斑尽可能均匀; 第二类是通过对获得光斑的坐标数据进行处理分析, 从而减少误差。

对第一种方案, 即改变光路参数虽然可以在一定程度实现VIPA色散光斑的均匀分布, 但也具有缺点。例如, 使用非球面反射镜代替普通的球面透镜^{[13, 14]}可以降低接收平面上的光斑分布的非均匀度。然而相对于球面镜来说, 非球面镜的设计相对复杂, 各个参数需要针对具体光路进行设计。而VIPA应用在波分解复用时, 也需要考虑色散均匀度的问题。使用非等间距光纤阵列可实现等信道间距波分复用^[15], 但需根据接收端平面的光强分布精准调整各光纤位置, 这对调试精准度提出了较高要求。因此该方法的优点在于可以使接收平面处的光斑位置具有较好的均匀性, 但也同时伴随着光路设计复杂化的问题。对于第二种方案, 即对光谱数据进行处理分析而使光谱数据误差减小的方法, 其优点在于对光路设计要求不高, 但在后期数据处理时, 为了获取更准确的波长对应关系需要更复杂的拟合算法。例如, 使用光频梳进行波长定标是目前研究人员经常使用定标方法之一^{[16, 17]}, 主要通过最小二乘拟合来确定光学频率与获取图像上的位置之间的关系。这种方法可使拟合精度大大提高, 但是在高精度光谱分析前提下, 波长定标精度在一定程度上受制于探测器本身像元大小和光学像差等因素。除了使用光频梳, 研究人员还通过电解质反射膜穿透深度与波长的关系的平滑性质, 修正波长信息中的误差^[18]。此外, 一种融合发散角与入射角的多峰叠加拟合公式, 也为波长定标和相关工艺发展提供了思路^[19]。所以, 寻找VIPA均匀色散条件的意义在于, 在保证不使色散光路复杂度增大和不使用过于复杂的拟合算法的同时尽可能的降低波长误差。

本文以光谱仪设计的实际需求出发, 比较和讨论了不同入射条件下, 经VIPA色散的波长的色散角度对应的线性关系; 在以降低不必要的光能损耗为目标, 分析了减少不必要的衍射级次时系统的构建需求。同时针对所提出的理论结果进行了仿真和实验, 验证了所提出理论的正确性。

1 原理与仿真

1.1 VIPA色散基本原理

VIPA作为一种新型的色散元件, 通过多光束干涉实现色散, 其结构及色散原理如图1(a)所示。 VIPA的色散情况受到自身倾斜角度、介质折射率、厚度、透镜焦距和高斯光束束腰尺寸等因素的影响。这些因素一方面影响VIPA角色散率大小, 另一方面影响出现的衍射级次数量。如果出现的衍射级次数量越多, 则在总体上二维光谱的光斑分布的线性度越差^[20], 并且会导致更多的能量损耗^[21]。为了尽量减少二维光谱的能量损失但同时又保证光源的所有波长都在二维平面上有映射光斑, 需要对VIPA以及入射高斯光束尺寸等参数做出一系列的约束。

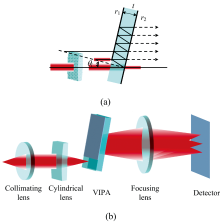	Figure Option View Download New Window
	图1 VIPA色散原理光路图 (a): VIPA基本原理; (b): VIPA色散光路Fig.1 Schematic of the VIPA system (a): Fundamentals of VIPA; (b): The systematic optical path of VIPA

VIPA的一维色散光路如图1(b)所示, 由准直透镜、聚焦柱面镜、 VIPA、成像透镜和探测器组成, 探测器位于成像透镜的后焦平面上^[22]。目前对VIPA色散规律的描述^{[23, 24, 25, 26]}中, 接受程度最广的是基于傍轴理论的色散定律。该理论由菲涅尔衍射积分公式^[26]出发, 最终得到经由VIPA色散的各波长的光斑在成像透镜后焦平面上的光场强度分布。使用该理论分析VIPA的色散定律主要有两点原因: 首先, 在VIPA的色散光路中, 成像透镜的焦距远大于实验所用的光波波长, 且探测器位于透镜后焦平面而远离衍射孔径; 这两点符合标量衍射理论的适用条件。此外, 研究人员已经通过实验验证了在小入射角的情况下, 使用该方法计算得到的理论值和实验值比较一致, 相比于平面波色散定律具有更精确的效果。因此使用该理论分析VIPA的色散规律是合理的。由该理论得到的光场强度分布可以由式(1)表达

$\begin{array}{l} I_{out} (x_{F}, λ) \propto \exp (- \frac{2 f_{1}^{2} x_{F}^{2}}{f_{2}^{2} W^{2}}) \times \\ \frac{1}{(1 - r_{1} r_{2})^{2} + 4 (r_{1} r_{2}) si n^{2} (kΔ / 2)} \end{array}$ (1)

式(1)中, $Δ = [2 tn \cos (θ_{in}) - 2 t \tan (θ_{in}) \cos \cos (θ_{i}) θ_{λ} - \frac{t \cos (θ_{in}) θ_{λ}^{2}}{n}],$ 其中 $x_{F}$ 为光斑在透镜后焦平面上距离光轴在x方向上的距离, W为入射到柱面镜的高斯光束束腰半径, $f_{1}$ 为聚焦柱面镜焦距, $f_{2}$ 为球面成像透镜焦距。 $t$ 为VIPA的厚度, n为VIPA介质的折射率, θ_i为VIPA倾斜角度, 也是光束注入VIPA的入射角, r₁和r₂分别是VIPA前后表面薄膜反射率, θ_in为光束进入VIPA介质后的折射角, 且θ_i和θ_in符合斯涅尔定律, 即 $n \cdot \sin \sin (θ_{in}) = \sin \sin (θ_{i}) 。 θ_{λ}$ 代表波长为 $λ$ 的光经VIPA出射后的色散角, 由傍轴条件可知: θ_λ≈ x_F/f₂。

为了方便分析可将I_out看作是I_a和I_b的乘积, 其中

$I_{a} = \exp (- \frac{2 f_{1}^{2} x_{F}^{2}}{f_{2}^{2} W^{2}})$ (2)

$I_{b} = \frac{1}{(1 - r_{1} r_{2})^{2} + 4 (r_{1} r_{2}) si n^{2} (kΔ / 2)}$ (3)

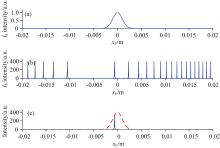
如图2所示, I_a为一高斯型曲线, 当入射光束为单色光, 在一定的VIPA初始条件下, 各个衍射级次的强度包络曲线由I_a决定, 而具体的各个衍射级次的空间位置则由I_b决定。当光源包含多个波长成分时, 由于I_a并不受波长影响, 所以总体的强度曲线包络仍为高斯曲线。由此分析过程可知, 可以通过控制I_a和I_b的相对关系, 来控制各个波长出现的衍射级次数量以及坐标位置。

	Figure Option View Download New Window
	图2 包络与出现衍射级次数量的关系 (a): 高斯包络; (b): 各级次的位置; (c): 包络与各级次强度的关系Fig.2 The relationship between the envelope and the number of diffraction orders (a): Gaussian-shape envelope; (b): Position of diffraction orders; (c): Relationship between envelope and strength of different orders

1.2 单衍射级次的参数要求

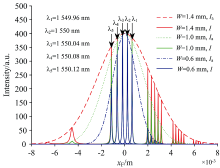
根据VIPA的色散强度公式可知, 在不同的条件下出现的衍射级次不同。根据高斯曲线的特性, 当改变式(2)中f₁/f₂W的值时, 曲线包络的集中程度会发生改变。如图3所示, 蓝、绿、红三色曲线分别代表W为0.6、 1和1.4 mm时光源波长范围为1 549.96~1 550.12 nm时的光强分布曲线。当W越大(f₁/f₂W越小)时, 包络曲线的集中程度越差, 这导致同一波长出现越多的衍射级次。

	Figure Option View Download New Window
	图3 不同高斯光束尺寸下的衍射级次数量Fig.3 Number of diffraction orders for different Gaussian beam sizes

为了尽可能地减少不必要的衍射级次出现, 需要根据VIPA的自由光谱范围(free spectral range, FSR)来设计I_a中各参数, 从而控制窗口大小。通过计算接收平面上最上端的坐标和最下端的坐标, 可得这两个位置上对应的衍射角角度。由此角度结合VIPA角度和波长的对应公式, 即可求得在当前条件下, 在同一级次上窗口允许通过的波长范围。此范围应略大于FSR的范围。根据高斯曲线的性质, 该包络曲线关于x_F=0轴对称, 同时考虑到光路中由于通过透镜介质和在空气中传播时造成的损耗, 到达探测器时光斑的实际功率应小于理论值。因此将I_a的窗口范围选择在 $(- A \frac{f_{2} W}{2 f_{1}}, A \frac{f_{2} W}{2 f_{1}})$ , 其中A定义为一个包络系数。 A值大小与实验中具体条件有关, 如具体损耗和探测器性能指标等。在本文中, 通过分析A值的大小获得位置在最上端和最下段的光斑位置。由傍轴条件, 可得到在这两个位置上对应的角度分别是θ₁≈ -A $\frac{W}{2 f_{1}}$ , θ₂≈ A $\frac{W}{2 f_{1}}$ 。

由波长与角度的对应关系^[27]可得到对应于边界位置的两个波长λ₁和λ₂。则VIPA窗口允许通过的同一级次的波长范围为

$\begin{array}{l} λ_{1} - λ_{2} = A λ_{0} \frac{W \tan (θ_{in}) \cos (θ_{i})}{f_{1} n \cos (θ_{in})} ~ \\ λ_{1} - λ_{2} = A λ_{0} \frac{W θ_{i}}{f_{1} n^{2}} \end{array}$ (4)

式(4)中, $m λ_{0} = 2 tn \cos (θ_{in}), n \cdot \sin (θ_{in}) = \sin (θ_{i}) 。$ 一般θ_i和θ_in很小。

由前文的分析可知, 包络满足高斯型曲线导致处于边缘的光斑强度较低, 不利于实际的具体应用。因此式(4)所代表的波长范围应略大于FSR, 小于两倍的FSR。若以λ_FSR表示一个FSR的波长范围

$λ_{FSR} = \frac{c}{[2 tn \cos (θ_{in}) - 2 t \tan (θ_{in}) \cos (θ_{i}) θ_{λ}^{2} - \frac{t \cos (θ_{in}) θ_{λ}^{2}}{n}]}$ (5)

根据波长与衍射角度的对应关系, 对其求导, 可知其角色散公式如式(6)

$\frac{d θ_{λ}}{\frac{d λ_{p}}{λ_{0}}} = - \frac{1}{\frac{\sin (2 θ_{i})}{2 [n_{r}^{2} - si n^{2} (θ_{i})]} + \frac{θ_{λ}}{n_{r}^{2}}}$ (6)

由式(6)分析可知, VIPA色散均匀度需考虑到入射角、材料的折射率以及波长的影响。其中色散的不均匀性主要来自于分母中的二次项θ_λ/ $n_{r}^{2}$ , 若要降低此项对整体的影响, 应选择折射率大的材料或是使θ_i在合理范围内取较大值。

首先通过公式计算讨论较为合理的A的取值。计算使用的参数分别为: θ_i=1.8°, n~1.5, t=2.5 mm, f₁=60 mm, f₂=200 mm。通过改变不同的高斯光束尺寸来改变强度曲线包络的通过窗口, 利用结果讨论不同情况下的衍射级次出现的情况并得到相对合理的A值。分别将A取值为3, 2.5, 2, 1.5, 1, 0.5时利用式(1)即可求得各波长光斑在探测器表面的坐标位置如图4所示。

	Figure Option View Download New Window
	图4 不同A值下的波长与坐标的对应关系 (a): A=3; (b): A=2.5; (c): A=2; (d): A=1.5; (e): A=1; (f): A=0.5Fig.4 Correspondence between wavelength and coordinate under different A values (a): A=3; (b): A=2.5; (c): A=2; (d): A=1.5; (e): A=1; (f): A=0.5

根据结果发现: A值过大时部分波长无法映射在探测器上; 当A值过小时同一波长会出现多个衍射级次, 造成光能损失。因此当A值取为1到2之间的范围时较为合理。此时虽然有部分波长出现了两个衍射级次光斑, 但考虑到越远离探测器中心的光强越弱, 单纯追求仅出现单个衍射级次可能导致部分波长的光由于强度太弱而导致检测到信号的信噪比过低, 造成误差或光谱检测的灵敏度降低。因此, 在利用二维光谱展开的光谱检测中, 牺牲掉部分光斑的光强是可以接受的, 这样可以保证有一个完整的周期出现在检测平面上, 如图3中绿色曲线所示。本次实验中将A取值为1.5。

1.3 线性条件分析

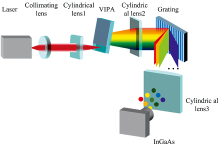
在之前的理论分析过程中已经讨论了入射的高斯光束的光腰尺寸对出现的衍射级次数量的影响, 为了进一步分析其他入射光束参数对光斑分布的影响, 使用ZEMAX对多波长光源进行仿真。光路设置如图5(a)所示: 球面镜准直后的光束通过柱面镜在x方向上聚焦, 从而耦合进VIPA色散。经VIPA色散后的不同波长的光由光栅进行交叉色散, 经球透镜聚焦成像在探测平面, 得到二维色散图样[图5(b)]。由式(6)可知, 入射角会对角色散产生影响, 因此通过仿真, 分别记录了VIPA倾斜角度在1.4°、 1.6°、 1.8°、 2°时波长范围为1 549.92~1 550.2 nm的各光斑的坐标值, 结果如图6所示, 由该坐标分布结果可看出。倾斜角度为1.4°时, 此时强度包络过窄, 因此波长1 549.96 nm的光在探测器上没有相应的光斑对应, 导致所得的光谱与真实光谱不一致而形成误差。对比其余3组的实验结果并通过分析式(3)可知, 随着倾斜角度的增大, 各波长光斑分布的更加密集, 出现的衍射级次逐渐增多。

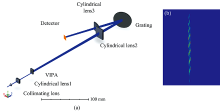	Figure Option View Download New Window
	图5 ZEMAX仿真图 (a): 装置图; (b): 探测器上的光斑分布Fig.5 Schematic of the ZEMAX simulation experiment (a): The setup of the VIPA spectral dispersion; (b): Spot distribution on the detector

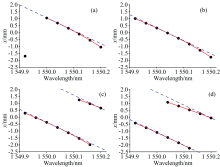	Figure Option View Download New Window
	图6 不同入射角度下的各波长坐标分布 (a): θ_i=1.4°; (b): θ_i =1.6°; (c): θ_i=1.8°; (d): θ_i =2°Fig.6 Distribution of wavelengths at different incidence angles (a): θ_i=1.4°; (b): θ_i =1.6°; (c): θ_i=1.8°; (d): θ_i =2°

将得到的各波长和坐标位置进行曲线拟合并对拟合曲线作切线, 切点横坐标为1 550.04 nm。通过求各波长在接收平面处的坐标x_λ和切线在该波长处的纵坐标值x_λt间的距离均值判断拟合曲线的线性程度, 距离均值越大表示坐标点距离切线总体距离越远, 即线性度越差。计算公式如式(7), 式中E_θ表示实验中不同倾斜角度下的距离均值, N表示实验中参与计算的光斑点数。由于倾斜角度为1.4°时部分波长无对应光斑, 因此本次计算仅考虑1.6°、 1.8°和2.0°时距离均值情况。根据式(7)获得的计算结果如表1所示。

$E_{θ} = \frac{\sum (x_{λ} - x_{λt})}{N}$ (7)

表1 不同入射角下光斑坐标与切线对应坐标差值的平均值 Table 1 The mean value of the difference between the spot coordinate and the tangent corresponding coordinate at different incident angles

由表1中数据可知, 若将所有光斑都加入计算, 则2.0°的线性度最差, 1.6°次之, 1.8°时线性度最佳; 如果仅考虑单个衍射级次而将大于1个衍射级次的部分光斑排除在外, 则2.0°时的线性度最佳。这与角度变大时, 其角色散率相对较小有关。

在角度对线性度影响的仿真实验中, 在较大的角度下衍射级次的数量明显增多, 这与改变W/f₁的效果类似。仅改变W/f₁值时, 不会改变各级次强度最大值本身的位置, 因此仅考虑包络边界值与高衍射级次的相对位置即可。然而当改变VIPA倾斜角度时, 改变了相位条件, 使各光斑在探测器平面的相对位置也发生改变。同时, 改变倾斜角度会导致式(4)中一次项的系数大小, 从而影响VIPA的角色散率。倾斜角度越大, 虽然其线性程度较好, 但此时较小的角色散率会导致系统整体的色散效果较差, 制约其光谱分辨率的提高。且在倾斜角度较大时, 需配合单衍射级次条件对高斯光束光腰尺寸做出调整以控制光斑数量, 从而避免过多的光能损失。而角度较小时, 虽然此时同一波长不会出现较多衍射级次, 但是可能出现部分波长的光斑缺失, 或是由于远离中心位置的光斑强度过低而造成探测器无法识别的情况。

2 实验与结果讨论

根据前文的理论分析和仿真结果进行实验, 各元件摆放如图7所示。实验使用的光源是一个波长可变的激光器, 型号为HP 8164A。激光器通过一个光纤准直器输出激光, 光束直径约1 mm, 经由一个焦距为50 mm的柱面镜会聚后注入厚度为2.4 mm、尺寸为25.4 mm的VIPA。 VIPA输出光在x方向展开后, 光束由Newport 1 100线·mm^-1的衍射光栅在y方向展开。 VIPA和光栅的傅里叶透镜焦距分别为200和150 mm。将Xenics公司的XC130红外成像系统置于光栅傅里叶透镜的后焦平面上用于采集光斑图像。其像素数为320×256, 总面积为9.6 mm×7.6 mm, 像素间距为30 μm×30 μm。

	Figure Option View Download New Window
	图7 实验装置图Fig.7 Experimental setup diagram

实验过程中通过调整VIPA的倾斜角度改变θ_i。在θ_i~1°和θ_i~1.5°的条件下, 将光束输入色散系统进行色散, 探测器接收到的光斑图样分别如图8(a)和(b)所示。由实验结果可知: 在保持高斯光束尺寸不变的条件下, θ_i越大时出现的衍射光斑越多, 同时不同级次间光斑的空间距离缩短。

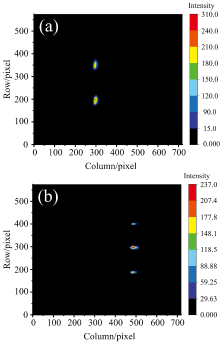	Figure Option View Download New Window
	图8 小入射角度较小时不同波长光斑的成像 (a): θ_i~1°; (b): θ_i~1.5°Fig.8 Imaging of facula with different wavelengths when the incidence angle is small (a): θ_i~1°; (b): θ_i~1.5°

为了进一步验证入射角度对于衍射级次数量及其对于线性度的影响, 继续调整VIPA倾斜角度, 在θ_i~2°条件下分别将不同波长的光注入光路。光束经过VIPA和衍射光栅的色散, 在一段时间内通过InGaAs面阵收集到对应的光强数据。图9(a)—(c)是将实验过程中采集到的多组数据其中的3组整理得到的图像。由图9可以观察到, 在此时的光路设置下, 同一个波长可以产生3到4个衍射级次, 与θ_i~1.5°条件下的实验结果相比产生了更多的衍射级次; 并且光斑的位置随着入射波长的变化而变化。

	Figure Option View Download New Window
	图9 不同波长下InGaAs面阵采集到的光斑数据Fig.9 Data collected by InGaAs array at different wavelength

将θ_i ~2°条件下收集到的所有数据进行处理, 并计算不同时间下光斑质心的坐标位置, 整理结果如图10所示。其中横坐标为波长的变化量, 纵坐标表示光斑的坐标, 黑色点为每个时刻出现的光斑的质心, 红色实线是对光斑质心坐标进行线性拟合的结果。进一步对拟合曲线在波长变化量为1.5 nm处求其切线, 以蓝色虚线表示。将不同衍射级次的光斑从上至下进行标号, 并分别分析不同衍射级次下线性度的好坏。

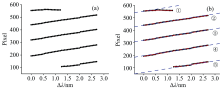	Figure Option View Download New Window
	图10 光斑质心变化及线性拟合 (a): 质心坐标; (b): 坐标线性拟合Fig.10 Variation and linear fitting of light spot centroid (a): Coordinate of centroid; (b): Linear fitting of coordinate

通过计算不同级次下各波长光斑坐标与切线的距离均值E对比各级次得线性度好坏, 计算方式与式(7)一致, 计算后得到的结果如表2所示。分析表2中的计算结果可知, 出现的衍射级次中, 标号为3的级次的距离均值最小, 表明其线性度较好; 而越靠近探测器边缘, 级次的线性度越差。其中同时由于包络调制的影响, 其光斑强度也越小。

表2 各衍射级次的距离均值 Table 2 Mean value of distance of different diffraction orders

除了角度和高斯光束尺寸的影响, 介质折射率对波长与位置的关系也具有一定影响。从式(4)可以看出, 影响坐标位置非线性的原因主要是因为存在一个二次项。当VIPA介质折射率越大时, 此二次项对整体的色散关系影响越小, 线性程度越好。同理, 此分析也适用于前文提到过的倾斜角度过大时的情况。因为当角色散较小时, θ_λ作为一个很小的数值, 其二次项也可以在一定程度上忽略, 此时可大致将色散关系看作一个仅与VIPA倾斜角度有关的一次函数。

3 结论

尽可能地减少VIPA色散的非均匀度对于进一步提高波长标定精度的准确性具有重要影响。根据理论分析, 入射光束光腰尺寸、入射角度和VIPA介质折射率等因素均会对VIPA的色散均匀性产生一定的影响。经仿真和实验验证得到以下结论: 通过控制入射的高斯光束尺寸和柱面镜焦距等因素, 可以控制各波长出现的衍射级次数量; 入射角度较大时, 色散的均匀程度较好, 但出现的衍射级次数量增多, 且角色散率有所降低; 同时出现多个衍射级次的情况下, 位于中心位置的级次线性度更好。因此实际应用时, 可以通过选择介质折射率较大的VIPA, 用合理范围内相对较大的倾斜角度实现较好的色散均匀度。同时可以通过控制入射光束尺寸和柱面镜焦距减少衍射级次数量, 避免出现不必要的衍射级次, 减少光能损失。

参考文献

文献列表

[1]	Shirasaki M. Optics Letters, 1996, 21(5): 366. [本文引用:1]
[2]	Xiao S J, Weiner A M. Optics Express, 2004, 12(13): 2895. [本文引用:1]
[3]	Xiao S J, Weiner A M, Lin C. Journal of Lightwave Technology, 2005, 23(3): 1456. [本文引用:2]
[4]	Bourdarot G, Le Coarer E, Alecian E, et al. International Conference on Space Optics—ICSO, 2016, 105622D(2017). [本文引用:1]
[5]	Zhu X, Lin D, Hao Z, et al. The Astronomical Journal, 2020, 160(3): 135. [本文引用:1]
[6]	Li Z, Zang Z, Han Y, et al. Optics Express, 2021, 29(11): 16547. [本文引用:1]
[7]	Fiore A, Zhang J, Shao P, et al. Applied Physics Letters, 2016, 108(20): 203701. [本文引用:1]
[8]	Fiore A, Scarcelli G. Biomedical Optics Express, 2019, 10(3): 1475. [本文引用:1]
[9]	Supradeepa V R, Huang C B, Leaird D E, et al. Optics Express, 2008, 16(16): 11878. [本文引用:1]
[10]	Bao W, Ding Z, Li P, et al. Optics Express, 2014, 22(8): 10081. [本文引用:1]
[11]	Berghaus K, Zhang J, Yun S H, et al. Optics Letters, 2015, 40(19): 4436. [本文引用:1]
[12]	Roberts F C, Lewand owski H J, Hobson B F, et al. Molecular Physics, 2020, 118(16): e1733116. [本文引用:1]
[13]	Ooi H, Nakamura K, Akiyama Y, et al. Journal of Lightwave Technology, 2002, 20(12): 2196. [本文引用:1]
[14]	Nugent-Gland orf L, Neely T, Adler F, et al. Optics Letters, 2012, 37(15): 3285. [本文引用:1]
[15]	Xiao S J, Weiner A M. IEEE Photonics Technology Letters, 2005, 17(2): 372. [本文引用:1]
[16]	Hébert N B, Scholten S K, White R T, et al. Optics Express, 2015, 23(11): 13991. [本文引用:1]
[17]	Scholten S K, Anstie J D, Hébert N B, et al. Optics Letters, 2016, 41(6): 1277. [本文引用:1]
[18]	HAO Zhi-bo, YE Hui-qi, TANG Liang, et al(郝志博, 叶慧琪, 唐靓, 等). Acta Optica Sinica(光学学报), 2022, 42(1): 0112002. [本文引用:1]
[19]	WANG Qiao-yun, YANG Jing, GAO Xin-yu, et al(汪巧云, 杨静, 高欣宇, 等). Acta Optica Sinica(光学学报), 2021, 41(4): 0412001. [本文引用:1]
[20]	Tan Z, Ren W, Liu Z, et al. Applied Optics, 2014, 53(23): 5259. [本文引用:1]
[21]	TAN Zhong-wei, CHEN Zhi-wei, SHEN Xiao-xiao, et al(谭中伟, 陈志伟, 沈笑笑, 等). Infrared and Laser Engineering(红外与激光工程), 2013, 42(S01): 123. [本文引用:1]
[22]	Xiao S J, Weiner A M. Conference on Lasers and Electro-Optics (CLEO), June06-06, 2003, Baltimore, MD, USA. New York: IEEE, 8424342. [本文引用:1]
[23]	Vega A, Weiner A M, Li C. Applied Optics, 2003, 42(20): 4152. [本文引用:1]
[24]	Xiao S J, Weiner A M, Lin C. IEEE Journal of Quantum Electronics, 2004, 40(4): 420. [本文引用:1]
[25]	Weiner A M. Applied Optics, 2012, 51(34): 8187. [本文引用:1]
[26]	Hu X, Sun Q, Li J, et al. Optics Express, 2015, 23(1): 1. [本文引用:2]
[27]	Joseph W Goodman, Introduction to Fourier Optics(傅里叶光学导论). 4th Edition(第4版). Translated by CHEN Jia-bi, QIN Ke-cheng, CAO Qi-zhi(陈家璧, 秦克诚, 曹其智, 译). Beijing: Science Press(北京: 科学出版社) 2020. 77. [本文引用:1]

1996

0.0

... 相比于传统色散元件(如衍射光栅), VIPA具有更大的角度色散和更高的光谱分辨率^[1], 但与之伴随的问题是光谱级次重叠严重 ...

2004

0.0

... VIPA和衍射光栅组合的结构^[2], 使周期性混叠的光谱在与VIPA色散方向相垂直的方向进行了二次色散, 从而使光谱在二维空间展开, 极大地扩展了VIPA的应用前景 ...

2005

0.0

... 得益于其优秀的光学性能, 基于VIPA的高光谱分辨率仪器在多个领域得到应用, 如波分解复用^[3], 天文行星的物质信息检测^[4,5]、激光雷达的二维光束控制^[6]、布里渊光谱成像^[7,8]、光脉冲整形^[9]、相干层析成像^[10]以及高分辨率光谱仪^[11,12]等 ...

... VIPA的大角度色散特性使其在光谱检测领域得到了广泛应用, 但同一级次中波长与色散角之间的对应关系有一定的非线性^[3], 因此在应用中往往存在各种问题 ...

2016

0.0

2020

0.0

2021

0.0

2016

0.0

2019

0.0

2008

0.0

2014

0.0

2015

0.0

2020

0.0

2002

0.0

... 例如, 使用非球面反射镜代替普通的球面透镜^[13,14]可以降低接收平面上的光斑分布的非均匀度 ...

2012

0.0

... 例如, 使用非球面反射镜代替普通的球面透镜^[13,14]可以降低接收平面上的光斑分布的非均匀度 ...

2005

0.0

... 使用非等间距光纤阵列可实现等信道间距波分复用^[15], 但需根据接收端平面的光强分布精准调整各光纤位置, 这对调试精准度提出了较高要求 ...

2015

0.0

... 例如, 使用光频梳进行波长定标是目前研究人员经常使用定标方法之一^[16,17], 主要通过最小二乘拟合来确定光学频率与获取图像上的位置之间的关系 ...

2016

0.0

2022

0.0

... 除了使用光频梳, 研究人员还通过电解质反射膜穿透深度与波长的关系的平滑性质, 修正波长信息中的误差^[18] ...

2021

0.0

... 此外, 一种融合发散角与入射角的多峰叠加拟合公式, 也为波长定标和相关工艺发展提供了思路^[19] ...

2014

0.0

... 如果出现的衍射级次数量越多, 则在总体上二维光谱的光斑分布的线性度越差^[20], 并且会导致更多的能量损耗^[21] ...

2013

0.0

... 如果出现的衍射级次数量越多, 则在总体上二维光谱的光斑分布的线性度越差^[20], 并且会导致更多的能量损耗^[21] ...

0.0

... VIPA的一维色散光路如图1(b)所示, 由准直透镜、聚焦柱面镜、 VIPA、成像透镜和探测器组成, 探测器位于成像透镜的后焦平面上^[22] ...

2003

0.0

... 目前对VIPA色散规律的描述^{[23,24,25,26]}中, 接受程度最广的是基于傍轴理论的色散定律 ...

2004

0.0

... 目前对VIPA色散规律的描述^{[23,24,25,26]}中, 接受程度最广的是基于傍轴理论的色散定律 ...

2012

0.0

... 目前对VIPA色散规律的描述^{[23,24,25,26]}中, 接受程度最广的是基于傍轴理论的色散定律 ...

2015

0.0

... 目前对VIPA色散规律的描述^{[23,24,25,26]}中, 接受程度最广的是基于傍轴理论的色散定律 ...

... 该理论由菲涅尔衍射积分公式^[26]出发, 最终得到经由VIPA色散的各波长的光斑在成像透镜后焦平面上的光场强度分布 ...

2020

0.0

... 由波长与角度的对应关系^[27]可得到对应于边界位置的两个波长#cod#x003bb ...