草甸草原植物beta多样性高光谱遥感估算方法

引用本文

杨星晨, 雷少刚, 徐军, 苏兆瑞, 王维忠, 宫传刚, 赵义博. 草甸草原植物beta多样性高光谱遥感估算方法[J]. 光谱学与光谱分析, 2024,44(6): 1751-1761.
YANG Xing-chen, LEI Shao-gang, XU Jun, SU Zhao-rui, WANG Wei-zhong, GONG Chuan-gang, ZHAO Yi-bo. Estimation of Plants Beta Diversity in Meadow Prairie Based on Hyperspectral Remote Sensing Technology[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1751-1761.
Doi:10.3964/j.issn.1000-0593(2024)06-1751-11 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

草甸草原植物beta多样性高光谱遥感估算方法

杨星晨¹, 雷少刚^1,^*, 徐军², 苏兆瑞³, 王维忠³, 宫传刚⁴, 赵义博¹

1. 中国矿业大学矿山生态修复教育部工程研究中心, 江苏徐州 221116

2. 内蒙古农业大学草原与资源环境学院, 内蒙古呼和浩特 010011

3. 内蒙古准格尔旗矿区事业发展中心, 内蒙古鄂尔多斯 017100

4. 安徽理工大学空间信息与测绘工程学院, 安徽淮南 232001

*通讯作者 e-mail: lsgang@126.com

作者简介: 杨星晨, 1995年生, 中国矿业大学矿山生态修复教育部工程研究中心博士研究生 e-mail: TB21160018B4@cumt.edu.cn

收稿日期: 2022-10-21 修回日期: 2023-10-15

基金: 国家重点研发计划项目(2023YFF1306005), 鄂尔多斯科技合作重大专项(2021EEDSCXQDFZ010)资助

摘要

目前, 全球生物多样性的状态非常堪忧, 因此, 利用光谱技术估算生物多样性成为了生态学家和遥感学家共同关注的热点。目前关于植物alpha多样性的研究很多, 而关于beta多样性的研究较少, 仍存在一些问题值得去探索。为了探究利用遥感技术估算植物beta多样性的最佳光谱指数以及最佳影像空间分辨率, 以草甸草原为研究区, 基于无人机高光谱遥感影像, 从光谱距离、光谱角度、生物多样性概念三个方面计算了6种beta多样性估算指数(4种为我们构建的新指数, 2种为已有的指数), 并采用Mantel tests和相关系数筛选最佳的光谱指数。然后将筛选出来的指数应用于不同空间分辨率的影像, 以期得到最佳观测尺度。另外, 为了提高指数的估算能力, 对比了一阶导数变换和Savitzky-Golay滤波两种光谱变换方法, 以及相关系数法、连续投影法、竞争性自适应重加权法三种特征波段选择方法。结果表明, 不论是采用亚尺度观测(像元大小<样方大小)还是等尺度观测(像元大小=样方大小), 最佳的光谱指数均为光谱距离指数, 且光谱距离指数在不同影像空间分辨率下均表现良好。在草原地区, 当影像空间分辨率约为0.25 m时, 该指数可以取得最佳的估算结果。经一阶导数变换并用相关系数法提取特征波段后构建的光谱距离指数与beta多样性拥有最强的相关性, 今后可利用该指数构建估算模型或者直接表征beta多样性。该研究对于科学的选取光谱指数和影像空间分辨率去估算植物beta多样性具有一定的指导意义。

关键词: beta多样性; 高光谱遥感; 光谱指数; 观测尺度; 光谱曲线

中图分类号:TP79 文献标志码:A

Estimation of Plants Beta Diversity in Meadow Prairie Based on Hyperspectral Remote Sensing Technology

YANG Xing-chen¹, LEI Shao-gang^1,^*, XU Jun², SU Zhao-rui³, WANG Wei-zhong³, GONG Chuan-gang⁴, ZHAO Yi-bo¹

1. Engineering Research Center of Ministry of Education for Mine Ecological Restoration, China University of Mining and Technology, Xuzhou 221116, China

2. College of Grassland, Resources and Environment, Inner Mongolia Agricultural University, Huhhot 010011, China

3. Inner Mongolia Jungar Banner Mining Area Development Center, Ordos 017100, China

4. College of Spatial Information and Surveying Engineering, Anhui University of Science & Technology, Huainan 232001, China

*Corresponding author

Abstract

Due to global biodiversity loss, the estimation of biodiversity using spectral technology has become a hot topic for ecologists and remote sensing scientists. There are many studies on alpha diversity but few studies on beta diversity. There are still some problems worth exploring. To explore the best spectral index and image spatial resolution for estimating plant beta diversity using remote sensing technology, this paper took meadow grassland as the research area. It calculated six beta diversity estimation indices from three aspects: spectral distance, spectral angle and biodiversity concept based on UAV hyperspectral remote sensing images. We developed four indices, and two are existing indices. Mantel tests and correlation coefficients were used to select the best spectral index. Then, the selected index was applied to images with different spatial resolutions to obtain the best observation scale. In addition, to improve the estimation ability of the index, this paper compared two spectral transformation methods, the first derivative transform and Savitzky-Golay filter, and three feature band selection methods: correlation coefficient, successive projections algorithm and the competitive adaptive reweighted sampling. The results showed that in both subscale observation (pixel size<quadrat size) and equal scale observation (pixel size=quadrat size), the best spectral index was the spectral distance index, and the spectral distance index performed well under different image spatial resolutions. The best estimation result can be obtained in the grassland area when the image spatial resolution is about 0.25 m. The spectral distance index constructed after the first derivative transformation and extraction of characteristic bands by the correlation coefficient method has the strongest correlation with beta diversity. In the future, this index can be used to build estimation models or directly indicate beta diversity. This paper has guiding significance for scientifically selecting spectral index and image spatial resolution to estimate plant beta diversity.

Keyword: Beta diversity; Hyperspectral remote sensing; Spectral index; Observation scale; Spectral curve

文章图片

引言

生物多样性是生态系统的主导功能, 是水源涵养、土壤保持、气候调节等功能得以实现的基础^[1]。然而, 由于景观破碎化和气候变暖等原因, 全球生物多样性正在急剧减少。生物多样性的快速估算对于生物多样性保护工作具有重要意义。目前, 光谱技术被广泛用于植物多样性的快速估算^[2]。

生物多样性包括alpha多样性和beta多样性。 alpha多样性为群落内多样性, 旨在测度群落内物种的丰富程度; beta多样性为群落间多样性, 旨在描述群落之间物种组成的差异。在评估alpha多样性方面, 遥感技术取得了较好的进展。不论是直接法^[3]还是间接法^[4], 都有许多成功的案例。然而, 利用遥感技术估算beta多样性的研究却很少, 仍存在一些问题值得去探索。

首先是缺乏较好的光谱指数。利用遥感技术估算beta多样性的关键是如何利用光谱去测度两个群落之间物种组成的差异, 并提出可靠的指数来表示这种差异, 或者进一步用该指数构建估算模型。例如, 经典的NDVI(normalized difference vegetation index)指数被认为与植被覆盖度具有很强的相关性, 并被广泛用于直接表征植被覆盖度^[5]或构建植被覆盖度估算模型^[6]。对于alpha多样性, 光谱变异系数被认为与群落内物种丰富度具有强相关性, 大量研究用光谱变异系数的大小来表示alpha多样性的高低^{[7, 8]}。然而对于beta多样性, 目前尚无得到广泛认可的光谱指数可以用来指示beta多样性。另外, 构建光谱指数时存在两种情况: 等尺度观测(像元大小=样方大小)和亚尺度观测(像元大小< 样方大小), 其区别在于可利用的光谱曲线数量不同(图1)。彭羽等^[9]利用手持式地物光谱仪研究了如何估算植物物种beta多样性, 并构建了一些较好的指数。但是手持式地物光谱仪针对一个样方只能生成一条光谱曲线, 因此我们有必要探索: 如何运用多条光谱曲线的信息构建光谱指数以及最佳的光谱指数是什么?

	Figure Option View Download New Window
	图1 样方、影像空间分辨率及光谱曲线数量间的对应关系Fig.1 The corresponding relationship between quadrat, image spatial resolution and the number of spectral curves

其次是尚不清楚最佳的影像空间分辨率是多少。尺度问题一直是遥感研究中的热点。针对alpha多样性的遥感估算, 多位学者研究了最佳空间分辨率的问题。 Wang^[7]等认为估算草原植物多样性时像元空间分辨率不应低于10 cm, 而Gholizadeh等^[4]同样以草原为研究对象, 发现影像空间分辨率为1 m时, 光谱指数与alpha多样性仍具有很好的相关性。但是目前缺乏关于beta多样性的尺度问题的研究, 因此我们有必要探索: 利用遥感技术估算草原植物beta多样性时最佳的影像空间分辨率是多少。

为了回答上述两个问题, 首先从光谱距离、光谱角度、生物多样性概念三个方面计算了6种beta多样性光谱指数, 并采用曼特尔检验(Mantel tests)和相关系数筛选最佳光谱指数。然后将筛选出来的指数应用于不同空间分辨率的影像, 以期得到最佳观测尺度。

1 实验部分

1.1 研究区概况

研究区位于内蒙古自治区呼伦贝尔草甸草原。研究区土壤类型为暗栗钙土, 调查时期的平均植被覆盖度为70%。由于临近宝日希勒煤矿, 因此该草原受到采矿活动的扰动, 群落组成的空间异质性较大, 适合进行植物beta多样性研究。

1.2 植物多样性调查

植被调查样方采用传统的1 m× 1 m大小, 共有25个调查样方, 调查内容为样方内物种的数量及每个物种的株数。调查结束后在样方的四个角点以及中心点定位, 定位精度为2 cm。 beta多样性指数选择Bray-Curtis指数, 该指数采用数量数据测度法, 既考虑某个物种存在与否又考虑其个体数目。 Bray-Curtis指数的计算公式为

$Bray⁃Curtis = 1 - 2 \frac{\overset{θ}{\sum_{u = 1}} \min (T_{X_{u}}, T_{Y_{u}})}{\overset{θ}{\sum_{u = 1}} T_{X_{u}} + \overset{θ}{\sum_{u = 1}} T_{Y_{u}}}$ (1)

式(1)中, θ 为样方X和样方Y中共有θ 个物种, $T_{X_{μ}}$ 为样方X中第u个物种的株数, $T_{Y_{μ}}$ 为样方Y中第μ 个物种的株数, min( $T_{X_{μ}}$ , $T_{Y_{μ}}$ )为 $T_{X_{μ}}$ 和 $T_{Y_{μ}}$ 中的较小值。 Bray-Curtis的计算结果越大, 代表样方X和样方Y的共有物种越少, 其beta多样性越高。选取16个调查样方作为训练集, 计算两两之间的beta多样性, 共获得 $\frac{16 \times 15}{2}$ =120组数据。另外9组样方作为验证集, 共有 $\frac{9 \times 8}{2}$ =36组数据。

1.3 无人机高光谱数据采集

由于研究对象为草原植物多样性, 考虑到草本植物植株矮小, 且相似度高, 普通的遥感技术可能难以实现植物多样性的准确估算。因此, 选择了高光谱遥感技术。相比于传统的遥感技术, 高光谱传感器拥有更多的光谱波段, 可以精细地刻画研究对象的细微差异, 传递更多的信息。所以在草原植物多样性监测中可以取得更好的效果。

高光谱数据于无风无云的天气获取, 飞行时间为正午12点。无人机为大疆如风四, 成像光谱仪系统包括光学扫描仪、控制系统和GNSS/IMU组合导航系统(图2)。影像光谱分辨率为5.5 nm, 空间分辨率为0.2 m, 光谱范围为398~1 002 nm, 共有112个波段。为保证数据质量, 仅选择400~900 nm的波段参与以下分析。对影像进行辐射定标、大气校正等预处理, 得到地表反射率数据(图3)。

	Figure Option View Download New Window
	图2 无人机成像光谱仪集成装置(a)与光学扫描仪SPECIM FX10(b)Fig.2 UAV imaging spectrometer integration device (a) and optical scanner SPECIM FX10 (b)

	Figure Option View Download New Window
	图3 高光谱影像(a)以及典型物种、土壤的光谱曲线(b)Fig.3 Hyperspectral image (a) and spectral curves of typical species and soil (b)

1.4 光谱指数构建

由于使用了高光谱遥感技术, 因此每个地物都可以得到一条独特的、连续的光谱曲线[图3(b)], 这使我们可以更好的区分地物之间的差异。相比于普通的遥感技术, 从高光谱遥感的角度使得我们能够使用更多的波段去构建光谱指数并挑选特征波段, 其112个光谱波段为光谱指数的构建提供了丰富的数据支持。

1.4.1 亚尺度观测

当为亚尺度观测时(像元大小< 样方大小), 从光谱距离、光谱角度和生物多样性概念三个方面构建光谱指数。

由于影像空间分辨率为0.2 m, 样方大小为1 m, 故每个样方可覆盖25个像元。计算每个像元的NDVI值, 并根据NDVI的大小将25个像元由小到大排序。由于beta多样性只考虑植物种类和数量的不同, 不考虑植株在空间分布位置的不同, 即群落(A、 B、 C、 D)和群落(B、 D、 A、 C)之间beta多样性为零(A、 B、 C、 D为四种植物)。因此将每个样方的25个像元按NDVI的大小排序, 可减小将物种空间分布不同误认是物种组成不同的概率。基于排序后的数据, 构建了多像元的光谱距离指数和多像元的光谱角度指数。

光谱距离的计算公式为

$Spectral_distance_Mutil = \sqrt[]{\overset{N}{\sum_{j = 1}} \overset{S}{\sum_{i = 1}} (ρ_{X_{i}^{j}} - ρ_{Y_{i}^{j}})^{2}}$ (2)

式(2)中, S为高光谱遥感影像的波段数量, N为样方内覆盖的像元数量, $ρ_{X_{i}^{j}}$ 为样方X中排序后的第j个像元在波段i的反射率, $ρ_{Y_{i}^{j}}$ 为样方Y中排序后的第j个像元在波段i的反射率。该公式计算两个样方的所有像元光谱曲线之间的距离, 距离越大, Spectral_distance_Mutil的值越大, 代表样方对之间的共有种越少, 物种beta多样性越高。

光谱角度的计算公式为

$\begin{array}{l} Spectral_angle_Mutil = \\ \frac{\overset{N}{\sum_{j = 1}} \arccos \{\frac{\overset{S}{\sum_{i = 1}} ρ_{X_{i}^{j}} ρ_{Y_{i}^{j}}}{{[\overset{S}{\sum_{i = 1}} (ρ_{X_{i}^{j}})^{2}]}^{1 / 2} \times {[\overset{S}{\sum_{i = 1}} (ρ_{Y_{i}^{j}})^{2}]}^{1 / 2}}\}}{N} \end{array}$ (3)

式(3)中, S、 N、 $ρ_{X_{i}^{j}}$ 、 $ρ_{Y_{i}^{j}}$ 的含义与式(2)一致。该公式计算两个样方的所有像元光谱曲线之间的角度, 角度越大, Spectral_angle_Mutil的值越大, 物种beta多样性越高。

参考生物多样性概念中的Bray-Curtis指数和Jaccard指数, 以及光谱变异系数CV^[10]的构建形式, 构建了光谱Bray-Curtis指数和光谱Jaccard指数。这两个指数的基本假设是: 不同物种在同一波段的反射率不同, 而相同物种在同一波段的反射率相同。

光谱Bray-Curtis指数的计算公式为

$Spectral_Bray⁃Curtis = \frac{\overset{S}{\sum_{i = 1}} [1 - 2 \frac{\overset{τ}{\sum_{ε = 1}} \min (κ_{X_{i}^{ε}}, κ_{Y_{i}^{ε}})}{\overset{τ}{\sum_{ε = 1}} κ_{X_{i}^{ε}} + \overset{τ}{\sum_{ε = 1}} κ_{^{ε} Y_{i}}}]}{S}$ (4)

式(4)中, τ 为样方X和样方Y中的像元在某波段共有τ 种像元值, $κ_{X_{i}^{ε}}$ 为样方X的像元在第i波段, 第ε 种像元值的像元数量; $κ_{Y_{i}^{ε}}$ 为样方Y的像元在第i波段, 第ε 种像元值的像元数量; min( $κ_{X_{i}^{ε}}$ , $κ_{Y_{i}^{ε}}$ )为 $κ_{X_{i}^{ε}}$ 和 $κ_{Y_{i}^{ε}}$ 的较小值; S为波段数。

光谱Jaccard指数的计算公式为

$Spectral_Jacc ard = \frac{\overset{S}{\sum_{i = 1}} [1 - c_{i} / (a_{i} + b_{i} - c_{i})]}{S}$ (5)

式(5)中, a_i为样方X的像元在波段i的像元值类别数, b_i为样方Y的像元在波段i的像元值类别数, c_i为样方X和样方Y的像元在波段i上像元值相同的类别数, S为波段数。

1.4.2 等尺度观测

当为等尺度观测时(像元大小=样方大小), 从光谱距离和光谱角度两个方面计算光谱指数。首先将影像空间分辨率重采样至1 m大小, 然后提取每个样方所对应的单个像元的光谱曲线, 最后计算光谱曲线之间的距离和角度。

光谱距离的计算公式为

$Spectral_distance_Single = \sqrt[]{\overset{S}{\sum_{i = 1}} (ρ_{X_{i}} - ρ_{Y_{i}})^{2}}$ (6)

式(6)中, S为高光谱遥感影像的波段数量, $ρ_{X_{i}}$ 为样方X所对应的像元在波段i的反射率, $ρ_{Y_{i}}$ 为样方Y所对应的像元在波段i的反射率。 Spectral_distance_Single的值越大, 植物beta多样性越高。

光谱角度的计算公式为

$\begin{array}{l} Spectral_angle_Single = \\ \arccos \{\frac{\overset{S}{\sum_{i = 1}} ρ_{X_{i}} ρ_{Y_{i}}}{{[\overset{S}{\sum_{i = 1}} (ρ_{X_{i}})^{2}]}^{1 / 2} \times {[\overset{S}{\sum_{i = 1}} (ρ_{Y_{i}})^{2}]}^{1 / 2}}\} \end{array}$ (7)

式(7)中, S、 $ρ_{X_{i}}$ 、 $ρ_{Y_{i}}$ 的含义与式(6)一致。 Spectral_angle_Single的值越大, 植物beta多样性越高。

上述6种光谱指数的计算均在R语言中完成。

1.5 重采样

在ENVI中将0.2 m空间分辨率的高光谱影像分别重采样至0.25、 0.33、 0.5和1 m, 重采样后每个样方所对应的光谱曲线数量分别为16、 9、 4、和1(图1)。

1.6 光谱变换

为了提高光谱信息的信噪比, 消除噪声, 对原始光谱数据分别做一阶导数变换和Savitzky-Golay平滑滤波^[11]。光谱变换在MATLAB中完成。

1.7 特征波段选择

选择了三种经典的特征波段提取算法: 相关系数法(correlation analysis, CA)、连续投影算法(successive projections algorithm, SPA)、竞争性自适应重加权算法(competitive adaptive reweighted sampling, CARS)^[12]。 CA在SPSS中完成, SPA和CARS在MATLAB中完成。

1.8 曼特尔检验

植物beta多样性和光谱指数的计算结果均可表示为距离矩阵的形式, 为了验证光谱指数的有效性, 可以检验两个矩阵的相似程度。两个矩阵越相似, 代表该光谱指数的效果越好。曼特尔检验(Mantel test)就是一种验证两个距离矩阵的相关性的统计检验方法, 用于判断一个矩阵中的样本距离与另一矩阵中的样本距离是否相关^{[13, 14]}。 Mantel test在R语言中完成。

2 结果与讨论

2.1 植物多样性地面调查结果

受采矿的影响, 群落组成有较明显的变化, 群落类型包括羊草-糙隐子草、糙隐子草-寸草苔、寸草苔-星毛委陵菜等。计算了16个样方两两之间的Bray-Curtis值, 共获得了120组结果(图4)。其中A— P代表16个样方, 颜色越深代表Bray-Curtis越大, 其beta多样性也就越高。调查结果显示(表1), Bray-Curtis位于0.144~0.793之间, 平均Bray-Curtis为0.470。最大的Bray-Curtis出现在D— P样方组(图4标* 处), 说明样方D和样方P之间的共有种最少。经调查, 样方D有17个物种, 样方P有8个物种, 但是二者之间仅有3种共有物种。最小的Bray-Curtis出现在F— H样方组(图4标* * 处), 为0.144。经调查, 样方F有9个物种, 样方H有14个物种, 但是二者之间有6种共有物种。

	Figure Option View Download New Window
	图4 Bray-Curtis指数的计算结果Fig.4 The calculation result of Bray-Curtis index

表1 Bray-Curtis指数的描述性统计 Table 1 Descriptive statistics of Bray-Curtis index

2.2 最佳光谱指数

采用相关系数和Mantel test比较光谱指数与Bray-Curtis的相关性, 结果如图5所示。可以看到, 当采用亚尺度观测时, 只有Spectral_distance_Mutil、 Spectral_angle_Mutil与Bray-Curtis的相关系数通过了显著性检验, 且Spectral_distance_Mutil与Bray-Curtis的相关系数通过了0.01显著性检验。 Mantel test的结果表明只有Spectral_distance_Mutil与Bray-Curtis的矩阵相似性达到了显著水平。而严格按照生物多样性概念构造的Spectral_Bray-Curtis和Spectral_Jaccard与Bray-Curtis却毫无相关性。分析其原因认为, Spectral_Bray-Curtis和Spectral_Jaccard的基本假设是: 不同物种在同一波段的反射率不同, 相同物种在同一波段的反射率相同。而实际上, 不同的物种在同一波段可能具有相同的反射率。另外, 同物异谱会导致相同物种在同一波段的反射率不同。而光谱距离指数和光谱角度指数的基本假设是: 相同的物种其光谱之间的距离或夹角较小, 不同的物种其光谱之间的距离或夹角较大。显然, 该假设不如Spectral_Bray-Curtis和Spectral_Jaccard的假设那么严格, 相对较宽松, 也就更不容易受偶然误差的影响。当采用等尺度观测时, 不论是相关系数还是Mantel tests均表明, Spectral_distance_Single的效果更好, 光谱距离比光谱角度更适合用于表征植物beta多样性。这是因为不同物种光谱之间的角度不如距离那样明显, 从图5可知, 光谱距离的值域在0~6 100之间, 而光谱角度的值域在0~0.12之间。综上, 不论是采用亚尺度观测还是等尺度观测, 最佳的光谱指数均为光谱距离指数。

	Figure Option View Download New Window
	图5 光谱指数与Bray-Curtis的相关性 * 通过0.05显著性检验; * * 通过0.01显著性检验Fig.5 Correlation between spectral indices and Bray-Curtis * Passed the 0.05 significance test; * * Passed the 0.01 significance test

2.3 最佳影像空间分辨率

将空间分辨率为0.2 m的影像重采样至0.25、 0.33和0.5 m后, 按照式(2)重新计算Spectral_distance_Mutil, 并与Bray-Curtis指数做相关性分析(相关系数和Mantel test), 其结果如图6所示。不同空间分辨率下的光谱距离指数与Bray-Curtis指数的Pearson's r均通过了0.01显著性检验, 且Mantel test的p值也均小于0.05, 达到显著性水平。说明在不同影像空间分辨率下光谱距离指数均可较好的指示植物beta多样性, 具有一定的稳定性, 但是不同空间分辨率下的效果有所差异。

	Figure Option View Download New Window
	图6 不同空间分辨率下光谱距离指数与Bray-Curtis的相关性(括号中的数字为Mantel test的p值)Fig.6 Correlation between spectral distance index and Bray-Curtis at different spatial resolutions (numbers in parentheses are p values of Mantel test)

从空间分辨率为1 m的等尺度观测提高到空间分辨率为0.5 m的亚尺度观测后, 虽然空间分辨率提高了, 但是光谱距离指数的指示能力却有所下降。这是因为当使用多条光谱曲线构建指数时, 指数本身就被引入了群落内多条光谱曲线之间的差异(组内方差), 而我们是想用该指数去指示群落之间的差异(组间方差), 此时光谱距离指数传递的信息不仅有组间差异也自带组内差异, 因此与Bray-Curtis指数的相关性下降。而在等尺度观测时, 由于只用了一条光谱曲线, 故不存在组内方差的问题。同样的, Gholizadeh等^[4]发现提高光谱分辨率后, 使用更多光谱曲线构建的光谱指数可以更好的指示alpha多样性(群落内多样性), 这也是因为更多的光谱曲线带有更多的组内方差信息。而随着空间分辨率的进一步提高, 光谱距离指数与Bray-Curtis指数的相关性也随之提高。这是因为此时可以逐渐观测到物种水平, 可以更清晰的“ 看到” 群落内的物种组成情况, 有助于识别出不同的物种, 进而计算出其光谱距离。但是当分辨率进一步提高后, 光谱距离指数与Bray-Curtis指数的相关性出现了下降。我们认为样方中的非植被地物是降低光谱距离指数估算能力的主要原因。由于影像空间分辨率的提高, 非植被地物(如裸露的土壤、石块)可以被单个像元捕捉到, 而这些像元的光谱曲线与植被光谱曲线相差很大, 从而会被误认为是一种新的“ 物种” , 因此会引入误差。另外, 若某个植被像元的周边有较多非植被像元, 则该植被像元的光谱曲线也会受到这些非植被像元的影响, 从而引入误差。

综上, 光谱距离指数在不同影像空间分辨率下均可较好的指示植物beta多样性。在草甸草原地区, 其最佳的空间分辨率约为0.25 m。需要注意的是, 光谱信号不仅传递了样方内物种组成的信息, 还会受背景因素的影响, 如样方内植被覆盖度和土壤质地。本研究是在草甸草原(植被覆盖度约为70%)、土壤质地为暗栗钙土的条件下完成的。由于研究区环境具有较好的同质性, 因此植被覆盖度和土壤质地的变异对结论影响不大。

2.4 光谱变换的影响

由于用0.25 m空间分辨率的影像计算的光谱距离指数最能反映植物beta多样性, 故在0.25 m空间分辨率的影像上提取光谱曲线, 分别做一阶导数变换和S-G滤波, 用光谱变换后的数据按照式(2)重新计算Spectral_distance_Mutil。从图7可知, 无论是Mantel test还是相关系数均表明: 一阶导数变换显著的提高了Spectral_distance_Mutil与Bray-Curtis 的相关性, 相关系数从0.279提高到0.481, Mantel检验从0.02降低到0.001。而S-G滤波非但没有提高该指数的性能, 反而有所降低。我们认为, 这是因为背景因素(植被覆盖度、土壤等)会对光谱曲线产生影响, 而一阶导数变换可以削弱环境背景值的影响。 S-G滤波可以平滑光谱曲线, 但是光谱的一些特征(吸收谷、反射峰)也有可能因此变得不明显, 从而失去对不同地物的诊断能力。

	Figure Option View Download New Window
	图7 光谱变换后Spectral_distance_Mutil与Bray-Curtis的相关性Fig.7 Correlation between Spectral_distance_Mutil and Bray-Curtis after spectral transformation

2.5 特征波段

由2.4节可知, 对光谱曲线做一阶导数变换可取得最好的效果, 故接下来仅对一阶导数变换后的结果选择特征波段。从图8可知, 采用相关系数法和SPA法选择特征波段后, Spectral_distance_Mutil与Bray-Curtis的相关性增强, 其中相关系数法的效果最为明显, 相关系数达到0.718, Mantel test通过了0.001显著性检验。从图中也可以看出, 采用相关系数法挑选特征波段后得到的光谱距离矩阵图与图4的植被beta多样性距离矩阵图极其相似。说明此时Spectral_distance_Mutil与Bray-Curtis具有极强的相关性。而CARS算法的结果却不尽人意, 相比于全波段运算结果, 其相关系数仅提高了0.007。

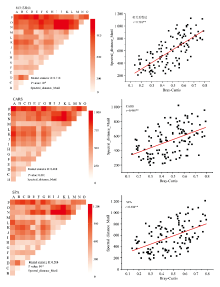	Figure Option View Download New Window
	图8 选择特征波段后Spectral_distance_Mutil与Bray-Curtis的相关性Fig.8 Correlation between Spectral_distance_Mutil and Bray-Curtis after using characteristic bands

图9展示了相关系数法选择的特征波段分布区间, 大部分特征波段位于近红外、红边和绿光, 少部分位于“ 红谷” 。杨芳^[15]对比了植被的光谱反射特征后得出结论: 在近红外波段, 不同植被之间的反射率差异较大, 很适合用来区分植被。周兰萍^[16]同样得出结论: 在近红外波段各植物的反射率差异大, 可用来识别物种。而红边波段则被广泛用于诊断植物胁迫, 对植物生理参数(如叶绿素含量)较为敏感, 同样可用于区分物种^[17]。同时, 不同植物的“ 红谷” 位置和在绿光的反射率也会有所差异。从图3可看出, 本研究区典型物种的光谱曲线在绿光、红边和近红外区间有较大差异。因此这些特征波段可以被用来有效地区分物种, 而beta多样性的实质就是测度物种的多样性。可以看到, 上述这些特征波段大多与植被的生化参数(叶绿素、花青素、类胡萝卜素、氮含量等)有很好的相关性。

	Figure Option View Download New Window
	图9 草原植物beta多样性的特征波段Fig.9 The characteristic bands of plants beta-diversity in grassland

2.6 模型精度验证

用经过一阶导数变换并提取了特征波段的光谱数据按照式(2)计算Spectral_distance_Mutil, 并与Bray-Curtis建立回归模型。模型为Bray-Curtis=0.000 488× Spectral_distance_Mutil+0.184 104, 模型的R²为0.516, 显著性值小于0.000 1, 说明模型具有较好的统计学意义。利用验证集对该模型进行检验(图10), 模型估算值和真实值的相关系数为0.685, R²为0.469, 通过了0.01显著性检验。散点图具有较好的收敛性, 且大致分布在1∶ 1线附近, 说明利用Spectral_distance_Mutil构建的回归模型可以较好的估算植物beta多样性。

	Figure Option View Download New Window
	图10 真实值与估算值的散点图及相关性(n=36)Fig.10 Scatter plot and correlation between true value and estimated value (n=36)

3 结论

基于高光谱遥感技术, 计算了多种草甸草原植物beta多样性估算指数。最佳的指数为光谱距离指数, 该指数在不同尺度下均表现良好, 当影像空间分辨率约为0.25 m时, 该指数效果最佳。对该指数进行光谱变换(一阶导数法)并提取特征波段(相关系数法)后可显著提高其性能。今后可尝试将该方法与已有的植被指数结合, 并应用于其他生态系统类型以验证其普适性。

参考文献

文献列表

[1]	LIN Chen, GONG Ming-hao, LIU Yang, et al(蔺琛, 龚明昊, 刘洋, 等). Acta Ecologica Sinica(生态学报), 2018, 38(13): 4677. [本文引用:1]
[2]	TIAN Jia-yu, WANG Bin, ZHANG Zhi-ming, et al(田佳玉, 王彬, 张志明, 等). Chinese Journal of Plant Ecology(植物生态学报), 2022, 46(10): 1129. [本文引用:1]
[3]	YANG Xing-chen, LEI Shao-gang, XU Jun, et al(杨星晨, 雷少刚, 徐军, 等). Journal of Arid Land Resources and Environment(干旱区资源与环境), 2022, 36(6): 105. [本文引用:1]
[4]	Gholizadeh H, Gamon J A, Townsend P A, et al. Remote Sensing of Environment, 2019, 221: 38. [本文引用:3]
[5]	FU Han-pei, WANG Rang-hu, WANG Xiao-jun(付含培, 王让虎, 王晓军). Research of Soil and Water Conservation(水土保持研究), 2022, 29(2): 145. [本文引用:1]
[6]	Cui L, Zhao Y, Liu J, et al. ISPRS International Journal of Geo-Information, 2021, 10(10): doi: DOI:10.3390/ijgi10100679. [本文引用:1]
[7]	Wang R, Gamon J A, Cavender-Bares J, et al. Ecological Applications, 2018, 28(2): 541. [本文引用:2]
[8]	Onyia N N, Balzter H, Berrio J C, Remote Sensing, 2019, 11(22): 2662. (doi: DOI:10.3390/rs11222662). [本文引用:1]
[9]	PENG Yu, TAO Zi-ye, XU Zi-yan, et al(彭羽, 陶子叶, 许子妍, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(7): 2016. [本文引用:1]
[10]	Gholizadeh H, Gamon J A, Zygielbaum A I, et al. Remote Sensing of Environment, 2018, 206: 240. [本文引用:1]
[11]	QIAN Yu-rong, YU Jiong, JIA Zhen-hong, et al(钱育蓉, 于炯, 贾振红, 等). Acta Prataculturae Sinica(草业学报), 2013, 22(1): 157. [本文引用:1]
[12]	FENG Zi-heng, LI Xiao, DUAN Jian-zhao, et al(冯子恒, 李晓, 段剑钊, 等). Acta Agronomica Sinica(作物学报), 2022, 48(9): 2300. [本文引用:1]
[13]	Hoffmann S, Schmitt T M, Chiarucci A, et al. Applied Vegetation Science, 2019, 22(1): 13. [本文引用:1]
[14]	Chaves P P, Echeverri N R, Ruokolainen K, et al. Journal of Vegetation Science, 2021, 321: e12938. (doi: DOI:10.1111/jvs.12938). [本文引用:1]
[15]	YANG Fang, CHEN Dong-hua, LI Hu, et al(杨芳, 陈冬花, 李虎, 等). Remote Sensing Information(遥感信息), 2016, 31(3): 88. [本文引用:1]
[16]	ZHOU Lan-ping, WEI Huai-dong, DING Feng, et al(周兰萍, 魏怀东, 丁峰, 等). Journal of Arid Land Resources and Environment(干旱区资源与环境), 2013, 27(3): 121. [本文引用:1]
[17]	LIU Yong-mei, GAI Xing-hua, DONG Xing-zhi, et al(刘咏梅, 盖星华, 董幸枝, 等). Journal of Northwest University (Natural Science Edition) [西北大学学报(自然科学版)], 2022, 52(2): 159. [本文引用:1]

2018

0.0

... 引言生物多样性是生态系统的主导功能, 是水源涵养、土壤保持、气候调节等功能得以实现的基础^[1] ...

2022

0.0

... 目前, 光谱技术被广泛用于植物多样性的快速估算^[2] ...

2022

0.0

... 不论是直接法^[3]还是间接法^[4], 都有许多成功的案例 ...

2019

0.0

... 不论是直接法^[3]还是间接法^[4], 都有许多成功的案例 ...

... Wang^[7]等认为估算草原植物多样性时像元空间分辨率不应低于10 cm, 而Gholizadeh等^[4]同样以草原为研究对象, 发现影像空间分辨率为1 m时, 光谱指数与alpha多样性仍具有很好的相关性 ...

... 同样的, Gholizadeh等^[4]发现提高光谱分辨率后, 使用更多光谱曲线构建的光谱指数可以更好的指示alpha多样性(群落内多样性), 这也是因为更多的光谱曲线带有更多的组内方差信息 ...

2022

0.0

... 例如, 经典的NDVI(normalized difference vegetation index)指数被认为与植被覆盖度具有很强的相关性, 并被广泛用于直接表征植被覆盖度^[5]或构建植被覆盖度估算模型^[6] ...

2021

0.0

2018

0.0

... 对于alpha多样性, 光谱变异系数被认为与群落内物种丰富度具有强相关性, 大量研究用光谱变异系数的大小来表示alpha多样性的高低^[7,8] ...

2019

0.0

... 对于alpha多样性, 光谱变异系数被认为与群落内物种丰富度具有强相关性, 大量研究用光谱变异系数的大小来表示alpha多样性的高低^[7,8] ...

2020

0.0

... 彭羽等^[9]利用手持式地物光谱仪研究了如何估算植物物种beta多样性, 并构建了一些较好的指数 ...

2018

0.0

... 参考生物多样性概念中的Bray-Curtis指数和Jaccard指数, 以及光谱变异系数CV^[10]的构建形式, 构建了光谱Bray-Curtis指数和光谱Jaccard指数 ...

2013

0.0

... 6 光谱变换为了提高光谱信息的信噪比, 消除噪声, 对原始光谱数据分别做一阶导数变换和Savitzky-Golay平滑滤波^[11] ...

2022

0.0

... 7 特征波段选择选择了三种经典的特征波段提取算法: 相关系数法(correlation analysis, CA)、连续投影算法(successive projections algorithm, SPA)、竞争性自适应重加权算法(competitive adaptive reweighted sampling, CARS)^[12] ...

2019

0.0

... 曼特尔检验(Mantel test)就是一种验证两个距离矩阵的相关性的统计检验方法, 用于判断一个矩阵中的样本距离与另一矩阵中的样本距离是否相关^[13,14] ...

2021

0.0

2016

0.0

... 杨芳^[15]对比了植被的光谱反射特征后得出结论: 在近红外波段, 不同植被之间的反射率差异较大, 很适合用来区分植被 ...

2013

0.0

... 周兰萍^[16]同样得出结论: 在近红外波段各植物的反射率差异大, 可用来识别物种 ...

2022

0.0

... 而红边波段则被广泛用于诊断植物胁迫, 对植物生理参数(如叶绿素含量)较为敏感, 同样可用于区分物种^[17] ...