研究区为河北省涞源县铅锌矿区, 区域内金属矿产较为丰富, 主要以铅、 锌为主。 该区域位于涞源县城东北方向约30 km处, 研究区面积约 4.3 km², 其中心地理坐标为: 东经 114° 55'16″, 北纬 39° 22'24″。 区域海拔高度600~1 032.89 m, 相对高差约432 m。 采矿区土壤的主要类型是棕壤土和褐土, 土壤受到重金属污染、 大多属于酸性土壤, 存在盐碱化, 从土壤质地来看, 以砾石和物理性砂粒为主, 土质通气性较好。 土壤中的重金属易迁移到斜坡和谷地中。 而采矿作业过程中所产生的尾矿、 废水、 废矿石等废弃物未得到及时有效的处理, 会使矿区周围土壤重金属含量增加, 同时影响植被的生长和居民健康。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区地理位置及采样点位置图Fig.1 Geographical location of the study area and location of sampling points

实验样本来自河北省涞源县铅锌矿区, 共收集100个土壤样品。 根据现场实际位置及地理特点, 沿着两条研究区的沟谷, 布设条带状取样带采集土壤样本。 将样品研磨成100个粉末样品, 每个样品分为两部分, 分别用于化学分析和光谱实验。 使用美国SVC公司生产的SVC HR-1024i地物光谱仪(350~2 500 nm)获取土样品的光谱数据。 在实验室内利用电感耦合等离子体质谱法测定土壤中的镉、 铅和锌的含量。 地物光谱仪(SVC HR-1024i)光谱覆盖可见光-近红外波段, 光谱仪三个光电二极管对应三个衍射光栅分光计, 分别为1个硅(Si)(350~1 000 nm)和2个砷化钠(InGaAs)(1 000~1 850 nm和1 850~2 500 nm)的二极管阵列。 其中硅阵列(350~1 000 nm)有512个离散探测器, 砷化钠阵列(1 000~2 500 nm)各有256个离散探测器, 能够获取1 024个波段的光谱数据。 在实验室内对土壤样本进行光谱测量。 打开卤素灯源。 将光纤探头固定于铁架台上, 控制与样本之间的距离。 100个标样各测量2次, 取平均值作为最终土样本光谱。

由于土壤样本采集制备及化验测试过程中人为或系统误差的影响会出现异常值, 使用箱型图法对获取的研究区重金属数据进行异常值剔除。

箱型图法是一种比较常用的重金属含量异常值识别方法^[14], 该方法的基本原理: 利用Box-plot工具对重金属含量异常值进行检测, 发现三种重金属元素化学测试结果存在不同程度的极端异常值和温和异常值, 利用箱型图的截距线Q3+1.5× IQR和Q1+1.5× IQR(其中Q3为上四分位数, Q1为下四分位数, IQR 为四分位数的间距)作为阈值范围对土壤重金属含量数据的极端异常值进行剔除。

样本在进行光谱数据采集时容易受到仪器和环境变化的影响。 获得的光谱包括噪声光谱数据和地物光谱数据。 通过光谱数据预处理和各种变换, 可以有效地降低噪声, 有利于土壤光谱数据的特征提取, 提高反演建模精度。

2.1.1 Savitzky-Golay平滑法

Savitzky-Golay(SG)平滑算法是一种基本的平滑方法, 信号平滑处理可以除去高频噪声对数据信号的干扰, 是消除噪音最常用的一种方法。 相比于传统去除噪声的算法, 该算法更稳定、 误差更小, 同时不受样本数据的限制。 计算公式如式(1)所示

Xi* =∑-rrXi+jWj∑j=-rrWj(1)

式(1)中, Xi*是平滑后的数据, W_j是移动窗口平滑中的加权因子。 该值是多项式的拟合系数, 窗口长度为2r+1。

2.1.2 光谱导数

光谱导数处理有助于减少低频噪声对目标光谱的影响^[15], 一阶光谱导数可以显著增强光谱的细节变化信息, 减弱大气效应、 背景噪声对采集光谱的干扰, 同时能够反映研究对象的一些生物、 化学成分信息, 在植被、 土壤、 矿物等领域中有着广泛的应用^[16]。 FD计算方法如式(2)

R'i=Ri-Ri-1ωi-ωi-1(2)

式(2)中, R_i为第i个波段光谱的反射率, ω _i为第i个波段的波长

2.1.3 多元散射校正

MSC是常用的一种数据处理方法, 经过散射校正后得到的光谱数据可以增强与成分含量相关的光谱吸收信息。 MSC计算的具体过程如下:

计算待校正光谱的平均光谱

A̅=∑i=1nAin(3)

建立基于基准数据的一元线性回归, 确定每一个样本的回归系数及偏置

Ai=miA̅+bi(4)

对原始样本进行校正处理

Ai(msc)=Ai-bimi(5)

式中, A_i为校准光谱数据矩阵; A̅i, j是样品通过SG算法平滑后, 通过平均每个波长的近红外光谱获得的平均光谱矢量; m_i和b_i分别是与平均光谱进行一元线性回归后获得的相对偏移系数和平移量^[17]。

2.1.4 标准正态变换

SNV可去除光谱乘性噪声^[18], 其实质是使原始光谱数据标准正态化, 计算方法如式(6)

Ri* =Ri-R̅σR(6)

式(6)中, R_i为第i个波段光谱的反射率, R̅为一个样本光谱反射率的均值, σ R为一个样本光谱反射率的标准差。

2.1.5 光谱指数构建

为了提高重金属含量反演的准确性, 构建了三个光谱指数: DI、 RI和NDI^[19]。 利用建立的指标分析了样品的光谱特征与重金属含量之间的相关性。 各指标的计算方法如式(7)— 式(9)

RI=RλmRλn(7)

DI=Rλm-Rλn(8)

NDI=Rλm-RλnRλm+Rλn(9)

式中, λ m是对应于点m的波长位置; λ n是对应于点n的波长位置; R_{λ m}是波长λ m对应的反射率值, R_{λ n}是波长λ n对应的反射率值。

2.2.1 随机森林算法

RF通过自重法重采样技术, 随机抽取样本和特征, 建立多棵相互不关联的决策树, 通过并行的方式获得预测结果^[20]。 每棵决策树都能通过抽取的样本和特征得出一个预测结果, 综合所有树的结果取平均值, 得到整个森林的回归预测结果。

2.2.2 偏最小二乘回归算法

PLSR是一种常用的非线性回归模型。 与早期的最小二乘回归模型相比, 可以得到偏最小二乘算法和综合变量。 基于综合变量模型, 样本空间太小, 输入和输出变量之间存在高度相关性^[21]。 偏最小二乘算法模型分别从输入变量和输出变量中提取主成分t₁和u₁, 其中t₁是输入变量的线性组合, u₁是输出变量的线性拟合。 算法必须满足以下要求:

(1)t₁和u₁是变量和输出变量的最大变化信息;

(2)t₁和u₁之间的相关性最大;

提取主成分时, PLSR模型的输入变量X将对t₁进行回归分析, 而输出变量Y将对u₁进行回归分析。 模型是否会继续提取主成分的标准是模型的测试精度。 如果精度满足要求, 则主成分的提取将停止。 否则, 重复这些步骤提取主成分, 直到模型精度满足要求^[22]。

2.2.3 精度评价方法

利用R²、 RMSE、 MAE对模型的精度进行综合评价^[23]。 R²用来表征回归线与观测值的拟合程度, 其值在0和1之间。 R²越高, 模型拟合效果越好。 即光谱指数模型对重金属含量解释得越好, 参考值越大。 RMSE反映了样本离散程度, 可用于观察重金属含量真实值与预测值之间的偏差。 MAE是绝对误差的平均值, 可以更好地反映预测值误差的实际情况, R²越大, RMSE、 MAE越小为最优模型。 计算方式如式(10)— 式(12)

R2=1-∑i=1n(yi-y^i)2∑i=1n(yi-y̅i)2(10)

RMSE=1n∑i=1(yi-y^i)2(11)

MAE=1n∑i=1n|yi-y^i|(12)

式中, y_i为要拟合的值, 其平均值为 y̅i, 拟合值为 y^i, n为实验次数。

土壤样品中重金属含量的描述性统计(表1)。

表1

Table 1

表1(Table 1)

表1 土壤中重金属含量描述性统计 Table 1 Descriptive statistics of heavy metal content in soil 最大值/ (mg· kg-1) 最小值/ (mg· kg-1) 平均值/ (mg· kg-1) 标准差 变异系数 /% 河北省土壤背景值/ (mg· kg-1) Cd 6.07 0.12 1.03 1.32 128 0.075 Pb 473.60 13.35 104.49 110.78 106 20 Zn 644.22 66.65 183.49 127.72 70 62

表1 土壤中重金属含量描述性统计 Table 1 Descriptive statistics of heavy metal content in soil

表1为土壤重金属Cd、 Pb、 Zn含量测定结果, 其中土壤背景值是参照《土壤环境质量农用地土壤污染风险管控标准》(GB 15618— 2018)中pH> 7.5对应数值。 研究区内土壤重金属Cd、 Pb、 Zn元素平均值分别为1.03、 104.49和183.49 mg· kg^-1, 分别超过河北省土壤环境背景值13.73、 5.22和2.96倍, 表明矿区土壤重金属存在明显积累, 尤其是Cd元素。 变异系数可以反映样本受人为影响的程度和样本在所有样本中的平均变异程度, 有研究认为变异系数≤ 10%为弱变异, 10%~100%为中等变异, ≥ 100%为高度变异。 由表1可知, Cd、 Pb元素属于高度变异, 说明Cd、 Pb元素空间分异大, 其空间分布受外界干扰显著, Zn元素属于中等变异, 变异程度由大到小依次为Cd> Pb> Zn。

图2绘制了100个土壤样品的可见-近红外光谱反射曲线。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 土壤光谱反射曲线Fig.2 Soil reflectance spectral curves

光谱曲线大致相似, 光谱反射率为3%~50%; 在约1 950和2 200 nm波段的吸水特性更为明显, 并表现出一定的吸收谷。 在约400~650 nm范围内, 光谱反射率较低, 反射率随波长的增加而迅速增加。 在650~1 400 nm范围内, 反射率随波长的增加而增加, 但振幅的增加有所减小。 在2 100 nm处, 反射率开始降低。

利用箱型图法(图3)对土壤样本重金属含量进行异常值剔除的结果(表2)。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 异常值剔除后箱型图Fig.3 Box plots after removing outliers

表2

Table 2

表2(Table 2)

表2 重金属含量异常值剔除 Table 2 Removal of abnormal values of heavy metal content 剔除前样本/个 剔除后样本/个 Cd 100 89 Pb 100 90 Zn 100 70

表2 重金属含量异常值剔除 Table 2 Removal of abnormal values of heavy metal content

表2可以看出, Cd、 Pb和Zn这三种重金属土壤样本化学测试结果存在一定程度的异常值, 其中在Zn元素异常值最多, 可能是在采矿运输过程中造成的局部异常。 基于剔除异常土壤样本后的数据集开展后续研究。

利用六种光谱预处理方法处理的数据构建了三个光谱指数(RI、 DI和NDI), 并分析了重金属含量与光谱指数之间的相关系数。 图4(a)— (f)展示了镉含量与原始光谱数据DI、 多元散射校正后DI、 标准正态变换后DI、 一阶导数后DI、 多元散射校正和一阶导数后DI以及标准正态变换和一阶导数后DI的相关分布。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 镉含量与差值指数的相关分布图 (a): 原始光谱; (b): MSC; (c): SNV; (d): FD; (e): MSC+FD; (f): SNV+FDFig.4 Correlation distribution between cadmium contents and difference indices (a): Original spectra; (b): MSC; (c): SNV; (d): FD; (e): MSC+FD; (f): SNV+FD

图4中的水平和垂直坐标是样品的光谱波长。 图中的颜色表示光谱差值指数DI与该点样品镉含量之间相关系数的绝对值。 颜色从蓝色逐渐增加到红色, 这表明两个量之间的相关系数的绝对值从0增加到1。 深红色对应着光谱指数和重金属含量之间更强的相关性。 在图4中, 对于镉元素, 原始光谱、 经多元散射校正和标准正态变换后的光谱指数与镉含量相关系数小于0.5, 但经过一阶导数处理后的光谱数据与镉含量的相关性增大, 比原始光谱数据相关系数高。

图5(a)— (f)显示了铅含量与原始光谱数据RI、 多元散射校正后RI、 标准正态变换后RI、 一阶导数后RI、 多元散射校正和一阶导数后RI以及标准正态变换和一阶导数后RI的相关分布。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 铅含量与的比值指数的相关分布 (a): 原始光谱; (b): MSC; (c): SNV; (d): FD; (e): MSC+FD; (f): SNV+FDFig.5 Correlation distribution between lead contents and ratio indices (a): Original spectra; (b): MSC; (c): SNV; (d): FD; (e): MSC+FD; (f): SNV+FD

图5中的颜色表示光谱比值指数RI与该点样品铅含量之间相关系数的绝对值。 如图5, 经过一阶导数处理后的光谱数据与重金属含量的相关性略增大, 比原始光谱数据效果强, 相关系数在0.5左右。

锌含量与原始光谱数据NDI、 多元散射校正后NDI、 标准正态变换后NDI、 一阶导数后NDI、 多元散射校正和一阶导数后NDI以及标准正态变换和一阶导数后NDI的相关分布分别在图6(a)— (f)。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 锌含量与归一化指数的相关分布 (a): 原始光谱; (b): MSC; (c): SNV; (d): FD; (e): MSC+FD; (f): SNV+FDFig.6 Correlation distribution between zinc contents and normalization indices (a): Original spectra; (b): MSC; (c): SNV; (d): FD; (e): MSC+FD; (f): SNV+FD

图6中的颜色表示NDI与该点样品锌含量之间相关系数的绝对值。 经过一阶导数处理后的光谱数据与重金属含量的相关性增大, 比原始光谱数据效果强。 总体来看, 归一化指数与样品重金属含量的相关性低于差值指数和比值指数, 最大相关系数不超过0.5。

表3为对于不同重金属而言, 不同光谱指数下相关性最强的敏感性波段及对应的光谱变换形式。 Cd含量与光谱指数的相关性最高的是2 295和2 168.7 nm, 这是由SNV+FD预处理后光谱数据的DI形成的, Pb含量与光谱指数的相关性最高的是389.9和2 350.8 nm, 这是由FD预处理后光谱数据的DI形成的, Zn含量与光谱指数的相关性最高的是800.3和2 133.3 nm, 这是由MSC+FD预处理后光谱数据的RI形成的。 由表3可知, 重金属光谱数据与重金属含量的相关性最大可达0.57, 最小为0.45, 可以较好的建模与反演。

表3

Table 3

表3(Table 3)

表3 不同光谱指数的重金属敏感波段和相关系数 Table 3 Heavy metal sensitive bands and correlation coefficients of different spectral indices 光谱指数 光谱变换 敏感波段/nm 相关性 DI SNV+FD 2 168.7、 2 295.1 0.570 194 Cd RI SG 2 323.2、 2 327.8 0.469 1 NDI MSC+FD 2 273.8、 2 330.1 0.544 176 DI FD 389.9、 2 350.8 0.553 771 Pb RI FD 2 052.9、 2 168.7 0.514 576 NDI FD 2 052.9、 2 168.7 0.545 708 DI MSC 2 173.7、 2 178.7 0.450 027 Zn RI MSC+FD 800.3、 2 133.3 0.490 949 NDI FD 794、 2 158.7 0.484 951

表3 不同光谱指数的重金属敏感波段和相关系数 Table 3 Heavy metal sensitive bands and correlation coefficients of different spectral indices

通过分析可知, 相较于原始光谱, 变换后的光谱对于重金属信息的表达能力显著增强, 光谱变换可以有效提升重金属含量与光谱的相关性, 对于模型效果具有一定提升作用。 各种数据处理方法增强了一些光谱特征, 以光谱数据与重金属含量相关性最大为原则选择表3的数据集作为输入数据, 利用偏最小二乘回归算法和随机森林算法建立重金属含量反演模型。 图7— 图9分别为Cd、 Pb和Zn含量的预测值和真实值的比较结果。

图7

Fig.7

	Figure Option ViewDownloadNew Window
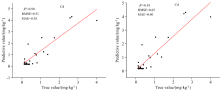	图7 不同算法预测Cd含量与实测Cd含量比较 (a): PLSR; (b): RFFig.7 Comparison of Cd contents predicted by different algorithms and measured Cd content (a): PLSR; (b): RF

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同算法预测Pb含量与实测Pb含量比较 (a): PLSR; (b): RFFig.8 Comparison of predicted Pb contents with different algorithms and measured Pb content (a): PLSR; (b): RF

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 不同算法预测Zn含量与实测Zn含量比较 (a): PLSR; (b): RFFig.9 Comparison of predicted Zn contents with different algorithms and measured Zn content (a): PLSR; (b): RF

表4为利用偏最小二乘回归算法以及随机森林算法对验证集的数据中Cd、 Pb和Zn元素的反演评价指标R²、 RMSE、 MAE的结果。 除Cd外, Pb和Zn的随机森林算法反演重金属含量的评价指标优于偏最小二乘回归算法。 这是因为随机森林具有对数据集适应性强、 抗干扰性能好、 拟合能力强的优点, 并且该算法在训练过程中可以根据重金属含量分布自动从样本特征集中提取样本特征的最优组合, 提高了模型的鲁棒性。

表4

Table 4

表4(Table 4)

表4 镉、 铅、 锌反演精度评价对比 Table 4 Comparisons of inversion accuracy evaluation of Cd, Pb, and Zn 模型 R2 RMSE MAE Cd PLSR 0.90 0.51 0.38 RF 0.81 0.65 0.40 Pb PLSR 0.89 42.04 33.91 RF 0.91 40.45 32.56 Zn PLSR 0.81 71.09 48.71 RF 0.84 65.31 39.13

表4 镉、 铅、 锌反演精度评价对比 Table 4 Comparisons of inversion accuracy evaluation of Cd, Pb, and Zn