区间值直觉模糊麦克劳林聚合算子的近红外反射波段划分方法

引用本文

任维佳, 杜向军, 杜玉琴, 孙荣禄, 李学良. 区间值直觉模糊麦克劳林聚合算子的近红外反射波段划分方法[J]. 光谱学与光谱分析, 2024,44(6): 1731-1739.
REN Wei-jia, DU Xiang-jun, DU Yu-qin, SUN Rong-lu, LI Xue-liang. Near Infrared Reflection Band Division Method Based on Interval-Valued Intuitionistic Fuzzy Maclaurin Symmetric Mean Aggregation Operator[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1731-1739.
Doi:10.3964/j.issn.1000-0593(2024)06-1731-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

区间值直觉模糊麦克劳林聚合算子的近红外反射波段划分方法

任维佳^1,^2,³, 杜向军^1,³, 杜玉琴^4,^*, 孙荣禄^1,³, 李学良^1,³

1. 天津工业大学机械工程学院, 天津 300387

2. 天津科技大学机械工程学院, 天津 300222

3. 天津市现代机电装备技术重点实验室, 天津 300387

4. 中国社会科学院大学经济学院, 北京 102401

*通讯作者 e-mail: duyugin@ucass.edu.cn

作者简介: 任维佳, 1993年生, 天津工业大学机械工程学院博士研究生 e-mail: rwj_2020@163.com;
杜向军, 1980年生, 天津工业大学机械工程学院博士研究生 e-mail: dxjun216@163.com;任维佳, 杜向军: 并列第一作者

收稿日期: 2021-11-25 修回日期: 2023-11-02

基金: 国家自然科学基金青年科学基金项目(51205288), 天津市自然科学基金项目(17JCYBJC19400), 天津市研究生科研创新项目(2022BKY140)资助

摘要

采用不同波段光谱对不同类异性纤维进行识别, 可有效剔除异性纤维, 提高检出率。针对波段传统划分方法存在的评价指标单一性问题, 研究不同异性纤维多种属性间相互影响, 结合多属性群决策(MAGDM)方法的优势, 提出利用多属性群决策方法实现棉花中异性纤维最佳检测波段的选取, 根据不同异性纤维多种属性指标的关联性, 综合考虑多种属性指标, 确定波间可分度、相关性和ABS指标作为异性纤维属性的评价指标。首先, 针对多属性群决策方法中评价准则不准确问题, 构建评价准则函数线性方程组, 使其增广矩阵的秩等于未知量个数, 保证方程组具有唯一解, 从而提高决策结果的准确性。接着, 使用幂等(PA)算子消除不合理评价信息数据值对决策结果的负面影响, 结合麦克劳林对称平均(MSM)算子综合考量多个数据间的相互关系, 推导加权区间直觉模糊幂等麦克劳林对称平均(WIVIFPMSM)聚合算子, 拓展TOPSIS方法确定异性纤维权重信息, 聚合不同异性纤维多种属性的评价信息, 根据所建立的评价准则确定决策结果, 进而构建基于区间值直觉模糊集(IVIFS)的多属性决策方法, 实现多种异性纤维多种属性指标的最佳波段选取。将区间值直觉模糊幂等麦克劳林聚合算子与类间可分性波段选择(ISBC)方法和自适应选择(ABS)方法进行了对比, 分析了不同波段划分方法对结果的影响, 总结了现有研究中存在的问题和不足。为提高多属性群决策方法的决策精度, 分析了参数 k对决策结果的影响, 证明区间值直觉模糊幂等麦克劳林聚合方法稳定性更好, 为复杂环境下异性纤维波段划分研究提供了新思路。最后, 通过实验验证近红外波段 W₃: 780~1 100 nm为最佳检测波段。该方法对波段选取领域的理论扩展和多属性群决策方法的应用具有一定的指导意义。

关键词: 异性纤维; 反射率光谱; WIVIFPMSM聚合算子; 多属性决策; 波段选择

中图分类号:TP391.41 文献标志码:A

Near Infrared Reflection Band Division Method Based on Interval-Valued Intuitionistic Fuzzy Maclaurin Symmetric Mean Aggregation Operator

REN Wei-jia^1,^2,³, DU Xiang-jun^1,³, DU Yu-qin^4,^*, SUN Rong-lu^1,³, LI Xue-liang^1,³

1. School of Mechanical Engineering, Tiangong University, Tianjin 300387, China

2. College of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300222, China

3. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology, Tiangong University, Tianjin 300387, China

4. School of Economics, University of Chinese Academy of Social Sciences, Beijing 102401, China

*Corresponding author

REN Wei-jia and DU Xiang-jun: joint first authors

Abstract

Using different wavelength spectra to identify different types of foreign fibers can effectively eliminate foreign fibers and increase the detection rate. Given the problem of a single evaluation index existing in traditional band division methods, the interaction of attribute indexes of different fibers is studied, combined with the advantages of the multi-attribute group decision-making (MAGDM) method, this paper proposes to use the MAGDM method to realize the selection of the optimal detection band for foreign fibers in cotton. According to the relation of attribute indexes of different fibers, the inter-class separability, correlation and ABS index are determined as attribute evaluation indexes. Firstly, to solve the problem of inaccurate evaluation criteria in the MAGDM method, a system of evaluation criteria function linear equations is constructed so that the rank of the augmented matrix is equal to the number of unknowns, ensuring that the equation system has a unique solution, thereby improving the accuracy of the decision result. Next, the power mean (PA) operator is used to eliminate the adverse effects of unreasonable evaluation information values on decision results, combined with the Maclaurin symmetric mean (MSM) operator to comprehensively consider the relationship between input arguments, deriving the weighted interval-valued intuitionistic fuzzy power Maclaurin symmetric mean (WIVIFPMSM) aggregation operator.Then, the TOPSIS method is used to determine the weight information of foreign fibers, the evaluation information of various attributes of different foreign fibers is aggregated, and the decision results are chosenaccording to the established evaluation criteria. Thus, a MAGDM method based on interval-valued intuitionistic fuzzy sets (IVIFSs) is constructed to realize the optimal band selection of various attributes of foreign fibers. Moreover, the WIVIFPMSM aggregation operator is compared with the inter-class separability band selection (ISBC) method and adaptive band selection (ABS) method, the influence of different band division methods on the results are analyzed, and the existing problems and deficiencies in existing research are summarised. To improve the decision accuracy of the MAGDM method, parameter ks influence on decision results is analysed, and it is proved that the IVIFPMSM aggregation method has better stability, which provides a new idea for the study of band division of foreign fibers in complex environments. Finally, it is verified through experiments that the near-infrared band W₃: 780~1 100 nm is the optimal detection band. In addition, this paper has a specificguiding significance for the theoretical extension of band selection and the application of MAGDM methods.

Keyword: Foreign fiber; Reflectance spectrum; WIVIFPMSM operator; Multi-attribute decision making; Band selection

文章图片

引言

“ 十四五” 规划的棉花行业战略方向研究建设报告中要求, 棉花质量检测要进一步加强。棉花中的异性纤维(简称异纤)不仅会造成纱线的断裂, 更影响织物的质量, 造成纺织企业巨大经济损失^[1]。异性纤维是指棉花中混入的非棉纤维和非本色棉纤维等有害物质。目前主要采用图像处理的方法^{[2, 3]}实现棉花中异纤的检测, 利用特定光源照射棉花, 通过将CCD采集到的图像进行数据处理, 找出与棉纤维的差异识别异纤。异性纤维种类繁多, 主要有羽毛、塑料薄膜、化学纤维、丙纶丝。采用不同波段的光源对异纤检测识别精度和分类效果具有显著差别。

波段选择是通过研究波段间的相对距离、可分度和相关性, 划分出可分性大、冗余小的最佳波段; 常用方法为类间可分性和信息量划分方法。类间可分性波段选择是通过分析波段间相对距离研究其可分度。 Bao等^[4]分析单因素方差和Jeffries-Matusita(J-M)距离光谱一致性检验, 并利用J-M距离选取最佳波段; Charifi等^[5]利用Bhattacharyya距离进行可分性检验, 根据可分度选择波段组合; 杨文柱等^[6]利用波段间的类间可分性, 认定780~1 800 nm的近红外波段为最佳检测波段。郏东耀^[7]采用基于区域信息相关度权值小波分析算法将多个波段的信息进行融合, 提出了一种利用多波段光谱信息融合成像检测的新方法。信息量波段选择方法分析波段相关性, 去除波间冗余量, 搜寻信息量最大和相关性最小的波段。 Jiang等^[8]采用最小冗余最大相关性(mRMR)算法选择最优波长, 提高棉花中异纤的分类效果; Wang等^[9]提出了一种基于自适应子空间划分策略(ASPS)波段选择方法; 杨赛等^[10]发现平均光谱和熵联合的分类精度高于单一特征模型, 为波段融合方法提供了理论基础; 马梦茹等^[11]利用OIF和ABS方法进行最佳波段选取, ABS比OIF方法提升精度9.21%。

类间可分性和信息量划分方法均未考虑综合划分指标, 当一种指标达到最优时其他指标无法达到最佳效果, 影响了最终结果。本工作引入多属性决策法, 利用MSM算子^[12]综合考量多个输入参数交互关系, 使用PA算子^[13]削弱极端输入参数的优势, 提出WIVIFPMSM聚合算子^{[14, 15, 16]}, 结合TOPSIS确定各类异性纤维权重向量^[17], 构建最佳波段的多属性决策框架, 实现最佳波段的选取。并将所提方法与类间可分性波段选择(ISBC)和自适应选择(ABS)算法的实验结果进行对比, 验证该方法的合理性和有效性。

1 实验部分

1.1 仪器与样本

实验设备为日立UH4150紫外-可见近红外分光光度计, 可以实现异纤的全光谱检测, 选用的光谱检测范围为240~2 600 nm, 采样间隔为2 nm, 配套软件是UV Solutions 4.2, 参比和样品放置处都要放置Al₂O₃白板, 异纤使用基地和夹片夹持。另外, 处理器采用Intel(R)i7-7400CPU@3.00GH, RAM大小为16 GB。实验样本来源于湖北谷城银纺公司等全国10个棉纺企业实际生产中剔除的异纤, 经初步检查有布块、树叶、白纸、羊毛、羽毛、白色泡沫、麻绳、黑色塑料薄膜、头发、白色塑料薄膜、丙纶丝、化学纤维等多种异纤, 而羽毛、塑料薄膜、化学纤维、丙纶丝含量较多, 作为主要研究对象^[17]。

1.2 数据采集

波段选择方法一般用一组测量数据测验, 缺乏全面性。针对12类异纤进行光谱数据采集, 每类异纤采集10组数据信息, 数据采集过程中按颜色、厚度、疏密度对样本进行调整^[8]。研究光谱信息的变化趋势, 分析数据的可靠性、稳定性, 构造一组合理的综合异纤光谱数据, 以确保波段选择的合理性和科学性。

1.3 波段划分方法

1.3.1 基于类间可分性波段选择算法

为实现波段划分, 研究各类异纤到棉花之间的距离, 采用欧式平均距离进行数据计算。基于波段间距离, 结合各类异纤的可分度, 实现波段划分。平均欧式距离公式为

$dis (V, V') = \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} (v_{i} - v'_{i})^{2}}$ (1)

式(1)中, v_i和v'_i表示目标光谱信息, dis(V, V')表示目标间距离。

根据异纤光谱信息的分布及波动情况, 定义光谱反射率的均值 $f_{i}^{k}$ 和样本标准差 $S_{i}^{k}$ 。

$f_{i}^{k} = \frac{1}{n} \overset{n}{\sum_{i = 1}} R_{i}^{k} (λ)$ (2)

$S_{i}^{k} = \sqrt[]{\frac{1}{n - 1} \overset{n}{\sum_{i = 1}} [R_{i}^{k} (λ) - f_{i}^{k}]^{2}}$ (3)

建立第i种与第j种异纤反射光谱可区分度, 模型为

$J_{i, j}^{k} = \frac{α [dis (X, Y)]}{β (S_{i}^{k} + S_{j}^{k})}$ (4)

式(4)中, α 为距离系数, β 为方差系数, 通过调整α 和β 使可区分函数值 $J_{i, j}^{k}$ 基本位于[0, 1], 可区分函数随着dis(X, Y)增加而增大。 $J_{i, j}^{k}$ 越大说明可分度越大, 有利于异纤检测。

1.3.2 自适应波段选择算法

传统自适应波段选择算法中仅考量了相邻波段间的相关性, 未对其他波段间的相关性做出说明; 本工作对自适应波段选择算法进行改进, 引入子波段平均相关性完善自适应指标, 进而建立ABS指数I_i。

$I_{i} = \frac{S_{i}}{(R_{i - 1, i}, R_{i, i + 1}, {\overset{̅}{R}}_{i}) / 3}$ (5)

$R_{ij} = \frac{\overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} [w_{i} - {\overset{̅}{w}}_{i}] [w_{j} - {\overset{̅}{w}}_{j}]}{\sqrt[]{(\overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} [w_{i} - {\overset{̅}{w}}_{i}]^{2}) \overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} [w_{j} - {\overset{̅}{w}}_{j}]^{2}}}$ (6)

${\overset{̅}{w}}_{i} = \frac{\overset{n}{\sum_{i = m}} w_{i}}{(n - m) + 1}$ (7)

其中, R_i_,_j为波段i与波段j的相关系数, ${\overset{̅}{R}}_{i}$ 为波段i与非相邻波段相关系数的均值, ${\overset{̅}{w}}_{i}$ 为波段i的均值。

1.3.3 区间值直觉模糊幂等麦考劳林对称平均聚合算子

为解决多种异纤的最佳波段选取问题, 综合考虑多类属性评价指标, 引入多属性群决策方法。由于异纤光谱特性中的吸收率和反射率之和小于1, 而IVIFS的适用范围完全满足, 同时考虑到输入参量间关系, 利用PA算子消若极端输入参数产生的负面影响, 使用MSM算子综合考量数据间的交互关系, 并将PA和MSM算子融入到区间值直觉模糊框架中, 提出基于WIVIFPMSM算子的异纤波段综合因素确定方法, 实现最佳波段选取。

令(α ₁, α ₂, …, α _n)为一个非负实数集, α _i=([ $u_{i}^{L}$ , $u_{i}^{U}$ ], [ $v_{i}^{U}$ , $v_{i}^{L}$ ]), α _i> 0, i=1, 2, …, n, WIVIFPMSM聚合算子的映射定义为

$\begin{array}{l} WIVIFPMS M^{(k)} (α_{1}, α_{2}, \dots, α_{n}) = {(\frac{\sum_{1 \leq i_{1} \leq i_{2} \dots \leq i_{n}} \overset{k}{\prod_{j = 1}} n η_{ij} α_{ij}}{C_{n}^{k}})}^{\frac{1}{k}} = \\ (\begin{array}{l} [{(1 - {(\prod_{1 \leq i_{1} \leq i_{2} \dots \leq i_{k} \leq n} (1 - \overset{k}{\prod_{j = 1}} 1 - (1 - u_{ij}^{L})^{n η_{ij}}))}^{\frac{1}{C_{n}^{k}}})}^{\frac{1}{k}}, {(1 - {(\prod_{1 \leq i_{1} \leq i_{2} \dots \leq i_{k} \leq n} (1 - \overset{k}{\prod_{j = 1}} 1 - (1 - u_{ij}^{U})^{n η_{ij}}))}^{\frac{1}{C_{n}^{k}}})}^{\frac{1}{k}}] \\ [1 - {(1 - \prod_{1 \leq i_{1} \leq i_{2} \dots \leq i_{k} \leq n} {(1 - \overset{k}{\prod_{j = 1}} (1 - (v_{ij}^{L})^{n η_{ij}}))}^{\frac{1}{C_{n}^{k}}})}^{\frac{1}{k}}, 1 - {(1 - \prod_{1 \leq i_{1} \leq i_{2} \dots \leq i_{k} \leq n} {(1 - \overset{k}{\prod_{j = 1}} (1 - (v_{ij}^{U})^{n η_{ij}}))}^{\frac{1}{C_{n}^{k}}})}^{\frac{1}{k}}] \end{array}) \end{array}$ (8)

式(8)中, k是一个非负整数, $(i_{1}, i_{2}, \dots, i_{k})$ 是 $(1, 2, \dots, n)$ 的任意k阶组合, $η_{ij} = \frac{w_{i} (1 - T (α_{ij}))}{\overset{n}{\sum_{m = 1}} w_{m} (1 - T (α_{m}))}, 0 \leq w_{m} \leq 1, \overset{n}{\sum_{m = 1}} w_{m} = 1, T (α_{i}) = \overset{n}{\sum_{\begin{array}{l} j = 1 \\ j \neq i \end{array}}} Sup (α_{i}, α_{j}), Sup (α_{i}, α_{j}) = 1 - D (α_{i}, α_{j}), C_{n}^{k}$ 是二项式系数。

分析两个区间值直觉模糊数(IVIFNs), 当隶属度区间和非隶属度区间完全一致, 两者才能够相等。仅靠得分函数S(α _i)和精度函数H(α _i)不能保证评价准则结果的准确性, 无法满足评价函数个数等于未知参数个数的要求, 方程组的解不唯一。考虑区间范围对结果的影响, 基于区间Pythagorean模糊信息进行评价函数诱导^[17], 其中, 隶属度范围越大说明非隶属度范围越小、不确定性越大, 引入IVIFNs的隶属度不确定函数Mu(α _i), 结合犹豫度π (a_i)=( $π_{i}^{L}$ , $π_{i}^{U}$ ), 提出犹豫度不确定函数Hu(α _i), 具体公式为

$S (α_{i}) = \frac{1}{2} (μ_{i}^{L} + μ_{i}^{U} - v_{i}^{L} - v_{i}^{U})$ (9)

$H (α_{i}) = \frac{1}{2} (μ_{i}^{L} + μ_{i}^{U} + v_{i}^{L} + v_{i}^{U})$ (10)

$Mu (α_{i}) = u_{i}^{U} - u_{i}^{L} - (v_{i}^{U} - v_{i}^{L})$ (11)

$Hu (α_{i}) = u_{i}^{U} - u_{i}^{L} + v_{i}^{U} - v_{i}^{L}$ (12)

对于任意一组评价函数S(α _i)、 H(α _i)、 Mu(α _i)和Hu(α _i), 构造非齐次线性方程组, 通过研究方程组解的情况, 判定评价准则的严谨性, 为构建精准的评价准则提供前提, 有利于决策结果的准确性。增广矩阵如式(13)所示, 增广矩阵的秩Rank(A)=4, 等于变量 $μ_{i}^{L}$ 、 $μ_{i}^{U}$ 、 $v_{i}^{L}$ 、 $v_{i}^{U}$ 的个数, 因此评价函数方程组有唯一解, 可以区分任意两个IVIFNs。

$A = (\begin{array}{l} 1 & 1 & - 1 & - 1 & 2 S \\ 0 & 2 & 0 & 2 & Mu - 2 S \\ 0 & 0 & 2 & 2 & 2 H - 2 S \\ 0 & 0 & 0 & 4 & 2 H + Hu - Mu - 2 S \end{array})$ (13)

根据IVIFNs的四个指标函数S(α _i)、 H(α _i)、 Mu(α _i)和Hu(α _i), 定义任意两个IVIFNs的评价准则: 若S(α ₁)> S(α ₂), 则α ₁> α ₂; 若S(α ₁)< S(α ₂), 则α ₁< α ₂; 若S(α ₁)=S(α ₂), 使用H(α _i)函数比较: 若H(α ₁)> H(α ₂), 则α ₁> α ₂; 若H(α ₁)< H(α ₂), 则α ₁< α ₂; 若H(α ₁)=H(α ₂), 使用Mu(α _i)函数比较: 若Mu(α ₁)> Mu(α ₂), 则α ₁< α ₂; 若Mu(α ₁)< Mu(α ₂), 则α ₁> α ₂; 若Mu(α ₁)=Mu(α ₂), 使用Hu(α _i)函数比较: 若Hu(α ₁)> Hu(α ₂), 则α ₁< α ₂; 若Hu(α ₁)< Hu(α ₂), 则α ₁> α ₂; 若Hu(α ₁)=Hu(α ₂), 则α ₁=α ₂。

1.3.4 拓展优劣解距离法

优劣解距离法(TOPSIS)^[16]可实现多输入参数的综合评价, 为了确定出异纤光谱决策信息的相关权重分布, 将TOPSIS方法进行扩展, 与区间值直觉模糊集结合, 诱导相应决策数据下的理想矩阵和贴近度。令X={X₁, X₂, …, X_m}为方案集, A={A₁, A₂, …, A_n}为属性集, D={D₁, D₂, …, D_s}为决策集合。任意X_i对A_j的评价信息为 $a_{ij}^{k}$ =([ $u_{ij}^{Lk}$ , $u_{ij}^{Uk}$ ], [ $v_{ij}^{Uk}$ , $v_{ij}^{Lk}$ ]), IVIFS决策信息简记为D_m_×_n。

根据决策矩阵 ${D_{m \times}}_{n}$ 获得正理想矩阵D^*和3个负理想矩阵D^-、 D⁺和(D^*)^c, 矩阵为

$D_{ij}^{*} = (D_{ij}^{*})_{m \times n} = ([μ_{ij}^{L *}, μ_{ij}^{U *}], [v_{ij}^{L *}, v_{ij}^{U *} {])}_{m \times n}$ (14)

$D^{-} = (D_{ij}^{-})_{m \times n} = ([μ_{ij}^{L -}, μ_{ij}^{U -}], [ν_{ij}^{L -}, ν_{ij}^{U -} {])}_{m \times n}$ (15)

$D^{+} = (D_{ij}^{+})_{m \times n} = ([μ_{ij}^{L +}, μ_{ij}^{U +}], [ν_{ij}^{L +}, ν_{ij}^{U +} {])}_{m \times n}$ (16)

$(D^{*})^{c} = ((D_{ij}^{*})^{c})_{m \times n} = ([ν_{ij}^{L *}, ν_{ij}^{U *}], [μ_{ij}^{L *}, μ_{ij}^{U *} {])}_{m \times n}$ (17)

式中

$\begin{array}{l} μ_{ij}^{L *} = {(1 - \overset{t}{\prod_{k = 1}} (1 - (μ_{ij}^{L (k)})^{2})^{1 / t})}^{1 / 2}, \\ μ_{ij}^{U *} = {(1 - \overset{t}{\prod_{k = 1}} (1 - (μ_{ij}^{U (k)})^{2})^{1 / t})}^{1 / 2}, \\ v_{ij}^{L *} = \overset{t}{\prod_{k = 1}} (μ_{ij}^{L (k)})^{1 / t}, v_{ij}^{U *} = \overset{t}{\prod_{k = 1}} ({μ_{U (k)}}_{ij})^{1 / t}, \\ μ_{ij}^{L -} = \min_{k = 1, 2, \dots, t} {μ_{ij}^{L (k)}}, \\ μ_{ij}^{U -} = \min_{k = 1, 2, \dots, t} {μ_{ij}^{U (k)}}, v_{ij}^{L -} = \max_{k = 1, 2, \dots, t} {v_{ij}^{L (k)}}, \\ v_{ij}^{U -} = \max_{k = 1, 2, \dots, t} {v_{ij}^{U (k)}}, μ_{ij}^{L +} = \max_{k = 1, 2, \dots, t} {μ_{ij}^{L (k)}}, \\ μ_{ij}^{U +} = \max_{k = 1, 2, \dots, t} {μ_{ij}^{U (k)}}, v_{ij}^{L +} = \min_{k = 1, 2, \dots, t} {v_{ij}^{L (k)}} 。 \end{array}$

根据正理想矩阵和负理想矩阵, 计算其贴近度。

$R C_{k} = \frac{Npro j_{D^{*}} (D^{(k)})}{Npro j_{D^{*}} (D^{(k)}) + Npro j_{D^{-}} (D^{(k)}) + Npro j_{D^{+}} (D^{(k)}) + Npro j_{(D^{*})^{C}} (D^{(k)})}$ (18)

决策矩阵离正理想矩阵越近, 离负理想矩阵就越远, 相对贴近度就越大, 通过值的归一化计算权重矩阵。

$w_{k} = \frac{R C_{k}}{\overset{t}{\sum_{k = 1}} R C_{k}}$ (19)

2 结果与讨论

2.1 异性纤维波段划分

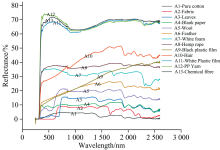
对采集的异性纤维波段数据进行统计分析, 使用数据的均值作为有效数据, 以保证后续实验的可靠性, 异纤光谱具体信息如图1所示。丙纶丝、化学纤维和白色塑料薄膜的反射率明显高于其他异性纤维, 并且在波段380~1 100 nm有较好的辨识率, 但是整体差异性较小。波段240~715 nm棉花与布块、树叶的反射率差在5%之内, 可识别性小不利于检测。黑色塑料薄膜和头发的反射率收敛较慢, 在波段240~1 700 nm持续增长。另外, 可以看到棉花与主要异性纤维的可辨识性明显, 有利于检测识别。而棉花与羊毛在波段300~700 nm可分性和棉花与布块在波段300~715 nm和波段2 200~2 450 nm的可分性较差。根据光谱学划分方法, 将波段划分为: W₁: 240~380 nm、 W₂: 380~780 nm、 W₃: 780~1 100 nm、 W₄: 1 100~1 700 nm、 W₅: 1 700~2 100 nm、 W₆: 2 100~2 600 nm。

	Figure Option View Download New Window
	图1 棉花与异性纤维反射率图像Fig. 1 Reflectance spectra of cotton and foreign fibers

2.2 基于类间可分的异性纤维波段划分方法

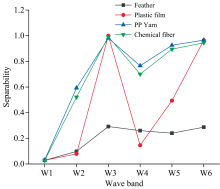
为提高异纤检测效果, 对异纤与棉花间的可区分性进行分析, 如图2所示, 羽毛、塑料薄膜、丙纶丝以及化学纤维均在波段W₃取得最大可分度, 其中塑料薄膜的可分度为1, 说明塑料薄膜在波段W₃达到完全可分的效果。另外, 主要异纤在波段W₃的可分效果明显高于波段W₁、 W₂、 W₄和W₅, 有利于棉花中异纤检测。

	Figure Option View Download New Window
	图2 棉花与主要异性纤维可分度Fig.2 Separabilities of cotton and main foreign fibers

2.3 基于信息量的异性纤维波段划分方法

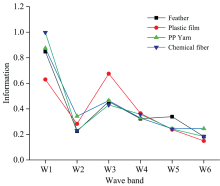
自适应波段选择算法通过考察波段间的相关性, 对信息量做出保证, 同时该方法不需要预先确定波段个数, 提供多种波段划分选择。异纤经过ABS算法处理获得各波段ABS指标图像, 如图3所示。由于波段间的信息量与波段数据的标准差有关, 在检测初期, 反射率发生剧烈变化, 造成初始阶段W₁的波间信息较大。当反射率趋于稳定, 信息量在波段W₃达到最大, 另外, 塑料薄膜在波段W₃的信息量大于在波段W₁处的信息量。因此, 在保证数据稳定的前提下, 波段W₃各类异性纤维的信息量达到最大化。

	Figure Option View Download New Window
	图3 主要异性纤维在波段W₁— W₆信息量Fig.3 The main foreign fibers information in W₁— W₆ wave bands

2.4 基于多属性决策方法在异性纤维波段划分中的应用

针对棉花中异纤检测最佳波段选取问题, 采用WIVIFPMSM算子聚合多种异纤的波段决策信息, 拓展TOPSIS方法确定异纤权重向量, 利用评价准则确定最佳波段信息。使用羽毛、塑料薄膜、丙纶丝、化学纤维四类异纤, 构建F={F₁, F₂, F₃, F₄}, 对6个子波段W={W₁, W₂, W₃, W₄, W₅, W₆}, 在3种属性A={A₁, A₂, A₃}下进行评价, 其中A₁表示类间可分度, A₂表示相关性, A₃表示信息量, 异纤权重向量为w'={w'₁, w'₂, w'₃, w'₄, w'₅, w'₆}, 属性权重为w={w₁, w₂, w₃}, 考虑到属性的相对独立性, 设定w={0.333, 0.333, 0.333}。利用评价信息获得决策矩阵, 使用评价值作为直觉模糊集的隶属度, 非隶属度取直觉模糊环境下的最大值, 由于数据采集及处理过程中存在误差, 将直觉模糊集转变为区间值直觉模糊集, 如表1— 表4所示。

表1 羽毛决策矩阵

F_{m \times n}^{1}

Table 1 The decision matrix

F_{m \times n}^{1}

of the feather

波段	羽毛属性
波段	可分度	相关性	ABS指标
W₁	([0.026, 0.029], [0.874, 0.971])	([0.635, 0.705], [0.265, 0.295])	([0.763, 0.848], [0.137, 0.152])
W₂	([0.088, 0.098], [0.812, 0.902])	([0.556, 0.618], [0.344, 0.382])	([0.203, 0.225], [0.698, 0.775])
W₃	([0.263, 0.292], [0.637, 0.708])	([0.843, 0.937], [0.057, 0.063])	([0.411, 0.457], [0.489, 0.543])
W₄	([0.234, 0.260], [0.666, 0.740])	([0.787, 0.875], [0.113, 0.125])	([0.291, 0.323], [0.609, 0.677])
W₅	([0.216, 0.240], [0.684, 0.760])	([0.648, 0.720], [0.252, 0.280])	([0.305, 0.339], [0.595, 0.661])
W₆	([0.259, 0.287], [0.641, 0.713])	([0.898, 0.997], [0.002, 0.003])	([0.164, 0.183], [0.736, 0.817])

表1 羽毛决策矩阵

F_{m \times n}^{1}

Table 1 The decision matrix

F_{m \times n}^{1}

of the feather

表2 塑料薄膜决策矩阵

F_{m \times n}^{2}

Table 2 The decision matrix

F_{m \times n}^{2}

of the plastic film

波段	塑料薄膜属性
波段	可分度	相关性	ABS指标
W₁	([0.025, 0.029], [0.875, 0.971])	([0.524, 0.583], [0.376, 0.417])	([0.567, 0.630], [0.333, 0.370])
W₂	([0.071, 0.079], [0.829, 0.921])	([0.730, 0.811], [0.170, 0.189])	([0.255, 0.283], [0.645, 0.717])
W₃	([0.900, 1.000], [0.000, 0.000])	([0.882, 0.981], [0.018, 0.020])	([0.608, 0.675], [0.293, 0.325])
W₄	([0.131, 0.146], [0.769, 0.854])	([0.830, 0.922], [0.112, 0.124])	([0.329, 0.365], [0.572, 0.635])
W₅	([0.445, 0.494], [0.455, 0.506])	([0.657, 0.730], [0.243, 0.270])	([0.215, 0.238], [0.685, 0.762])
W₆	([0.869, 0.965], [0.031, 0.035])	([0.893, 0.992], [0.007, 0.008])	([0.134, 0.149], [0.766, 0.851])

表2 塑料薄膜决策矩阵

F_{m \times n}^{2}

Table 2 The decision matrix

F_{m \times n}^{2}

of the plastic film

表3 丙纶丝决策矩阵

F_{m \times n}^{3}

Table 3 The decision matrix

F_{m \times n}^{3}

of the PP Yarn

波段	丙纶丝属性
波段	可分度	相关性	ABS指标
W₁	([0.028, 0.032], [0.872, 0.968])	([0.493, 0.548], [0.407, 0.452])	([0.788, 0.875], [0.113, 0.125])
W₂	([0.534, 0.593], [0.366, 0.407])	([0.717, 0.796], [0.183, 0.204])	([0.308, 0.342], [0.592, 0.658])
W₃	([0.883, 0.981], [0.017, 0.019])	([0.878, 0.975], [0.023, 0.025])	([0.419, 0.465], [0.482, 0.535])
W₄	([0.689, 0.766], [0.211, 0.234])	([0.788, 0.876], [0.112, 0.124])	([0.295, 0.328], [0.605, 0.672])
W₅	([0.833, 0.926], [0.067, 0.074])	([0.520, 0.578], [0.380, 0.422])	([0.219, 0.244], [0.681, 0.756])
W₆	([0.869, 0.966], [0.031, 0.034])	([0.897, 0.997], [0.002, 0.003])	([0.221, 0.245], [0.679, 0.755])

表3 丙纶丝决策矩阵

F_{m \times n}^{3}

Table 3 The decision matrix

F_{m \times n}^{3}

of the PP Yarn

表4 化学纤维决策矩阵

F_{m \times n}^{4}

Table 4 The decision matrix

F_{m \times n}^{4}

of the chemical fiber

波段	化学纤维属性
波段	可分度	相关性	ABS指标
W₁	([0.025, 0.028], [0.875, 0.972])	([0.664, 0.738], [0.236, 0.262])	([0.898, 0.998], [0.001, 0.002])
W₂	([0.470, 0.522], [0.430, 0.478])	([0.503, 0.559], [0.397, 0.441])	([0.208, 0.231], [0.692, 0.769])
W₃	([0.894, 0.993], [0.006, 0.007])	([0.878, 0.976], [0.022, 0.024])	([0.388, 0.431], [0.512, 0.569])
W₄	([0.631, 0.701], [0.269, 0.299])	([0.821, 0.912], [0.079, 0.088])	([0.321, 0.357], [0.579, 0.643])
W₅	([0.805, 0.895], [0.095, 0.105])	([0.360, 0.400], [0.540, 0.600])	([0.218, 0.242], [0.682, 0.758])
W₆	([0.851, 0.945], [0.049, 0.055])	([0.898, 0.997], [0.002, 0.003])	([0.166, 0.184], [0.734, 0.816])

表4 化学纤维决策矩阵

F_{m \times n}^{4}

Table 4 The decision matrix

F_{m \times n}^{4}

of the chemical fiber

考虑到异纤之间的相互作用, 避免极端数据的负面影响, 利用TOPSIS方法确定各类异性纤维的权重向量。使用决策矩阵, 计算决策矩阵F⁽^k⁾在正理想矩阵F^*和负理想矩阵F⁺、 F^-、 (F^*)^c上的投影, 其结果如表5所示。

表5

F_{m \times n}^{k}

在理想决策矩阵上的投影 Table 5 The projection of

F_{m \times n}^{k}

in ideal decision matrix

理想矩阵	决策矩阵
理想矩阵	F¹	F²	F³	F⁴
F^*	0.801	0.890	0.959	0.938
F⁺	0.708	0.818	0.974	0.980
F^-	0.957	0.813	0.501	0.692
(F^*)^c	0.388	0.272	0.460	0.251

表5

F_{m \times n}^{k}

在理想决策矩阵上的投影 Table 5 The projection of

F_{m \times n}^{k}

in ideal decision matrix

根据式(19)计算各类异纤的贴近度RC₁=0.281, RC₂=0.319, RC₃=0.331, RC₄=0.328, 将贴近度进行归一化, 获得权重w'₁=0.223, w'₂=0.253, w'₃=0.263, w'₄=0.261, 所以异纤权重向量为w'₁=(0.223, 0.253, 0.263, 0.261)。

计算支持矩阵Sup( $α_{ij}^{d}$ , $α_{ik}^{l}$ ), 为方便将 $α_{ij}^{d}$ 对 $α_{ik}^{l}$ 的支持矩阵Sup( $α_{ij}^{d}$ , $α_{ik}^{l}$ )记为S_dl。

$\begin{array}{l} S_{12} = S_{21} = [\begin{array}{l} 0.999 & 0.883 & 0.793 \\ 0.982 & 0.816 & 0.945 \\ 0.328 & 0.958 & 0.793 \\ 0.892 & 0.955 & 0.960 \\ 0.759 & 0.990 & 0.905 \\ 0.356 & 0.995 & 0.968 \end{array}] \\ S_{13} = S_{31} = [\begin{array}{l} 0.998 & 0.850 & 0.974 \\ 0.530 & 0.830 & 0.889 \\ 0.346 & 0.964 & 0.992 \\ 0.520 & 0.999 & 0.996 \\ 0.349 & 0.865 & 0.910 \\ 0.356 & 0.999 & 0.941 \end{array}] \\ S_{14} = S_{41} = [\begin{array}{l} 0.375 & 1.000 & 0.999 \\ 0.378 & 0.696 & 0.908 \\ 0.581 & 0.964 & 0.968 \\ 0.334 & 0.963 & 0.975 \\ 0.597 & 0.944 & 0.994 \\ 0.999 & 0.969 & 0.857 \end{array}] \\ S_{23} = S_{32} = [\begin{array}{l} 0.997 & 0.967 & 0.767 \\ 0.512 & 0.986 & 0.944 \\ 0.982 & 0.995 & 0.801 \\ 0.411 & 0.956 & 0.965 \\ 0.590 & 0.855 & 0.995 \\ 1.000 & 0.996 & 0.909 \end{array}] \\ S_{24} = S_{42} = [\begin{array}{l} 1.000 & 0.853 & 0.650 \\ 0.579 & 0.761 & 0.951 \\ 0.994 & 0.995 & 0.768 \\ 0.473 & 0.991 & 0.992 \\ 0.620 & 0.678 & 0.997 \\ 0.981 & 0.995 & 0.967 \end{array}] \\ S_{34} = S_{43} = [\begin{array}{l} 0.997 & 0.819 & 0.883 \\ 0.933 & 0.775 & 0.895 \\ 0.989 & 0.999 & 0.968 \\ 0.939 & 0.965 & 0.972 \\ 0.971 & 0.831 & 0.998 \\ 0.981 & 0.999 & 0.942 \end{array}] \end{array}$

根据支持函数Sup( $α_{ij}^{d}$ , $α_{ik}^{l}$ )求解加权支持矩阵T( $α_{ij}^{d}$ ), 计算幂权重矩阵 $λ_{ij}^{d}$ , 记作λ _d。

$\begin{array}{l} λ_{1} = [\begin{array}{l} 0.214 & 0.215 & 0.219 \\ 0.214 & 0.215 & 0.214 \\ 0.177 & 0.212 & 0.217 \\ 0.216 & 0.214 & 0.214 \\ 0.199 & 0.216 & 0.209 \\ 0.179 & 0.214 & 0.215 \end{array}] \\ λ_{2} = [\begin{array}{l} 0.253 & 0.254 & 0.243 \\ 0.251 & 0.253 & 0.254 \\ 0.266 & 0.253 & 0.242 \\ 0.245 & 0.252 & 0.252 \\ 0.257 & 0.255 & 0.254 \\ 0.266 & 0.252 & 0.252 \end{array}] \\ λ_{3} = [\begin{array}{l} 0.261 & 0.260 & 0.268 \\ 0.259 & 0.263 & 0.258 \\ 0.275 & 0.262 & 0.266 \\ 0.261 & 0.261 & 0.261 \\ 0.266 & 0.205 & 0.263 \\ 0.274 & 0.261 & 0.259 \end{array}] \\ λ_{4} = [\begin{array}{l} 0.260 & 0.258 & 0.257 \\ 0.263 & 0.256 & 0.261 \\ 0.273 & 0.260 & 0.262 \\ 0.265 & 0.260 & 0.260 \\ 0.267 & 0.250 & 0.261 \\ 0.272 & 0.260 & 0.261 \end{array}] \end{array}$

利用IVIFPMSM算子将决策矩阵D₁, D₂, D₃, D₄聚合成一个IVIFS决策矩阵D'=(α _ij)_{6× 3}, 综合决策矩阵D'见表6。

表6 综合决策矩阵D' Table 6 The integrated decision matrix D'

计算D'_m_×_n(α _ij)中α _ij, α _ik(j, k=1, 2, 3; j≠ k)支持函数Sup'(α _ij, α _ik), 简记为S'_jk。

$\begin{array}{l} S'_{12} = S'_{21} = [\begin{array}{l} 0.693 \\ 0.986 \\ 0.140 \\ 0.655 \\ 0.729 \\ 0.175 \end{array}] \\ S'_{13} = S'_{31} = [\begin{array}{l} 0.224 \\ 0.961 \\ 0.586 \\ 0.881 \\ 0.610 \\ 0.349 \end{array}] \\ S'_{23} = S'_{32} = [\begin{array}{l} 0.531 \\ 0.975 \\ 0.554 \\ 0.774 \\ 0.881 \\ 0.826 \end{array}] \end{array}$

根据支持函数Sup'(α _ij, α _ik)求解加权支持矩阵T'(α _ij), 计算幂权重矩阵η _ij。

$η_{ij} = [\begin{array}{l} 0.329 & 0.355 & 0.316 \\ 0.333 & 0.334 & 0.333 \\ 0.322 & 0.320 & 0.358 \\ 0.333 & 0.325 & 0.342 \\ 0.323 & 0.343 & 0.334 \\ 0.301 & 0.342 & 0.357 \end{array}]$

利用IVIFPMSM算子将决策矩阵D'中的α _ij聚合为α _i, 聚合矩阵如表7所示。

表7 聚合矩阵 Table 7 The aggregation matrix

计算S(α _i)、 H(α _i)、 Mu(α _i)和Hu(α _i), 按评价准则进行排序。得分函数计算结果为: S(W₁)=-0.273, S(W₂)=-0.401, S(W₃)=-0.074, S(W₄)=-0.404, S(W₅)=-0.142, S(W₆)=-0.466, 根据第一评价准则进行排序, 排序结果为W₃> W₅> W₁> W₂> W₄> W₆, 即最佳波段为近红外波段W₃。

2.5 敏感度分析

参数k的取值会对最终的决策结果产生影响, 研究不同k值下WIVIFPMSM算子决策结果的敏感性, 如表8所示。尽管k被赋值为不同的数值, 但最佳的波段均为W₃, 不同参数k下决策结果的一致性说明了所提方法具有一定的稳定性。在实际决策中, 可选择合适的k值, 即根据决策风险的程度选择参数k的自适应值。对参数k进行敏感性分析, 若优先考虑风险, 则WIVIFPMSM算子的参数k将尽可能大; 如不考虑风险, 则尽量减小参数k。

表8 不同k值对决策结果的影响 Table 8 The influences of different k values on decision results

2.6 方法比较

分析基于WIVIFPMSM算子异纤最佳波段选择结果与ISBC和ABS方法的差异, 如表9所示。 ISBC方法表示异纤与棉花的类间可分程度, 当使用该方法时, 4种主要异纤的最佳波段均为W₃, 最差波段均为W₁; ABS方法可以显示波段所包含的信息量, 波段间的标准差对最终的结果存在影响, 在使用ABS方法进行波段选择时, 只有塑料薄膜的最佳波段为W₃, 羽毛、丙纶丝和化学纤维的最佳波段为W₁, 其主要原因是异纤光谱信息在采集初期的波段波动较大, 较大标准差造成了异纤在波段W₁包含信息量较大, 但是在波段稳定后, 各类异纤最佳波段均为W₃。基于WIVIFPMSM算子将类间可分度、相关性和信息量综合考虑, 对异纤的最佳波段进行多方面分析, 发现最佳波段为W₃, 与上述ISBC和ABS方法结果一致。进一步比较最佳决策结果同次等结果的差异突显所提多属性决策方法优势, 发现所提方法较ISBC方法下的主要异纤平均差异提升88.89%, 在不考虑波段W₁下所提方法较ABS方法下的主要异纤平均差异提升67.23%。通过将多属性决策方法与传统划分方法比较, 说明了所提方法的有效性, 且多属性决策方法较传统方法能实现波段信息综合评价, 聚合多种评价信息, 为后续多角度指标的精确波长确定提供一种可行性方案。

表9 多属性决策方法与传统划分方法比较 Table 9 Comparison the decision-making method with the traditional method

3 结论

针对波段传统划分方法指标单一缺陷, 综合考虑可分度、相关性和信息量等属性评价指标, 提出一种异纤波段多属性决策方法, 并将决策结果与传统波段划分方法结果进行对比, 说明所提方法的合理性和有效性。研究了传统波段划分方法并进行改进, 通过使用平均欧式距离进行距离度量优化ISBC法, 利于增加目标波段与非相邻波段的相关系数改进基于信息量的ABS法。诱导WIVIFPMSM模糊聚合算子, 使用拓展TOPSIS法优化决策过程中的权重分布, 构建多属性决策机制, 并将其应用到异纤最佳波段的选取中, 以类间可分性、相关性和信息量等性质为属性集, 以4种主要异纤为决策集, 实现最佳波段的选取。通过决策结果的敏感度分析和方法比较体现决策机制优越性, 发现不同k值下的最佳决策结果一致, 说明所提多属性决策方法具有较好稳定性。将基于WIVIFPMSM算子的决策结果与传统波段划分方法对比, 决策结果一致, 处理结果有效, 然而所提方法能够改善单一波段划分方法信息量的局限性, 从多角度、多属性进行最佳光谱特性的选取, 为后续精确波长确定提供一种有效的决策方案。

参考文献

文献列表

[1]	REN Wei-jia, DU Yu-hong, ZUO Heng-li, et al(任维佳, 杜玉红, 左恒力, 等). Journal of Textile Research(纺织学报), 2021, 42(12): 196. [本文引用:1]
[2]	ZHANG Lin, WEI Ping, WU Jian-bo, et al(张林, 韦平, 伍剑波, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2016, 32(15): 289. [本文引用:1]
[3]	SHI Hong-yu, GUAN Sheng-qi (师红宇, 管声启). Journal of Donghua University(Natural Science) [东华大学学报(自然科学版)], 2016, 42(3): 400. [本文引用:1]
[4]	Bao S, Cao C, Chen W, et al. Geocarto International, 2021, 36(2): 226. [本文引用:1]
[5]	Charifi R, Es-Sbai N, Zennayi Y, et al. Computers & Geosciences, 2021, 150: 104696. [本文引用:1]
[6]	YANG Wen-zhu, LI Dao-liang, WEI Xin-hua, et al(杨文柱, 李道亮, 魏新华, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2009, 25(10): 186. [本文引用:1]
[7]	JIA Dong-yao, DING Tian-huai (郏东耀, 丁天怀). Journal of Tsinghua University(Science and Technology) [清华大学学报(自然科学版)], 2005, 2: 193. [本文引用:1]
[8]	Jiang Y, Li C. Computers and Electronics in Agriculture, 2015, 119: 191. [本文引用:2]
[9]	Wang Q, Li Q, Li X. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(12): 4940. [本文引用:1]
[10]	YANG Sai, ZHU Qi-bing, HUANG Min(杨赛, 朱启兵, 黄敏). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2017, 37(3): 990. [本文引用:1]
[11]	MA Meng-ru, ZHANG Yong-bin, WANG Yi-dan (马梦茹, 张永彬, 王奕丹). Journal of North China University of Science and Technology(Natural Science Edition) [华北理工大学学报(自然科学版)], 2021, 43(3): 20. [本文引用:1]
[12]	Ali Z, Mahmood T. Computational and Applied Mathematics, 2020, 39: 161. [本文引用:1]
[13]	Yager R R. IEEE Transactions on Systems, 2001, 31(6): 724. [本文引用:1]
[14]	Zindani D, Maity S R, Bhowmik S. Soft Computing, 2020, 24(18): 114091. [本文引用:1]
[15]	Liu Z, Teng F, Liu P, et al. International Journal for Uncertainty Quantifications, 2018, 8(3): 211. [本文引用:1]
[16]	Garg H, Ali Z, Mahmood T. Expert Systems, 2021, 38(1): e12609. [本文引用:2]
[17]	Ren W, Du Y. Journal of Natural Fibers, 2023, 20(2): 2219906. [本文引用:3]

2021

0.0

... 棉花中的异性纤维(简称异纤)不仅会造成纱线的断裂, 更影响织物的质量, 造成纺织企业巨大经济损失^[1] ...

2016

0.0

... 目前主要采用图像处理的方法^[2,3]实现棉花中异纤的检测, 利用特定光源照射棉花, 通过将CCD采集到的图像进行数据处理, 找出与棉纤维的差异识别异纤 ...

2016

0.0

2021

0.0

... Bao等^[4]分析单因素方差和Jeffries-Matusita(J-M)距离光谱一致性检验, 并利用J-M距离选取最佳波段 ...

2021

0.0

... Charifi等^[5]利用Bhattacharyya距离进行可分性检验, 根据可分度选择波段组合 ...

2009

0.0

... 杨文柱等^[6]利用波段间的类间可分性, 认定780~1 800 nm的近红外波段为最佳检测波段 ...

2005

0.0

... 郏东耀^[7]采用基于区域信息相关度权值小波分析算法将多个波段的信息进行融合, 提出了一种利用多波段光谱信息融合成像检测的新方法 ...

2015

0.0

... Jiang等^[8]采用最小冗余最大相关性(mRMR)算法选择最优波长, 提高棉花中异纤的分类效果 ...

... 针对12类异纤进行光谱数据采集, 每类异纤采集10组数据信息, 数据采集过程中按颜色、厚度、疏密度对样本进行调整^[8] ...

2019

0.0

... Wang等^[9]提出了一种基于自适应子空间划分策略(ASPS)波段选择方法 ...

2017

0.0

... 杨赛等^[10]发现平均光谱和熵联合的分类精度高于单一特征模型, 为波段融合方法提供了理论基础 ...

2021

0.0

... 马梦茹等^[11]利用OIF和ABS方法进行最佳波段选取, ABS比OIF方法提升精度9 ...

2020

0.0

... 本工作引入多属性决策法, 利用MSM算子^[12]综合考量多个输入参数交互关系, 使用PA算子^[13]削弱极端输入参数的优势, 提出WIVIFPMSM聚合算子^[14,15,16], 结合TOPSIS确定各类异性纤维权重向量^[17], 构建最佳波段的多属性决策框架, 实现最佳波段的选取 ...

2001

0.0

2020

0.0

2018

0.0

2021

0.0

... 优劣解距离法(TOPSIS)^[16]可实现多输入参数的综合评价, 为了确定出异纤光谱决策信息的相关权重分布, 将TOPSIS方法进行扩展, 与区间值直觉模糊集结合, 诱导相应决策数据下的理想矩阵和贴近度 ...

2023

0.0

... 实验样本来源于湖北谷城银纺公司等全国10个棉纺企业实际生产中剔除的异纤, 经初步检查有布块、树叶、白纸、羊毛、羽毛、白色泡沫、麻绳、黑色塑料薄膜、头发、白色塑料薄膜、丙纶丝、化学纤维等多种异纤, 而羽毛、塑料薄膜、化学纤维、丙纶丝含量较多, 作为主要研究对象^[17] ...

... 考虑区间范围对结果的影响, 基于区间Pythagorean模糊信息进行评价函数诱导^[17], 其中, 隶属度范围越大说明非隶属度范围越小、不确定性越大, 引入IVIFNs的隶属度不确定函数Mu(#cod#x003b1 ...