引用本文
李浩, 赵青, 崔辰州, 樊东卫, 张成奎, 史艳翠, 王嫄. 基于CNN与LSTM复合深度模型的恒星光谱分类算法[J]. 光谱学与光谱分析, 2024,44(6): 1668-1675.
LI Hao, ZHAO Qing, CUI Chen-zhou, FAN Dong-wei, ZHANG Cheng-kui, SHI Yan-cui, WANG Yuan. A Stellar Spectrum Classification Algorithm Based on CNN and LSTM Composite Deep Learning Model[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1668-1675.
Doi:10.3964/j.issn.1000-0593(2024)06-1668-08  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于CNN与LSTM复合深度模型的恒星光谱分类算法
李浩1, 赵青1,*, 崔辰州2, 樊东卫2, 张成奎1, 史艳翠1, 王嫄1
1. 天津科技大学人工智能学院, 天津 300457
2. 中国科学院国家天文台, 北京 100012
*通讯作者 e-mail: zhaoqing@tust.edu.cn

作者简介: 李 浩, 1998年生, 天津科技大学人工智能学院硕士研究生 e-mail: 1287467828@qq.com

收稿日期: 2022-12-03 修回日期: 2023-09-15
基金: 国家自然科学基金青年科学基金项目(11803022), 国家自然科学基金面上项目(12273077), 国家重点研发计划项目(2022YFF0711500)资助
摘要

恒星光谱分类是天文学领域中非常重要的研究方向。 随着科技的迅猛发展, 大型巡天望远镜采集的恒星光谱数据已经达到了TB或甚至PB级别, 传统的分类方法已经无法满足如此庞大数据量的处理需求。 正确分类光谱对于研究恒星的物理性质以及演化过程具有重要意义。 CNN通过卷积运算学习数据的局部特征, 去除冗余信息, 并通过最大池化运算对特征进行压缩。 然而, 由于原始CNN模型的全连接层缺乏长距离依赖挖掘的功能, 如果加入LSTM网络, 通过其独特的三个“门”的远距离依赖挖掘能力可提取的重要特征, 并检测特征中的微小差异, 恰好可以解决这个问题。 因此, 提出了一种基于CNN和LSTM复合的深度模型, 用于对LAMOST DR8中的恒星光谱进行分类。 这种模型能够更好地学习恒星光谱的特征, 为恒星演化研究提供了重要的帮助。 为了提高模型的收敛速度, 使用了常见的Z-Score标准化方法对数据进行处理。 提出的模型在F、 G、 K三分类实验中取得了94.56%的分类准确率。 同时, 与前人使用过的RBM、 PILDNN、 PILDNN*、 DBN、 Inception v3、 1D-SSCNN、 LSTM方法进行对比, 结果表明该方法具有更高的分类准确率。 在十分类实验中, 该方法取得了97.35%的准确率, 并且相比于仅使用LSTM、 1D-SSCNN方法的实验结果, 该方法的结果更好, 且训练时间减少了近十倍。 使用F1-score对每类恒星光谱分类准确度进行说明, 在三分类和十分类实验中, 每类的F1值都在0.9以上。 与前人在文献中的实验结果进行对比, 该模型的结果更好。 通过混淆矩阵的结果, 可以得出该模型在光谱种类越多的实验中准确率越高, 甚至可以达到100%。 综上所述, 所提出的基于CNN和LSTM相结合的模型可以有效地对大规模恒星光谱数据进行分类, 并取得了优异的分类效果。

关键词: LAMOST; 恒星光谱分类; 卷积神经网络; 长短期记忆网络; Z-Score标准化
中图分类号:P157.2 文献标志码:A
A Stellar Spectrum Classification Algorithm Based on CNN and LSTM Composite Deep Learning Model
LI Hao1, ZHAO Qing1,*, CUI Chen-zhou2, FAN Dong-wei2, ZHANG Cheng-kui1, SHI Yan-cui1, WANG Yuan1
1. School of Artificial Intelligence, Tianjin University of Science and Technology, Tianjin 300457, China
2. National Astronomical Observatory, Chinese Academy of Sciences, Beijing 100012, China
*Corresponding author
Abstract

Stellar spectral classification is a significant research direction in astronomy. With the rapid development of technology, the stellar spectral data collected by large survey telescopes have reached terabytes or even petabytes, and the traditional classification methods can no longer meet the processing needs of such a vast amount of data. CNNs learn the local features of the data by convolution operations, remove redundant information, and compress the features by maximum pooling operations. However, since the fully-connected layer of the original CNN model lacks the function of long-range dependency mining, this problem can be solved by adding LSTM networks, which can extract important features and detect small differences in features through their unique three “gates” of long-range dependency mining capability. Therefore, this paper proposes a deep model based on the composite of CNN and LSTM for classifying stellar spectra in LAMOST DR8. This model can better learn the features of stellar spectra, which provides an important help for stellar evolution studies. To improve the convergence speed of the model, the common Z-Score normalization method is used to process the data. The model proposed in this paper achieved a classification accuracy of 94.56% in the F, G, and K classification experiments. Meanwhile, compared with the previously used RBM, PILDNN, PILDNN*, DBN, Inception v3, 1D-SSCNN, and LSTM methods, the results show that the method in this paper has a higher classification accuracy. In the ten-class experiments, the method in this paper achieves 97.35% accuracy. The results are better than the experimental results using only LSTM and 1D-SSCNN methods, and the training time is reduced by nearly ten times. The F1 score is used to illustrate the classification accuracy of each class of stellar spectra, and the F1 value of each type is above 0.9 in both the three-classification and ten-class experiments. Compared with the results of previous experiments in the literature, the results of this paper's model are better. With the confusion matrix results, it can be concluded that the model's accuracy in this paper is higher in the experiments with more spectral categories, and it can even reach 100%. In summary, the model based on the combination of CNN and LSTM proposed in this paper can effectively classify large-scale stellar spectral data and achieve excellent classification results.

Keyword: LAMOST; Spectral classification of stars; CNN; LSTM; Z-Score standardization
引言

LAMOST是一项由中国科学院国家天文台运营的中国国家研究设备[1], 其在大规模光学光谱观测和大视场天文学研究方面处于国际领先地位。 该设备不仅具备高效采集光谱数据的能力, 还能够生成科学质量的数据。 截至目前, LAMOST已发布了超过48万个天体光谱, 为研究宇宙的大尺度结构以及星系的结构与演化做出了重要贡献[2]。

摩根· 肯那分类法[3](MK分类法)是分类这些恒星光谱最典型的方法。 它的分类规则是: 按照温度由低到高分为M、 K、 G、 F、 A、 B、 O七大类。 每大类还可以细分成子类, 例如F型光谱可以细分为F0— F9十类子光谱。 每条恒星光谱都是一条曲线, 其横坐标表示波长(Wavelength), 纵坐标表示流量强度(Flux)。 通过观察在波长变化的过程中流量强度的变化, 可以发现不同光谱数据之间的隐含特征。

当前, 天文学家们面临着如何自动、 高效、 准确地分类海量天文光谱数据的问题。 在恒星光谱数据分类研究中, 许多学者采用了传统的方法。 其中, 蔡江辉[4]等使用谓词逻辑的分类规则后处理方法提高了光谱自动分类的效率; Wang[5]等使用受限玻尔兹曼机(RBM)、 基于伪逆学习算法的深度神经网络(PILDNN)以及每条光谱作为输入向量时分为4个阶段并基于PILDNN(PILDNN* )进行分类任务, 结果准确率高, 但需要进行数据降维; 许婷婷[6]等提出了一种深度信念网络对光谱数据进行分层特征学习, 并进行了三分类的任务, 实验表明它在综合性能上优于其他分类算法; Kuntzer[7]等提出了一种有监督的机器学习方法, 基于主成分分析进行降维, 然后由人工神经网络预测光谱类型; Dafonte[8]等提出了一个复杂的混合系统, 包括了人工神经网络、 反向传播算法、 径向基函数等, 可自动收集最重要的光谱特征, 确定恒星的光谱类型; Li[9]等基于17阶多项式拟合对频谱进行归一化, 并利用随机森林对恒星光谱进行分类, 但同样具有数据需要降维的缺点; Liu[10]等使用光谱线指标对光谱进行分类, 但需要高信噪比的数据。

随着深度学习技术的不断发展, 天文学家们能够更加高效地处理海量光谱数据, 实现更快更准确的分类, 为天文学研究提供了有力的支撑。 其中, 卷积神经网络(CNN)在图像分类、 图像识别、 语音识别等领域被广泛应用, 并在特征提取方面具有很强的优势。 由于恒星光谱具有Flux特征, CNN在光谱分类中的应用也开始逐渐出现。

在使用一维CNN方法对光谱进行分类的研究中, Liu等[11]提出了一种基于一维恒星光谱卷积神经网络(1D-SSCNN)的监督算法, 用于提取光谱特征并进行分类。 而何东远等[12]则利用一维卷积神经网络算法对斯隆数字巡天(SDSS)的恒星光谱进行分类, 但他们的模型在训练时间上仍有可能进行优化。 在对光谱进行分类时, 另一种常见的方法是使用二维CNN。 例如, Zhang[13]等利用短时傅里叶变换将一维光谱转化为二维傅里叶谱图像, 并使用卷积神经网络对其进行分类。 尽管这种方法提高了分类精度, 但将数据转化为图像的过程比较耗时。 另外, Lu[14]等提出了基于二维恒星光谱数据分类的方法, 并使用全连接神经网络分类模型, 为恒星光谱的处理提供了新的思路和方法, 但分类精度仍有提升的空间。 Vilavicencio-Arcadia[15]等使用Levenberg-Marquardt优化算法训练前馈神经网络和广义回归神经网络, 并使用这两种方法对二维光谱数据进行分类, 但这种方法对数据的归一化操作非常敏感。 Yoon[16]提出CNN中的全连接层只能捕捉到序列数据中的局部特征而不是全局特征, 这个问题如果可以解决, 将会进一步提高模型的准确率。

在研究过程中发现深度神经网络中还有一类递归神经网络, 包括循环神经网络、 长短期记忆网络(LSTM)、 门控制循环单元等。 这些模型均以序列数据为输入, 通过在序列的演进方向上进行递归操作, 并以链式方式连接所有循环节点来进行计算。 由于这些模型具有记忆性和参数共享的特点, 因此在学习序列数据的非线性特征方面具有很大的优势。 何丽[17]等将深度学习中的LSTM应用到音乐流派分类中。 从包含10种音乐流派的1 000首歌曲频谱中提取特征, 将提取出来的特征数据输入到LSTM网络中进行训练, 输出每种音乐类别的概率, 实验结果表明该方法在准确率上比玻尔兹曼机和卷积神经网络等方法都有所提升。 考虑到我们研究的光谱数据也属于频谱类数据, 采用LSTM网络有助于提取光谱数据中的长距离依赖关系, 从而更深层次地发现每类光谱之间的微小差异。

通过以上论述, 本文提出了一种新的复合深度学习模型, 将LSTM网络重新设计以适应光谱数据, 并与CNN结合, 以完成正确分类光谱数据, 并用于研究宇宙的演化过程、 星系的形成和演化与发现新化学物质等目标。 该模型包括卷积层、 池化层、 长短期记忆层、 全连接层和使用ReLU激活函数的预测结果层, 以及使用Softmax进行光谱数据的分类。 通过卷积层和池化层提取光谱中的特征, 并将其输入到长短期记忆层中进行训练, 以实现更加准确和高效的光谱分类。

1 数据与数据标准化
1.1 恒星光谱数据

本文使用的恒星光谱实验数据来源于LAMOST DR8数据库, 数据详见表1。 第一部分数据包含30 000条F、 G、 K三种类型的恒星光谱数据, 信噪比大于20, 每种类型光谱数据各为10 000条。 第二部分数据则包含20 000条A0、 A5、 F0、 F5、 G0、 G5、 K0、 K5、 M0、 M5十种子类型的恒星光谱数据, 信噪比大于20, 每种子类型光谱数据各为2 000条。 这些恒星光谱数据的波长范围为370~910 nm。

表1 选自LAMOST DR8的实验数据集 Table 1 Selected from the experimental data set of LAMOST DR8
1.2 光谱数据预处理标准化方法

从LAMOST DR8中获取的每条光谱数据都带有对应的唯一标识obsid。 例如本文中选取的obsid为210 209和101 064, 它们的光谱如图1上侧所示。 我们可以观察到不同恒星光谱的流量强度数值差异很大, 这个因素在使用深度神经网络模型学习光谱特征时可能会产生很大的影响。 为了消除不同光谱的流量强度数值大小相差很大的影响, 我们需要对数据进行归一化或标准化处理。 将数据标准化可以使模型梯度下降更快, 因为它可以使数据分布更加均匀, 避免不同特征之间数值差异过大导致的偏差和不稳定性。 标准化后, 所有特征的取值范围相似, 有利于模型更快地收敛, 并减小特征之间的差异性, 有助于避免模型的过拟合问题。 因此本文引入了Z-Score标准化(zero-mean normalization)方法, 如式(1)

Ss=SN-μσ(1)

式(1)中, SN=(S1, S2, …, Sn)表示原始恒星光谱数据, S1, S2, …, Sn表示给定波长下的流量强度值, Ss表示归一化后的恒星光谱数据, μ 表示SN中的流量强度值的平均值, σ 表示SN中的流量强度值的标准差。

我们将上述取得的obsid为210 209、 101 064的恒星光谱数据进行Z-Score标准化, 标准化后的光谱数据如图1下侧图像, 可以看出标准化后的光谱数据与原数据具有相同的尺度和变异程度, 并仍然保持了原始光谱数据特征之间的相对大小关系。

图1 标准化前的恒星光谱图像(上), 标准化后的恒星光谱图像(下)Fig.1 Spectral images of stars before standardization (top) and after standardization (bottom)

2 CNN与LSTM复合深度模型的设计
2.1 CNN

CNN是深度学习模型中最典型的一种。 通常包含输入层、 卷积层、 激活函数、 最大池化层、 全连接层和输出层。 其中一维卷积神经网络(1D-CNN)适用于处理一维序列数据, 因为它可以通过卷积操作捕捉到序列数据中的局部特征, 同时保留了原始序列的顺序。 1D-CNN可以使用一维卷积核对序列数据进行卷积操作, 从而在每个时间步上捕捉到局部特征, 通过在不同时间步上进行最大池化操作并对结果进行汇合, 1D-CNN可以逐渐捕捉到序列数据中的全局特征, 这非常适用于光谱数据特征的分析与挖掘。 全连接层则将提取的特征进行矩阵向量乘积, 以便于后续输出层的分类操作。 然而, 当前的1D-CNN模型中全连接层在处理序列数据时只能考虑当前时间步的特征, 而无法考虑之前的历史信息, 而且在反向传播时容易产生梯度消失的问题, 这会导致模型的训练困难, 对于这些问题长短期记忆细胞结构恰好可以解决此问题。

2.2 LSTM

长短时记忆网络(LSTM)网络模型设计了三个门, 分别是输入门、 遗忘门和输出门。 通过这三个“ 门” 的控制, LSTM可以很好地保护和控制网络中的细胞状态。 LSTM可以通过门控机制, 有效地捕捉到序列数据中的长期依赖关系, 从而提高模型的准确性, 还可以帮助网络有效地控制梯度的流动, 从而减轻梯度消失问题的影响。 图2展示了LSTM的内部结构, 通过设计的独特门控机制, 可以灵活地决定哪些信息需要被遗忘、 哪些信息需要被保留。

图2 长短期记忆细胞结构Fig.2 Cell structure of LSTM

输入门用来决定细胞中应该加入哪些新状态。 此项设计两部分工作: 第一部分是通过使用输入门的sigmoid层决定我们要去更新哪些位置上的值, 第二部分是通过tanh层生成一个候选值组成可加到细胞状态上的向量。 输入门状态更新公式

it=σ(Wi[ht-1, xt]+bi)(2)

C˙t=tanh⁡tanhWcht-1, xt+bc(3)

式(2)和式(3)中, σ (· )表示sigmoid函数, [ht-1, xt]表示上一时刻LSTM的输出值ht-1与当前时刻LSTM的输入值xt组成的向量, it表示输入门的输出, Wi表示输入门的权重矩阵, bi表示输入门的偏置。 C˙t表示当前时刻的单元状态, Wc表示输入单元的权重, bc表示输入单元的偏置。

遗忘门是sigmoid层综合前一时刻的隐藏状态和当前时刻的输入数据做出是否让这些信息通过的决定。 “ 0” 表示完全忘记, “ 1” 表示完全保留。 遗忘门状态更新公式

ft=σWfht-1, xt+bf(4)

式(4)中, ft为遗忘门的输出, Wf表示遗忘门的权重矩阵, bf为遗忘门的偏置。

输出门是基于当前的细胞状态, 首先通过一个tanh层来把细胞状态映射到区间(-1, 1)内, 接着, 利用输出门的sigmoid层控制输出细胞状态中的信息。 输出门状态更新公式

ot=σWoht-1, xt+bo(5)

式(5)中, ot表示当前输出门的输出, W0表示输出门的权重矩阵, bo表示输出门的偏置。

更新细胞Ct细胞状态

Ct=ft* Ct-1+it* C˙t(6)

式(6)中, * 表示哈达玛积。

输出

ht=ot* tanh(Ct)(7)

2.3 CNN与LSTM复合深度模型

在LAMOST光谱分类工作中, 以F、 G、 K三类恒星为代表的谱型分类系统非常实用。 这些恒星具有适中的光度, 化学成分差异大, 是行星搜索中最有希望发现地外行星的恒星类型。 利用它们的光谱特征可以研究恒星的化学成分、 演化过程和形成, 进而推动对宇宙演化过程的理解。 除了以F、 G、 K三类恒星为代表外, 在LAMOST恒星光谱分类工作中还会使用更具体的谱型分类, 如A0、 A5、 F0、 F5、 G0、 G5、 K0、 K5、 M0、 M5。 因为不同谱型具有不同的光谱特征, 可以反映出恒星的物理性质、 化学成分、 演化状态等信息, 在研究恒星时, 这些信息对于理解宇宙演化过程至关重要。 所以本文将从恒星光谱的三分类任务与恒星光谱十分类任务, 两个方面进行本文模型的设计。

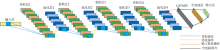
在1D-CNN模型中的全连接层无法有效利用历史信息, 只能考虑当前时间步特征。 相比之下, LSTM模型通过特有的“ 门” 可以更好地捕获序列数据中的长期依赖关系, 从而提高模型的准确性。 由此本文提出CNN与LSTM复合深度网络结构其形状如表2所示, 具体结构如图3所示。 模型的输入层长度为3 700* 1的光谱数据, 第一个卷积层使用15* 1的卷积核尺寸和20个滤波器, 激活函数为Relu; 第一个最大池化层使用卷积核尺寸为5* 1, 滤波器个数为20个。 第二个和第三个卷积层、 最大池化层的配置与第一个卷积层、 池化层相同。 第四个卷积层使用6* 1的卷积核尺寸和15个滤波器, 激活函数为Relu; 第四个最大池化层使用卷积核尺寸为3* 1, 滤波器个数为15个。 紧接着后面是一个LSTM层, 其输出大小为128, 激活函数为tanh, 为防止过拟合, 接了一个Dropout函数, 配置为0.3。 随后是一个包含1 024个神经元的全连接层, 激活函数为Relu, 同样涉及一个Dropout函数, 配置为0.3。 最后的输出层设置为3个或10个神经元, 用于表示三分类任务或十分类任务中光谱类别的概率, 再通过Softmax函数将多分类的输出值转换为[0, 1]范围内的概率。

表2 CNN与LSTM复合网络结构 Table 2 CNN and LSTM composite network structure

图3 CNN与LSTM复合网络结构Fig.3 CNN and LSTM composite network structure

3 实验设计与结果对比
3.1 光谱三分类实验设计、结果与对比

为了验证本文所提出的基于CNN与LSTM复合深度模型相较传统的DBN[6]、 Inception v3[13]、 PILDNN[5]、 PILDNN* [5]、 RBM[5]网络的有效性, 实验采用与DBN与和Inception v3模型训练的相同数量数据集, 即30 000条恒星光谱数据, 作为样本数据, 进行接下来本文模型训练与测试, 并将实验结果与它们进行比较。 尽管文献[5]中PILDNN、 PILDNN* 、 RBM网络训练中使用的数据量更大, 即50000条恒星光谱数据, 但由于本文使用的数据集也来自LAMOST数据库, 且仅包含F、 G和K型恒星光谱数据, 因此不会对实验结果对比产生影响。 相反, 使用较少的数据量训练出效果更好的模型进一步说明了本文提出的模型的有效性。 为了说明将CNN与LSTM复合深度模型相较单一的CNN模型、 LSTM网络的优势, 本文将文献[11]中仅由传统CNN构成的1D-SSCNN模型, 以及本文模型去除卷积层和池化层仅采用LSTM网络构成的模型在本文的数据集上进行了实验并进行实验结果对比, 以说明本文提出的复合深度模型的有效性。 下面将进行本文三分类模型的实验。

为了训练本文中的三分类模型, 我们使用1.1节中设计的第一部分数据集, 并设置学习率为0.001, 训练次数为50次, 批处理个数为128。 训练集包括24 000条恒星光谱数据, 验证集包括3 000条恒星光谱数据, 测试集包括3 000条恒星光谱数据, 使用2.3节中输出层取3个神经元来代表三类光谱的分类概率。 图4展示了不同迭代次数下验证集分类准确率的变化情况。 从图中可以看出, 随着训练次数的增加, 验证集的分类准确率也随之上升。 最初的准确率增长速度很快, 而后逐渐趋于平缓, 最终稳定在92%以上。 我们将测试集数据用模型进行预测, 并将预测结果与真实的恒星光谱类别进行对比, 发现本文模型的准确率高达94.56%。

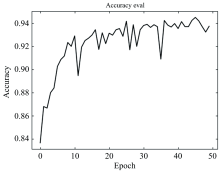图4 F、 G、 K三大类恒星光谱验证集在模型上的准确率
与前人实验准确率与模型训练时间对比结果见表3, 可见本文提出的复合深度模型在数据预测方面相较传统的RBM、 PILDNN、 PILDNN* 、 Inception v3、 DBN网络的实验结果具有更高准确率, 说明本文提出的复合深度模型是有效的。 同样, 相较于单一的1-D SSCNN与单一的LSTM网络的实验结果也具有更高准确率, 说明本文复合后的深度模型在光谱分类实验是更加有效的。 在训练所消耗的时间方面, 可以在表中看到本文算法也是相当有效率的。Fig.4 The accuracy of the three categories of stellar spectra F, G and K are verified in the model

表3 与文献[5, 6, 11, 13]分类结果对比 Table 3 Compared with the classification results of literatures [5, 6, 11, 13]

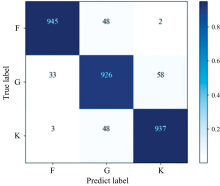
为了更加说明本文提出方法的优势, 我们引入了统计学中混淆矩阵的方法以及F1-score方法进行评价本文设计的模型。 混淆矩阵就是分别统计分类模型归错类, 归对类的观测值个数, 然后把结果放在一个矩阵里展示出来的矩阵称为混淆矩阵。 F1-score方法是同时兼顾模型的查准率和召回率的一种衡量指标。 它的最大值为1, 最小值为0。 值越大, 说明分类的效果越好。 F1-score的计算公式为

F1=2PRP+R(8)

P=TPTP+FP(9)

R=TPTP+FN(10)

式(8)— 式(10)中, P表示查准率, R表示召回率, TP表示预测答案正确数量, FP表示错误将其他类预测为本类数量, FN表示本类预测为其他类数量。

鉴于训练DBN与和Inception v3模型的参考文献中未提供F1-score的实验结果, 本文将与RBM、 PILDNN、 PILDNN* 、 1-D SSCNN以及LSTM的F1-score进行对比, 结果呈现在表4中。 从表中可以看出, 本文提出的模型在每个光谱分类中的F1值更高, 能够强有力的说明本文模型准确地对光谱类型进行分类。 同时, 通过观察图5中本文三分类模型预测结果的混淆矩阵, 可以发现归类错误的数量极少。 因此, 本文提出的模型在光谱分类方面具有显著优势, 能够实现高准确度的分类预测。

表4 三分类F1-score的结果对比 Table 4 Three categories of F1-score comparison of results

图5 F、 G、 K类型光谱分类混淆矩阵Fig.5 Spectral classification confusion matrix of F, G and K types

3.2 光谱十分类实验设计、 结果与对比

正如3.1节所述, 为了说明将CNN与LSTM复合深度模型相较单一的CNN模型、 LSTM网络的优势, 本文将文献[11]中仅由传统CNN构成的1D-SCNN模型, 以及本文模型去除卷积层和池化层仅采用LSTM网络构成的模型在本文的数据集上进行了实验并进行实验结果对比, 以说明本文提出的复合深度模型的有效性。 下面将进行本文十分类模型的实验。

本文的十分类模型训练使用了1.1节中设计的第二部分数据集, 学习率为0.001, 训练次数为50次, 批处理大小为128, 其中训练集包括16 000条恒星光谱数据, 验证集包括2 000条恒星光谱数据, 测试集包括2 000条恒星光谱数据。 使用2.3节中输出层取10个神经元的网络, 代表十类光谱的分类概率。 在不同迭代次数下, 验证集的分类准确率随着模型训练次数的增加而上升, 如图6所示。 图中显示, 初始训练后, 验证集的准确率快速增长, 然后趋于平缓, 并最终稳定在94%以上。 在模型中使用测试集数据进行预测, 并将其与真实的恒星光谱类别进行比较, 发现分类结果的准确率高达97.35%。

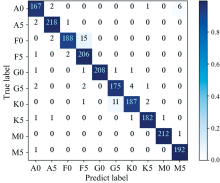
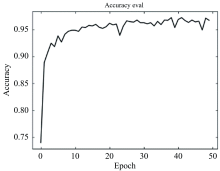图6 A0、 A5、 F0、 F5、 G0、 G5、 K0、 K5、 M0、 M5十种子类恒星光谱验证集在模型上的准确率
通过对比表5中的结果, 可以发现本文提出的模型相比于单一传统的CNN和单一的LSTM网络, 在实验结果中获得更高的准确率。 同时可以看到本文模型能够在训练时间极少的情况下实现高准确度的预测。 通过观察表6, 我们可以看出本文所提出的模型相比于单一传统的CNN和单一的LSTM网络, 在绝大多数光谱类别中获得的F1值更高。 同时, 通过观察图7中本文十分类模型预测结果的混淆矩阵, 可以发现归类错误的数量极少, 数量几乎可以忽略不计。Fig.6 A0, A5, F0, F5, G0, G5, K0, K5, M0, M50 ten stellar spectra verify the accuracy of the set in the model

表5 与文献[11]分类结果对比 Table 5 Compared with the classification results of literature [11]
表6 十分类F1-score的结果对比 Table 6 Ten categories F1-score comparison of results

图7 A0、 A5、 F0、 F5、 G0、 G5、 K0、 K5、 M0、 M5十种子类型分类混淆矩阵Fig.7 A0, A5, F0, F5, G0, G5, K0, K5, M0, M50 ten seed type classification confusion matrix

4 结论

LAMOST恒星光谱数据中蕴涵大量的光谱信息, 可用于研究银河系结构、 化学成分等, 随着技术的不断进步, 它将会继续为天文学研究提供越来越多的重要数据, 快速正确的分类光谱数据可以进一步研究宇宙的演化过程、 星系的形成和演化。 在处理序列数据时, 传统的1D-CNN模型中的全连接层只能考虑当前时间步的特征, 无法考虑历史信息, 并容易产生梯度消失问题。 相比之下, LSTM模型可以通过门控机制有效地捕捉序列数据中的长期依赖关系, 提高模型准确性, 同时也可以帮助网络控制梯度流动, 减轻梯度消失问题的影响, 因此本文提出了一种基于CNN与LSTM复合深度模型的恒星光谱分类算法。 通过与PILDNN、 PILDNN* 、 RBM、 Inception v3、 DBN、 LSTM、 1D-SSCNN等算法的实验结果进行对比, 本文方法在三分类和十分类实验中均取得了更高的准确率, 同时训练时间也更短。 为了说明本文方法的优势, 本文引入了F1-Score进行实验结果对比, 结果表明本文方法在光谱三分类和十分类结果的F1值更高。 混淆矩阵结果也表明, 本文对数据的分类正确程度效果也较好。 本文提出的分类方法可以显著提高光谱分类的效率和准确性, 节省时间和成本。 对于研究恒星的物理性质、 化学成分和演化状态等重要信息, 可以更快地提供大量数据, 进而提高恒星研究的效率和准确性。 并且可以在获取有关恒星物理特性和演化历程信息的工作中速度更快, 进而为相关领域的研究和应用提供更多的数据支持。

参考文献
[1] Zhao G, Zhao Y H, Chu Y Q, et al. Research in Astronomy and Astrophysics, 2012, 12(7): 723. [本文引用:1]
[2] Cui X Q, Zhao Y H, Chu Y Q, et al. Research in Astronomy and Astrophysics, 2012, 12(9): 1197. [本文引用:1]
[3] Kheirdastan S, Bazarghan M. Astrophysics and Space Science, 2016, 361: 304. [本文引用:1]
[4] CAI Jiang-hui, YANG Hai-feng, ZHAO Xu-jun, et al(蔡江辉, 杨海峰, 赵旭俊, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2013, 33(1): 237. [本文引用:1]
[5] Wang K, Guo P, Luo A L. Monthly Notices of the Royal Astronomical Society, 2017, 465(4): 4311. [本文引用:5]
[6] XU Ting-ting, MA Chen-ye, ZHANG Jing-min, et al(许婷婷, 马晨晔, 张静敏, 等). Acta Astronomica Sinica(天文学报), 2019, 60(2): 15. [本文引用:2]
[7] Kuntzer T, Tewes M, Courbin F. Astronomy & Astrophysics, 2016, 591: A54. [本文引用:1]
[8] Dafonte C, Rodríguez A, Manteiga M, et al. Entropy, 2020, 22(5): 518. [本文引用:1]
[9] Li X R, Lin Y T, Qiu K B. Research in Astronomy and Astrophysics, 2019, 19(8): 111. [本文引用:1]
[10] Liu C, Cui W Y, Zhang B, et al. Research in Astronomy and Astrophysics, 2015, 15(8): 1137. [本文引用:1]
[11] Liu W, Zhu M, Dai C, et al. Monthly Notices of the Royal Astronomical Society, 2019, 483(4): 4774. [本文引用:3]
[12] HE Dong-yuan, LIU Wei, CAO Shuo, et al(何东远, 刘伟, 曹硕, 等). Journal of Beijing Normal University(Natural Science Edition) [北京师范大学学报(自然科学版)], 2020, 56(1): 37. [本文引用:1]
[13] Zhang J M, Ma C Y, Wang L, et al. Chinese Astronomy and Astrophysics, 2020, 44(3): 334. [本文引用:2]
[14] Lu Y, Qiu B, Xiang G, et al. Journal of Physics: Conference Series. IOP Publishing, 2020, 1626(1): 012016. [本文引用:1]
[15] Vilavicencio-Arcadia E, Navarro S G, Corral L J, et al. Mathematical Problems in Engineering, 2020, 2020: 1751932. [本文引用:1]
[16] Yoon K. Conference on Empirical Methods in Natural Language Processing , 2014. [本文引用:1]
[17] HE Li, YUAN Bin(何丽, 袁斌). Computer Technology and Development(计算机技术与发展), 2019, 29(11): 190. [本文引用:1]