一种两阶段求解LED光谱匹配系数高效全局优化算法

引用本文

王永军, 吴贵文, 黄河, 李同军. 一种两阶段求解LED光谱匹配系数高效全局优化算法[J]. 光谱学与光谱分析, 2024,44(6): 1591-1599.
WANG Yong-jun, WU Gui-wen, HUANG He, LI Tong-jun. A Two-Stage Efficient Global Optimization Algorithm for Solving LED Spectral Matching Coefficient[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1591-1599.
Doi:10.3964/j.issn.1000-0593(2024)06-1591-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

一种两阶段求解LED光谱匹配系数高效全局优化算法

王永军¹, 吴贵文^2,^*, 黄河¹, 李同军³

1. 温州职业技术学院人工智能学院, 浙江温州 325035

2. 温州商学院信息工程学院, 浙江温州 325035

3. 浙江海洋大学信息工程学院, 浙江舟山 316022

*通讯作者 e-mail: 302908829@qq.com

作者简介: 王永军, 1970年生, 温州职业技术学院人工智能学院博士(后) e-mail: wangyjmcvti@qq.com

收稿日期: 2023-02-23 修回日期: 2023-10-12

基金: 温州市重大科技创新攻关项目(ZG2022012)和国家自然科学基金面上项目(61773349)资助

摘要

用单色发光二极管(LED)组份合成目标光谱在现实中有重要意义。当单色LED组成成份多、目标光谱合成精度要求高时, 求解光谱组成成份的比例问题变成了超定方程组非负解的组合优化难题。智能优化类算法提高了解的全局最优性, 但若没有利用目标函数的数学解析性质, 其收敛速度慢, 解的精度不高。梯度类算法收敛到局部解的速度快且精度高, 但至今没有成熟理论技术求解非凸优化全局最优解, 且问题中非负解的要求限制了该类算法的收敛速度。同时, 目标函数的最小二乘信息在求解时没有得到充分利用。基于目标函数的数学可解析性、表现形式的二次非线性格式、最终解的非负要求, 提出了一种两阶段优化算法LLR_LBFGS。第一阶段进行无约束的线性拟合, 得到目标函数的最小二乘近似理论解, 第二阶段借助带约束的拟牛顿方法LBFGS进一步求取问题的非负全局最优解。以标准目标光谱CIE-A、 CIE-D65、 CIE-D50、 CIE-D55、 CIE-D75的最佳拟合为研究对象, 对比了新方法与拉索回归算法(LASSO)、岭回归算法(RIDGE)、差分进化算法(DE)、粒子群算法(PSO)及遗传算法(GA)的求解精度和运行速度, 以及决策系数 R²。基于实际工业案例的数值结果表明, LLR_LBFGS能够较快地锁定全局解的范围, 收敛速度更快; 能够借助目标函数的数学可解析性提高解的精度。两个阶段的衔接融合能够获得较好的全局最优解的起始点和高精度的最优解。该方法对解决LED光谱拟合问题潜力大, 有普适性。基于该设计思路, 可以在算法的两个阶段中, 组合设计更多、更灵活的光谱配比解决方案。这对于求取LED光谱匹配最优解的智能优化类方法改善效果有较好的启发意义。

关键词: 光谱学; LED光谱匹配; 线性拟合; LBFGS; 高效; 全局优化

中图分类号:O433.4 文献标志码:A

A Two-Stage Efficient Global Optimization Algorithm for Solving LED Spectral Matching Coefficient

WANG Yong-jun¹, WU Gui-wen^2,^*, HUANG He¹, LI Tong-jun³

1. School of Artificial Intelligence, Wenzhou Polytechnic, Wenzhou 325035, China

2. School of Information and Engineering, Wenzhou Business College, Wenzhou 325035, China

3. School of Information and Engineering, Zhejiang Ocean University, Zhoushan 316022, China

*Corresponding author

Abstract

The synthesis of the required target spectrum with monochromatic light-emitting diodes (LED) is of great significance in reality. When multiple components of the LEDs are needed, and the accuracy required for the target spectrum synthesis is high, solving the problem of the proportion of the components becomes a combination optimization problem with a non-negative solution of the over-determined set of linear equations. Generally speaking, the approximately global solutions can be found for the heuristic-based methods. However, the convergence speed to the worldwide optimizer is low partly because the objective functions' analysis properties, such as gradient information, are not used. Gradient-based algorithms converge to local solutions fast and with high accuracy, but the requirement for non-negative solutions in the problem limits their global convergence. Meanwhile, the least squares information of the objective function was not fully utilized in previous research. In this paper, a two-stage optimization algorithm, named LLR_LBFGS, is proposed based on the mathematical analytic properties, the quadratic nonlinear format of the objective function, and the non-negative requirements for the final solution. In the first stage, unconstrained linear fitting is carried out to obtain the unique solution of the least squares theory of the expressions. In the second stage, the non-negative global optimal solution of the problem is further obtained with the help of the constrained quasi-Newtonian method LBFGS. Taking the fitting of standard target spectra CIE-A, CIE-D65, CIE-D50, CIE-D55 and CIE-D75 as the research object, the new method is compared with the Lasso Regression Algorithm (LASSO), Ridge Regression Algorithm (RIDGE), Differential Evolution Algorithm (DE), Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) in solving the same problem in terms of accuracy, running speed, and the decision coefficient R². The numerical results based on actual industrial cases show that the LLR_LBFGS converge faster, and the solution accuracy is higher because the information on the objective function is utilized more efficiently. Its universality indicates excellent potential to be applied more generally to solve the problem of LED spectral fitting. A more flexible solution to solve the spectral matching problem can be set up according to the design ideas of this paper. This also has significant implications for improving the effectiveness of intelligent optimization methods for finding the optimal solution for LED spectral matching.

Keyword: Spectroscopy; LED spectral matching; Linear fitting; LBFGS; High effectiveness; Global optimization

文章图片

引言

标准光源是指模拟各种环境光线的人造光源, 其作用是让生产工厂或实验室在非现场也能获得与这些特定环境下的光源基本一致的照明效果。通过使用LED作为光源配比生成的不同标准光源, 已经广泛地应用于纺织印染、印刷、油漆、造纸、食品、植物保护和设施农业等行业^{[1, 2, 3]}。

国际照明委员会CIE规定了一些标准照明体的相对光谱功率分布^[4]。现有的标准光源都是用某种灯具模拟产生相应的光谱曲线, 只要其色温在误差范围以内且发光强度亦满足要求即可。以卤钨灯加滤光片模拟某些标准光源, 功率大且发热明显, 灯丝易断, 寿命短。以特制荧光灯模拟某些标准光源, 其混合光谱与标准光谱功率分布差别较大, 光能衰减快使用寿命短。随着半导体技术的发展, 作为第四代照明光源的LED有发光效率高、使用寿命长、性能稳定、波长种类丰富、单色性好、半峰全宽(FWHM)窄的优点和发光光谱等特性能较好地控制^[2], 且这些特性可以组合不同波段LED模拟产生连续分布的目标光谱^[5]。作为一种新型的冷光源 , LED还有很多传统光源所不能比拟的优势, 例如: 灯源单元面较小, 不需要充气体, 不需要玻璃外壳, 抗冲击性能好, 便于运输, 能够较好地控制发光光谱组成等。因此LED照明已经得到广泛使用, 研究采用LED灯实现标准光源具有重要意义。

沈海平等开展了LED光谱数学模型创建研究为光谱合成和理论研究奠定了基础^[6]。为了探索如何控制各个LED才能达到更好的拟合度, 研究者开发了一些拟合算法。比如甘汝婷等在利用单色LED实现CIE-D65标准光源、 AM1.5标准太阳光的匹配时, 提出了简单遗传算法作为光谱匹配方法, 通过求解超定方程组的非负最小二乘解, 优化不同峰值波长、峰值波长间隔、半高宽的单色LED匹配光源组合, 达到光源光谱匹配的目的^[7]。郭震宁等优化了单色发光二极管(LED)匹配光源组合, 实现用白光LED取代部分单色LED模拟太阳光谱^[8]。程真设计了改进的差分进化算法(DE)解决实验室目标光谱数据的匹配优化问题, 取得了较好的效果^[5]。张译文等以最小二乘法和高斯分布数学模型为基础, 理论上实现了非均匀间隔峰值波长的光谱拟合, 从而指导LED的种类选择及其所需的驱动电流值, 并通过实验论证了其可行性^[9]。汤露瑶等选用了三种不同色温下的太阳光谱作为目标拟合光谱, 借助Matlab优化工具箱中的fmincon 函数求解了不同目标光谱下各组LED的功率组合系数^[10]。高源等运用线性规划方法对各通道LED配比进行优化, 实现了LED混光光源的目标光谱^[11]。倪俊雄等采用最小二乘法成功拟合出几种特征明显的常见标准光源光谱^[12]。高航采用改进的遗传算法与神经网络结合设计了求取光谱配比系数方法, 取得了一定的效果^[13]。实际上, 非凸优化问题的全局最优解问题在理论上至今没有解决。现实中的许多全局优化问题仍是挑战, 需要设计相应的方法策略。如本文的二次规划非负解要求, 破坏了最小二乘法理论解条件, 使得问题变得复杂。随机类启发式方法^[14](比如遗传算法、粒子群方法、差分算法和模拟退火算法等)求解这类问题速度慢, 精度低。如能充分利用目标函数的数学分析性质设计全局优化算法, 在提高收敛速度的同时, 也提高解的精度, 这样的方法是值得开发探索的。

基于上述思想, 设计了两阶段求解目标光谱匹配的LED比例系数全局优化方法。该方法借助于最小二乘通用理论解作为解决问题的初始点(由于非负解的要求, 该理论解不一定符合实际要求), 然后利用梯度优化方法LBFGS^[15]求取局部最优解的精度高和收敛速度快的优势获得最佳配比比例。基于典型标准目标光谱拟合, 与经典算法的比较发现, 提出的方法简单、有效, 在实际工程应用中具有较好的推广价值。

1 目标光谱匹配原理

1.1 单色LED光谱曲线

基于高斯分布函数的单色LED光谱曲线模型见式(1)^[6], 单个LED在光轴方向上的辐射强度为

$\begin{array}{l} s (λ) |_{P, λ_{0}, Δ λ} = \\ P \exp [- 3.2213 {(\frac{λ - λ_{0}}{Δ λ})}^{2} \exp (- 0.3 |\frac{λ - λ_{0}}{Δ λ}|)] \end{array}$ (1)

式(1)中, P是辐射功率峰值, λ 是LED波长, λ ₀是LED波峰波长, Δ λ 是半宽高。不同的单色LED光谱的P、 λ ₀、 Δ λ 不完全相同。

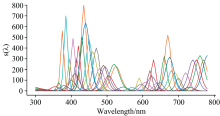
从式(1)可以看出LED光谱是一个典型的类似高斯密度函数的窄带单峰谱线, 沿着光轴λ 的方向, 在单位立体角内随波长的分布呈高斯分布状。根据作者收集的实际LED工业应用数据数值, Δ λ 值在10~30 nm之间, λ ₀值在310~780 nm之间。本工作用到的48种单色LED光谱曲线如图1所示, 从图中可以看到不同LED光谱有不同的波峰波长λ ₀, 即波峰位置不同, 而不同波峰处的Δ λ 值不同。在累加拟合目标光谱时, 与目标光谱波峰相近的λ ₀处对应的单色LED光谱曲线贡献的比例系数可能偏大。本工作的目标就是综合累加单色光谱拟合逼近目标光谱。

	Figure Option View Download New Window
	图1 不同参数的单色LED光谱曲线(不同的P、 λ ₀、 Δ λ )Fig.1 Spectra curve of single LED with different parameters (different P, λ ₀, Δ λ )

1.2 目标光谱匹配原理

应用于某种特定需求的光源发出的光是由不同颜色的波长的光按照比例要求组合成的混合光。混合光中不同波长的单色光的强度不同, 最终线性累加得到的混合光源是不同的。比如, 太阳光谱就是将不同峰值波长的LED光谱按照特征的电流比例(占空比)或数量组合起来的混合光谱。因此, 目标光谱匹配就是给定需要拟合的某种标准(样本)光谱, 选择比例系数不同的LED单色光谱, 使得线性累加后的混合光谱尽量与标准光谱一致^{[5, 7, 8, 9, 10, 11, 12]}。

假设y(λ )是需要拟合的目标光谱, s_i(λ )=s(λ ) $|_{p, λ_{0}, Δ λ}$ [见式(1)]是某一种单色LED光谱, 则宽波段目标光谱拟合可以表达为

$y (λ) = \overset{m}{\sum_{i = 1}} w_{i} s_{i} (λ)$ (2)

式(2)中, m是单色LED光谱个数, w_i是比例系数, λ 是波长。严格来说y(λ )是连续函数, 但是由于光谱仪测量值是某些特定波长的离散性, λ 一般取离散的特定波长λ _j, j=1, 2, …, n(n是离散波长的个数)。那么式(2)可以写成式(3)

$y (λ_{j}) = \overset{m}{\sum_{i = 1}} w_{i} s_{i} (λ_{j}), j = 1, 2, \dots, n$ (3)

式(3)写成矩阵形式[式(4)]

$[\begin{array}{l} s_{1} (λ_{1}) & s_{2} (λ_{1}) & \dots & s_{m} (λ_{1}) \\ s_{1} (λ_{2}) & s_{2} (λ_{2}) & \dots & s_{m} (λ_{2}) \\ \dots & \dots & \dots & \dots \\ s_{1} (λ_{n}) & s_{2} (λ_{n}) & \dots & s_{m} (λ_{n}) \end{array}] [\begin{array}{l} w_{1} \\ w_{2} \\ \dots \\ w_{m} \end{array}] = [\begin{array}{l} y (λ_{1}) \\ y (λ_{2}) \\ \dots \\ y (λ_{n}) \end{array}]$ (4)

若记单色LED光谱数据矩阵A=$\lfloor$s_i(λ _j) $\rfloor$_n_×_m[式(4)的最左端矩阵], W=[w₁, w₂, …, w_m]^T[式(4)的左端第2个列向量], Y=[y(λ ₁), y(λ ₂), …, y(λ _n)]^T[式(4)的右端列向量], 则式(4)可以表达为

$AW = Y$ (5)

根据式(5), 目标光谱的匹配问题就是已知系数矩阵A和标准光谱Y, 求解m个未知数w_i, 使得n个方程 $y (λ_{j}) = \overset{m}{\sum_{i = 1}} w_{i} s_{i} (λ_{j})$ 组成的线性方程组成立。显然, 目标匹配问题也可以看成输入样本$\lfloor$s₁(λ _j), s₂(λ _j), …, s_m(λ _j)$\rfloor$, y(λ _j), 其中$\lfloor$s₁(λ _j), s₂(λ _j), …, s_m(λ _j) $\rfloor$, y(λ _j)分别为数据和标签的无截距的线性拟合问题y(λ )=w₁s₁(λ )+w₂s₂(λ )+…+w_ms_m(λ ), λ =λ ₁, λ ₂, …, λ _n, w₁, w₂, …, w_m为拟合系数。

当n> m时(现实中往往是这样的情况), 线性方程组[式(5)]变成了超定线性方程组。根据线性方程组的数学解的性质, 线性方程组(5)一般无解。这时, 可以转化为求解最小二乘意义下线性方程组的广义解, 也就是求解残差‖ AW-Y‖ ₂在2范数意义下的极小值解。

$W^{*} = \arg (‖ A W^{*} - Y_{2}) = \arg (\min_{w} ‖ AW - Y ‖_{2})$ (6)

从理论上讲, 式(6)有最小二乘意义下的唯一解[式(7)]

$\boldsymbol{W}^{*}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{Y}$ (7)

但是, 由于实际要求, 比如要求解向量的各个分量为非负时, 式(7)的结果不一定符合约束条件, 这时, 问题变得复杂, 需要改造常规算法或设计新的算法。

1.3 评价指标

根据线性回归或线性拟合中, 衡量拟合效果的均方根误差大小的直接指标为式(8)^[5]

$\begin{array}{c} \text { RMSE }=\sqrt{\frac{1}{n}\|\boldsymbol{A} \boldsymbol{W}-\boldsymbol{Y}\|_{2}}= \\ \sqrt{\frac{1}{n} \sum_{j=1}^{n} \sum_{i=1}^{m}\left(\left|w_{i} s_{i}\left(\lambda_{j}\right)-y\left(\lambda_{j}\right)\right|\right)^{2}} \end{array}$ (8)

RMSE越接近于0, 则拟合效果越好。

通过衡量拟合曲线与标准数据的相似程度的评价光谱匹配度指标见式(9)^[5]

$\begin{array}{c} R^{2}=1-\sum_{j=1}^{n} \sum_{i=1}^{m}\left[w_{i} s_{i}\left(\lambda_{j}\right)-y\left(\lambda_{j}\right)\right]^{2} / \\ \sum_{j=1}^{n} \sum_{i=1}^{m}\left[y\left(\lambda_{j}\right)-\bar{y}(\lambda)\right]^{2} \end{array}$ (9)

式(9)中, $\overset{̅}{y}$ (λ )是y(λ _j)(j=1, 2, …, n)的数学期望。 R²表达了拟合曲线与原始数据的相似程度, R²值越接近1表明拟合效果越好, 相应的解的精度越高。

另外, 在保证求解精度的条件下, 求解速度有时也是考察算法的检验指标。

2 两阶段光谱匹配算法

分析本工作的拟合目标光谱任务[式(6)]发现, 目标函数有较好的数学分析性质, 比如求解的问题属于二次规划优化问题、目标函数有导数等。这时, 有一些传统的方法可以参考。这样的目标函数, 如果单纯采用随机算法, 比如SA、 GA、 PSO和DE等优化算法求解问题, 而不考虑目标函数的分析特性, 经验和实验表明求解的速度和精度往往会慢和低一些。而利用目标函数分析性质的梯度类优化方法, 如最速下降法、牛顿法、拟牛顿法等求取局部最优值速度会更快、解的精度高, 但是这些方法的最终解的质量常常依赖于初始点。对于存在多个局部最优点的非凸函数, 这些方法往往只能得到局部最优解。即使对于式(6), 因为问题中非负解的约束条件, 采用最小二乘理论解[式(7)]得到的结果往往不符合要求。因此, 既能利用目标函数的分析性质, 又保证求得的解符合实际要求, 且收敛速度快、精度高的算法是本工作探索的目标。

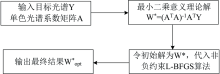
利用目标函数的分析性质, 首先求得式(6)的最小二乘意义下最优解[式(7)], 以式(7)的解为初始点, 设计带约束的拟牛顿法BFGS优化算法^[15]求解问题非负解。其算法见LLR-LBFGS方法, 算法流程见图2。

	Figure Option View Download New Window
	图2 两阶段LLR-LBFGS算法流程Fig.2 The flow chart of two-stage LLR-LBFGS algorithm

LLR-LBFGS算法步骤如下:

(1)输入目标光谱数据Y=[y(λ ₁), y(λ ₂), …, y(λ _n)]^T和单色LED光谱矩阵A=$\lfloor$s_i(λ _j) $\rfloor$_n_×_m;

(2)求解最小二乘意义下的AW=Y的最优解W^*=(A^TA)^-1A^TY;

(3)以W^*为初始解, 使用约束LBFGS算法(见下面LBFGS算法步骤)求解AW=Y的非负最优解。

其中, LBFGS算法是由Broyden、 Fletcher、 Goldfarb和Shanno四人提出的拟牛顿局部优化方法^[15]。它使用正定矩阵来近似二阶导数矩阵(Hessian)的逆, 从而简化了运算的复杂度。这种方法只需要使用一个保存后的一阶导数序列就可以完成Hessian矩阵近似, 因此不需要大量的存储。而且此方法推导中使用了秩二校正构造的正定矩阵, 保证了获得的解即使不是最优的下降方向, 也可以保证函数是下降的, 因此对于大规模优化问题, LBFGS是一个较好的选择。

LBFGS算法步骤如下:

(1)给定初始点x₀, 误差值ε > 0, 存储迭代数据(次数m);

(2)迭代次数k=0, 初始海森矩阵H₀=I, 梯度向量r_k=∇f(x₀);

(3)‖ ∇f(x_k₊₁)‖ < ε 成立, 输出最优解x, 否则转入第4步;

(4)计算方向导数P_k=-r_k, 作为迭代方向;

(5)通过公式α _k=argf(x_k+α _kp_k)=argminf(x_k+α p_k)> 0获取步长;

(6)更新权重x, x_k₊₁=x_k+α _kp_k;

(7)如果k> m, 存储近m次向量对, 删除(s_k_-_m, t_k_-_m);

(8)计算并存储s_k=x_k₊₁-x_k, t_k=∇f(x_k₊₁)-∇f(x_k);

(9)* 求取第k步迭代方向的计算量r_k=B_k∇f(x_k);

(10)k=k+1, 转第4步。

* 注意B_k的计算步骤如下[式(10)]

$\begin{array}{l} B_{k} = {v^{T}}_{k - 1} B_{k} V_{k} + ρ_{k - 1} s_{k - 1} s_{k - 1}^{T} = \\ ({v^{T}}_{k - 1} \dots {v^{T}}_{k - m}) B_{i}^{0} ({v^{T}}_{i - m} \dots {v^{T}}_{i - 1}) + \\ ρ_{k - m} ({v^{T}}_{k - 1} \dots {v^{T}}_{k - m + 1}) s_{k - m} {s^{T}}_{i - m} (V_{i - m + 1} \dots V_{i - 1}) + \\ ρ_{k - m + 1} ({v^{T}}_{k - 1} \dots {v^{T}}_{k - m + 2}) s_{k - m + 1} {s^{T}}_{i - m + 1} (V_{i - m + 2} \dots V_{i - 1}) + \\ \dots + ρ_{i - 1} s_{i - 1} {s^{T}}_{i - 1} \end{array}$ (10)

式(10)中, $ρ_{k} = \frac{1}{{t^{T}}_{k} s_{k}}, V_{k} = I - ρ_{k} t_{k} {s^{T}}_{k}$

3 数值实验

目前, 国家相关机构常用的标准光源种类主要有模拟蓝天日光的D65光源, 色温6 500 K; 模拟北方平均太阳光的D75光源, 色温7 500 K; 模拟太阳光的D50光源, 色温5 000 K, 以及模拟各种商业场景的TL84、 U30、 CWF、 U35、 F、 A、 TL83等光源, 还有必要时加入的UV紫外灯光源(365 nm)^{[4, 5]}。生产实践中, 标准光源箱制造商一般以特制荧光灯模拟D65、 D75、 D50等作为标准光源, 因此本工作选用标准A、 D65、 D55、 D50和D75作为目标合成光源。

本节使用Python语言, 以光谱波段315~780 nm, 间隔5 nm(共94个测试点)的标准光谱CIE-A, CIE-D50, CIE-D55, CIE-D65, CIE-D75 为拟合的目标光谱, 编程测试了LLR-LBFGS算法的数值效果。因为带非负约束的LASSO、 RIDGE回归方法是比较有效的确定性回归方法, 所以用来与本算法比较。根据实际工业生产中的式(1)中LED光谱辐射功率峰值P, 峰值波长λ ₀和半宽高Δ λ , 本工作搜集的单色LED光谱共48个, 即 $S (λ_{i}) = [s_{1} (λ_{i}), s_{2} (λ_{i}), \dots, s_{48} (λ_{i})], i = 1, 2, \dots, 94, 即 λ_{1} = 315, λ_{2} = 320, \dots, λ_{94} = 780$ , 因此本次拟合光谱系数矩阵A是94行48列[见式(4)和式(5)]。要求的比例(回归)系数w₁, w₂, …, w₄₈为48个[见式(5)中W]。

表1给出了RMSE和R²数值结果。从表1可以看出, 除去CIE-D75为91.90%外, LLR-LBFGS方法对5个光谱拟合目标的决策系数R²均超过95%。除去CIE-D75的RMSE值超过7外, 其他目标的RMSE评价系数值均小于5。分析发现, 本次收集到的光谱数据波段315~380 nm之间的真实工业数据间隔不均匀, 影响了优化的指标数值。尤其, 在这一波段内遇到有突变点时(见图3中CIE-D65和CIE-D75在380 nm附近的突变点), R²数和RMSE变化更大一些(比如CIE-D75的两个值为0.919 0和7.185 7)。另外, 需要说明的是, 获得上述运算效果的最大运行时间是1.6 s以内。说明本算法运算效果、效率和求解精度较高。

表1 LLR_LBFGS算法拟合光谱曲线效果(48个工业单色LED光谱) Table 1 Fitting results of LLR-LBFGS based on 48 industrial single colour LED spectra

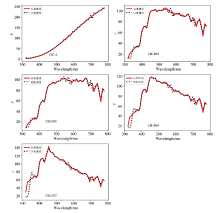	Figure Option View Download New Window
	图3 LLR-LBFGS对5种目标光谱(CIE-A、 CIE-D65、 CIE-D50、 CIE-D55和CIE-D75)拟合效果Fig.3 The fitting results of LLR-LBFGS on CIE-A, CIE-D65, CIE-D50, CIE-D55 and CIE-D75

图3给出了LLR-LBFGS方法对5个光谱拟合目标的拟合效果展示。从标准曲线和拟合曲线拟合度可以看出, 除去对CIE-D65和CIE-D75拟合效果在波长λ < 400 nm效果稍差外, 其他情况下拟合效果较好, 说明LLR-LBFGS算法求取的比例系数精度较高, 与表1数值结果相符。

3.1 LLR-LBFGS与LASSO、 RIDGE方法效果比较

LASSO^{[16, 17]}回归算法与RIDGE回归算法^{[16, 18]}都是在标准线性回归的基础上修改其损失函数 $J = \frac{1}{n} \sum_{i}^{=} (f (x_{i}) - y_{i})^{2} ((x_{i}, y_{i}), i = 1, 2, \dots, n, 为 n$ 对回归数据样本), 即分别加入 L1[式(11)]和L2[式(12)]正则化项的两种经典回归方法, 其损失函数分别为:

LASSO回归损失函数为加入1范数正则项λ ‖ w‖ ₁

$J = \frac{1}{n} \overset{n}{\sum_{i = 1}} (f (x_{i}) - y_{i})^{2} + λ ‖ w ‖_{1}$ (11)

RIDGE回归损失函数为加入2范数正则项λ ‖ w $‖_{2}^{2}$

$J = \frac{1}{n} \overset{n}{\sum_{i = 1}} (f (x_{i}) - y_{i})^{2} + λ ‖ w ‖_{2}^{2}$ (12)

由于正则项的加入使得LASSO回归和RIDGE回归对求取参数的约束比标准回归更灵活^[16], 对数据特征的可解释性可以更符合实际。所以本小节以截距为0, 回归系数要求非负为前提, 通过优选参数对目标光谱拟合问题进行了求解, 并与LLR-LBFGS算法的运行结果进行了对比, 运行时间同样要求限制在1.6 s以内, 运行结果见表2。考虑到本次收集的380 nm以下的目标数据间隔不均匀, 波长小于380 nm的光线为紫外线, 波段380~780 nm的可见光更有实际意义, 因此以下数值实验目标光谱范围均为380~780 nm。

表2 不同算法的结果比较(来自工业单色LED光谱数目: 48, 光谱范围: 380~780 nm) Table 2 Comparison of different methods (48 industrial single colour LED spectra, spectral range: 380~780 nm)

表2给出了LLR-LBFGS算法与LASSO算法、 RIDGE算法的效果对比。从表2可以看到, 对于所有的测试数据, LLR-LBFGS算法性能指标R²和RMSE比LASSO回归算法和RIDGE的对应指标更好。尤其是对于目标光谱CIE-D75, 在近似相同的运行时间内, LLR-LBFGS方法比LASSO和RIDGE方法的R²值分别提了2.45%和4.49%, RMSE值分别降低了17.53%和26.70%。

3.2 LLR-LBFGS和DE、 PSO与GA的效果比较

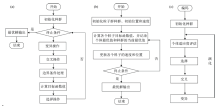
差分进化算法(DE)^[19]、粒子群算法(PSO)^{[14, 20]}和遗传算法(GA)^{[21, 14]}是智能优化算法中比较经典的随机类启发式算法。其中, DE 是一种基于群体的启发式搜索算法, 群中的每个个体对应一个解向量。其进化流程则包括变异、杂交和选择操作, 通过迭代搜索全局最优。详细流程请参考文献[19]。 PSO算法1995年由Eberhart博士和Kennedy博士源于对鸟群捕食行为的研究^[20], 提出的一种进化策略, 其核心是利用群体中的个体对信息的共享, 使整个群体的运动在求解空间中产生从无序到有序的演化过程, 最后获得最优解。 GA 算法^{[14, 21]}是一种基于自然选择和群体遗传机理的搜索算法, 它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象。在利用遗传算法求解时, 每一个可能解都被编码成一个“ 染色体” , 即个体, 若干个个体构成了群体(所有可能解)。三种方法的运行流程见图4(a)、 (b)和(c)。

	Figure Option View Download New Window
	图4 DE (a)、 PSO (b)和GA (c)算法流程图Fig.4 Flow charts of DE (a), PSO (b) and GA (c)

甘汝婷^[7], 郭震宁^[8], 高航^[13]和程真^[5]等分别使用了遗传算法和改进DE算法理论模拟目标光谱的优化问题进行了测试。为了更全面调查LLR-LBFGS的优化性能, 基于实际工业生产数据, 本节对比了其与DE、 PSO和GA的优化效果。需要说明的是, 本节的DE、 PSO和GA算法选择了原文中出现的比较经典的步骤和参数, 设定的运行时间是LLR-LBFGS算法给定时间(1.6 s)的150倍(240 s), 运行结果见表3。这里选择240 s的原因是, 在该时间限制内, DE算法取得了可以接受的运算结果。

表3 LLR-LBFGS 与 GA、 PSO、 DE算法优化效果 Table 3 Comparison of LLR-LBFGS with GA, PSO and DE

从表3可以明显的看出, 与LLR-LBFGS算法相比, DE、 PSO和GA算法运算效果从精确性和精度上相差较多, 说明本算法的有效性。同时也说明基于目标函数分析性质的算法收敛速度要比随机类算法收敛速度快很多。在DE、 PSO和GA三种智能优化算法中, GA算法运行性能最高, 其次是DE算法, PSO算法的运行效果最差。根据实际运行发现, 进一步的设定运行时间, 增加GA种群数量和迭代次数, 还可以进一步提高其运行效果。表3中, PSO运行决策系数中出现了几个负值, 说明这种算法对目标函数的优化准确性较差。

3.3 LLR-LBFGS与LASSO、 RIDGE、 GA、 PSO和DE优化系数比较

为了进一步对比分析LLR-LBFGS与LASSO、 RIDGE、 GA、 PSO和DE对目标光谱的拟合效果。以标准光谱CIE-65为例, 给出了6种方法对于48种单色LED累加拟合目标的权重比例系数(见表4)。从表4可以看到, 由于非负系数的要求, 使得6种算法求取的最优结果不尽相同。其中, 基本PSO算法求取的比例系数多数为0, 再综合表3可以知道, 这种算法对求取变量较多、精度要求较高的问题效果较差。综合累加拟合目标标准光谱CIE-65的几种方法, 可以看出有些单色LED光谱, 比如s₃(λ ), s₆(λ ), s₉(λ ), s₁₁(λ ), s₁₅(λ )等可以省略(其比例系数为0), 而s₂₀(λ ), s₂₁(λ ), s₄₄(λ ), s₄₅(λ )等比较重要(其比例系数比较大), 是组合目标光谱的主要组成部分。实验也发现, 当某些比较重要的基础单色LED光谱缺失时, RMSE误差很难降低, R²也无法更接近1。另外, 确定性方法(LLR-LBFGS与LASSO、 RIDGE)在求取比例系数时, 由于使用了梯度下降方法, 利用了目标函数的分析性质, 有更多的系数被置0处理。而启发式随机算法, 比如GA和DE算法在求取比例系数时, 更多的是通过每个种群个体之间的微调来求取最佳的组合优化解, 所以绝大多数解在[0, 1]之间, 没有0值出现。

表4 LLR-LBFGS与LASSO、 RIDGE、 GA、 PSO和DE对CIE-D65拟合获得的比例系数 Table 4 The coefficients obtained by LLR-LBFGS, LASSO, RIDGE, GA, PSO and DE for CIE-D65

参数	不同算法对目标光谱CIE-65优化比例系数
W_i, i=1, 2, …, 48	LLR-LBFGS	LASSO	RIDGE	GA	PSO	DE
1	0.149 494	0.148 1	0.154 619	0.160 293	0	0.095 988
2	0.066 542	0.068 3	0.060 042	0.046 977	0	0.055 993
3	0	0	0	0.000 004	0	0.040 243
4	0.044 537	0.043 037	0.047 735	0.083 28	0	0.114 629
5	0.190 734	0.191 942	0.189 208	0.131 806	0	0.123 639
6	0	0	0	0.325 05	0	0.116 81
7	0.267 908	0.266 663	0.267 494	0.247 629	0	0.318 617
8	0.509 373	0.509 439	0.499 62	0.470 553	0	0.290 343
9	0	0	0.007 666	0.050 033	0.624 074	0.170 882
10	0.302 364	0.301 824	0.230 43	0.235 041	0	0.044 631
11	0	0	0.053 535	0.012 419	0	0.045 399
12	0.053 434	0.053 082	0.043 578	0.061 457	0	0.094 958
13	0.123 359	0.123 769	0.106 775	0.119 671	0	0.078 764
14	0.108 066	0.119 374	0.129 087	0.058 46	0	0.092 944
15	0	0	0	0.123 661	5	0.127 406
16	0.174 739	0.172 544	0.197 899	0.169 601	0	0.026 713
17	0.716 934	0.709 881	0.565 475	0.472 622	0	0.865 529
18	0.557 555	0.564 455	0.853 983	0.932 778	5	0.205 006
19	0.147 404	0.147 26	0.027 687	0.007 972	0	0.280 016
20	2.771 394	2.747 446	2.676 498	2.668 158	5	2.667 397
21	1.926 989	1.915 592	1.971 877	1.924 727	0.357 824	1.944 6
22	0.203 549	0.181 776	0.117 972	0.216 37	0.496 222	0.161 468
23	0.106 964	0.136 122	0.198 307	0.103 501	0	0.173 212
24	0.306 556	0.265 779	0.258 822	0.256 022	0	0.194 931
25	0.139 58	0.159 441	0.105 754	0.161 24	0	0.089 468
26	0.000 078	0	0.069 774	0.054 117	0.584 067	0.162 082
27	0.328 888	0.315 184	0.265 822	0.228 472	0	0.165 598
28	0.019 304	0.023 951	0.059 304	0.073 506	0	0.095 22
29	0.186 185	0.185 323	0.152 15	0.153 161	0	0.112 312
30	0.026 961	0.025 079	0.073 163	0.048 158	0	0.118 25
31	0.111 517	0.113 431	0.075 435	0.102 051	0	0.071 945
32	0	0	0.023 861	0.010 644	0	0.008 247
33	0.022 539	0.019 39	0.034 412	0.026 618	0	0.043 497
34	0.059 697	0.066 565	0.085 738	0.097 681	0	0.093 353
35	0	0	0.087 68	0.068 444	0	0.059 199
36	0.316 712	0.375 167	0.109 963	0.106 117	0	0.061 207
37	0.004 324	0.055 804	0.103 388	0.109 253	0	0.099 829
38	0.399 257	0	0.079 822	0.071 17	1.076 024	0.204 278
39	0.014 184	0.095 254	0.106 43	0.110 812	0	0.061 245
40	0.024 964	0.044 024	0.041 311	0.044 231	0	0.002 156
41	0	0	0.092 052	0.048 795	0	0.467 516
42	0.052 302	0.057 388	0.051 265	0.053 397	0	0.015 714
43	0.043 593	0.038 229	0.020 343	0.039 09	0.107 116	0.151 685
44	1.323 731	1.338 566	1.336 775	1.339 181	1.429 283	1.167 068
45	5	0	0.070 731	4.999 391	0	4.342 073
46	0.236 978	0	0.003 301	4.980 391	5	2.732 816
47	0.537 819	0.490 083	0.442 01	0.567 699	0	0.533 419
48	0.584 4	0.600 378	0.639 967	0.534 321	0	0.552 944

表4 LLR-LBFGS与LASSO、 RIDGE、 GA、 PSO和DE对CIE-D65拟合获得的比例系数 Table 4 The coefficients obtained by LLR-LBFGS, LASSO, RIDGE, GA, PSO and DE for CIE-D65

4 结论

提出了一种利用目标函数数学解析性质的两阶段全局优化算法LLR-LBFGS, 该方法在初始点的产生与加快局部最优解的收敛速度和求解精度上, 利用了不同算法的优势。较大地改进了目标函数全局最优解的质量。针对工业界存在的目标光源光谱拟合问题, 在求解目标光谱的非负比例系数问题时, 与LASSO和RIDGE两种经典的线性回归算法相比, LLR-LBFGS全局解的精度更高。与三种随机类算法(PSO、 DE和GA)对比表明, LLR-LBFGS算法求解速度更快。本方法不但对解决目标光谱问题有普适性。同时, 研究表明充分利用目标函数的数学解析性质, 把成熟的理论融合到新设计的方法中, 能较大改善传统算法的性能。当然, 在允许的条件下, 以算法获得的全局解的精度、收敛速度和决策系数为衡量指标, 依据本算法设计思路, 可以重新构建LLR-LBFGS第一阶段或第二阶段的实现方法, 从而组合出不同的全局优化策略。

参考文献

文献列表

[1]	SONG Peng-cheng, WEN Shang-sheng, CHEN Ying-cong(宋鹏程, 文尚胜, 陈颖聪). Acta Optica Sinica(光学学报), 2015, 5(9): 305. [本文引用:1]
[2]	CHI Nan, LU Xing-yu, WANG Cai, et al(迟楠, 卢星宇, 王灿, 等). Chinese Journal of Laser(中国激光), 2017, 44(3): 7. [本文引用:2]
[3]	SU Shi, ZHANG Guo-yu, WANG Ling-yun, et al(苏拾, 张国玉, 王凌云, 等). Laser & Optoelectronics Progress(激光与光电子学进展), 2018, 55(7): 40. [本文引用:1]
[4]	International Commission on Illumination. CIE 015, Colorimetry, 4th ed. Commission Internationale de L'Eclairage. 2018. [本文引用:2]
[5]	CHENG Zhen, SI Gan-shang, LI Zhen-gang, et al(程真, 司赶上, 李振钢, 等). Acta Optica Sinica(光学学报), 2022, 42(9): 1. [本文引用:7]
[6]	SHEN Hai-ping, FENG Hua-jun, PAN Jian-gen, et al(沈海平, 冯华君, 潘建根, 等). Proceedings of Approaching CIE 26th——Academic Annual Conference of China Lighting Society (2005)[走近CIE 26th中国照明学会(2005)学术年会论文集], 2005, 83. [本文引用:2]
[7]	GAN Ru-ting, GUO Zhen-ning, LIN Jie-ben, et al(甘汝婷, 郭震宁, 林介本, 等). Acta Photonica Sinica(光子学报), 2014, 47(7): 6. (doi: DOI:10.3788/gzxb20144307.0730003). [本文引用:3]
[8]	GUO Zhen-ning, LIAO Xuan, GAN Ru-ting, et al(郭震宁, 廖炫, 甘汝婷, 等)Journal of Huaqiao University(Natural Science) [华侨大学学报(自然科学版)], 2016, 37(6): 731. [本文引用:3]
[9]	ZHANG Yi-wen, XU Lin, WAN Song(张译文, 徐林, 万松). Acta Photonica Sinica(光子学报), 2013, 42(5): 596. [本文引用:2]
[10]	TANG Lu-yao, SU Cheng-yue, CHEN Shao-fan, et al(汤露瑶, 苏成悦, 陈少藩, 等). China Illuminating Engineering Journal(照明工程学报), 2017, 28(5): 4. [本文引用:2]
[11]	GAO Yuan, DONG Jian-fei, WU Hai-ning, et al(高源, 董建飞, 吴海宁, 等). China Light & Lighting(中国照明电器), 2015, (11): 15. [本文引用:2]
[12]	NI Jun-xiong, BAI Ting-zhu, XU Ying-ying(倪俊雄, 白廷柱, 徐英莹). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2012, 32(6): 1606. [本文引用:2]
[13]	GAO Hang, XUE Ling-yun(高航, 薛凌云). Laser & Optoelectronics Progress(激光与光电子学进展), 2017, 54(7): 294. [本文引用:2]
[14]	Li W, Wang G G, Gand omi A H. Archives of Computational Methods in Engineering, 2021, 28: 3781. [本文引用:4]
[15]	Byrd R H, Lu P, Nocedal J, et al. SIAM Journal on Scientific Computing. 1995, 16(5): 1190. [本文引用:3]
[16]	Psaros A F, Meng X, Zou Z, et al. Journal of Computational Physics, 2023, 477: 111902. [本文引用:3]
[17]	Tibshirani R. Journal of the Royal Statistical Society, Series B: Statistical Methodology, 1996, 58(1): 267. [本文引用:1]
[18]	Hoerl A E, Kennard R W. Technometrics, 1970, 12: 55. [本文引用:1]
[19]	Storn R, Price K. Journal of Global Optimization, 1997, 11(4): 341. [本文引用:2]
[20]	Kennedy J, Eberhart R. Proceedings of ICNN'95—International Conference on Neural Networks, 1995, 4: 1942. [本文引用:2]

2015

0.0

... 通过使用LED作为光源配比生成的不同标准光源, 已经广泛地应用于纺织印染、印刷、油漆、造纸、食品、植物保护和设施农业等行业^[1,2,3] ...

2017

0.0

... 通过使用LED作为光源配比生成的不同标准光源, 已经广泛地应用于纺织印染、印刷、油漆、造纸、食品、植物保护和设施农业等行业^[1,2,3] ...

... 随着半导体技术的发展, 作为第四代照明光源的LED有发光效率高、使用寿命长、性能稳定、波长种类丰富、单色性好、半峰全宽(FWHM)窄的优点和发光光谱等特性能较好地控制^[2], 且这些特性可以组合不同波段LED模拟产生连续分布的目标光谱^[5] ...

2018

0.0

... 通过使用LED作为光源配比生成的不同标准光源, 已经广泛地应用于纺织印染、印刷、油漆、造纸、食品、植物保护和设施农业等行业^[1,2,3] ...

2018

0.0

... 国际照明委员会CIE规定了一些标准照明体的相对光谱功率分布^[4] ...

... 模拟太阳光的D50光源, 色温5 000 K, 以及模拟各种商业场景的TL84、 U30、 CWF、 U35、 F、 A、 TL83等光源, 还有必要时加入的UV紫外灯光源(365 nm)^[4,5] ...

2022

0.0

... 程真设计了改进的差分进化算法(DE)解决实验室目标光谱数据的匹配优化问题, 取得了较好的效果^[5] ...

... 因此, 目标光谱匹配就是给定需要拟合的某种标准(样本)光谱, 选择比例系数不同的LED单色光谱, 使得线性累加后的混合光谱尽量与标准光谱一致^{[5, 7,8,9,10,11,12]} ...

... 3 评价指标根据线性回归或线性拟合中, 衡量拟合效果的均方根误差大小的直接指标为式(8)^[5] ...

... 通过衡量拟合曲线与标准数据的相似程度的评价光谱匹配度指标见式(9)^[5] ...

... 模拟太阳光的D50光源, 色温5 000 K, 以及模拟各种商业场景的TL84、 U30、 CWF、 U35、 F、 A、 TL83等光源, 还有必要时加入的UV紫外灯光源(365 nm)^[4,5] ...

... 甘汝婷^[7], 郭震宁^[8], 高航^[13]和程真^[5]等分别使用了遗传算法和改进DE算法理论模拟目标光谱的优化问题进行了测试 ...

2005

0.0

... 沈海平等开展了LED光谱数学模型创建研究为光谱合成和理论研究奠定了基础^[6] ...

... 1 单色LED光谱曲线基于高斯分布函数的单色LED光谱曲线模型见式(1)^[6], 单个LED在光轴方向上的辐射强度为 ...

2014

0.0

... 5标准太阳光的匹配时, 提出了简单遗传算法作为光谱匹配方法, 通过求解超定方程组的非负最小二乘解, 优化不同峰值波长、峰值波长间隔、半高宽的单色LED匹配光源组合, 达到光源光谱匹配的目的^[7] ...

... 甘汝婷^[7], 郭震宁^[8], 高航^[13]和程真^[5]等分别使用了遗传算法和改进DE算法理论模拟目标光谱的优化问题进行了测试 ...

2016

0.0

... 郭震宁等优化了单色发光二极管(LED)匹配光源组合, 实现用白光LED取代部分单色LED模拟太阳光谱^[8] ...

... 甘汝婷^[7], 郭震宁^[8], 高航^[13]和程真^[5]等分别使用了遗传算法和改进DE算法理论模拟目标光谱的优化问题进行了测试 ...

2013

0.0

... 张译文等以最小二乘法和高斯分布数学模型为基础, 理论上实现了非均匀间隔峰值波长的光谱拟合, 从而指导LED的种类选择及其所需的驱动电流值, 并通过实验论证了其可行性^[9] ...

2017

0.0

... 汤露瑶等选用了三种不同色温下的太阳光谱作为目标拟合光谱, 借助Matlab优化工具箱中的fmincon 函数求解了不同目标光谱下各组LED的功率组合系数^[10] ...

2015

0.0

... 高源等运用线性规划方法对各通道LED配比进行优化, 实现了LED混光光源的目标光谱^[11] ...

2012

0.0

... 倪俊雄等采用最小二乘法成功拟合出几种特征明显的常见标准光源光谱^[12] ...

2017

0.0

... 高航采用改进的遗传算法与神经网络结合设计了求取光谱配比系数方法, 取得了一定的效果^[13] ...

... 甘汝婷^[7], 郭震宁^[8], 高航^[13]和程真^[5]等分别使用了遗传算法和改进DE算法理论模拟目标光谱的优化问题进行了测试 ...

2021

0.0

... 随机类启发式方法^[14](比如遗传算法、粒子群方法、差分算法和模拟退火算法等)求解这类问题速度慢, 精度低 ...

... 2 LLR-LBFGS和DE、 PSO与GA的效果比较差分进化算法(DE)^[19]、粒子群算法(PSO)^{[14, 20]}和遗传算法(GA)^{[21, 14]}是智能优化算法中比较经典的随机类启发式算法 ...

... GA 算法^{[14, 21]}是一种基于自然选择和群体遗传机理的搜索算法, 它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象 ...

1995

0.0

... 该方法借助于最小二乘通用理论解作为解决问题的初始点(由于非负解的要求, 该理论解不一定符合实际要求), 然后利用梯度优化方法LBFGS^[15]求取局部最优解的精度高和收敛速度快的优势获得最佳配比比例 ...

... 利用目标函数的分析性质, 首先求得式(6)的最小二乘意义下最优解[式(7)], 以式(7)的解为初始点, 设计带约束的拟牛顿法BFGS优化算法^[15]求解问题非负解 ...

... 其中, LBFGS算法是由Broyden、 Fletcher、 Goldfarb和Shanno四人提出的拟牛顿局部优化方法^[15] ...

2023

0.0

... 1 LLR-LBFGS与LASSO、 RIDGE方法效果比较LASSO^[16,17]回归算法与RIDGE回归算法^{[16, 18]}都是在标准线性回归的基础上修改其损失函数 J=1n∑i=1n(f(xi)-yi)2((xi,yi),i=1,2,…,n,为n对回归数据样本), 即分别加入 L1[式(11)]和L2[式(12)]正则化项的两种经典回归方法, 其损失函数分别为: ...

... 由于正则项的加入使得LASSO回归和RIDGE回归对求取参数的约束比标准回归更灵活^[16], 对数据特征的可解释性可以更符合实际 ...

1996

0.0

1970

0.0

1997

0.0

... 详细流程请参考文献[19] ...

1995

0.0

... PSO算法1995年由Eberhart博士和Kennedy博士源于对鸟群捕食行为的研究^[20], 提出的一种进化策略, 其核心是利用群体中的个体对信息的共享, 使整个群体的运动在求解空间中产生从无序到有序的演化过程, 最后获得最优解 ...