引用本文
王洋, 林振衡, 郑志杰, 谢海鹤, 聂泳忠. 基于THz-TDS的氟橡胶材料寿命预测方法[J]. 光谱学与光谱分析, 2024,44(6): 1578-1583.
WANG Yang, LIN Zhen-heng, ZHENG Zhi-jie, XIE Hai-he, NIE Yong-zhong. Lifetime Prediction Method for Fluororubber Based on Terahertz Time Domain Spectrum Technology[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1578-1583.
Doi:10.3964/j.issn.1000-0593(2024)06-1578-06  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于THz-TDS的氟橡胶材料寿命预测方法
王洋1, 林振衡2,1,*, 郑志杰1, 谢海鹤2, 聂泳忠3
1. 福州大学机械工程及自动化学院, 福建 福州 350108
2. 莆田学院新工科产业学院, 福建 莆田 351100
3. 西人马联合测控(泉州)科技有限公司, 福建 泉州 362011
*通讯作者 e-mail: 147121176@qq.com

作者简介: 王 洋, 1995年生, 福州大学机械工程及自动化学院硕士研究生 e-mail: 1643907452@qq.com

收稿日期: 2022-10-06 修回日期: 2024-01-31
基金: 国家自然科学基金项目(62103209), 福建省科技厅高校产学合作项目(2021H6038)资助
摘要

氟橡胶(FKM)材料具有优异的耐热性、 耐腐蚀性、 耐油性, 已成为航空、 航天、 石油、 机械等领域的热门材料。 但由于传统的FKM材料寿命检测方法存在离线检测、 会损伤待测材料、 检测步骤繁琐、 检测效率低等缺点, 目前在FKM材料实际应用中往往采用定期更换的办法, 易造成材料浪费与经济损失。 提出了一种基于太赫兹时域光谱检测技术(THz-TDS)的FKM材料使用寿命预测新方法。 首先, 通过对在热空气老化箱中经不同温度、 不同时长热氧老化处理的FKM材料进行THz-TDS透射检测, 获得其对应的时域光谱图, 提取相应的电流峰峰值, 即在一个透射采样周期中最大的探测电流值与最小的探测电流值之间的差值; 再将不同老化温度的FKM材料的THz时域波形的峰峰值与老化时间进行拟合, 发现FKM样品时域光谱的峰峰值随着老化时间的延长呈下降趋势, 且老化温度越高该下降趋势越明显。 在200、 300和360 ℃这三个老化温度下的拟合直线的相关系数分别高达0.973 4、 0.982 1和0.993 5。 其次, 根据阿伦尼乌斯公式的基本思想, 建立起以时域光谱峰峰值为参考标准的FKM材料寿命预测数学模型。 利用时域光谱峰峰值的FKM材料使用寿命预估办法获得的老化反应速率常数的对数与老化温度倒数关系拟合直线的相关系数达0.996 9。 最后, 采用力学拉伸测量FKM材料断裂伸长率的办法, 对其基于THz-TDS的使用寿命预估数学模型中的THz-TDS峰峰值失效临界值进行验证, 可得构建的基于THz-TDS的FKM材料使用寿命预估模型成立且正确。 研究结果表明: 将THz-TDS检测方法应用到FKM材料寿命检测具有较高的准确性, 且该方法具有无损、 高效、 操作简便、 适用性广等优点, 为FKM材料制品在线检测和寿命预测提供可能性, 也为其他非极性材料和电介质材料的寿命预测方法研究提供参考。

关键词: 太赫兹时域光谱; 氟橡胶; 寿命预测; 峰峰值
中图分类号:O433.4 文献标志码:A
Lifetime Prediction Method for Fluororubber Based on Terahertz Time Domain Spectrum Technology
WANG Yang1, LIN Zhen-heng2,1,*, ZHENG Zhi-jie1, XIE Hai-he2, NIE Yong-zhong3
1. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108, China
2. New Engineering Industry College, Putian University, Putian 351100, China
3. Xirenma United Measurement and Control (Quanzhou) Technology Co., Ltd., Quanzhou 362011, China
*Corresponding author
Abstract

Fluorine rubber (FKM) material has excellent heat resistance, corrosion resistance, oil resistance and more, making it a popular material in aviation, aerospace, petroleum, machinery and other industries. However, the traditional service life testing method for FKM materials has disadvantages, such as damage to the material to be tested, complicated operation steps, and low testing efficiency. Therefore, in practical applications, FKM is often replaced directly and regularly, but it has a higher possibility of harming the environment by pollution. A new method for predicting the service life of FKM materials using terahertz time-domain spectroscopy (THz-TDS) was proposed. At firstly, Perform THz-TDS detection on the FKM material that has been subjected to different temperatures and different periods in a hot air aging box, obtain its corresponding time-domain spectrum, and extract the corresponding peak-to-peak value, that is, the difference between the maximum detection current value and the minor detection current value in a transmission sampling cycle. Fitting the peak-to-peak value of the THz time-domain waveform of the FKM material with different aging temperatures and the aging time, it could be seen that the peak-to-peak value of the time-domain spectrum of the FKM sample decreases with the aging time, and the higher the aging temperature, the downward trend was more prominent. The correlation coefficients of the fitted straight lines at the three aging temperatures of 200, 300 and 360 ℃ were as high as 0.973 4, 0.982 1 and 0.993 5, respectively. Secondly, according to the basic idea of the Arrhenius formula, a mathematical model of FKM material life prediction was established with the peak-to-peak value of the time domain spectrum as the reference standard. The correlation coefficient of the fitted straight line of the relationship between the logarithm of the aging reaction rate constant and the reciprocal of the aging temperature obtained using the time-domain spectral peak-to-peak service life estimation method was 0.996 9. Finally, the critical value of the THz-TDS peak-to-peak failure in the THz-TDS-based service life prediction mathematical model was verified by measuring the elongation at the break of the FKM material by mechanical stretching. The FKM based on -the constructed THz-TDS could be obtained, and the material life estimation model was established with higher correct efficiency. The research results show that applying the THz-TDS detection method to FKM material life detection has high accuracy. In addition, THz-TDS detection has the advantages of non-destructiveness, high efficiency, simple operation-wide applicability, etc., which can provide online detection and life prediction for FKM material products. It also references studying life prediction methods for other non-polar and dielectric materials.

Keyword: Terahertz time domain spectroscopy; Fluororubber; Lifetime prediction; Peak to peak value
引言

氟橡胶(FKM)材料是国防尖端工业中不可或缺的关键材料。 它具有优异的耐热性、 耐腐蚀性、 抗氧化性能、 耐油性[1, 2, 3], 被广泛应用于航空、 航天、 汽车、 石油等领域的胶管、 垫圈、 密封圈等构件的制造。 例如, 可用作航空发动机燃料的密封和减震材料[4, 5, 6]。 尽管FKM性能相对稳定, 但在使用过程中也会发生老化失效, 存在安全隐患。 因此, 对FKM进行老化寿命预测十分重要。

加速老化实验是寿命预测的重要工程手段, 可以在较短时间内准确预估器件、 部件或产品的寿命[7, 8]。 目前橡胶材料老化寿命预测方法主要是通过热氧高温加速老化试验与力学性能检测相结合来进行[9, 10, 11, 12, 13, 14], 不仅操作繁琐、 检测周期长、 准确度低, 且会对被测的橡胶样品造成损伤, 无法实现在线无损检测。

太赫兹(THz)波是一种频率介于0.1~10 THz的电磁波, 具有毫米波和红外光波的特征。 由于THz光谱的幅度、 相位和时间等参数包含着被测物体丰富的物理、 化学和结构信息, 因此THz光谱可用于检测相关材料的属性。 太赫兹时域光谱检测技术(THz-TDS)是一种基于相干探测原理的光谱技术, 具有无损、 操作简便、 适用性广等优点[15, 16, 17]。

太赫兹时域光谱峰峰值是指在一个样品的光谱采样周期内最大的探测电流值与最小的探测电流值之间的差值。 而阿伦尼乌斯公式是瑞典物理化学家阿伦尼乌斯提出的化学反应速率常数随温度变化关系的经验公式。 研究证明: 阿伦尼乌斯公式适用范围广, 不仅适用于气相反应, 而且适用于液相反应和大部分复项催化反应, 大部分橡胶材料老化速率随温度的变化规律可以用阿伦尼乌斯公式进行描述。 本工作通过透射式THz-TDS系统采集经过热氧老化处理的FKM材料的THz时域光谱, 研究其光谱峰峰值与老化程度之间的规律性, 建立氟橡胶寿命预测阿伦尼乌斯数学模型, 从而获得一种更加简便、 准确、 高效、 无损的FKM材料寿命预测方法。

1 实验部分
1.1 原理

THz波对许多非极性材料和电介质材料具有很强的穿透性, 且在时间和空间上存在较强相干性, 通过测量材料THz时域波形便可以获得振幅及相位信息。 橡胶材料的热氧老化在本质上是橡胶结构中的不饱和分子结构受到破坏或氧原子的入侵, 热氧作用导致橡胶分子链结构发生断裂或交联, 产生离子形式的自由基[18, 19, 20]。 这种变化会导致橡胶材料在THz场中的分子振动模式和极化模式发生改变, 并且这些改变会反映在测得的各项参数上。 因此, THz-TDS技术可以用于对FKM材料进行检测。

1.2 样品制备

将FKM材料按照GB/T 528— 1992的要求进行切割, 以便于后续使用机械力学检测方式对预测结果进行对比验证, 裁刀符合GB 9865的要求。 为了确保实验数据的准确性和实验的可重复性, 对应相同老化温度和时间条件各制作5个样品。

按照GB/T 3512— 2014《硫化橡胶或热塑性橡胶热空气加速老化和耐热实验》的标准, 将裁切好的哑铃状的FKM材料样品依次等距放入电热鼓风箱进行热空气加速老化实验。 将老化箱温度分别调定为200、 300和360 ℃, 通过鼓风装置来控制并保持老化箱内部的空气流通和含氧量, 每隔一定时间取出5个样品进行THz-TDS光谱检测, 详见表1。

表1 不同热氧老化温度下的取样时间 Table 1 Sampling time at different thermal oxidative aging temperatures
1.3 样品测试

采用THz-TDS透射检测方式对加速老化的FKM样品进行时域光谱检测。 在室温条件(约25 ℃)下, 整个实验光路处于密封实验箱中, 箱内充满高纯氮气, 湿度控制在≤ 10%。 将待测样品夹持在置物台上, 保持样品处在THz波的焦点上, 开启THz-TDS检测系统, 获得样品的THz时域光谱。

1.4 模型构建

1.4.1 数据预处理

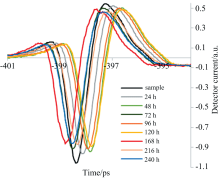
以上图1、 图2和图3分别为FKM在不同老化温度条件下, 间隔一定时间取出后测得的THz-TDS时域光谱图。 其中, sample为未经加速老化的FKM材料样品的时域光谱曲线。 每条曲线均为5个同等实验条件下的样品测得的光谱数据取平均值后得到的拟合曲线。 观察曲线, 可见受到相同老化温度不同老化时间的样品在波形上存在规律: 相同老化温度的FKM样品的时域光谱的最大值和峰峰值随着老化时间的增长均呈现逐渐降低的趋势。

图1 老化温度为200 ℃样品的时域光谱(局部)Fig.1 Time-domain spectra (part) of samples aged at 200 ℃

图2 老化温度为300 ℃样品的时域光谱(局部)Fig.2 Time-domain spectra (part) of samples aged at 300 ℃

图3 老化温度为360 ℃样品的时域光谱(局部)Fig.3 Time-domain spectra (part) of samples aged at 360 ℃

将各组样品光谱信号的峰峰值分别列于表2。

表2 不同老化程度FKM的时域光谱的峰峰值(单位: arb.units) Table 2 Peak-to-peak value of time-domain spectrum of FKM with different aging degrees (unit: arb.units)

为了更明显地观察到样品波形与老化温度和老化时间之间的内在关联性, 现将不同老化温度的FKM材料的THz时域波形的峰峰值与老化时间进行拟合, 得到图4。

图4 热氧老化对FKM材料时域光谱峰峰值的影响
由图4可见: 对应这三个热氧老化温度, FKM样品时域光谱的峰峰值随着老化时间的延长均呈下降趋势, 且老化温度越高下降趋势越明显; 相同老化时间的FKM样品的时域光谱的峰峰值随着老化温度的升高呈现逐渐降低的趋势。 究其原因, 应是 FKM 材料样品在经历高温老化时, 分子结构会进一步发生二次硫化、 物理缠点解缠和降解作用, 使得材料呈现疏松状态甚至出现孔洞, 从而导致 THz 波在材料中进行了多次复杂的反射, 增大了吸收可能, 导致峰峰值随着加热温度增大、 加热时间增长而下降。Fig.4 Effect of thermal oxidative aging on peak-to-peak value of time-domain spectrum of FKM material

1.4.2 寿命预测数学模型

由图4可知, FKM材料在老化过程中的一个表现就是其THz-TDS的峰峰值下降。 因此, 利用FKM材料的时域光谱峰峰值变化情况可预估其使用寿命, 一般经验表达式为

f(P)=Bexp(-Ktα)(1)

式(1)中: P为FKM材料经过t时间热氧老化之后的老化特性指标; B为试验常数; K为老化反应速率常数; t为老化时间, 单位为h; α 为老化常数, 可以按照逼近法进行估算。

对时域光谱峰峰值来说, f(P)=P/P0, P为某时刻FKM的时域光谱峰峰值, P0为FKM样品初始的时域光谱峰峰值。

式(1)中的老化反应速率常数K与老化热力学温度T之间的关系符合阿伦尼乌斯公式[21, 22]

K=Aexp(-E/RT)(2)

式(2)中: A为频率因子, 单位为h-1; E为表观活化能, 单位为J· mol-1; R为气体常数, 8.314 J· mol-1; T为老化温度, 单位为K。

对式(1)两边取对数后便可得到式(3)

lnf(P)=lnB-Ktα(3)

令y=lnf(P), a=lnB, b=-K, x=tα , 则式(3)可转化为式(4)。

y=a+bx(4)

对式(2)两边取对数, 变换后可得式(5)

lnK=lnA-ERT(5)

令y=lnK, c=lnA, d=- ER, x=T-1, 则可以得式(6)

y=c+dx(6)

以lnK对T-1绘制曲线, 经直线拟合便可以得到c和d的值, 从而计算得到A和E的值, 分别代入式(2)中可以得到不同老化温度下的老化速率常数K, 最后利用式(1), 便可以得到不同老化温度下的使用寿命。

计算α 应当采用逐次逼近法, 从取值α 为0.5及0.51开始计算尝试, 再进行直线二乘法拟合, I可以按照式(7)进行计算

I=∑i=1m∑j=1n(Pij-P̅ij)2(7)

式(7)中: Pij为测得蹬老化温度为i、 老化时间为j的样品的THz时域光谱的峰峰值; P̅ij为预测相关系数为α 时直线计算得到的THz时域光谱的峰峰值。 I值越接近于0时说明线性拟合效果越好, 选择此时的α 值为后期计算时的数值。

将三个老化温度下的时域光谱峰峰值与老化时间进行直线拟合后得到图5, 图中的三条直线对应的数据如表3所示。

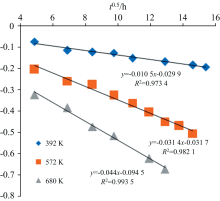图5 FKM材料时域光谱峰峰值与老化时间的关系Fig.5 The relationship between the peak-to-peak value of the time-domain spectrum and the aging time of FKM material

表3 FKM老化后时域光谱峰峰值与时间拟合后直线的数据 Table 3 The linear data of the time-domain spectrum peak-to-peak value and time fitting after FKM aging

通过图5可以看出: 三个老化温度下的拟合直线的相关系数分别高达0.973 4、 0.982 1和0.993 5。 因此, 这三条拟合直线均具有显著相关性。 通过计算可得到FKM样品的使用寿命公式中的B, 为了更具普遍性, B值取三个老化温度下的平均值, 得到B=0.949 7。

利用表5得到的数据绘制曲线如图6所示。

图6 反应速率常数对数与温度倒数的关系
阿伦尼乌斯经验公式的前提假设认为活化能E被视为与温度无关的常数, 在一定温度范围内与实验结果符合, lnk与1/T就是一条很好的直线。 由图6可知, 利用时域光谱的峰峰值的使用寿命预估手段获得的老化反应速率常数的对数与老化温度的倒数的关系如式(8)所示Fig.6 The relationship between the logarithm of reaction rate constant and the reciprocal of temperature
y=-1276.5x-1.2458(8)

该拟合直线的相关系数R2=0.996 9。 因此, 该拟合线具有显著相关性。

由此也可以计算出以时域光谱峰峰值为评价标准的FKM材料寿命预测中的频率因子A和表观活化能E分别是: A=0.287 7 h-1, E=10.6 kJ· mol-1。

2 结果与讨论

由于材料的断裂伸长率能够比较直观地反映其拉伸变形能力, 与有效使用寿命密切相关。 因此, 通过力学拉伸测量FKM材料断裂伸长率的办法对其基于THz-TDS的使用寿命预估数学模型中的THz-TDS峰峰值失效临界值进行验证。

研究表明, 当断裂伸长率降至原来的50%时可看成是该橡胶材料构件性能失效的临界, 按照常规寿命预测方法, 此时的f(p)=0.5。 本研究选用的FKM材料原始断裂伸长率为286%, 因此, 当断裂伸长率低于143%时, 即可认为该FKM材料样本已失效。

老化实验所用的FKM材料已裁切成标准拉伸实验所需的哑铃状, 使用台湾东日检测设备有限公司生产的DR-509型拉力试验机对样品进行拉力试验, 拉伸速率设定为500 mm· min-1, 测定的拉断伸长率记录如表4所示。 可以看出, 样品的断裂伸长率会随着老化温度的升高和老化时间的延长而逐渐降低, 直至低于性能失效的临界。 因而可以判定不同程度热氧老化的FKM材料在断裂伸长率和THz-TDS峰峰值上都有着相应的体现, 且两者存在良好的对应关系。

表4 热氧老化温度、 时间对FKM材料断裂伸长率的影响 Table 4 Effect of thermal oxidative aging temperature and time on elongation at break of FKM materials

如表4所示, 当断裂伸长率为143%时, 所对应材料的THz-TDS峰峰值大约为1 arb.units, 此时的f(p)=0.626, 即老化后的THz-TDS峰峰值降低为初始峰峰值的62.6%。

由此可计算出, 当老化温度为300 ℃时, 经计算可得老化反应速率常数K=0.030 97, 则该FKM材料样品的THz-TDS峰峰值下降到初始的62.6%所需时间大约为181 h, 也即热氧老化温度为300 ℃时, FKM材料的使用寿命大约为181 h。 对照上表4可知, 当老化温度为300 ℃时, 大约在第168 h到第192 h之间的某一时刻材料的断裂伸长率下降到初始的143%。 因此两种测量方式得出的结论相符合。

进一步以上述寿命预测方法做验证性实验, 若热氧老化温度为450 ℃时, 经计算可得老化反应速率常数K=0.063 29, 代入式(3)可计算得到该FKM样品THz-TDS峰峰值下降到初始的62.6%所需时间大约为43 h。 在验证实验中, 将按标准裁切的FKM材料样品进行450 ℃的热氧老化43 h后取出, 静置至样品温度降为室温后对其进行拉断伸长率检测, 测得该样品的拉断伸长率为142%, 该数值与预测结果接近, 因此可以认定本工作构建的基于THz-TDS的FKM材料使用寿命预估模型成立且正确。

3 结论

通过实验发现FKM材料的热氧老化程度与其THz时域光谱的最大值、 峰峰值等光学参数之间存在特定的关联性, 也即: 相同老化时间的FKM样品的时域光谱的最大值和峰峰值随着老化温度的升高均呈现逐渐降低的趋势; 相同老化温度的FKM样品的时域光谱的最大值和峰峰值随着老化时间的增长均呈现逐渐降低的趋势。 据此, 按照阿伦尼乌斯公式的基本路径提出并构建了基于THz-TDS的FKM材料热氧老化寿命预估数学模型。 通过对不同老化程度的FKM材料的拉断伸长率的测量进行验证, 测得的样品的拉断伸长率与根据得到的数学模型预测结果接近。 实验表明: 相较于传统的橡胶材料寿命预测方法, 本文提出的FKM材料寿命预测方法不仅预测精度高, 并且具有无损、 操作简便、 高效等优点, 为氟橡胶材料制品在线检测和寿命预测提供了新的方法。

参考文献
[1] ZHANG Jia-qi, JIA Xian-zhao, GUAN Yan-hui, et al(张嘉琦, 贾现召, 关颜慧, 等). Lubrication Engineering(润滑与密封), 2022, 47(6): 108. [本文引用:1]
[2] REN Hui-fang, JIANG Jie-feng, CHEN Wei-feng(任慧芳, 蒋杰峰, 陈伟峰). Organo-Fluorine Industry(有机氟工业), 2017, (4): 36. [本文引用:1]
[3] XING Hua-yan, ZHANG Jian-xin, CAI Chun-yang(邢华艳, 张建新, 蔡醇洋). Organo-Fluorine Industry(有机氟工业), 2015, (3): 61. [本文引用:1]
[4] YANG Fan, CHEN Feng-bo, WANG Teng, et al(杨璠, 陈风波, 王腾, 等). Chemistry and Adhesion(化学与黏合), 2019, 41(1): 62. [本文引用:1]
[5] WANG Jing, HAN Xiu-feng, LIAN Yi-long, et al(王婧, 韩秀峰, 廉一龙, 等). China Synthetic Rubber Industry(合成橡胶工业), 2021, 44(2): 150. [本文引用:1]
[6] REN Ling-shan, WANG Wen-dong(任凌山, 王文东). Organo-Fluorine Industry(有机氟工业), 2021, (4): 43. [本文引用:1]
[7] HAN Jian-li, CHEN Hong-guang, LI Jian-hua(韩建立, 陈洪光, 李建华). Journal of Naval Aeronautical and Astronautical University(海军航空工程学院学报), 2013, 28(2): 172. [本文引用:1]
[8] GAO Xiao-min, ZHANG Xiao-hua(高晓敏, 张晓华). Chinese Polymer Bulletin(高分子通报), 2010, (2): 80. [本文引用:1]
[9] LIU Xiao-dan, XIE Jun-jie, FENG Zhi-xin, et al(刘晓丹, 谢俊杰, 冯志新, 等). Synthetic Materials Aging and Application(合成材料老化与应用), 2014, 43(1): 69. [本文引用:1]
[10] Lee S Y, Eom S B, Won J S, et al. Fibers and Polymers, 2021, 22(3): 639. [本文引用:1]
[11] MA Yan, FENG De-he, WANG Feng, et al(马妍, 冯德和, 王峰, 等). Special Purpose Rubber Products(特种橡胶制品), 2022, 43(1): 1. [本文引用:1]
[12] ZHAO Qian, LIN Yuan-hua, WANG Qi, et al(赵倩, 林元华, 王奇, 等). New Technology & New Process(新技术新工艺), 2021, (8): 71. [本文引用:1]
[13] Xu L, Hu K, Chen D, et al. Accelerated Aging Test and Life Prediction of Rubber Strip for Connector Sealing: 3rd International Conference on System Reliability and Safoty Engineering (SRSE), 2021. 187. [本文引用:1]
[14] YUAN Zhao-kui, WU Tian-hao, LI Nan, et al(袁兆奎, 吴天昊, 李楠, 等). China Rubber/Plastics Technology and Equipment(橡塑技术与装备), 2019, 45(15): 42. [本文引用:1]
[15] MIAO Shu-guang, SHAO Dan, LIU Zhong-yu, et al(苗曙光, 邵丹, 刘忠育, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(6): 1755. [本文引用:1]
[16] Zhong Shuncong. Frontiers of Mechanical Engineering, 2019, 14(3): 273. [本文引用:1]
[17] Park Hochong, Son JooHiuk. Sensors, 2021, 21(4): 1186. [本文引用:1]
[18] HE Yu-han, ZHANG Yu-xin, ZHANG Zhen, et al(贺玉函, 张雨昕, 张震, 等). Synthetic Materials Aging and Application(合成材料老化与应用), 2020, 49(6): 126. [本文引用:1]
[19] GUO Qin-rui, SHAO Hua-feng(国钦瑞, 邵华锋). Chinese Polymer Bulletin(高分子通报), 2022, (2): 17. [本文引用:1]
[20] LIU Xuan, YANG Rui(刘璇, 杨睿). Materials for Mechanical Engineering(机械工程材料), 2020, 44(9): 1. [本文引用:1]
[21] ZHOU Kun, HU Bin, WANG Jin-mei, et al(周堃, 胡滨, 王津梅, 等). Equipment Environmental Engineering(装备环境工程), 2011, 8(4): 1. [本文引用:1]
[22] TIAN Zhou-ling(田周玲). Paper and Paper Making(纸和造纸), 2021, 40(3): 19. [本文引用:1]