高气压下三维旋转滑动弧放电光谱特性分析

引用本文

张磊, 张登成, 于锦禄, 赵兵兵, 徐哲霖, 程伟达. 高气压下三维旋转滑动弧放电光谱特性分析[J]. 光谱学与光谱分析, 2024,44(6): 1571-1577.
ZHANG Lei, ZHANG Deng-cheng, YU Jin-lu, ZHAO Bing-bing, XU Zhe-lin, CHENG Wei-da. Study of the Spectral Characteristics of 3D Rotating Gliding Arc Under High Pressure[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1571-1577.
Doi:10.3964/j.issn.1000-0593(2024)06-1571-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

高气压下三维旋转滑动弧放电光谱特性分析

张磊, 张登成, 于锦禄^*, 赵兵兵, 徐哲霖, 程伟达

中国人民解放军空军工程大学航空工程学院, 陕西西安 710038

*通讯作者 e-mail: smartaeroengine@163.com

作者简介: 张磊, 1996年生, 中国人民解放军空军工程大学航空工程学院博士研究生 e-mail: zhanglei1_dz@163.com

收稿日期: 2022-09-08 修回日期: 2023-10-24

基金: 国家自然科学基金项目(52276142, 51776223)资助

摘要

为探究气体压力对滑动弧放电稳定性的影响规律, 在高气压放电实验平台上, 开展了滑动弧放电光谱特性研究。利用发射光谱法对滑动弧放电过程中的激发态物质进行诊断, 并对不同气体压力条件下滑动弧放电的电子密度、振动温度、转动温度进行了计算。在滑动弧放电发射光谱中观测到氮气第二正带系N₂( C³ Π_u→ B³ Π_g)和氮气第一负带系N2+( B²Σu+→ X²Σg+)的发射谱线, 随着气体压力升高, 氮气第二正带系谱线发射强度增强, 氮气第一负带系的发射强度变化幅度较小。当气体压力超过0.26 MPa之后, 在滑动弧放电发射光谱中发现了氮气Gaydon's Green带系507.4 nm的发射谱线, 其发射强度为3 508.49 arb, 随气体压力升高其谱线发射强度无明显变化。利用Stark展宽法对滑动弧放电过程中的电子密度进行了计算, 得到电子密度在10²³量级, 并且随着气体压力的增加, 滑动弧放电的电子密度呈线性增加。针对氮气分子第二正带系的5条谱线, 采用玻尔兹曼图解法对滑动弧放电的振动温度进行计算, 振动温度随气体压力的变化并非单调变化, 在0.3 MPa之前振动温度变化幅度较小, 气体压力超过0.3 MPa之后振动温度迅速增加。对氮气分子第一负带系390~391.6 nm处的发射谱线进行拟合计算滑动弧放电的转动温度, 结果表明在0.24 MPa之前转动温度随气体压力升高变化幅度较大, 气体压力超过0.24 MPa之后转动温度增长幅度变小。

关键词: 滑动弧等离子体; 高气压放电; 电子密度; 振动温度; 转动温度

中图分类号:O433.4 文献标志码:A

Study of the Spectral Characteristics of 3D Rotating Gliding Arc Under High Pressure

ZHANG Lei, ZHANG Deng-cheng, YU Jin-lu^*, ZHAO Bing-bing, XU Zhe-lin, CHENG Wei-da

School of Aeronautical Engineering, Air Force Engineering University, Xi'an 710038, China

*Corresponding author

Abstract

To investigate the influence of gas pressure on the process of gliding arc discharge, the spectral characteristics of gliding arc discharge were studied on a high-pressure discharge experimental platform. The excited state substances in gliding arc discharge are diagnosed by emission spectroscopy,and the electron density, vibration temperature and rotation temperature of gliding arc discharge under different gas pressures are calculated. The emission lines of the second positive system of nitrogen N₂( C³ Π_u→ B³ Π_g) and the first negative system of nitrogenN2+( B²Σu+→ X²Σg+) are observed in the emission spectra of the gliding arc discharge. With the increase of gas pressure, the emission intensity of the emission line of the second positive system of nitrogen increases, whereas the emission intensity of the first negative system of nitrogen changes slightly. The Stark broadening method calculates the electron density in gliding arc discharge. It is found that the electron density is 10²³ orders of magnitude, and the electron density increases linearly with the increase of gas pressure. The vibration temperature of sliding arc discharge is calculated using the Boltzmann diagram method for the five spectral lines of the second positive system of nitrogen molecules. The change of vibration temperature with gas pressure is not monotone. The range of vibration temperature changes is small before 0.3 MPa and increases rapidly after the gas pressure exceeds 0.3 MPa. The rotational temperature of the discharge from the gliding arc was calculated by fitting the emission lines at 390~391.6 nm in the first negative nitrogen molecules system. The rotational temperature changed significantly with the increase of gas pressure before 0.24 MPa, and the addition of rotational temperature decreased when the gas pressure exceeded 0.24 MPa.

Keyword: Gliding arc plasma; High air pressure discharge; Electron density; Vibration temperature; Rotation temperature

文章图片

引言

滑动弧放电作为产生等离子体的重要方法, 因其结构简单、成本低^[1]、活性粒子密度大、化学选择性强^[2]等优点, 被广泛应用于强化燃烧^{[3, 4]}、燃料重整和污染物降解等领域^{[5, 6]}。在滑动弧放电过程中, 两电极间充满了包含激发态分子、原子、自由基等物质的气体, 这些激发态粒子在强电场的作用下频繁发生碰撞并向较低的能级跃迁, 在跃迁过程中就会以光的形式将多余的能量释放出去, 进而产生了发射光谱(optical emission spectrum, OES)^[7]。发射光谱诊断法作为一种无干扰式测量手段, 是等离子体技术领域的标准工具, 常被用来测量等离子体的各种性质。

由于激发态粒子的能级不同, 所以发射谱线所对应的粒子也是唯一的, 通过对发射光谱谱线的分析可以得到活性物质的种类与分布等信息, 因此专家学者对滑动弧放电的发射光谱开展了大量的研究工作。在光谱特征分析方面, Deng等^[8]设计了一种适用于航空发动机的滑动弧强化燃烧结构, 并分析了温度变化对滑动弧放电光谱特性的影响规律。雷建平^[9]等研究了空气流量、放电电压等工作参数对OH、 O原子等活性粒子发射强度的影响规律。 Yusuke等^[10]在重复脉冲放电条件下发现滑动电弧放电的发射光中存在激发的OH和NH等活性物质, 且通过分析发现OH的发射占主导地位。以上研究为发射光谱中谱线的辨认提供了一定的依据。在等离子体放电的特征温度计算方面, 刘志杰等^[11]总结了利用发射光谱计算等离子体特征温度特性的方法。冯博文等^[12]采用Stark展宽法和图像法计算了等离子体放电过程中电子密度, 曾鑫等^[13]综述了等离子体电子密度计算方法, 并基于Stark展宽原理开发了等离子体电子密度分析程序。 Ananthanarasimhan等^[14]利用发射光谱分析了湍流对电子温度的影响, 发现空气流量从5 SLPM增大到50 SLPM后, 电子温度从0.84 eV升高到2.2 eV。此外, 田裕等^[15]对预燃式等离子体射流点火器工作过程中的活性粒子进行了分析, 并计算了CN粒子的振动温度。以上利用发射光谱法对滑动弧放电过程的研究, 为滑动弧放电发射光谱中谱线的辨认、特征温度的分析提供了借鉴。

高气压下滑动弧放电是等离子体放电领域的难点, 也是关系到滑动弧工程化应用的重点, 目前, 关于高气压下滑动弧放电的光谱分析鲜有报道。本工作针对高气压下滑动弧放电的光谱特性进行研究, 利用发射光谱法对滑动弧放电的激发态物质进行诊断, 并计算了滑动弧放电过程中的电子密度、振动温度、转动温度。

1 实验部分

高气压滑动弧放电实验装置如图1所示。实验过程中滑动弧等离子体激励器安装在高气压实验舱体(直径0.8 m, 长1.5 m)进气口尾端, 通过调节高压实验舱体的进气流量和排气流量, 保证驱动滑动弧旋转的空气流量和高气压放电所需的环境压力。螺杆式空气压缩机(最大排气压力0.8 MPa)通过管路与高气压实验舱体的进气口连接, 为实验提供所需压力和空气流量, 进气流量设置为0.043 5 kg· s^-1。滑动弧等离子体激励器的具体结构在文献[1]中有详细的介绍, 两电极间最小间隙为10.9 mm。滑动弧等离子体激励器的高压线缆通过高压舱体的绝缘接线柱与激励电源相连接, 滑动弧等离子体放电激励电源为CG-10000FG型等离子体电源, 为保证实验工况下滑动弧放电成功, 电源的调制频率设置为17 kHz。

	Figure Option View Download New Window
	图1 实验系统示意图Fig.1 Schematic diagram of experimental system

滑动弧放电过程的发射光谱由AvaSpec-ULS2048型四通道光谱仪采集。光纤探头设置在高气压实验舱体光学玻璃观察窗口的外侧, 与放电区域呈垂直状, 距离滑动弧放电区域13 mm。 200~900 nm范围内的光谱信号被采集后由计算机完成数据的记录和处理。

2 结果与讨论

2.1 发射光谱分析

大气压下滑动弧放电发射光谱如图2(a)所示, 发射光谱集中在320~600 nm范围内, 图2(b)为图2(a)在355~389 nm范围内的放大图。在大气压下滑动弧放电发射光谱中, 发现了氮气第二正带系N₂(C³Π _u→ B³Π _g)包含波长为337.1 nm(N₂(2+), (0, 0))、 353.6 nm(N₂(2+), (1, 2))、 357.6 nm(N₂(2+), (0, 1))、 370.9 nm(N₂(2+), (2, 4))、 375.4 nm(N₂(2+), (1, 3))、 380.4 nm(N₂(2+), (0, 2))、 405.8 nm(N₂(2+), (0, 3))的发射谱线; 氮气第一负带系 $N_{2}^{+}$ (B² $Σ_{u}^{+}$ → X² $Σ_{g}^{+}$ )包含波长为356.1 nm( $N_{2}^{+}$ (1-), (2, 1))、 358.0 nm( $N_{2}^{+}$ (1-), (1, 0))、 388.2 nm( $N_{2}^{+}$ (1-), (1, 1))、 391.1 nm( $N_{2}^{+}$ (1-), (0, 0))、 419.7 nm( $N_{2}^{+}$ (1-), (2, 3))、 423.4 nm( $N_{2}^{+}$ (1-), (1, 2))、 427.5 nm( $N_{2}^{+}$ (1-), (0, 1))的发射谱线^[16]。图2(c)是气体压力为0.26 MPa时500~550 nm范围内的发射光谱; 分析发现当气体压力超过0.26 MPa后, 会在发射光谱中发现氮气的Gaydon's Green带系的507.4 nm谱线, 发射强度为3 508.49 arb, 这是N₂(H³Φ _u)向N₂(G³Δ _g)跃迁时产生的^[17], 其发射强度随气体压力变化无明显变化。

	Figure Option View Download New Window
	图2 滑动弧放电发射光谱Fig.2 Gliding arc discharge emission spectrum

选取氮气第二正带系405.8和367.0 nm的发射谱线以及氮气第一负带系388.2和419.7 nm的发射谱线, 探究气体压力对氮气激发态的影响规律。由图3可知, 气体压力升高, 氮气第二正带系N₂(C³Π _u→ B³Π _g)两条谱线的发射强度增强, 这是由于N₂(C³Π _u→ B³Π _g)主要由式(1)和式(2)反应产生

$e + N_{2} (X^{1} Σ_{g}^{+}) \to N_{2} (C^{3} Π_{u}) + e, Δ e = 13.06 eV$ (1)

$N_{2} (C^{3} Π_{u}) \to N_{2} (B^{3} Π_{g}) + hν$ (2)

随着气体压力的升高, 阴极发射出的高能电子数量增多, 电子的碰撞促进了N₂(C³Π _u→ B³Π _g)的生成, 因此发射强度升高。而氮气第一负带系 $N_{2}^{+}$ (B² $Σ_{u}^{+}$ → X² $Σ_{g}^{+}$ )的两条谱线随气体压力升高幅度变化不大, 气体压力从0.1 MPa升高至0.38 MPa, 419.7 nm处的谱线强度仅增加458.29 arb。 $N_{2}^{+}$ (B² $Σ_{u}^{+}$ → X² $Σ_{g}^{+}$ )主要由以下反应产生

$e + N_{2} (X^{1} Σ_{g}^{+}) \to N_{2} (B^{2} Σ_{u}^{+}) + 2 e, Δ e = 18.76 eV$ (3)

$e + N_{2}^{+} (X^{2} Σ_{g}^{+}) \to N_{2}^{+} (B^{2} Σ_{u}^{+}) + e, Δ e = 3.13 eV$ (4)

$N_{2}^{+} (B^{2} Σ_{u}^{+}) \to N_{2}^{+} (X^{2} Σ_{g}^{+})$ (5)

由式(1)和式(3)可知, 同为初始反应, 高能电子在激发氮气产生N₂(C³Π _u)和N₂(B² $Σ_{u}^{+}$ )时, 产生N₂(C³Π _u)所需的电子能更少, 因此更有利于N₂(C³Π _u→ B³Π _g)的生成。此外由式(4)和式(5)可知, $N_{2}^{+}$ (X² $Σ_{g}^{+}$ )既是中间产物也是终端生成产物, 且式(4)所需的电子能量仅为3.13 eV, 因此其消耗远大于其生成, 以上两方面原因导致氮气分子第二正带系N₂(C³Π _u→ B³Π _g)发射强度增加, 而氮气分子第一负带系 $N_{2}^{+}$ (B² $Σ_{u}^{+}$ → X² $Σ_{g}^{+}$ )发射强度增长幅度小甚至是略有减少。

	Figure Option View Download New Window
	图3 气体压力对氮气激发态发射强度的影响Fig.3 Effect of gas pressure on emission intensity of nitrogen excited state

2.2 电子密度分析

电子密度作为评价等离子体的一个重要指标, 通常表征气体的电离程度, 可通过Stark展宽法求得。实验过程中测得的等离子体发射谱线并不是单纯的线型, 而是在中心波长λ ₀附近具有一定展宽和轮廓的谱线, 这种谱线为高斯线型和洛伦兹线型的共同函数, 称为Voigt线型。在谱线的加宽机制中Vander Waals展宽(Δ λ _van)、 Stark展宽(Δ λ _Stark)为洛伦兹线型, 多普勒展宽(Δ λ _Doppler)和仪器展宽(Δ λ _Instrument)为高斯线型, 其中洛伦兹线型的半高全宽可以表示为

$Δ λ_{Lorentz} = Δ λ_{Stark} + Δ λ_{van}$ (6)

高斯线型的半高全宽表示为

$Δ λ_{Gauss} = \sqrt[]{Δ λ_{Doppler}^{2} + Δ λ_{Instrument}^{2}}$ (7)

式(7)中仪器展宽(Δ λ _Instrument)由仪器本身决定, 而多普勒展宽(Δ λ _Doppler)又可表示为

$Δ λ_{Doppler} = 2 \times 3.0414 \times 10^{- 7} \sqrt[]{\frac{T}{A}} λ_{0}$ (8)

式(8)中, T为气体温度, 近似等于转动温度T_rot, A为气体分子量, λ ₀为发射谱线中心波长。

因实验中观测到的谱线为Voigt线型, 可以表示为高斯函数和洛伦兹函数的卷积形式

$Φ_{v} (ω, Γ, δ) d ω = d ω \overset{+ \infty}{\int_{- \infty}} d ω^{' Φ_{L}} (ω^{'}, Γ) Φ_{G} (ω - ω^{'}, δ)$ (9)

Φ _v(ω , Γ , δ )、 Φ _L(ω ', Γ )、 Φ _G(ω -ω ', δ )分别表示Voigt、洛伦兹、高斯线性函数。根据2.4节中的转动温度可以求出多普勒展宽(Δ λ _Doppler), 通过反卷积可以解出洛伦兹展宽(Δ λ _Lorentz)的值, 然后减去Vander Waals展宽(Δ λ _van)就可得出Stark展宽(Δ λ _Stark)的值。非氢原子的Stark展宽(Δ λ _Stark)与电子密度存在如式(10)关系

$\begin{array}{l} Δ λ_{Stark} = 2 \times [1 + 1.75 \times 10^{- 4} \times N_{e}^{1 / 4} α \times \\ (1 - 0.068 N_{e}^{1 / 6} T_{e}^{- 1 / 2})] \times 10^{- 16} ω N_{e} \end{array}$ (10)

式(10)中, α 为离子碰撞展宽系数, ω 为电子碰撞展宽系数, 二者均为电子温度的函数, N_e为电子密度。通过此式求得电子密度随气压变化规律如图4所示。

	Figure Option View Download New Window
	图4 气体压力对电子密度的影响Fig.4 Effect of gas pressure on electron density

由图4可知, 滑动弧等离子体放电的电子密度整体保持在10²³量级, 这表明滑动弧放电达到局部热力学平衡, 这与滑动弧放电的客观事实相吻合。滑动弧放电的电子密度随着气体压力的升高呈线性增长, 这是因为随着气体压力的升高, 单位体积内的气体分子数量增多, 同时滑动弧放电的功率增大, 单位时间内注入到两电极间的能量增多, 使得更多的气体分子被电离, 因此电子密度增加。依据N_e=I/μ _eeS(式中N_e为电子密度, I为电流, μ _e为电子迁移率, S为放电截面积)可知, 在电极结构不变的情况下, 电子密度与电流呈正相关, 随着气体压力的升高, 电弧击穿时刻的电流和维持电弧发展的电流都变大^[1], 进而验证了电子密度增大趋势。

2.3 振动温度分析

振动温度是表征非平衡态等离子体振动激发强度的重要参数。选用氮分子第二正带系N₂(C³Π _u→ B³Π _g)的5条发射谱线进行分析, 并采用玻尔兹曼图解法计算其振动温度。

双原子分子发射光谱振动谱带的谱线强度为

$I_{v^{'} v^{″}} = hc ν_{v^{'} v^{″}} p_{v^{'} v^{″}} N_{v^{'}}$ (11)

式(11)中, h为普朗克常数(h=6.626 069 75× 10^-34 J· s), c为光速(c=3× 10⁸ m· s^-1), ν _v'v″为发射光谱线频率, p_v'v″为上、下两能级之间的跃迁几率, N_v'为上态分子布居数, v'、 v″分别为上态、下态振动量子数。

由分子光谱学理论可知, 上态振动能量为

$E_{v'} = ω_{e} (v' + \frac{1}{2}) - ω_{e} x_{e} {(v' + \frac{1}{2})}^{2} + ω_{e} y_{e} {(v' + \frac{1}{2})}^{3} + \dots$ (12)

式(12)中, 等号右端第三项及后面各项与前两项相比小得多, 计算中可以忽略不计。

当等离子体处于局部热平衡状态时, 上态分子布居数符合玻尔兹曼分布, 并满足如式(13)关系

$N_{v^{'}} = N_{0} e^{- \frac{E_{v^{'}}}{k T_{vib}}}$ (13)

联立式(11)、式(12)和式(13)式得到

$\ln \frac{I_{v'v″}}{v_{v'v″} p_{v'v″}} = C - \frac{E_{v'}}{k T_{vib}}$ (14)

式(14)中, T_vib为振动温度, C为常数, k=8.617 689× 10^-5 eV· K^-1。令B=I_v'v″/v_v'v″p_v'v″, 以lnB作为因变量, 振动能量E_v'作为自变量, 求出直线的斜率, 进而求得转动温度T_vib。求解过程所需数据列于表1[NIST]。图5为大气压条件下玻尔兹曼图解法拟合过程, 从图中可以看出拟合程度较高。

表1 氮分子第二正带系N₂(C³Π _u→ B³Π _g)的波长和跃迁几率 Table 1 Wavelength and transition probability of the second positive band system N₂(C³Π _u→ B³Π _g) of nitrogen molecule

	Figure Option View Download New Window
	图5 直线斜率拟合过程Fig.5 Straight line slope fitting process

振动温度随气体压力变化规律如图6所示, 当气体压力从0.1 MPa升高到0.38 MPa时, 振动温度从4 280 K升高到7 906 K。分子的振动能级是由高能电子的冲击激发的, 以氮气分子为例, 高振动态氮气分子N₂(C³Π _u)主要是基态N₂分子和低能级N₂(A³ $Σ_{u}^{+}$ )发生电子碰撞激发、关联激发、合并反应等过程产生^[7], 主要反应有

$N_{2} (X^{1} Σ_{g}^{+}) + e \to N_{2} (C^{3} Π_{u})$ (15)

$N_{2} (X^{1} Σ_{g}^{+}) + e \to N_{2} (A^{3} Σ_{u}^{+})$ (16)

$N_{2} (A^{3} Σ_{u}^{+}) + N_{2} (A^{3} Σ_{u}^{+}) \to N_{2} (C^{3} Π_{u})$ (17)

由2.2节可知, 随着气体压力的升高, 注入到两电极之间的能量增多, 因此分子之间碰撞、离解产生了更多的电子, 这有利于高振动态能级N₂(C³Π _u)的产生, 使得振动温度升高。另一方面根据mv²/2=eEλ (式中λ , m和e分别为电子平均自由程、电子质量和电子电荷量, E为场强)可知, 电子获得的能量主要由电场强度和电子平均自由程决定, 在高气压下, 电子碰撞概率增加, 电子平均自由程变小, 电子获得的能量主要由两电极间的场强决定。随着气体压力升高, 电场强度增大, 平均电子能量增大, 使得振动温度升高。这也意味着更多的能量被储存在高振动态分子中, 同时意味着随着气体压力的升高, 等离子体的化学活性增强。

由图6分析可知, 当气体压力超高0.3 MPa时, 振动温度升高的幅度变大。根据振动态粒子相对数量关系式R=N_v/N_g=N_ek_v(T_e)(式中N_v为振动态粒子密度, N_e为电子密度, N_g为粒子基态密度, k_v为振动激发反应速率常数, 是电子温度T_e的函数)可知振动态粒子数量与电子密度和电子温度呈正相关, 气体压力升高, 电子密度增加, 且气体压力超过0.3 MPa之后电子激发温度增长幅度变大^[1], 进而使得振动温度升高的幅度变大。

	Figure Option View Download New Window
	图6 气体压力对振动温度的影响Fig.6 Influence of gas pressure on vibration temperature

2.4 转动温度分析

转动温度是等离子体温度中的一个重要参数, 表征等离子体中转动自由度的能量。由于转动温度与平动温度能量平衡时间较短, 很快能够达成平衡状态, 而且分子的不同转动能级间的间隙远小于振动能级的间隙, 因此可以将转动温度近似看作气体温度。通过研究转动温度, 可以分析放电区域气体温度的变化规律。

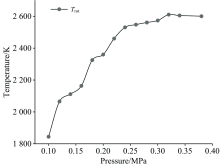
对氮的第一负带系390~391.6 nm处的发射谱线, 在Lifbase软件(http://www.sri.com/psd/lifbase/)中进行拟合。当转动温度为1 844 K时, 拟合得到的谱线与实验测得的数据吻合度较高, 则认为此时的转动温度为1 844 K。通过拟合获得不同气压下等离子体转动温度如图7所示。分析可知, 随着气体压力的升高, 转动温度整体呈升高趋势, 由气体放电的帕邢定律V_s_min=B(pl)_min(式中V_smin为最小击穿电压, B为汤森电离系数, p为气体压力, l为极间距)可知放电电压随着气体压力的升高而增大, 在极间距不变的情况下, 两电极间的场强增强, 阴极发射的电子会在电场中获得更高的能量, 电子与基态氮气分子碰撞生成高激发态氮气分子, 电子能量越高此过程进行的越激烈, 进而使得分子高转动能态布居数增多, 使得转动温度升高。气体压力从0.1 MPa升高到0.24 MPa时转动温度从1 844 K升高到2 530 K, 增长了686 K, 但是气体压力超过0.24 MPa之后, 转动温度增长幅度变小, 当气体压力达到0.38 MPa时, 转动温度仅增加70 K, 这与振动温度增长幅度变化相反。这与文献[1]中, 能量变化趋势相吻合, 气体压力超过0.24 MPa之后, 滑动弧放电的能量增幅变小, 因此注入到电极间的能量与并没有特别大的增长, 高能电子中的能量被更多的储存在高振动态分子中^[14], 使得振动温度显著升高, 而转动温度增长幅度变小。

	Figure Option View Download New Window
	图7 气体压力对转动温度的影响Fig.7 Effect of gas pressure on rotating temperature

对比图6和图7发现等离子体的振动温度(T_vib)大于转动温度(T_rot), 这表明更多的能量通过振动激发参与电化学过程, 而不是完全用于非选择性加热所有气体, 这表明高气压下滑动弧放电具有更好的化学选择性。经过计算滑动弧放电的转动温度高于其他形式的等离子体放电的转动温度, 受气体温度的影响, 高气压下滑动弧放电具有更高的化学反应速率。

3 结论

(1)滑动弧放电发射光谱主要集中在330~600 nm范围内, 在滑动弧放电发射光谱中发现了氮气第二正带系N₂(C³Π _u→ B³Π _g)和氮气第一负带系 $N_{2}^{+}$ (B² $Σ_{u}^{+}$ → X² $Σ_{g}^{+}$ )的发射谱线; 随着气体压力升高, 氮气第二正带系谱线发射强度大幅度增加, 氮气第一负带系的发射强度变化较小。当气体压力超过0.26 MPa之后, 在滑动弧放电发射光谱中发现了氮气Gaydon's Green带系507.4 nm的发射谱线。

(2)利用Stark展宽法对滑动弧放电过程中的电子密度进行了计算, 得到电子密度在10²³量级, 这表明滑动弧放电达到局部热力学平衡; 随着气体压力的升高, 滑动弧放电的电子密度呈线性增加。

(3)采用玻尔兹曼图解法对滑动弧放电的振动温度进行计算, 采用谱线拟合法, 得到滑动弧放电的转动温度, 两者随气体压力升高的增长幅度相反; 振动温度大于转动温度, 滑动弧放电具有更好的化学选择性。

参考文献

文献列表

[1]	ZHANG Lei, YU Jin-lu, ZHAO Bing-bing, et al(张磊, 于锦禄, 赵兵兵, 等). Acta Physica Sinica(物理学报), 2022, 71(7): 075204. [本文引用:5]
[2]	YU Jin-lu, ZHAO Bing-bing, GUO Hao, et al(于锦禄, 赵兵兵, 郭昊, 等). Aeroengine(航空发动机), 2022, 48(3): 52. [本文引用:1]
[3]	ZHANG Lei, YU Jin-lu, CHEN Yi, et al(张磊, 于锦禄, 陈一, 等). Acta Aeronautica et Astronautica Sinica(航空学报), 2021, 42(3): 124308. [本文引用:1]
[4]	Zhang Lei, Zhang Dengcheng, Yu Jinlu, et al. Plasma Science and Technology, 2023, 25(3): 035502. [本文引用:1]
[5]	Jennifer Martin-del-Campo, Marianna Uceda, Sylvain Coulombe, et al. Journal of CO₂ Utilization, 2021, 46: 101474. [本文引用:1]
[6]	Kong Xiangzhi, Wu Angjian, Fu Siming, et al. Fuel, 2021, 298: 120745. [本文引用:1]
[7]	HE Li-ming, YU Jin-lu, ZENG Hao (何立明, 于锦禄, 曾昊). The Technology of Plasma Ignition and Assisted Combustion(等离子体点火与助燃技术), Beijing: Aviation Industry Press北京: 航空工业出版社, 2019. [本文引用:2]
[8]	Deng Jun, Cui Gang, Lu Yongji, et al. Vacuum, 2023, 207: 111621. [本文引用:1]
[9]	LEI Jian-ping, HE Li-ming, CHEN Yi, et al(雷建平, 何立明, 陈一, 等). Acta Physica Sinica(物理学报), 2020, 69(19): 195203. [本文引用:1]
[10]	Yusuke Kikuchi, Tsubase Nakagawa. IEEE Transactions on Plasma Science, 2021, 49(1): 4. [本文引用:1]
[11]	LIU Zhi-jie, CHEN Min, LIU Ding-xin(刘志杰, 陈旻, 刘定新). High Voltage Engineering(高电压技术), 2022, 48(10): 4196. [本文引用:1]
[12]	FENG Bo-wen, WANG Ruo-yu, MA Yu-peng-xue, et al (冯博文, 王若愚, 马雨彭雪), 等). Acta Physica Sinica(物理学报), 2021, 70(9): 095201. [本文引用:1]
[13]	ZENG Xin, ZHANG Shuai, BAI Han, et al (曾鑫, 张帅, 白晗), 等). Proceedings of the Chinese Society for Electrical Engineering (中国电机工程学报), 2023, doi: DOI:10.13334/j.0258-8013.pcsee.230256. [本文引用:1]
[14]	Ananthanarasimhan J, Rao Lakshminarayana. Journal of Physics D: Applied Physics, 2022, 55: 245202. [本文引用:2]
[15]	TIAN Yu, YU Jin-lu, JIANG Yong-jian, et al(田裕, 于锦禄, 蒋永健, 等). Journal of Combustion Science and Technology(燃烧科学与技术), 2021, 27(5): 562. [本文引用:1]
[16]	David Staack, Bakhtier Farouk, Alexand er Gutsol, et al. Plasma Sources Science and Technology, 2005, 14(4): 700. [本文引用:1]
[17]	SHEN Li-hua, YU Chun-xia, YAN Bei, et al(申丽华, 于春侠, 闫蓓, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(3): 791. [本文引用:1]

2022

0.0

... 引言滑动弧放电作为产生等离子体的重要方法, 因其结构简单、成本低^[1]、活性粒子密度大、化学选择性强^[2]等优点, 被广泛应用于强化燃烧^[3,4]、燃料重整和污染物降解等领域^[5,6] ...

... 滑动弧等离子体激励器的具体结构在文献[1]中有详细的介绍, 两电极间最小间隙为10 ...

... _e为电子迁移率, S为放电截面积)可知, 在电极结构不变的情况下, 电子密度与电流呈正相关, 随着气体压力的升高, 电弧击穿时刻的电流和维持电弧发展的电流都变大^[1], 进而验证了电子密度增大趋势 ...

... 3 MPa之后电子激发温度增长幅度变大^[1], 进而使得振动温度升高的幅度变大 ...

... 这与文献[1]中, 能量变化趋势相吻合, 气体压力超过0 ...

2022

0.0

2021

0.0

2023

0.0

2021

0.0

2021

0.0

... 在滑动弧放电过程中, 两电极间充满了包含激发态分子、原子、自由基等物质的气体, 这些激发态粒子在强电场的作用下频繁发生碰撞并向较低的能级跃迁, 在跃迁过程中就会以光的形式将多余的能量释放出去, 进而产生了发射光谱(optical emission spectrum, OES)^[7] ...

... _u)主要是基态N₂分子和低能级N₂(A³Σu+)发生电子碰撞激发、关联激发、合并反应等过程产生^[7], 主要反应有 ...

2023

0.0

... 在光谱特征分析方面, Deng等^[8]设计了一种适用于航空发动机的滑动弧强化燃烧结构, 并分析了温度变化对滑动弧放电光谱特性的影响规律 ...

2020

0.0

... 雷建平^[9]等研究了空气流量、放电电压等工作参数对OH、 O原子等活性粒子发射强度的影响规律 ...

2021

0.0

... Yusuke等^[10]在重复脉冲放电条件下发现滑动电弧放电的发射光中存在激发的OH和NH等活性物质, 且通过分析发现OH的发射占主导地位 ...

2022

0.0

... 在等离子体放电的特征温度计算方面, 刘志杰等^[11]总结了利用发射光谱计算等离子体特征温度特性的方法 ...

2021

0.0

... 冯博文等^[12]采用Stark展宽法和图像法计算了等离子体放电过程中电子密度, 曾鑫等^[13]综述了等离子体电子密度计算方法, 并基于Stark展宽原理开发了等离子体电子密度分析程序 ...

0.0

2022

0.0

... Ananthanarasimhan等^[14]利用发射光谱分析了湍流对电子温度的影响, 发现空气流量从5 SLPM增大到50 SLPM后, 电子温度从0 ...

... 24 MPa之后, 滑动弧放电的能量增幅变小, 因此注入到电极间的能量与并没有特别大的增长, 高能电子中的能量被更多的储存在高振动态分子中^[14], 使得振动温度显著升高, 而转动温度增长幅度变小 ...

2021

0.0

... 此外, 田裕等^[15]对预燃式等离子体射流点火器工作过程中的活性粒子进行了分析, 并计算了CN粒子的振动温度 ...

2005

0.0

... 5 nm( N2+(1-), (0, 1))的发射谱线^[16] ...

2015

0.0

... _g)跃迁时产生的^[17], 其发射强度随气体压力变化无明显变化 ...