引用本文
曾庆栋, 陈光辉, 李文鑫, 孟久灵, 李耿, 童巨红, 田志辉, 张晓林, 李国辉, 郭连波, 肖永军. 基于粒子群-支持向量机算法的激光诱导击穿光谱钢铁快速检测与分类[J]. 光谱学与光谱分析, 2024,44(6): 1559-1565.
ZENG Qing-dong, CHEN Guang-hui, LI Wen-xin, MENG Jiu-ling, LI Geng, TONG Ju-hong, TIAN Zhi-hui, ZHANG Xiao-lin, LI Guo-hui, GUO Lian-bo, XIAO Yong-jun. Classification of Special Steel Based on LIBS Combined With Particle Swarm Optimization and Support Vector Machine[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1559-1565.
Doi:10.3964/j.issn.1000-0593(2024)06-1559-07  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于粒子群-支持向量机算法的激光诱导击穿光谱钢铁快速检测与分类
曾庆栋1,2, 陈光辉1,3, 李文鑫1, 孟久灵1, 李耿1, 童巨红1, 田志辉1, 张晓林1, 李国辉1, 郭连波2, 肖永军1,*
1. 湖北工程学院物理与电子信息工程学院, 湖北 孝感 432000
2. 华中科技大学武汉光电国家研究中心, 湖北 武汉 430074
3. 湖北大学物理与电子科学学院, 湖北 武汉 430062
*通讯作者 e-mail: 346917126@qq.com

作者简介: 曾庆栋, 1982年生, 湖北工程学院物理与电子信息工程学院教授 e-mail: jerry-z@hbeu.edu.cn

收稿日期: 2022-07-23 修回日期: 2023-12-13
基金: 国家自然科学基金项目(61705064), 湖北省自然科学基金项目(2021CFB607), 湖北省教育厅团队研究项目(T201617), 孝感市自然科学计划项目(XGKJ2021010003)资助
摘要

钢铁是国民经济中的支柱性产业, 由于受生产技术的限制, 我国钢铁产品主要集中为质量参差不齐的中低端产品, 废品率较高, 易造成资源浪费和环境污染。 因此, 钢铁产品的快速检测与鉴别分类, 对保护环境以及提高钢铁资源的回收利用率有着重要意义。 利用激光诱导击穿光谱技术(LIBS)进行10种钢铁样品光谱数据的快速采集, 并采用支持向量机(SVM)算法对其数据进行学习建模, 得到钢铁快速分类模型。 然而, 由于不同钢铁样品的光谱数据特征是复杂且相似的, 导致设置的模型参数也会对SVM模型的分类结果有着较大的影响。 为了实现对不同牌号钢铁合金的快速检测分类, 实验中采用粒子群算法(PSO)与网格寻优法两种不同方法来优化模型参数, 并分别选取样品中6种微量元素(Mn、 Cr、 Cu、 V、 Mo、 Ti)的17条特征谱线, 和经主成分分析法(PCA)对全谱数据降维提取得到的前17个主成分作为模型的输入, 建立PSO-SVM、 PSO-PCA-SVM、 PCA-SVM和SVM四种分类模型。 实验结果表明, 相比于精度最高的PCA-SVM模型的优化时间(257.84 s), PSO-SVM模型优化时间最短(11.5 s), 且识别精度可达96.67%, 与PCA-SVM模型的精度(97.5%)几乎相当。 该结果表明LIBS结合PSO-SVM算法可实现快速的钢铁检测与分类, 该方法为钢铁产品的快速检测与分类提供了一种新的解决途径。

关键词: 激光诱导击穿光谱; 支持向量机; 粒子群算法; 钢铁分类
中图分类号:O433.4 文献标志码:A
Classification of Special Steel Based on LIBS Combined With Particle Swarm Optimization and Support Vector Machine
ZENG Qing-dong1,2, CHEN Guang-hui1,3, LI Wen-xin1, MENG Jiu-ling1, LI Geng1, TONG Ju-hong1, TIAN Zhi-hui1, ZHANG Xiao-lin1, LI Guo-hui1, GUO Lian-bo2, XIAO Yong-jun1,*
1. School of Physics and Electronic Information Engineering, Hubei Engineering University, Xiaogan 432000, China
2. Wuhan National Laboratory for Optoelectronics (WNLO), Huazhong University of Science and Technology, Wuhan 430074, China
3. Faculty of Physics and Electronic Science, Hubei University, Wuhan 430062, China
*Corresponding author
Abstract

The steel industry has become a mainstay of the Chinese national economy. Due to the limitation of production technology, Chinese steel products are mainly concentrated in the middle and low-end products of uneven quality. It could result in the severe waste of steel resources and the pollutionofmetal garbage wastes. Therefore, the rapid identification and classification method of steel products is significant for environmental protection and for improving steel resources' recycling rate. This work utilised laser-induced breakdown spectroscopy (LIBS) to quickly collect the spectral data of 10 kinds of special steels. Then, a support vector machine (SVM) learned and modelled the spectral data to obtain the rapid steel classification model. However, due to the element composition of different special steels being complex and similar, the performance of classification results may be directly and significantly affected by SVM model parameters. To realise the rapid classification and detection of different grades of steel alloys, the two different methods of particle swarm optimisation (PSO) and grid search optimization were used to optimize the model parameters and speed up the training efficiency. Then, the spectral intensity of 17 characteristic lines of 6 major trace elements (Mn, Cr, Cu, V, Mo and Ti) in samples and 17 feature information variables extracted from the LIBS spectrum data with full variables by principal component analysis (PCA) were chosen as the input to establish the PSO-SVM, PSO-PCA-SVM, PCA-SVM and SVM models for steel classification respectively. The experimental results show that compared with the SVM model's optimization time of 115.64 s, the shortest optimization time of PSO-SVM is 11.5 s, and its classification accuracy (96.67%) is not significantly inferior to the accuracy of the PCA-SVM model (97.5%). The results show that LIBS combined with the PSO-SVM algorithm can achieve rapid and high-precision steel classification, which provides a new solution to detect and classifythedifferent steel products rapidly and precisely.

Keyword: Laser-induced Breakdown spectroscopy; Support vector machine; Particle swarm optimization; Steel Classification
引言

钢铁所具有的独特的物理性能被广泛地应用于不同领域, 在现代社会发展中有着其他材料无法替代的重要作用, 是社会发展的核心产业。 由于受生产工艺的限制, 质量较差的中低端钢铁制品使用寿命较低, 有着较高的废品率, 导致了大量废弃钢铁制品的产生, 进而造成贵金属等不可再生资源的极大浪费。 由于不同种类的废钢包含了不同种类及含量的元素, 因此, 对废钢种类进行快速、 有效的分类识别是提高废钢资源回收利用率的关键所在。 然而, 传统的钢铁检测方法如X射线荧光光谱法、 电感耦合等离子体原子发射光谱法、 火花原子发射光谱法、 质谱法等在对钢铁成分进行分析时存在着各自的缺点和不足, 例如, 复杂的样品预处理、 检测成本高、 检测时间较长、 对实验者的专业知识要求较高以及只能在实验室环境下检测等缺点[1, 2, 3, 4]。 因此, 迫切需要一种可实时在线的对钢铁产品的品牌种类进行快速分类的方法。

激光诱导击穿光谱(laser induced breakdown spectroscopy, LIBS), 是一种对物质成分进行定性及定量分析的原子发射光谱技术[4], 通过对激光烧蚀物质产生的高温等离子体光谱进行采集及分析, 从而得到待测样品的物质成分及含量。 由于LIBS技术具有样品制备过程简单、 可远程非接触分析、 检测速度快、 可多元素同时分析等优点[5], 近年来已被广泛应用于工业冶金、 材料分析和生物医学等诸多领域[6, 7, 8]。 特别是通过与相关机器学习算法的结合, 该技术在物质的快速分类领域展现了广阔的应用前景。 例如, Gazeli等通过采用主成分分析法(principal component analysis, PCA)来剔除原始LIBS光谱数据中的大量无关变量, 从而提高分类模型的计算效率和分析精度, 以PCA降维提取的特征信息作为模型的输入变量, 并分别采用支持向量机(support vector machines, SVM)、 随机森林(random forest, RF)和线性判别分析法等不同算法来对其进行分析建模, 从而实现了对8种不同酸度的橄榄油样品的产地的快速分类检测, 其最高识别分类率可达99.2%[9]; Yelameli等测量了30块深海热液沉积岩的LIBS光谱数据, 将PCA与SVM、 人工神经网络(artificial neural network, ANN), k最近邻搜索(K nearest neighbor, KNN)等算法结合, 结果表明PCA-SVM方法的识别准确率达98%, 该方法为沉积岩类别的快速鉴别提供了新的方法[10]; Yao等采用遗传算法(genetic algorithm, GA)来对SVM分类模型的关键参数进行优化, GA-SVM模型对5种茶叶的识别准确率成功的从单纯使用SVM模型的87.46%提高到了98.4%, 该结果可为市场茶叶的快速分类提供新方法[11]; Shin等在类似金属样品的LIBS数据分类实验中, 证明了选择分析权重较高的相关元素的特征谱线作为LDA方法的输入, 可在保持精度的前提下大幅减少计算时间, 表明了合适的输入变量可以显著提高分类模型的建模效率[12]。 2020年, Kim等对LIBS光谱数据进行预处理分析后, 利用PLS-DA算法实现了对5类不同金属95.5%的高精度识别[13]。 2022年, Chen等采用优化后的深度信念网络算法对13类钢铁样品实现了100%的高精度识别分类[14]。 Wang等将PCA和ANN方法相结合, 通过PCA获得评分矩阵, 并建立了反向传播人工神经网络(BP-ANN)模型, 利用LIBS技术对不同产地或部位的三种中药材进行了分析和鉴定, 结果显示平均分类准确率为99.89%[15]。 Wang等还采用LIBS技术结合判别分析法(DA)对龙井等6种茶叶进行了分析鉴定, 茶叶的平均正确识别率为98%[16]。 Liu等利用高光谱成像(HSI)结合机器学习算法对生长在中国的六种米样品的进行了产地识别, LIBS和HSI数据融合识别的准确达到了99.85%[17]。 李明亮等对LIBS光谱进行三阶最小背景去除和小波阈值去噪, 再用多变量线性回归方法、 中高斯核支持向量机回归方法和归一化偏最小二乘法拟合回归方法, 建立了铝合金中铜元素的定量分析模型。 标准化PLSR模型对铝合金中Cu元素定量分析的精度和准确度均有显著提高, LIBS定标曲线的R2、 RMSEC、 RMSEP和ARE分别为0.997、 0.014 wt%、 0.129 wt%和3.053%[18]。 赵上勇等建立了LIBS与PCA算法相结合的模型, 用于人参的分类和重金属检测, 结果表明, 人参中铅和铬的检出限分别为9.55和10.86 mg· kg-1[19]。

上述研究结果表明, LIBS技术结合机器学习算法在对物质种类的快速分类问题上取得了较好的结果。 本文选用SVM作为分类算法来对钢铁样品的光谱数据进行分析研究。 然而, 由于输入变量的复杂度、 不同样品数据之间的相似度、 模型设置的惩罚参数C与核参数g等因素都会极大的影响SVM分类模型的精度与建模效率。 并且对于具有组成元素种类多、 含量较低等特点的钢铁样品来说, 由LIBS技术所探测到的不同样品的光谱数据, 其谱线分布及其光谱强度差异性较小, 不仅难以通过人工手段来鉴定样品的种类, 也增加了设置恰当SVM模型参数的难度。 因此在LIBS数据处理的过程中, 算法模型的性能往往受到参数的选择和调整的影响。 调整算法参数可以使得算法更好地适应数据集的特征, 提高模型的准确性和泛化能力, 通过合理优化参数, 可以进一步提高模型的预测能力和实际应用效果。

为了实现在工业现场快速对特钢样品牌号识别分类的目的, 本实验采用LIBS技术来快速获取光谱数据, 并对比了在不同输入变量下, 分别以网格寻优法和粒子群算法(particle swarm optimization, PSO)对SVM分类模型进行优化的实验结果。 该研究对钢铁的快速分类提供了一种新的解决途径。

1 实验部分
1.1 仪器

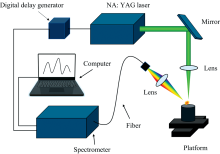
实验所采用的LIBS设备示意图如图1所示。 采用美国BigSky公司研发的Ultra系列的Nd∶ YAG型激光器(输出波长: 1 064 nm, 激光脉冲宽度: 10 ns, 重复频率: 10 Hz)作为激发光源。 其输出的脉冲激光通过反射镜来调整光路, 并通过平凸凹镜(f=100 mm)聚焦于待测样品表面, 烧蚀物质进而诱导激发生成了等离子体。 该等离子体的发射光谱信号由透镜与光纤探头组成的光谱收集系统所采集, 并通过光纤耦合至Avantes公司生产的一台紧凑型6通道光谱仪(仪器型号: AvaSpec-ULS2048-6-USB2, 分辨率: 0.08~0.11 nm, 光谱波长采集范围: 291~1 020 nm)中进行分光探测, 然后传导到耦合器件(CCD)进而实现光电信号的转换, 从而完成对待测样品光谱数据的采集。 实验数据的分析处理在电脑上完成。 其中实验参数如下: 激光能量29 mJ, 重复频率1 Hz, 延时1.3 μ s, 光谱积分时间1.1 ms。

图1 LIBS实验设备图Fig.1 Schematic diagram of LIBS system

1.2 样品

选择10种北方重工生产的特钢作为实验样品, 样品中所含不同物质元素含量都是通过电感耦合等离子体原子发射光谱法和电感耦合等离子体质谱法分析得到的, 其中所有样品中的Fe元素含量都在90%以上, 其余微量元素具体含量如表1所示。 为了减小环境因素干扰和防止样品表面过度烧蚀而导致的探测误差, 将样品固定在3D平台上, 并采用“ 弓” 字形方式不断运动, 进而使得激光脉冲聚焦于平滑样品表面的不同采样点来采集数据。 每组光谱数据是在同一样品表面定点采样10次后光谱的平均值, 每个样品共采集60组光谱数据, 因此10个样品共计采集600组光谱数据。 将每个样品的60组LIBS光谱数据中随机抽取48组数据作为训练集, 剩余12组数据作为测试集。

表1 10种特钢样品的物质元素含量(wt%) Table 1 The contents (wt%) of the constituent element in special steel samples
2 算法介绍
2.1 支持向量机

SVM算法是一种应用广泛的模式识别方法, 也是一种基于统计学习理论的二分类算法[6, 20]。 它可以将输入的原始数据映射到高维空间的某一点上, 由于不同种类的输入样本数据在高维空间中所聚集的点的位置不同, 从而可以通过寻找合适的超平面来实现不同种类输入数据的分类识别。 因此, 当新的数据被映射到相同的高维空间时, 可根据它们映射的点的位置来预测它们属于哪个类别。 SVM可通过构建多个子分类器来实现光谱数据的多分类问题, 在解决小样本及数据非线性等问题上具有很强的适应能力。 然而, 如果根据经验选择参数, 会导致分类结果不理想。 模型训练时设置的惩戒因子C和核参数g都会直接影响对最优分类超平面的求解, 如惩戒因子C过小会导致训练误差变大, 使得模型易陷入欠学习状态; 惩戒因子C过大会导致模型对未知数据的分类预测能力降低, 使得模型易陷入过学习状态; 特别是根据输入数据的不同, 核参数g的大小会影响模型训练与预测的速度。 因此, 为了避免模型发生欠学习或过学习的问题, 以及提高分类模型的建模效率, 需要对C, g进行参数优化。

2.2 粒子群优化算法

粒子群优化算法(particle swarm optimization, PSO)是一种基于群体智能的优化算法, 它模拟了自然界中的生物群体如鸟类或鱼群捕食行为, 通过生物的集体合作来使群体达到最优目标[21]。 该算法的第一个优势是不用导数计算, 进而可以大幅度降低运行时的计算复杂度和计算成本。 另一个优势在于该算法的指向性, 即它可以根据之前的经验, 用新的起点选择下一次迭代的方向。 针对所求问题的最优解, PSO算法首先是在一个有解空间内随机初始化一群粒子, 其中每个粒子的位置都是一个解, 粒子会依据其特有的速度来改变在空间中的位置。 优化过程就是随着粒子的逐代运动, 逐次计算模型的精度值, 通过对应的精度值来评价参数优化的效果好坏, 并在每次迭代中根据个体和全局的最优解更新粒子的位置和速度, 进而朝着整个种群搜索得到的精度值最优位置移动, 以此来达到参数寻优的目的。 每个粒子速度和位置的更新公式如式(1)— 式(3)

Vid(k+1)=ω(k)·Vid(k)+C1·rand(·)[Pid(k)-Xid(k+1)]+C2·rand(·)[Pgd(k)-Xgd(k+1)](1)

Xid(k+1)=Xid(k)+Vid(k+1)(2)

ω(k)=ωstart-k(ωstart-ωend)/kmax(3)

其中, i为第i个粒子; Pid(k)与Pgd(k)分别为个体粒子和种群全局最优解的位置; ω (k)为线性递减惯性系数; rand(· )是[0, 1]之间的随机数; C1和C2是加速因子。 为了优化SVM分类模型的精度和建模效率, 本实验采用PSO算法对惩罚因子C与核参数g进行优化, 其PSO算法参数设置为: 粒子数目为20, 粒子群的最大迭代数为200, 加速因子C1=1.5和C2=1.7, 惯性权重因子ω start和ω end分别为0.9与0.4, 惩罚参数C与核参数g的搜索范围都为(2-8, 28)。

3 结果与讨论
3.1 特征谱线选择

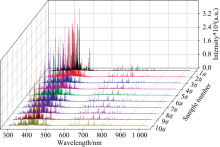
10种特钢样品的典型LIBS光谱如图2所示, 受基体元素Fe的影响, 微量元素的特征谱线强度均较小, 所有样品的谱图都具有极高的相似性。 Fe作为钢铁中主量元素, 当样品被激发后, Fe元素谱线强度通常非常高甚至偏饱和, 与其他微量元素相比量级相差巨大, 由于受基体效应的影响, 高强度Fe线波动范围也比较大, 因此以Fe的特征谱线作为分类模型的输入变量, 人工难以将每个钢铁样品准确区分。 并且一组包含全谱波长的LIBS光谱数据共包含11 022个数据点, 其数据包含如背景噪声, 元素特征谱线之间的相互干扰等大量冗余信息。 若是直接将全谱数据作为输入, 会严重影响分类模型的建模效率以及识别准确率。 为了满足工业现场快速精确检测的需求, 本文以样品所含的微量元素以及美国NIST原子光谱数据库为依据, 筛选出无明显自吸收, 干扰小, 信噪比高的17条特征谱线的峰值强度作为输入变量, 选取的特征谱线如表2所示。

图2 10种钢铁样品的典型LIBS光谱Fig.2 The representative LIBS spectra of 10 different special steels

表2 分析的特征谱线 Table 2 The spectra lines for analysis
3.2 PCA降维提取主成分信息

人工选择特征谱线作输入变量需要依靠实验员的先验经验, 然而这可能会导致选取输入变量时遗漏了某些比较重要的关键信息。 为了减少原始输入数据的高维变量以及提高模型的学习建模效率, 主成分分析法PCA是一种有效的便利的方法。 PCA是一种可以将高维数据利用正交变换快速地转化为包含尽可能多的有效信息的主成分(principal components, PCs) 的方法, 该方法可有效实现数据的压缩降维[22]。 为了提高建模效率, 本实验对全谱数据进行主成分分析进而提取特征信息, 其计算步骤如下: (1) 将训练集中的所有全谱数据作为输入变量, 构造出一个480× 11 022矩阵X, 并对其进行标准化处理, 使所有数值在-1~1之间; (2) 计算矩阵X的特征值和特征向量; (3)由于特征值的大小代表对应特征向量的贡献率大小, 把特征值按序排列, 并计算不同特征向量即主成分, 对整体的累计贡献率。 如图3所示, 可知前10个主成分对整体的贡献率超过99.9%。 由图4训练集前3个主成分的三维得分图可知, 光谱数据经PCA算法降维提取主成分后仍难以区分, 需要进一步的优化。 因此, 本实验将累计贡献率达98.27%的前17个主成分与表2中所选取的特征谱线分别作为分类模型的输入变量, 研究SVM模型使用这两种不同输入变量对相似钢铁样品的识别效果。 其中主成分个数选17个是为了与人工选择的17条特征谱线的数量保持一致, 避免数据维度的大小差异对模型造成影响, 进而体现PCA降维性能的准确性。

图3 前50个主成分对原始数据的贡献率Fig.3 The cumulative contribution of the first 50 PCs to the original data

图4 10个钢铁样品的主成分三维得分图Fig.4 Score of first 3 PCs of 10 steel sample

3.3 四种分类模型识别结果对比

分别以17条特征谱线和经PCA对全谱数据降维提取的主成分, 来作为SVM分类模型的输入变量进行对比实验, 并用网格寻优和PSO两种不同的方法对模型参数C, g进行优化, 优化结果如图5和表3所示。 由图5可看出, PSO-SVM以及PSO-PCA-SVM模型能经较少的迭代训练后得到较好的参数(C, g), 尤其是PSO-PCA-SVM模型在第3次迭代计算时, 仅花费7.45 s就计算出最优参数(C, g)为(14.141, 2.4357), 训练集的识别精度为98.125%。 并且在后续的迭代训练中无提升或提升较小。

图5 (a): PSO-SVM的参数优化结果; (b): PSO-PCA-SVM的参数优化结果; (c): SVM的参数优化结果; (d): PCA-SVM的参数优化结果Fig.5 The parameter optimization of (a): PSO-SVM; (b): PSO-PCA-SVM; (c): SVM and (d): PCA-SVM

表3 不同分类模型的优化结果 Table 3 The optimized classification results of different methods

由表3可知PCA-SVM在训练集、 测试集的识别精度最高, 然而其优化时间257.84 s是所有方法中最长的。 而PSO-SVM, PSO-PCA-SVM与SVM相比, 三者的识别精度几乎无差别, 在前200次迭代训练的过程中, PSO-SVM, PSO-PCA-SVM模型分别在第137次, 第3次迭代中达到最高准确率, 其优化时间分别为136.18和7.45 s。 然而, PSO优化的模型可在很少的迭代次数下达到一个较高的准确率, 该准确率基本可达97%以上, 并且后续继续增加训练的迭代次数对准确率无明显提升。 该实验结果说明使用PSO优化的SVM分类模型, 可在设置较小的迭代次数如10次情况下, 极大地减小优化时间。 PSO-SVM与PSO-PCA-SVM模型的参数优化时间分别仅需11.5与17.35 s, 这明显比网格寻优的参数优化方法要快。

采用网格寻优法来优化参数的PCA-SVM与SVM模型的计算时间分别为130.78与115.64 s。 该结果表明PSO方法相比于网格寻优方法能显著提高SVM分类模型的建模效率。

4 结论

通过LIBS技术实现了对10种特钢样品的快速检测分类, 为了探寻效率较高的优化方法, 采用人工选取谱线、 PCA、 网格寻优与PSO等不同方法分别来优化输入变量和SVM模型的参数, 建立了PSO-SVM、 PSO-PCA-SVM、 PCA-SVM和SVM四种分类模型。 实验结果表明, PSO-SVM, PSO-PCA-SVM, PCA-SVM与SVM对钢铁样品测试集的平均识别精度分别为96.67%, 95.83%, 97.5%, 96.67%; 四种模型的优化时间分别为11.5, 144.41, 257.84与115.64 s。 从中可看出PCA-SVM的精度最高, 但是训练时间最长; 而PSO-SVM相比于单纯的SVM不仅提高了识别精度, 还大幅降低了建模时间, 最低可至11.5 s。 实验结果还表明, PCA提取的特征信息作输入可以提高分类精度, 但需要一定的计算时间; 而PSO-SVM对测试集的平均最高精度是96.67%, 该结果仅次于PCA-SVM的97.5%, 然而计算时间却几乎仅为PCA-SVM算法的二十分之一。 这说明PSO-SVM算法有助于缩短计算时间, 为实现快速准确的钢铁分类提供一种新的途径。

参考文献
[1] Afgan M S, Hou Z, Wang Z. Journal of Analytical Atomic Spectrometry, 2017, 32(10): 1905. [本文引用:1]
[2] Almessiere M A, Altuwiriqi R, Gondal M A, et al. Talanta, 2018, 185: 61. [本文引用:1]
[3] Wang Z, Deguchi Y, Shiou F, et al. ISIJ International, 2016, 56(5): 723. [本文引用:1]
[4] Li X, Zhang L, Tian Z, et al. Journal of Analytical Atomic Spectrometry, 2020, 35: 2928. [本文引用:2]
[5] Zeng Q D, Deng F, Zhu Z H, et al. Plasma Sci. Technol, 2019, 21(3): 034006. [本文引用:1]
[6] Zhang D C, Ding J, Feng Z Q, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2021, 180, 106192. [本文引用:2]
[7] Yue Z Q, Sun C, Chen F Y, et al. Biomedical Optics Express, 2021, 12(5): 2559. [本文引用:1]
[8] Zeng Q D, Guo L B, Li X Y, et al. Journal of Analytical Atomic Spectrometry, 2016, 31(3): 767. [本文引用:1]
[9] Gazeli O, Bellou E, Stefas D, et al. Food Chemistry, 2020, 302: 125329. [本文引用:1]
[10] Yelameli M, Thornton B, Takahashi T, et al. Journal of Chemometrics, 2019, 33(2): e3092. [本文引用:1]
[11] Yao M, Fu G, Chen T, et al. Journal of Analytical Atomic Spectrometry, 2021, 36: 361. [本文引用:1]
[12] Shin S, Moon Y, Lee J, et al. Plasma Science and Technology, 2019, 21(3): 034011. [本文引用:1]
[13] Kim E, Kim Y, Srivastava E, et al. Chemometrics and Intelligent Laboratory Systems, 2020, 203(1): 104072. [本文引用:1]
[14] Chen G H, Zeng Q D, Li W X, et al. Optics Express, 2022, 30(6): 9428. [本文引用:1]
[15] Wang J M, Liao X Y, Zheng P C, et al. Analytical Letters, 2018, 51(4): 575. [本文引用:1]
[16] Wang J M, Zheng P C, Liu H D, et al. Analytical Methods, 2016, 8(15): 3204. [本文引用:1]
[17] Liu Y Y, Zhao S Y, Gao X, et al. RSC Advances, 2022, 12(53): 34520. [本文引用:1]
[18] LI Ming-liang, DAI Yu-jia, QIN Shuang, et al(李明亮, 戴宇佳, 秦爽, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(2): 587. [本文引用:1]
[19] ZHAO Shang-yong, ZHOU Zhi-ming, SONG Chao, et al(赵上勇, 周志明, 宋超, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(8): 2629. [本文引用:1]
[20] Cortes C, Vapnik V, et al. Mach. Learn. , 1995, 20(3): 273. [本文引用:1]
[21] Marini F, Walczak B. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 153. [本文引用:1]
[22] Porizka P, Klus J, Kepes, E, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2018, 148: 65. [本文引用:1]